|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A verseny időtartama 90 perc. A feladatok pontozása: minden helyes válasz 5 pontot ér; helytelen válaszra 0 pont, válasz nélkül hagyott kérdésekre 1-1 pontot jár.
1. Juli kiszámolta 2015-nek a 2016-nál kisebb természetes szám kitevőjű hatványait, majd összeadta a kapott számokat. Melyik az összeg legkisebb helyiértékén álló számjegy?
(A) 0; (B) 1; (C) 2; (D) 5; (E) 6.
2. Egy statisztikai minta elemei 7; 2; 14; 21; 191 és 41. Egy új adat hozzávételével a minta terjedelme 15-tel nő. Melyik lehet az új adat?
(A) ; (B) ; (C) ; (D) 205; (E) 208.
3. Hány olyan 2015-jegyű szám van, amelyre teljesül, hogy bármely két számjegyének a szorzata ugyanannyi? (A) 0; (B) 9; (C) 12; (D) 18; (E) 2015.
4. Mennyi a tört értéke? (A) ; (B) ; (C) ; (D) ; (E) 1.
5. Hány valós megoldása van az egyenletnek?
(A) 0; (B) 1; (C) 2; (D) 4; (E) 7.
6. Hány olyan számrendszer van, amelyben a 441 alakú szám négyzetszám, és amelynek alapszámára teljesül, hogy ? (A) 5; (B) 6; (C) 7; (D) 8; (E) 9.
7. Hány elemű halmaz a egyenlet értelmezési tartománya? (A) 0; (B) 1; (C) 2; (D) 2015; (E) végtelen sok.
8. Az ábrán látható összeadásban minden betű egy számjegyet jelöl és . Hány különböző háromjegyű számot jelölhet a SOR szó, ha az azonos betűk azonos számokat jelölnek?
(A) 200; (B) 216; (C) 243; (D) 270; (E) 300.
9. Évit teniszedzés után minden alkalommal édesapja viszi haza autóval, aki pontosan az edzés végére érkezik meg. Egyik nap az edzés hamarabb ért véget, és Évi az edzés után azonnal elindult gyalog haza a szokott útvonalon. Negyed óra múlva találkozott az autóval érkező édesapjával. Azonnal beszállt az autóba, és így a megszokottnál 10 perccel korábban ért haza. Hány perccel hamarabb ért véget a szokásosnál az edzés, ha minden más a megszokott időpontban és tempóban zajlott, és az autó megfordulásához, valamint a beszálláshoz szükséges időtartamtól eltekintünk?
(A) 10; (B) 15; (C) 20; (D) 25; (E) 30.
10. Hány megoldása van az egész számok halmazán az egyenletnek? (A) 0; (B) 1; (C) 2; (D) 3; (E) végtelen sok.
11. Hány fok abban a háromszögben a két kisebb belső szög nagyságának a különbsége, amelynek a leghosszabb oldala 10 cm, és két magasságára is igaz, hogy a hossza legalább akkora, mint a hozzá tartozó alap hossza?
(A) 0; (B) 10; (C) 20; (D) 30; (E) 45.
12. Mennyi az egyenlet gyökeinek a szorzata?
(A) ; (B) 0; (C) 2015; (D) 8060; (E) 18 135.
13. Sárkányföldön ötfejű, hatfejű és hétfejű sárkányok élnek. A hatfejűek mindig hazudnak, az ötfejűek és a hétfejűek mindig igazat mondanak. Egyszer négy sárkány találkozott. Tűztorok azt állította, hogy négyüknek összesen 24, Parázsorr azt, hogy 23, Füstfül azt, hogy 22, Lángnyelv pedig azt, hogy 21 fejük van. Hogy hívják az igazmondó sárkányt?
(A) Tűztorok; (B) Parázsorr; (C) Füstfül; (D) Lángnyelv; (E) Ezekből az adatokból nem lehet meghatározni.
14. Hány olyan alakú háromjegyű szám van, melyre a tört természetes szám? (A) 6; (B) 7; (C) 9; (D) 10; (E) 12.
15. Mi az értékkészlete a valós számok halmazán értelmezett valós értékű függvénynek (a a szám egészrészét jelöli)?
(A) ; (B) ; (C) ; (D) ; (E) .
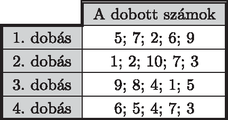
16. Öt érme oldalaira felírtuk az 1; 2; 3; 4; 5; 6; 7; 8; 9 és 10 számokat úgy, hogy minden érme minden oldalára egy szám került. Peti ötször egymás után feldobta az öt érmét, és leírta az első négy dobás után az öt érmén látható öt számot (lásd táblázat). Megállapította, hogy az ötödik dobás után az öt érmén látható számok összege a lehető legkisebb lett. Mennyi volt az ötödik dobás után az öt érmén látható számok összege? (A) 15; (B) 16; (C) 17; (D) 18; (E) 19.
17. Legyen az összeg, ahol 25-nél kisebb pozitív egész szám. Kiválasztunk két tetszőleges összeget. Mennyi annak a valószínűsége, hogy a kiválasztott két összeg egyike prímszám?
(A) ; (B) ; (C) ; (D) ; (E) .
18. Egy -ös négyzetrács 13 négyzetére egy-egy fekete korongot helyeztünk (lásd ábra). A korongokat lépésekkel mozgatjuk a táblán. Egy lépés abból áll, hogy először kiválasztunk egy sorból vagy egy oszlopból három egymás melletti olyan négyzetet, hogy csak a középső és egyik szélső négyzeten legyen korong, ezután pedig a szélső négyzeten lévő korongot áthelyezzük a másik szélső négyzetre. Legkevesebb hány lépésben érhető el, hogy minden korong kezdetben üres négyzetre kerüljön át?
(A) 15; (B) 24; (C) 27; (D) 30; (E) Az átrendezés nem valósítható meg.
19. Egy szobában 10 szék van egy sorban egymás mellett. A székek kezdetben üresek. Időnként valaki leül egy üres székre, és ugyanakkor az egyik szomszédja, ha van, feláll. Hány ember ülhet egyszerre a székeken, ha az emberek száma a lehető legnagyobb?
(A) 5; (B) 7; (C) 8; (D) 9; (E) 10.
20. Hány fok annak a háromszögnek a legnagyobb szöge, amelynek a területe , ahol és a háromszög két oldalának hossza?
(A) 60; (B) 75; (C) 90; (D) 105; (E) 120.
21. Melyik kifejezéssel egyenlő a összeg, ha ?
(A) ; (B) ; (C) ; (D) ; (E) .
22. Legyen az a függvény, amely minden valós -hez a számegyenes -et jelölő pontjának a intervallum attól legtávolabb lévő, egész számot jelölő pontjától való távolságát rendeli. Mi ennek az függvénynek a hozzárendelési szabálya?
(A) ; (B) ; (C) ;
(D) ; (E) .
23. Hány olyan természetes szám van, melyre az polinom helyettesítési értéke négyzetszám?
(A) 0; (B) 1; (C) 2; (D) 5; (E) végtelen sok.
24. Az háromszög csúcsból induló magasságának hossza harmonikus közepe azon két szakasz hosszának, amelyekre a magasság a oldalt bontja. Mennyi a összeg, ha a háromszögnek a , a csúcsnál lévő belső szöge?
(A) 1; (B) ; (C) 2; (D) (E) 3.
25. Hány olyan rendezett számhármas van, melyre , ha ? (A) 0; (B) 1; (C) 2; (D) 3; (E) 4.
26. Mennyi a tört lehető legnagyobb értéke?
(A) ; (B) ; (C) ; (D) ; (E) 2.
27. Egységnyi élű fehér kockákból egységnyi élű kockát állítunk össze (), majd a kapott kocka lapjait pirosra festjük. Hány olyan egységnyi élű kocka lesz, amelynek van olyan, vele lappal érintkező szomszédja, amelynek nála 1-gyel több piros lapja van?
(A) ; (B) ; (C) ; (D) ; (E) .
28. A és pontok egy átmérőjű félkörív pontjai. Az pont az sugár egy olyan pontja, amelyre . Hány fok a nagysága, ha ? (A) 10; (B) 15; (C) 20; (D) 25; (E) 30.
29. Ernő ötöslottó szelvényeket töltött ki. Minden lehetséges számötöst pontosan egy szelvényen jelölt be. Hány olyan szelvény van ezek között, melyben a bejelölt öt szám közül legalább három szomszédos? (Az ötöslottó szelvényeken az első 90 pozitív egész számból kell ötöt bejelölni.)
(A) ; (B) ; (C) ; (D) ; (E) .
30. Legyen az egyenlő szárú derékszögű háromszög átfogójának olyan pontja, melyre . Hány fok a nagysága, ha létezik derékszögű háromszög, amelynek oldalai , és ? (A) 20; (B) 25; (C) 30; (D) 35; (E) 40.
A középiskolás tanárverseny eredménye
1. Koncz Levente (Budapest, Óbudai Árpád Gimn.) ..... 140 pont
2. Fridrik Richárd (Szegedi Tudományegyetem) ..... 136 pont
3. Fonyóné Németh Ildikó (Keszthelyi Vajda János Gimn.) ..... 115 pont
3. Fonyó Lajos (Keszthelyi Vajda János Gimn.) ..... 115 pont
5. Szaszkó-Bogárné Eckert Bernadett (Szegedi Radnóti Miklós Kís. Gimn.) ..... 113 pont
6. Baloghné Cseh Judit (Szolnoki Varga Katalin Gimn.) ..... 112 pont
7. Cs. Nagy András (Váci Boronkay György Szakközépiskola) ..... 105 pont
8. Merényi Imre (Váci Boronkay György Szakközépiskola) ..... 104 pont
9. Czinki József (Budapest, Óbudai Árpád Gimn.) ..... 103 pont
10. Tigyi István (Szegedi Radnóti Miklós Kísérleti Gimn.) ..... 101 pont.
Az általános iskolás tanárverseny eredménye
1. Csordás Péter (Kecskeméti Katona József Gimn.) ..... 136 pont
1. Nagy Tibor (Kecskeméti Református Ált. Isk.) ..... 136 pont
3. B. Varga József (Temerini Petar Kocsity Ált. Isk.) ..... 125 pont
4. Tóth Gabriella (Palicsi Miroslav Antic Ált. Isk.) ..... 111 pont
5. Egyed László (Bajai III. Béla Gimn.) ..... 109 pont
6. Csordás Mihály (Kecskeméti Mategye Alapítvány) ..... 105 pont.
Az általános iskolás tanárverseny feladatait nem közöljük. |
 PDF | MathML
PDF | MathML