Az Eötvös Loránd Fizikai Társulat 2016. évi Eötvös-versenye október 14-én délután 3 órai kezdettel tizennégy magyarországi helyszínen¹ került megrendezésre. Ezért külön köszönettel tartozunk mindazoknak, akik ebben szervezéssel, felügyelettel a segítségünkre voltak. A versenyen a három feladat megoldására 300 perc áll rendelkezésre, bármely írott vagy nyomtatott segédeszköz használható, de zsebszámológépen kívül minden elektronikus eszköz használata tilos. Az Eötvös-versenyen azok vehetnek részt, akik vagy középiskolai tanulók, vagy a verseny évében fejezték be középiskolai tanulmányaikat. Összesen 77 versenyző adott be dolgozatot, 18 egyetemista és 59 középiskolás.
Ismertetjük a feladatokat és azok megoldását.

 

Megoldás. Ha a rajztábla és a pénzérme között a súrlódási tényező elegendően nagy lenne ($\mu >R{\omega }^2/g$), akkor a pénzérme nem csúszna meg, hanem a táblához tapadva követné annak mozgását. A feladat szövege szerint nem ez a helyzet, így a rajztábla indításakor a pénzérme azonnal megcsúszik. Sejthető, hogy néhány periódusidőnyi átmeneti (tranziens) szakasz után az érme mozgása állandósul. Megmutatjuk, hogy az egyenletes körmozgást végző pénzérme kielégíti a Newton-féle mozgásegyenletet.
Az $m$ tömegű pénzérmére vízszintes irányban egyetlen erő hat: a $\mu mg$ nagyságú, de állandóan változó irányú csúszási súrlódási erő. Stacionárius körmozgás esetén az érme sebességének nagysága állandó, ezért a súrlódási erő mindig merőleges a sebességvektorra. A pénzérme körmozgásának szögsebessége nem lehet más, mint a rajztábla mozgásának $\omega$ körfrekvenciája. A körpálya $r$ sugarát a mozgásegyenletből határozhatjuk meg:

$\begin{array}{c}{\displaystyle \mu mg=mr{\omega }^2\mathrm{,}\text{<span style="font-weight: normal;font-style: normal;">ebből</span>}r=\frac{\mu g}{{\omega }^2}\mathrm{.}}\end{array}$

(1)

Érdekes, hogy $r$ nem függ a rajztábla pályájának $R$ sugarától.

 

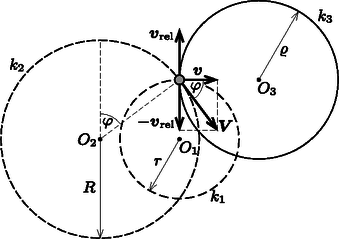1. ábra

 

Most térjünk rá arra a kérdésre, hogy milyen nyomot hagy az érme a rajztáblán! Ehhez a két test relatív mozgását kell elemezni. Az 1. ábrán látható $r$ sugarú $k_1$ kör a pénzérme pályáját mutatja az álló vonatkoztatási rendszerben, az $R$ sugarú $k_2$ kör a rajztábla éppen az érmével érintkező pontjának későbbi pályáját jelzi, végül pedig a $\varrho$ sugarú $k_3$ kör a táblán hagyott grafitnyomnak felel meg. Az érmére ható csúszási súrlódási erő az $O_1$ pont felé mutat, ezzel ellentétes tehát az érme rajztáblához viszonyított ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}}_{\text{<span style="font-weight: normal;font-style: normal;">rel</span>}}$ sebessége. Az érme álló vonatkoztatási rendszerhez viszonyított $\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}$ sebessége viszont erre merőleges, így a rajztábla érmével éppen érintkező pontjának $\text{<span style="font-weight: bold;"><span style="font-style: italic;">V</span></span>}=\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}-{\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}}_{\text{<span style="font-weight: normal;font-style: normal;">rel</span>}}$ sebességére fennáll a Pitagorasz-tétel:

$\begin{array}{c}{\displaystyle {\text{<span style="font-weight: bold;"><span style="font-style: italic;">V</span></span>}}^2={\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}}^2+{\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}}_{\text{<span style="font-weight: normal;font-style: normal;">rel</span>}}^2\mathrm{.}}\end{array}$

(2)

Mivel az állandósult mozgásszakaszban mindhárom sebességvektor $\omega$ szögsebességgel forog az időben, a nagyságukat kifejezhetjük a körpályák sugarával:

$\begin{array}{c}{\displaystyle |\text{<span style="font-weight: bold;"><span style="font-style: italic;">V</span></span>}|=R\omega \mathrm{,}|\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}|=r\omega \mathrm{,}|{\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}}_{\text{<span style="font-weight: normal;font-style: normal;">rel</span>}}|=\varrho \omega \mathrm{,}}\end{array}$

amelyeket a $\left(2\right)$ egyenletbe írva a sugarak között kapunk összefüggést:

$\begin{array}{c}{\displaystyle R^2=r^2+{\varrho }^2\mathrm{.}}\end{array}$

Ezt és az $\left(1\right)$ eredményt felhasználva megkapjuk a pénzérme által a rajztáblán hagyott kör alakú grafitnyomok $\varrho$ sugarát:

$\begin{array}{c}{\displaystyle \varrho =\sqrt[]{R^2-{\left(\frac{\mu g}{{\omega }^2}\right)}^2}\mathrm{.}}\end{array}$

Az érme megcsúszásának $\mu <R{\omega }^2/g$ feltétele miatt ez mindig valós.

 

Megjegyzés. Az ábráról leolvasható, hogy az érme mozgása nincs szinkronban a rajztábla mozgásával, hanem ahhoz képest folyamatosan ,,késik''. A fáziskésés $\phi$ szögét is a sebességvektorok által kifeszített derékszögű háromszög segítségével határozhatjuk meg:

$\begin{array}{c}{\displaystyle \text{cos}\phi =\frac{|\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}|}{|\text{<span style="font-weight: bold;"><span style="font-style: italic;">V</span></span>}|}=\frac{r}{R}=\frac{\mu g}{R{\omega }^2}\mathrm{,}}\end{array}$

amely csúszó érme esetén biztosan kisebb $1$-nél.

 

2. feladat. Két egyforma, fekete lapon kilenc-kilenc kicsi fehér pötty van. A szomszédos pöttyök középpontjának távolsága $5\mathrm{,}8\text{mm}$. A lapokról egy fényképezőgéppel képet készítettünk: a fényképezőgép a távolabbi, a lencsétől $25\text{cm}$ távolságra lévő lapról éles képet adott, a közelebbiről viszont elmosódott a kép (2. ábra). A bal oldali ábrán a teljes kép látható, a jobb oldali ábrán pedig a kép tetejének kinagyított részlete. A fényképezőgép lencséjének fókusztávolsága $18\text{mm}$.

 

2. ábra

 

Becsüljük meg a megadott és a képekről lemért adatokból a közelebbi lap távolságát a lencsétől, valamint a fényképezőgép lencséjének átmérőjét!

(Tichy Géza, Vankó Péter)

 

Megoldás. A feladat megoldásának lényege, hogy megértsük, miért lesz a közelebbi tárgy képe elmosódott. A 3. ábrán két pontszerű tárgy képe látható. A távolabbiról a lencse pontosan a CCD érzékelő síkjában hoz létre éles, pontszerű képet. A közelebbiről viszont távolabb keletkezne éles kép, így a CCD-n egy elmosódott, $\delta$ átmérőjű folt keletkezik. Az ábráról leolvasható, hogy

$\begin{array}{c}{\displaystyle \frac{D}{\delta }=\frac{k}{k-k_0}\mathrm{,}}\end{array}$

a leképzési törvény alapján pedig:

$\begin{array}{c}{\displaystyle \frac{1}{t_0}+\frac{1}{k_0}=\frac{1}{f}\text{és}\frac{1}{t}+\frac{1}{k}=\frac{1}{f}\mathrm{.}}\end{array}$

 

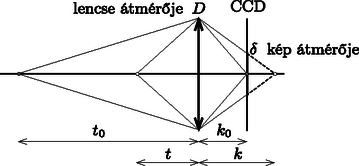3. ábra

 

A 4. ábra alapján a közelebbi tárgy távolsága a két kép nagyításának arányából határozható meg: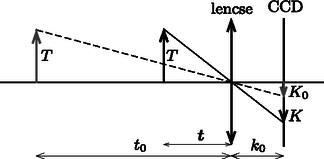

${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{K_0}{T}}& {\displaystyle =\frac{k_0}{t_0}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{K}{T}}& {\displaystyle =\frac{k_0}{t}\mathrm{,}}\hfill \\ \hfill {\displaystyle \lambda }& {\displaystyle =\frac{K}{K_0}=\frac{t_0}{t}\mathrm{.}}\hfill \end{array}}$

A 2. ábra bal oldali részéről leolvasható a szélső pöttyök középpontjának távolsága (a szomszédos pöttyök távolságának kétszerese) mindkét képen (5. ábra).

 

4. ábra

 

 

5. ábra

 

Ebből:

${\displaystyle \begin{array}{cc}\hfill {\displaystyle \lambda }& {\displaystyle =\frac{K}{K_0}=\frac{2b}{2a}=\frac{33\text{mm}}{7\mathrm{,}6\text{mm}}=4\mathrm{,}\mathrm{34,}}\hfill \\ \hfill {\displaystyle t}& {\displaystyle =\frac{t_0}{\lambda }=\frac{25\text{cm}}{4\mathrm{,}34}=5\mathrm{,}8\text{cm}\mathrm{.}}\hfill \end{array}}$

A 2. ábra jobb oldali (nagyított) részén leolvasható a pöttyök átmérőjének és távolságának aránya (6. ábra). Ebből:

$\begin{array}{c}{\displaystyle \varrho =\frac{c\text{'}}{a\text{'}}=2\frac{c\text{'}}{2a\text{'}}=2\cdot \frac{5\mathrm{,}8\text{mm}}{24\text{mm}}=0\mathrm{,}48.}\end{array}$

 

6. ábra

 

Ez alapján kiszámíthatjuk, hogy mekkora lenne a 2. ábra bal oldali felén a közelebbi pöttyök átmérője, ha nem lenne elmosódva (7. ábra):

$\begin{array}{c}{\displaystyle d=\varrho b=\varrho \frac{2b}{2}=0\mathrm{,}48\cdot \frac{33\text{mm}}{2}=8\mathrm{,}0\text{mm}\mathrm{.}}\end{array}$

Ugyanitt leolvasható az elmosódott kép átmérője is: $d\text{'}\text{'}=15\mathrm{,}5\text{mm}$. A két átmérő különbsége a kép elmosódottsága (ekkora lenne egy pontszerű tárgy elmosódott képe ezen a képen):

$\begin{array}{c}{\displaystyle e=d\text{'}\text{'}-d=7\mathrm{,}5\text{mm}\mathrm{.}}\end{array}$

 

7. ábra

 

Ezután már csak néhány számítás van hátra. A 3. ábrán jelölt képtávolságok:

${\displaystyle \begin{array}{cc}\hfill {\displaystyle k_0}& {\displaystyle =\frac{t_{0}f}{t_0-f}=19\mathrm{,}4\text{mm}\mathrm{,}}\hfill \\ \hfill {\displaystyle k}& {\displaystyle =\frac{tf}{t-f}=26\mathrm{,}2\text{mm}\mathrm{.}}\hfill \end{array}}$

Két pötty távolsága a fényképezőgép CCD érzékelőjén (ez a távolság a valóságban $a_0=5\mathrm{,}8\text{mm}$, meg van adva):

$\begin{array}{c}{\displaystyle a_{\text{CCD}}=\frac{k_0}{t_0}{a}_0=\frac{19\mathrm{,}4\text{mm}}{250\text{mm}}\cdot 5\mathrm{,}8\text{mm}=0\mathrm{,}45\text{mm}\mathrm{,}}\end{array}$

amiből a 2. ábra bal oldali képének nagyítása a CCD-n kialakuló képhez viszonyítva:

$\begin{array}{c}{\displaystyle N=\frac{a}{a_{\text{CCD}}}=\frac{2a}{2a_{\text{CCD}}}=\frac{7\mathrm{,}6\text{mm}}{2\cdot 0\mathrm{,}45\text{mm}}=8\mathrm{,}4.}\end{array}$

Ebből az elmosódottság a CCD érzékelőn:

$\begin{array}{c}{\displaystyle \delta =\frac{e}{N}=\frac{7\mathrm{,}5\text{mm}}{8\mathrm{,}4}=0\mathrm{,}9\text{mm}\mathrm{,}}\end{array}$

amiből viszont a keresett lencseátmérő a 3. ábra alapján:

$\begin{array}{c}{\displaystyle D=\delta \frac{k}{k-k_0}\approx 3\mathrm{,}5\text{mm}\mathrm{.}}\end{array}$

 

Megjegyzések. 1. A kérdezett mennyiségek hibájára csak becslést adunk. A lehető legpontosabb (tized mm-es) leolvasás és egy kicsit ,,nagyvonalúbb'' (fél mm pontos) leolvasás adataival is végigszámolva azt kapjuk, hogy a közelebbi tárgy távolságára kapott eredmény hibája 1‐2%, a lencse átmérő hibája pedig 10‐15%.
2. A közelebbi tárgy távolságát azért kérdeztük, hogy segítsük a gondolatmenetet. Ezt több versenyző is meghatározta, de nem tudtak továbblépni. Egyetlen helyes megoldón kívül szinte senki nem tudta helyesen értelmezni a kép elmosódottságát; néhányan a fény elhajlásával próbálták megmagyarázni, ami szintén helytelen.

 

3. feladat. Egy $r$ sugarú, $d$ vastagságú $\left(d\ll r\right)$, $\varrho$ fajlagos ellenállású fémkorong $A$ pontjába $I$ erősségű áramot vezetünk, $B$ pontjából pedig elvezetjük azt.
Mekkora feszültség mérhető a 8. ábrán látható $C$ és $D$ pontok között?

(Vigh Máté)

 

8. ábra

 

 

Megoldás. A fémkorong vizsgálata előtt érdemes egy végtelen fémlemez esetéből kiindulni. Képzeljük el, hogy egy végtelen fémlap $A$ pontjába $2I$ áramot vezetünk, a $B$ pontból pedig elvezetjük azt. Ha csak az $A$ jelű elektróda lenne jelen, a fémlemezben a bevezetett áram izotrop módon terjedne szét, így az $A$ ponttól $r_1$ távolságra az áramsűrűség nagysága

$\begin{array}{c}{\displaystyle j_1=\frac{2I}{2\pi r_{1}d}}\end{array}$

lenne. A differenciális Ohm-törvény értelmében ezt az áramsűrűséget a lemezben megjelenő $E_1=\varrho j_1$ térerősségű elektromos mező tartja fenn, így az $A$ elektróda hatására a végtelen fémlemezben az $r_1$ távolsággal fordítottan arányos erősségű, az $A$ ponttal ellentétes irányba mutató, ,,sugaras'' elektromos mező alakul ki. Hasonlóan, ha csak a $B$ jelű csatlakozó lenne jelen, akkor $r_2$ távolságban $E_2=2\varrho I/\left(2\pi r_{2}d\right)$ térerősségű, a $B$ pont felé mutató elektromos tér jönne létre. Mivel mindkét elektróda jelen van, így a lemezben kialakuló elektromos tér (és áramsűrűség) az előbbi két eset szuperpozíciójaként (vektori összegeként) számolható.
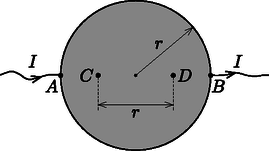Tekintsük most a végtelen fémlemez tetszőleges $P$ pontját (lásd a 9. ábrát)! Itt az $A$ és $B$ elektródák hatására külön-külön ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_1$ és ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_2$ térerősség alakul ki, melyek nagyságára az eddigiek szerint fennáll az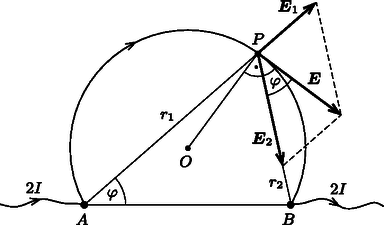

$\begin{array}{c}{\displaystyle \frac{|{\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_1|}{|{\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_2|}=\frac{r_2}{r_1}}\end{array}$

egyenlőség. Ebből és a váltószögek egyenlőségéből látszik, hogy az $ABP$ háromszög hasonló a térerősségvektorok által meghatározott háromszöghöz, ezért az eredő térerősségvektor a $PB$ szakasszal ugyanakkora szöget zár be, mint a $PAB$ szög. Ez viszont azt jelenti, hogy az $ABP$ háromszög ($O$ középpontú) köréírt körét a $P$ pontbeli eredő térerősség érinti, hiszen van két szögünk ($PAB\sphericalangle$, illetve az $\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}$ és ${\text{<span style="font-weight: bold;"><span style="font-style: italic;">E</span></span>}}_2$ vektorok által bezárt szög), melyek egyenlőségük miatt a kör ugyanazon $PB$ ívéhez tartozó kerületi szögek.

 

9. ábra

 

A fentiekből következik, hogy az eredő térerősségvektor a fémsík tetszőleges pontjában érintője az $A$, $B$ és a kiszemelt pontra illeszkedő körívnek, a lemezben kialakuló elektromos erővonalak (és így az áramvonalak is) tehát körív alakúak, melyek átmennek az $A$ és $B$ pontokon.
Most vágjuk ki gondolatban a végtelen fémlapból a 10. ábrán látható, a feladatnak megfelelő korong alakú részt! A korong pereme mentén az áramok a kivágás előtt is érintő irányban folytak, így az áramokra kirótt határfeltétel automatikusan teljesül. A korong kivágása tehát nem változtatja meg sem a külső, sem a belső árameloszlást, és így a feszültségviszonyokat sem. A végtelen fémlapban az áram be- és kivezetési pontjának közvetlen közelében az árameloszlás izotrop volt (itt a távolabbi elektróda hatása már nem érződik), így a korong kivágása előtt a fémlemezbe vezetett $2I$ erősségű áramnak pontosan a fele jutott be a korongba (lásd a 10. ábra kinagyított részletét). A feladatbeli kérdés tehát egyenértékű azzal, hogy mekkora volt a feszültség a végtelen fémlap $C$ és $D$ pontjai között a korong kivágása előtt.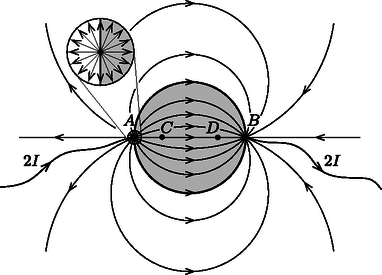

 

10. ábra

 

Az $A$ pontban bevezetett $2I$ áram hatására az elektródától $r$ távolságra a fémlap potenciálja (az $A$ és $B$ pontok között félúton, a korong középpontjában elhelyezkedő referenciaponthoz képest) a térerősség integrálásával kapható meg:

$\begin{array}{c}{\displaystyle \Phi \left(r_1\right)=\underset{r_1}{\overset{r_0}{\int }}{E}_1\left(r\text{'}\right)\text{d}r\text{'}=\frac{2\varrho I}{2\pi d}\underset{r_1}{\overset{r_0}{\int }}\frac{1}{r\text{'}}\text{d}r\text{'}=-\frac{\varrho I}{\pi d}\text{ln}\frac{r_1}{r_0}\mathrm{,}}\end{array}$

ahol $r_0=r$. Ennek felhasználásával az $A$ pontbeli elektróda által a $C$ és $D$ pontok között létrehozott feszültség nagysága

$\begin{array}{c}{\displaystyle U_{CD}^{\left(A\right)}=\frac{\varrho I}{\pi d}\left(-\text{ln}\frac{r}{2r_0}+\text{ln}\frac{3r}{2r_0}\right)=\frac{\varrho I}{\pi d}\text{ln}3.}\end{array}$

Ugyanekkora potenciálkülönbséget hoz létre a $B$ jelű elektróda is, így a szuperpozíció értelmében a $C$ és $D$ pontok között eső feszültség

$\begin{array}{c}{\displaystyle U_{CD}=U_{CD}^{\left(A\right)}+U_{CD}^{\left(B\right)}=2U_{CD}^{\left(A\right)}=\frac{2\varrho I}{\pi d}\text{ln}3.}\end{array}$

Ekkora tehát a kivágott fémkorong $C$ és $D$ pontjai közötti feszültség is.

 

$*$

 

Az ünnepélyes eredményhirdetésre és díjkiosztásra 2016. november 18-án délután került sor az ELTE TTK Konferenciateremben. Meghívást kaptak az 50 és 25 évvel ezelőtti Eötvös-verseny nyertesei is. Jelen volt az 50 évvel ezelőtti győztes Rácz Miklós és a 25 évvel ezelőtti díjazottak közül Gefferth András, Miklós György és Rózsa Balázs. Utóbbi az akkori feladatok ismertetése után röviden beszélt a versennyel kapcsolatos emlékeiről és pályájáról.
Ezután következett a 2016. évi verseny feladatainak és megoldásainak bemutatása. Az 1. és 3. feladat megoldását Tichy Géza, a 2. feladatét Vankó Péter ismertette.
Az esemény végén került sor az eredményhirdetésre. A díjakat Patkós András, az Eötvös Loránd Fizikai Társulat elnöke adta át.
Egyetlen versenyző sem oldotta meg mindhárom feladatot, így a versenybizottság nem adott ki első díjat.
Két feladat helyes megoldásáért második díjat nyert Kovács Péter Tamás, a Zalaegerszegi Zrínyi Miklós Gimnázium 12. osztályos tanulója, Juhász Tibor és Pálovics Róbert tanítványa valamint Tompa Tamás Lajos, a miskolci Földes Ferenc Gimnázium 12. osztályos tanulója, Zámborszky Ferenc és Kovács Benedek tanítványa.
Egy feladat helyes megoldásáért harmadik díjat nyert Forrai Botond, a budapesti Baár-Madas Református Gimnázium érettségizett tanulója, Horváth Norbert tanítványa ‐ a BME fizikus hallgatója; Lajkó Kálmán, a Szegedi Radnóti Miklós Kísérleti Gimnázium 12. osztályos tanulója, Mező Tamás tanítványa, valamint Simon Dániel Gábor, a Kecskeméti Bányai Júlia Gimnázium 11. osztályos tanulója, Bakk János tanítványa.
A második díjjal Zimányi Gergely adományából nettó 40 ezer, a harmadik díjjal nettó 25 ezer forint pénzjutalom járt, a díjazottak tanárai pedig a Typotex Kiadó könyvutalványait kapták. A verseny megszervezését az Eötvös Loránd Fizikai Társulat a MOL támogatásából fedezte.