Cím:	Megoldásvázlatok a 2015/4. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Loránt László
Füzet:	2015/május, 267 - 273. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldásvázlatok a 2015/4. sz. emelt szintű gyakorló feladataihoz   I. rész     1. Bizonyítsuk be, hogy $\text{lg}2$ irracionális.  (11 pont)   Megoldás. Bizonyításunk indirekt. Abból indulunk ki, hogy $\text{lg}2$ pozitív valós szám. Ha $\text{lg}2$ racionális szám volna, akkor felírható lenne $p/q$ alakban, ahol $p$ és $q$ pozitív egész számok. A logaritmus fogalma alapján ekkor ${10}^{\frac{p}{q}}=2$, mindkét oldalt $q$-adik hatványra emelve ${10}^p=2^q$. Mivel ${10}^p$ osztható 5-tel, $2^q$ viszont nem, ezért az egyenlőség nem állhat fenn. $\text{lg}2$ tehát nem lehet racionális, ami egy valós szám esetében azt is jelenti, hogy irracionális.   2. $a)$ Hány különböző útvonalon juthatunk el a $8\times 8$-as sakktáblán a bal felső sarokban lévő, az ábrán K-val jelölt mezőről a jobb alsó sarokban lévő, V-vel jelölt mezőre, ha bármely érintett mezőről csak az alatta lévő, vagy a jobb oldalán lévő mezőre léphetünk?     $b)$ Hány olyan útvonal van ezek között, amely a kiinduló mezőtől számított negyedik oszlop és negyedik sor kereszteződésében lévő, T-vel jelölt mezőt nem érinti?  (12 pont)   Megoldás. $a)$ Az 1. ábra illusztrációképpen egy lehetséges útvonalat mutat. 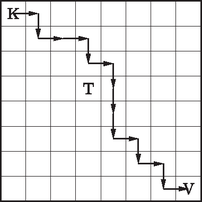  1. ábra   Az útvonalat leírhatjuk egy j (jobbra) és l (lefelé) betűkből álló jelsorozattal is: $\begin{array}{c}{\displaystyle \text{jljjljllljljlj. }}\end{array}$ Bármely útvonal, amely a szabályoknak megfelel, összesen 14 lépésből áll; ezek közül 7 történik jobbra és 7 lefelé. Annyi különböző útvonal van, ahány különböző jelsorozat, mivel a megfelelés kölcsönösen egyértelmű. A különböző útvonalak száma az ismétléses permutációk szerint: $P_{14\left(7;7\right)}^{\text{ism}}=\frac{14!}{7!7!}=3432$. Ugyanerre az eredményre jutunk, ha a $C_{14;7}=\left(\genfrac{}{}{0ex}{}{14}{7}\right)$ kombinációkat vesszük alapul. $b)$ A kérdés megválaszolásához kiszámítjuk, hogy hány különböző útvonal halad át a negyedik oszlop negyedik sorában lévő mezőn (T), és ezt a számot levonjuk az előbb kapott 3432-ből. A kiinduló K mezőből összesen 6 lépéssel jutunk a T mezőre, és ez $\left(\genfrac{}{}{0ex}{}{6}{3}\right)=20$-féleképpen történhet. Innen a V-vel jelölt végállomásra $\left(\genfrac{}{}{0ex}{}{8}{4}\right)=70$-féleképpen juthatunk el. Az első útszakasz bármelyikéhez a második bármelyike párosítható, ezért $20\cdot 70=1400$ útvonal érinti a T mezőt. Ebből következik, hogy $3432-1400=2032$ viszont nem érinti.   3. $a)$ Bizonyítsuk be, hogy ha az $\left(a_n\right)$ végtelen számtani sorozat elemei természetes számok és ezek között van köbszám, akkor a sorozatnak végtelen sok köbszám eleme van. $b)$ Ha például a sorozatban szerepel a $125$, és a sorozat differenciája $3$, akkor lehet-e $125$-nél kisebb köbszám a sorozatban?  ($\text{10}+\text{4}$ pont)   Megoldás. $a)$ Legyen a sorozat köbszám eleme $a_k=c^3$ ($c\ge 0$ egész szám) és $d$ a sorozat differenciája. Ezek ismeretében kiszámíthatjuk $\begin{array}{c}{\displaystyle c^3+\left(3c^2+3cd+d^2\right)d}\end{array}$ értékét. Nyilvánvaló, hogy ez sorozatunk eleme, és ez is köbszám, mégpedig ${\left(c+d\right)}^3$. Könnyen látható ugyanilyen alapon, hogy ${\left(c+2d\right)}^3$, ${\left(c+3d\right)}^3$, $\text{...}$ szintén elemei a sorozatnak. $b)$ 125-nél kisebb nem negatív köbszámok a 0, 1, 8, 27 és 64. Mivel a sorozat differnciája 3, ezek közül csak azok jöhetnek szóba, amelyeknek 125-től való eltérése osztható 3-mal. Ebből a szempontból csak a 8 felel meg. Mármost ha teljesül, hogy a sorozat kezdő eleme $a_1\le 8$, akkor van a sorozatnak 125-nél kisebb köbszám eleme, egyébként nincs.   4. Bútorok hegyes sarkai sérülést okozhatnak. Különösen kisgyermekekre jelentenek veszélyt egy asztal sarkai. Éppen ezért az $\text{1 m<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>×</mo></math>1 m}$-es asztalunk lapját lekerekítettük az asztallap síkjára merőlegesen tartott fűrésszel olyan körívek mentén, amelyek középpontja egybeesik a négyzet alakú felület középpontjával. A négy oldalél mindegyikéből 80 cm hosszú egyenes szakasz maradt meg. Az egyenletes vastagságú asztallap tömege eredetileg 7 kg volt. Mekkora lett a tömege az átalakítás után?  (14 pont)   Megoldás. Osszuk az asztallapot négy egybevágó részre a középvonalak mentén. A négy negyed egyikét a 2. ábra mutatja.   2. ábra   Az ábrázolt felület két derékszögű háromszögből és egy $r$ sugarú körcikkből áll. A háromszögek területe együttvéve $0\mathrm{,}2{\text{m}}^2$. A körcikk középponti szöge $\beta ={90}^{\circ }-2\alpha$, ahol $\text{tg}\alpha =0\mathrm{,}8$. Innen a szögek két tizedesjegy pontossággal: $\begin{array}{c}{\displaystyle \alpha =38\mathrm{,}{66}^{\circ }\text{és}\beta =12\mathrm{,}{68}^{\circ }\mathrm{.}}\end{array}$ A körcikk területe $\begin{array}{c}{\displaystyle \pi r^2\cdot \frac{\beta }{{360}^{\circ }}=\pi \cdot 0\mathrm{,}41{\text{m}}^2\cdot \frac{12\mathrm{,}{68}^{\circ }}{{360}^{\circ }}\approx 0\mathrm{,}045368{\text{m}}^2\mathrm{,}}\end{array}$ mivel $r^2=\left(0\mathrm{,}{5}^2+0\mathrm{,}{4}^2\right){\text{m}}^2=0\mathrm{,}41{\text{m}}^2$. Az asztallap tömege arányos területének nagyságával, amely eredetileg $1{\text{m}}^2$ volt és $4\cdot \left(0\mathrm{,}2+0\mathrm{,}045368\right){\text{m}}^2=0\mathrm{,}98147{\text{m}}^2$ lett, a kérdéses tömeg ezért $7\text{kg}\cdot 0\mathrm{,}98147=6\mathrm{,}870\text{kg}$.   II. rész     5. Egy dobókockával kétszer dobunk. $a)$ Hány elemi esemény alkotja az eseményteret? $b)$ Mekkora annak a valószínűsége, hogy a dobott számok összege legalább $9?$ $c)$ Mekkora annak a feltételes valószínűsége, hogy a dobott számok összege legalább $9$, ha az első dobott szám legalább $5?$ $d)$ Mekkora annak a feltételes valószínűsége, hogy a dobott számok összege legalább $9$, ha az első dobott szám legfeljebb $4?$  ($\text{2}+\text{4}+\text{5}+\text{5}$ pont)   Megoldás. $a)$ Az eseményteret 36 elemi esemény alkotja, amelyet egy $6\times 6$-os táblázattal szemléltetünk (3. ábra). Ez a további kérdések megválaszolásához is hasznos lesz. 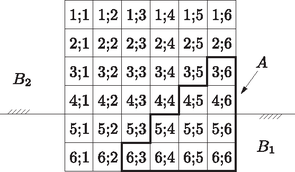  3. ábra   $b)$ A klasszikus valószínűség szerint $P=\frac{k}{n}$ (a kedvező esetek száma osztva a lehetséges esetek számával). Jelölje $A$ azt az eseményt, hogy a dobott számok összege legalább 9. A kedvező esetek száma $k=10$ és $P\left(A\right)=\frac{10}{36}=0\mathrm{,}27\dot{7}$. $c)$ Az $A$ esemény feltételes valószínűsége a $B$ eseményre mint feltételre vonatkozóan: $P\left(A|B\right)=\frac{P\left(AB\right)}{P\left(B\right)}$. $B_1$ jelölje azt az eseményt, hogy az első dobott szám legalább 5. $P\left(B_1\right)=\frac{1}{3}$. Az $A{B}_1$ esemény az $A$ és a $B_1$ halmaz közös része 7 elemi eseményt tartalmaz. $P\left(A{B}_1\right)=\frac{7}{36}$, $\begin{array}{c}{\displaystyle P\left(A|B_1\right)=\frac{\frac{7}{36}}{\frac{1}{3}}=\frac{7}{12}=0\mathrm{,}58\dot{3}\mathrm{.}}\end{array}$ $d)$ Jelölje $B_2$ azt az eseményt, hogy az első dobott szám legfeljebb 4. $P\left(B_2\right)=\frac{2}{3}$. Az $A{B}_2$ eseményt 3 elemi esemény alkotja. $\begin{array}{c}{\displaystyle P\left(A{B}_2\right)=\frac{3}{36}=\frac{1}{12}\text{és}P\left(A|B_2\right)=\frac{\frac{1}{12}}{\frac{2}{3}}=\frac{1}{8}=0\mathrm{,}125.}\end{array}$ A $P\left(A\right)$, $P\left(A|B_1\right)$ és $P\left(A|B_2\right)$ valószínűségeket összehasonlítva megállapítható, hogy a feltételként szereplő esemény a valószínűségeket jelentősen befolyásolhatja kedvező vagy kedvezőtlen irányban is. Megjegyezzük, hogy a feltételes valószínűség meghatározásánál a feltételül szabott esemény tulajdonképpen a biztos esemény szerepét veszi át. Például a $d)$ pontban vizsgált esetben úgy is számolhatunk, hogy $B_2$ 24 elemi eseményből álló eseménytér, amelyen belül a kedvező esetek száma 3, a valószínűség pedig $\frac{3}{24}=\frac{1}{8}$.   6. Az $f\left(x\right)=x^3+a{x}^2+2x$ függvényről tudjuk, hogy inflexiós érintője párhuzamos az $x+y=0$ egyenletű egyenessel. Határozzuk meg az $a$ együttható értékét. Igazoljuk, hogy a függvény inflexiós pontja az $x$-tengelyen van.  (16 pont)   Megoldás. Az $f\left(x\right)$ függvény első deriváltja: $f\text{'}\left(x\right)=3x^2+2ax+2$. Ez bármely helyen megadja az érintő meredekségét. A második derivált: $f\text{'}\text{'}\left(x\right)=6x+2a$. $f\text{'}\text{'}\left(x\right)=0$, ha $x_0=-\frac{a}{3}$. Itt a függvénynek inflexiós pontja van, mivel $f\text{'}\text{'}\left(x\right)$ $x_0$-nál előjelet vált (negatívból pozitívba). Az inflexiós érintő meredeksége az $x+y=0$ egyenletű egyenessel való párhuzamosság folytán $-1$. Tehát $\begin{array}{c}{\displaystyle f\text{'}\left(x_0\right)=3\cdot \frac{a^2}{9}-2\cdot \frac{a^2}{3}+2=-\mathrm{1,}}\end{array}$ innen $a^2=9$, vagyis $a_1=3$, $a_2=-3$. Ha $a_1=3$, akkor $x_{01}=-1$ és $f\left(x_{01}\right)=0$. Ha pedig $a_2=-3$, akkor $x_{02}=1$ és $f\left(x_{02}\right)$ szintén egyenlő 0-val, tehát az inflexiós pont mindkét esetben az $x$-tengelyen van.   7. Bizonyítsuk be, hogy $\begin{array}{c}{\displaystyle \sqrt[]{\text{sin}x}+\sqrt[]{\text{cos}x}\le \sqrt[4]{8}\mathrm{,}}\end{array}$ ha $0\le x\le \frac{\pi }{2}$.  (16 pont)   Megoldás. Mivel a bizonyítandó egyenlőtlenség mindkét oldalán pozitív mennyiségek állnak, ezek négyzetei között fennálló reláció az eredeti egyenlőtlenségre is igaz. Tehát elég azt bizonyítani, hogy ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{sin}x+\text{cos}x+2\sqrt[]{\text{sin}x\cdot \text{cos}x}\le \sqrt[]{8}\left(0\le x\le \frac{\pi }{2}\right)\mathrm{.}}\hfill \\ \hfill {\displaystyle \text{sin}x+\text{cos}x=\sqrt[]{{\left(\text{sin}x+\text{cos}x\right)}^2}=\sqrt[]{\text{sin}{}^{2}x+\text{cos}{}^{2}x+2\text{sin}x\text{cos}x}=\sqrt[]{1+\text{sin}2x}\le \sqrt[]{2}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle }\hfill \\ \hfill {\displaystyle \text{és}}\hfill \\ \hfill {\displaystyle 2\sqrt[]{\text{sin}x\text{cos}x}=\sqrt[]{2}\sqrt[]{\text{sin}2x}\le \sqrt[]{2}\mathrm{,}}\hfill & \text{(<mn>2</mn>)}\end{array}}$ ezért a bal oldal $2\sqrt[]{2}$-nél, vagyis $\sqrt[]{8}$-nál nem lehet nagyobb.   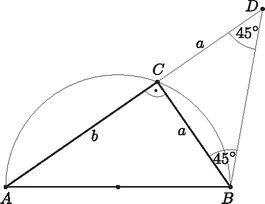8. Szerkesszünk derékszögű háromszöget, ha adott a beírt és a körülírt körének sugara. Mi a megoldhatóság feltétele? (Elegendő a szerkesztés menetét leírni.)  (16 pont)   Megoldás. Jelölje $\varrho$ a beírt, $r$ pedig a körülírt kör sugarát. (A derékszögű háromszög oldalait a szokásos módon jelöljük.) A Thalész-tétel értelmében $c=2r$. A beírt kör sugarára fennáll: $c=a+b-2\varrho$. Ehhez azt kell látni (4. ábra), hogy a derékszög csúcsánál kialakul egy $\varrho$ oldalú négyzet, továbbá azt, hogy külső pontból egy körhöz húzott érintőszakaszok egyenlők.   4. ábra   A felírt összefüggésekből $2\left(r+\varrho \right)=a+b$. A feladat ezek után úgy is szólhatna, hogy szerkesszünk derékszögű háromszöget, ha adott az átfogója és a két befogó összege. Ehhez a 5. ábra ad segítséget. Az $ABC$ derékszögű háromszög $b$ befogójának meghosszabbítására felmértük az $a$ befogót: $AD=a+b$.   5. ábra   Mivel $BCD$ egyenlő szárú derékszögű háromszög, a $D$-nél fekvő szöge ${45}^{\circ }$. Ezek alapján a szerkesztés menete a következő. Egy ${45}^{\circ }$-os szög egyik szárára a $D$ csúcsból kiindulva felmérjük az $a+b$ hosszúságú szakaszt: így kapjuk az $A$ pontot. A másik szárból kimetsszük azt a $B$ pontot, amely az $A$ ponttól $c=2r$ távolságra van. Mivel az $ABD$ háromszög megszerkesztéséhez két oldal és a kisebbikkel szemközti szög áll rendelkezésre (nem egybevágósági alapeset), általában két megfelelő csúcspont, $B_1$ és $B_2$ adódik (6. ábra).   6. ábra   A megszerkeszteni kívánt $ABC$ derékszögű háromszög $C$ csúcsát a $B_1$, illetve a $B_2$ pontból az $AD$ szakaszra bocsátott merőlegesek $C_1$, illetve $C_2$ talppontja adja. Habár két háromszöget kaptunk, a megoldás egyértelmű, mivel az $A{B}_1{C}_1$ és $A{B}_2{C}_2$ háromszögek egybevágóak. Ezt az átfogók és az $\alpha$-val jelölt hegyesszögek egyenlősége biztosítja. (Az $\alpha$ szög az $A{B}_2{C}_2$ háromszögben a $B_2$ csúcsnál fekszik.) Abban az esetben, ha $c\sqrt[]{2}=a+b$, akkor $B_1$ és $B_2$ egybeesik: az $ABC$ háromszög egyenlő szárú. Ha $c\sqrt[]{2}<a+b$, akkor nincs megoldás. Más szóval a megoldhatóság feltétele: $2r\sqrt[]{2}\ge 2\left(r+\varrho \right)$, vagyis $\varrho \le r\left(\sqrt[]{2}-1\right)$.   9. Egy harckocsizó alakulatnál szolgáló férfiak $40$ fős csoportjában a testmagasság $\left(x_i\right)$ és a testtömeg $\left(y_i\right)$ adatait a következő táblázat tartalmazza:   ${\displaystyle \begin{array}{|cc|}\hline \hfill {\displaystyle \text{testmagasság <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>x</mi></mrow><mrow><mi>i</mi></mrow></msub></mrow></math> [cm] }}\hfill & \hfill {\displaystyle \text{ testtömeg <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>y</mi></mrow><mrow><mi>i</mi></mrow></msub></mrow></math> [kg]}}\hfill \\ \hfill {\displaystyle \text{162 }}\hfill & \hfill {\displaystyle \text{ 70, 77}}\hfill \\ \hfill {\displaystyle \text{163 }}\hfill & \hfill {\displaystyle \text{ 61 }}\hfill \\ \hfill {\displaystyle \text{164 }}\hfill & \hfill {\displaystyle \text{ 58, 64, 68}}\hfill \\ \hfill {\displaystyle \text{165 }}\hfill & \hfill {\displaystyle \text{ 73 }}\hfill \\ \hfill {\displaystyle \text{166 }}\hfill & \hfill {\displaystyle \text{ 62, 65, 70}}\hfill \\ \hfill {\displaystyle \text{167 }}\hfill & \hfill {\displaystyle \text{ 65, 66, 75, 80}}\hfill \\ \hfill {\displaystyle \text{168 }}\hfill & \hfill {\displaystyle \text{ 63, 69, 71, 79}}\hfill \\ \hfill {\displaystyle \text{169 }}\hfill & \hfill {\displaystyle \text{ 64, 70, 75, 76}}\hfill \\ \hfill {\displaystyle \text{170 }}\hfill & \hfill {\displaystyle \text{ 58, 61, 71, 75, 75, 88}}\hfill \\ \hfill {\displaystyle \text{171 }}\hfill & \hfill {\displaystyle \text{ 67, 68, 75, 77}}\hfill \\ \hfill {\displaystyle \text{172 }}\hfill & \hfill {\displaystyle \text{ 61, 65, 70, 84}}\hfill \\ \hfill {\displaystyle \text{173 }}\hfill & \hfill {\displaystyle \text{ 58, 77}}\hfill \\ \hfill {\displaystyle \text{174 }}\hfill & \hfill {\displaystyle \text{ 63, 80}}\hfill \\ \hline\end{array}}$   $a)$ Ha a kg-ban mért testtömeget a m-ben mért testmagasság négyzetével elosztjuk, akkor az úgynevezett testtömeg-indexet kapjuk. A katonaorvos egy bizonyos egész számnál nagyobb testtömeg-index esetén minősít valakit túlsúlyosnak. 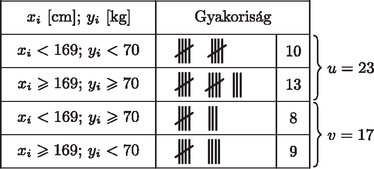Mekkora ez az érték, ha az orvos szerint a szóbanforgó csoportban a túlsúlyosok aránya $10\%?$ $b)$ Számítsuk ki az $\overline{x}$ és $\overline{y}$ átlagokat. Jelölje $u$ azoknak az $\left(x_i\mathrm{,}{y}_i\right)$ értékpároknak a számát, amelyeknél a két adat az átlaghoz képest ugyanabban az irányban tér el, $v$ pedig azoknak a számát, ahol az eltérés ellentétes irányú. Számítsuk ki az $\frac{u-v}{u+v}$ hányadost. Mire következtethetünk ebből?  ($\text{8}+\text{8}$ pont)   Megoldás. $a)$ Azt a négy egyént kell megtalálnunk, akiknek a testtömeg-indexe a 40 fős alakulatban a legnagyobb. Ezek:   ${\displaystyle \begin{array}{|ccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>x</mi></mrow><mrow><mi>i</mi></mrow></msub></mrow></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>y</mi></mrow><mrow><mi>i</mi></mrow></msub></mrow></math> }}\hfill & \hfill {\displaystyle \text{ Index}}\hfill \\ \hfill {\displaystyle \text{170 }}\hfill & \hfill {\displaystyle \text{ 88 }}\hfill & \hfill {\displaystyle \text{ 30,45}}\hfill \\ \hfill {\displaystyle \text{162 }}\hfill & \hfill {\displaystyle \text{ 77 }}\hfill & \hfill {\displaystyle \text{ 29,34 }}\hfill \\ \hfill {\displaystyle \text{167 }}\hfill & \hfill {\displaystyle \text{ 80 }}\hfill & \hfill {\displaystyle \text{ 28,69 }}\hfill \\ \hfill {\displaystyle \text{172 }}\hfill & \hfill {\displaystyle \text{ 84 }}\hfill & \hfill {\displaystyle \text{ 28,39 }}\hfill \\ \hline\end{array}}$   A következő $\left(168;79\right)$ már csak 27,99. Természetesen ehhez nem szükséges mind a negyven adatot kiszámítani, de azért körültekintően kell eljárni. Az orvos tehát 28-nál nagyobb testtömeg-index esetén minősít valakit túlsúlyosnak. $b)$ Az átlagok: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \overline{x}}& {\displaystyle =\frac{6744}{40}=\mathrm{168,6}\text{cm}\mathrm{,}}\hfill \\ \hfill {\displaystyle \overline{y}}& {\displaystyle =\frac{2794}{40}=\mathrm{69,85}\text{kg}\mathrm{.}}\hfill \end{array}}$ Az adatpárokat négy kategóriába sorolva:     A keresett hányados: $\frac{u-v}{u+v}=\frac{6}{40}=0\mathrm{,}15$. Ez azt jelzi, hogy a testmagasság és a testtömeg között milyen szoros a kapcsolat. Értéke nyilván $+1$ és $-1$ között mozoghat. Ha $x_i$ és $y_i$ minden esetben ugyanabba az irányba térne el az átlagtól, akkor $+1$, ha pedig minden esetben ellentétes irányú lenne az eltérés, akkor $-1$ volna az értéke. Ezek nagyon erős összefüggést jelentenének. Ha viszont a hányados 0, akkor a két jellemző egymástól függetlennek tekinthető. Esetünkben a 0,15-os érték azt mutatja, hogy a testmagasság és testtömeg között meglepően gyenge a kapcsolat, bár igaz, hogy az átlagosnál magasabb egyének körében az átlagosnál nagyobb tömegűek felé billen a mérleg.