Cím:	Szakaszok ekvioptikus görbéi
Szerző(k):	Fehér Zsombor
Füzet:	2015/május, 258 - 267. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Szakaszok ekvioptikus görbéi     Bevezető Ekvioptikus, azaz egyenlő látószögű. Ha adott a síkon két görbe, úgy azok ekvioptikus görbéjén (röviden ekvioptikusán) azon pontok mértani helyét értjük, melyekből a két görbe ugyanakkora szögben látszik. A látószög annak a legkisebb szögnek a nagysága, amelynek szögszárain kívül nincs pontja a görbének. Találkozhatunk még az izoptikus kifejezéssel, mely jelentése állandó látószögű. Adott egy síkgörbe és egy rögzített $\alpha$ szög. Ekkor azon pontok mértani helye, melyekből a görbe $\alpha$ szögben látszik, a görbe $\alpha$-izoptikusa. Amennyiben $\alpha ={90}^{\circ }$, úgy az $\alpha$-izoptikust ortoptikusnak is nevezzük. Két görbe azonos szögű izoptikusainak metszéspontjai alkotják tehát az ekvioptikus görbét. Az olvasó például meggondolhatja, hogy két nem metsző kör ekvioptikusa egy harmadik kör, egy parabola ortoptikusa egyenes, míg az ellipszisek és hiperbolák ortoptikusai körök. Az ellipszisek és hiperbolák $\alpha$-izoptikusai általában negyedrendű görbék. Jelen cikkünkben szakaszok ekvioptikusait fogjuk vizsgálni, azzal a kiegészítéssel, hogy a szögeket irányítottan nézzük, modulo ${180}^{\circ }$. Ez biztosítja azt a kényelmet, hogy például egy szakasz $\alpha$-izoptikusa a teljes körvonal legyen (ne pedig két külön körív, melyek egymás tükörképei a szakasz egyenesére).   Definíció. Adottak a síkon az $A$, $B$, $C$, $D$ pontok. Az $AB$ és $CD$ szakaszok ekvioptikus görbéjének nevezzük és $S\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)$-vel jelöljük azon pontok mértani helyét, melyekből a két szakasz egyenlő irányított szögben látszik: $\begin{array}{c}{\displaystyle S\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)=\left\{P\mid APB\sphericalangle \equiv CPD\sphericalangle \left(\text{mod}{180}^{\circ }\right)\right\}\mathrm{.}}\end{array}$ Megjegyezzük, hogy pl. $A$-hoz ``nagyon közeli'' $P$ pontokra az $APB\sphericalangle$ minden lehetséges értéket felvesz, ezért $P=A$ esetén a fenti egyenlőséget igaznak tekintjük. Tehát az $A$, $B$, $C$, $D$ pontok is elemei a fenti halmaznak.   A görbe néhány tulajdonsága 1. állítás. Két szakasz ekvioptikusa mindig egy legfeljebb harmadrendű görbe.   Bizonyítás. Legyenek a pontok koordinátái $A\left(a_1\mathrm{,}{a}_2\right)$, $B\left(b_1\mathrm{,}{b}_2\right)$, $C\left(c_1\mathrm{,}{c}_2\right)$, $D\left(d_1\mathrm{,}{d}_2\right)$ és $P\left(x\mathrm{,}y\right)$, továbbá legyen $P$ merőleges vetülete az $y$-tengelyre $X\left(\mathrm{0,}y\right)$ (1. ábra). Ekkor az $APB$ szög tangense kifejezhető az $AP$ és $BP$ szakaszok $m_a$, $m_b$ meredeksége, és a tangens addíciós képlete alapján: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{tg}APB\sphericalangle }& {\displaystyle =\frac{\text{tg}APX\sphericalangle -\text{tg}BPX\sphericalangle }{1+\text{tg}APX\sphericalangle \text{tg}BPX\sphericalangle }=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{m_a-m_b}{1+m_a{m}_b}=\frac{\frac{y-a_2}{x-a_1}-\frac{y-b_2}{x-b_1}}{1+\frac{y-a_2}{x-a_1}\cdot \frac{y-b_2}{x-b_1}}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{\left(y-a_2\right)\left(x-b_1\right)-\left(y-b_2\right)\left(x-a_1\right)}{\left(x-a_1\right)\left(x-b_1\right)+\left(y-a_2\right)\left(y-b_2\right)}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{f_1\left(x\mathrm{,}y\right)}{f_2\left(x\mathrm{,}y\right)}\mathrm{.}}\hfill \end{array}}$ A számlálóban az $xy$ tag éppen kiesik, ezért $f_1$ elsőfokú, $f_2$ pedig másodfokú polinom. Ugyanígy, $\text{tg}CPD\sphericalangle =g_1\left(x\mathrm{,}y\right)/g_2\left(x\mathrm{,}y\right)$, ahol $g_1$ elsőfokú, $g_2$ másodfokú. Mivel $\text{tg}APB\sphericalangle =\text{tg}CPD\sphericalangle$ éppen ekvivalens azzal, hogy $APB\sphericalangle \equiv CPD\sphericalangle \left(\text{mod}{180}^{\circ }\right)$, a keresett görbe egyenlete $f_1/f_2=g_1/g_2$, azaz $0=f_1{g}_2-f_2{g}_1$, ami valóban (legfeljebb) harmadrendű görbe.   1. ábra     2. állítás. Amennyiben $ABDC$ deltoid, úgy $S\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)$ egy kör és egy egyenes uniója.   1. bizonyítás (Koordinátageometria). Legyen a deltoid szimmetriatengelye pl. $BC$, és vegyük fel a koordináta-rendszert úgy, hogy $BC$ legyen az $x$-tengely, $AD$ pedig az $y$-tengely. Ekkor $a_1=0$, $b_2=0$, $c_2=0$, $d_1=0$, $a_2+d_2=0$, így a $0=f_1{g}_2-f_2{g}_1$ egyenlet egy kis számolással a következő alakra hozható: $\begin{array}{c}{\displaystyle 0=y\cdot \left(\left(x^2+y^2\right)\left(b_1+c_1\right)+x\left(2a_2^2-2b_1{c}_1\right)-a_2^2\left(b_1+c_1\right)\right)\mathrm{.}}\end{array}$ Az első tényező az $y=0$ egyenes, a második tényező pedig egy kör egyenlete, hiszen $x^2$ és $y^2$ együtthatói megegyeznek, és nincs $xy$ tag. Ebből a megoldásból az derült ki, hogy az egyenes a deltoid szimmetriatengelye, a kör pedig tükrös erre az egyenesre.   2. bizonyítás (Apollóniusz-kör). Vegyünk egy tetszőleges $P$ pontot az ekvioptikus görbéről, és legyen $T$ az $APD$ kör és a $BC$ egyenes (egyik) metszéspontja (2. ábra, az ekvioptikus szaggatott vonallal van jelölve). Ekkor szimmetria miatt $T$ az $AD$ ív felezőpontja, így $APT\sphericalangle \equiv TPD\sphericalangle$. Ezt hozzáadva ahhoz, hogy $BPA\sphericalangle \equiv DPC\sphericalangle$, azt kapjuk, hogy 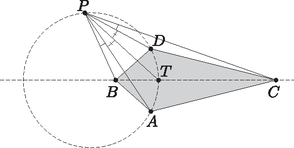$BPT\sphericalangle \equiv TPC\sphericalangle \left(\text{mod}{180}^{\circ }\right)$.   2. ábra   Az $APDT$ kör tükrös $BC$-re, és $T$ rajta van $BPC\sphericalangle$ szögfelezőjén, ezért ez a kör nem más, mint a $B$, $C$ pontok $T$-n átmenő Apollóniusz-köre (amennyiben $P$ nincs rajta a $BC$ egyenesen). Mivel $D$ is rajta van ezen az Apollóniusz körön, ezért tetszőleges $P$ pont esetén $BP/PC=BD/DC$, vagyis az $APDT$ kör állandó. Így $P$ mértani helye a $B$, $C$ pontok $D$-n átmenő Apollóniusz-köre, továbbá a nyilvánvaló $BC$ egyenes. Ebből a megoldásból az is kiderült, hogy a mértani helyként kapott kör nem csak egyszerűen tükrös az egyenesre, hanem egy konkrét Apollóniusz kör. Ezt szintén érdemes megjegyezni.   3. bizonyítás (Forgatva nyújtás). Legyen $M$ azon $\phi$ forgatva nyújtás középpontja, melyre $\phi \left(AB\right)=CD$ (3. ábra). Ismert, hogy ekkor $M$ rajta van az $AB$, $BD$, $DC$, $CA$ egyenesek közül bármely három által meghatározott háromszög köréírt körén. Legyen $P$ egy pont az $M$ középpontú $MD$ sugarú $k$ körön. Amennyiben a $\phi$ forgatva nyújtás során az $ABP$ háromszög képe $CDP\text{'}$, úgy létezik olyan $M$ középpontú $\phi \text{'}$ forgatva nyújtás is, melyre $\phi \text{'}\left(BD\right)=PP\text{'}$.   3. ábra   Ekkor a $\phi$ forgatva nyújtás miatt $MD{C}_{▵}\sim MB{A}_{▵}$, a deltoid szimmetriája miatt az $MB{A}_{▵}$ és $MB{D}_{▵}$ háromszögek egybevágóak és ellentétes körüljárásúak, a $\phi \text{'}$ forgatva nyújtás miatt pedig $MB{D}_{▵}\sim MPP{\text{'}}_{▵}$. Mivel olyan $P$ pontot vettünk, ami rajta van $k$-n, tehát $MD=MP$, ezért az $MD{C}_{▵}$ és $MPP{\text{'}}_{▵}$ háromszögek egybevágóak és ellentétes körüljárásúak. Ez pedig azt jelenti, hogy $CDPP\text{'}$ húrtrapéz, így $DPC\sphericalangle \equiv DP\text{'}C\sphericalangle \equiv BPA\sphericalangle \left(\text{mod}{180}^{\circ }\right)$, a $\phi$ forgatva nyújtást is használva. Így a $k$ kör minden $P$ pontja rajta van $S\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)$-n, továbbá a $BC$ egyenes is rajta van, és tudva, hogy a görbe harmadrendű, ezért más pontja nincs is.   A 2. állításra fogunk adni egy 4. bizonyítást is, ehhez azonban meg kell ismernünk a Cserebere-tételt (csak a cikkben nevezzük így).   A Cserebere-tétel Elérkeztünk cikkünk fő attrakciójához. A most következő tétel arról szól, hogy ekvioptikus görbét valójában nem két szakaszhoz rendelünk, hanem négy egyeneshez.   3. állítás (Cserebere-tétel). Adottak a síkon az $a$, $b$, $c$, $d$ egyenesek, melyek közül semelyik háromnak sincs közös pontja. Kiválasztunk közülük kettőt, pl. $a$-t és $b$-t, majd tekintjük azt a két szakaszt, amit a másik két egyenes, $c$ és $d$ metsz ki belőlük. Ekkor ezen két szakasz ekvioptikus görbéje nem függ attól, hogy melyik két egyenest választottuk ki. Tehát például $b$ és $c$ felcserélhető: $\begin{array}{c}{\displaystyle S\left(a\cap c\mathrm{,}a\cap d\mathrm{,}b\cap c\mathrm{,}b\cap d\right)=S\left(a\cap b\mathrm{,}a\cap d\mathrm{,}c\cap b\mathrm{,}c\cap d\right)\mathrm{.}}\end{array}$ A 4. ábra jobb oldali részén a lehetséges $\overrightarrow{AB}$ és $\overrightarrow{CD}$ vektorok vannak berajzolva. A Cserebere-tétel szerint a hat ábra közül bármelyik esetén $S\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)$ a bal oldali harmadrendű görbe lesz. 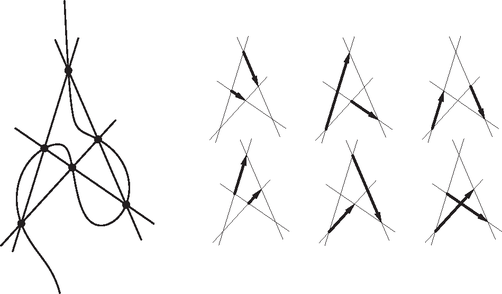  4. ábra   A bizonyításhoz kettősviszonyokat fogunk használni. A projektív geometriáról és kettősviszonyról bővebben az [1], [2], vagy [3] hivatkozásokban lehet olvasni. 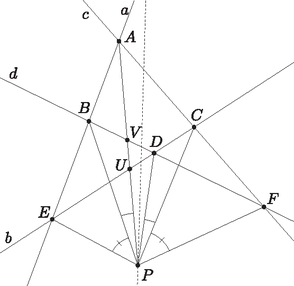  Bizonyítás. Legyen $A=a\cap c$, $B=a\cap d$, $C=b\cap c$, $D=b\cap d$, $E=a\cap b$, $F=c\cap d$, $U=AP\cap b$ és $V=AP\cap d$ (5. ábra). Megmutatjuk, hogy ha $APB\sphericalangle \equiv CPD\sphericalangle$, akkor $BPE\sphericalangle \equiv FPC\sphericalangle \left(\text{mod}{180}^{\circ }\right)$, minden más egyenesfelcserélés ezzel egyenértékű állításhoz vezet. Az $A$ pontból $d$-ről $b$-re való vetítés során a következő kettősviszony megmarad: $\begin{array}{c}{\displaystyle \left(BVDF\right)=\left(EUDC\right)\mathrm{.}}\end{array}$ Tetszőleges kettősviszony ,,visszafelé'' is leírható, így $\left(EUDC\right)=\left(CDUE\right)$. A $P$ körüli sugársorokkal megfogalmazva ugyanezt: $\begin{array}{c}{\displaystyle \left(PB\mathrm{,}PA\mathrm{,}PD\mathrm{,}PF\right)=\left(PC\mathrm{,}PD\mathrm{,}PA\mathrm{,}PE\right)\mathrm{.}}\end{array}$ Az $APD\sphericalangle$ szögfelezőjére tükrözve $PA$ képe $PD$, és $PB$ képe $PC$. Egy kettősviszony értéke és három egyenese alapján a negyedik egyenes egyértelmű, ezért az előző kettősviszonyok csak akkor lehetnek egyenlők, ha $PE$ képe $PF$. Ekkor $BPE\sphericalangle \equiv FPC\sphericalangle \left(\text{mod}{180}^{\circ }\right)$, így a Cserebere-tételt beláttuk.   5. ábra   2. állítás, 4. bizonyítás (Cserebere-tétel). Legyenek az $ABDC$ deltoid szemközti oldalainak metszéspontjai $E=AB\cap CD$ és $F=AC\cap BD$ (6. ábra). Ekkor a Cserebere-tétel szerint $S\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)=S\left(A\mathrm{,}F\mathrm{,}E\mathrm{,}D\right)$. Azonban az $AFED$ húrtrapéz szárainak ekvioptikusát könnyű megtalálni: szimmetria miatt a $BC$ egyenes, a kerületi szögek tétele miatt pedig az $AFED$ kör minden pontja rajta van az ekvioptikus görbén. Tehát deltoid esetén az ekvioptikus valóban egy kör és egy egyenes uniója. 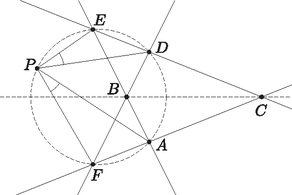  6. ábra     A köri ideális pontok Komplex projektív síknak nevezzük azon $\left(x\mathrm{,}y\mathrm{,}z\right)\ne \left(\mathrm{0,0,0}\right)$, $x\mathrm{,}y\mathrm{,}z\in \text{C}$ komplex számhármasok halmazát, melyben az $\left(x\mathrm{,}y\mathrm{,}z\right)$ és $\left(\lambda x\mathrm{,}\lambda y\mathrm{,}\lambda z\right)$ pontokat azonosnak tekintjük minden $\lambda \ne 0$, $\lambda \in \text{C}$ esetén. A valós projektív síkot úgy lehet elképzelni, hogy a 3-dimenziós euklideszi térben az origón átmenő $\left\{\left(\lambda x\mathrm{,}\lambda y\mathrm{,}\lambda z\right)\mid \lambda \in \text{R}\right\}$ egyeneseket elmetsszük a $z=1$ síkkal. Amelyik egyenest tényleg elmetszi, ott kapunk valódi $\left(x\mathrm{,}y\right)$ pontot, amelyik egyenes pedig párhuzamos vele, abban az esetben beszélünk ideális pontról. A komplex projektív síkon sincs ez másképp: az $\left(x\mathrm{,}y\mathrm{,0}\right)$ pontokat nevezzük ideális pontoknak. Mivel $\left(x\mathrm{,}y\mathrm{,}z\right)=\left(\lambda x\mathrm{,}\lambda y\mathrm{,}\lambda z\right)$, a projektív síkon minden alakzat egyenlete homogén $x$, $y$, $z$-re nézve. Így egy kör egyenlete az $x^2+y^2+axz+byz+c{z}^2=0$ alakot ölti. Habár az euklideszi síkon nevetségesnek tűnik a kérdés, mégis megkérdezhetjük: van-e a körnek ideális pontja? A meglepő válasz erre az, hogy a komplex síkon igenis van. Ugyanis $z=0$ helyettesítéssel $x^2+y^2=0$ adódik, melynek van nemnulla megoldása: az $y=\pm ix$. Ami még meglepőbb, hogy az így kapott $\begin{array}{c}{\displaystyle \left(\mathrm{1,}i\mathrm{,0}\right)\mathrm{,}\left(\mathrm{1,}-i\mathrm{,0}\right)}\end{array}$ pontok minden lehetséges körön rajta vannak. Van tehát két olyan pont valahol a komplex végtelenben, melyek minden körre illeszkednek. Ezért ezeket a pontokat köri ideális pontoknak nevezzük.   Ha adott két kör egyenlete: $k_1$ és $k_2$, akkor tetszőleges $\lambda \mathrm{,}\mu$ esetén $\lambda k_1+\mu k_2$ is egy kör egyenlete. A $\text{K}=\left\{\lambda k_1+\mu k_2\mid \lambda \mathrm{,}\mu \in \text{R}\right\}$ halmazt körsornak nevezzük. Körsorok segítségével adhatunk egy újabb módot az ekvioptikus görbe előállítására: adott egy $\text{K}$ körsor és egy $\phi$ forgatva nyújtás, és a körsor minden $k$ köréhez vesszük a forgatva nyújtás szerinti képével való metszéspontjait, tehát a $\begin{array}{c}{\displaystyle \left\{k\cap \phi \left(k\right)\mid k\in \text{K}\right\}}\end{array}$ halmazt. Ha $\text{K}$ hiperbolikus, azaz fix $A$, $B$ pontokon átmenő körsor, és $\phi \left(AB\right)=CD$, akkor $\left\{k\cap \phi \left(k\right)\mid k\in \text{K}\right\}=S\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)$, hiszen az $AB$ szakasz $\alpha$ szögű látókörének képe a $CD$ szakasz $\alpha$ szögű látóköre lesz, így metszéspontjuk rajta van az ekvioptikus görbén. A köri ideális pontok bármely két kör metszetén rajta vannak, ezért benne vannak a $\left\{k\cap \phi \left(k\right)\mid k\in \text{K}\right\}$ halmazban is, és mivel ez a körsoros előállítás ugyanazt a ponthalmazt adja, mint az ekvioptikus görbés előállítás, a köri ideális pontok tetszőleges ekvioptikus görbén rajta vannak. Ugyanerről persze meggyőződhetünk az 1. állításbeli $0=f_1{g}_2-f_2{g}_1$ egyenletbe való helyettesítéssel is. Annak, hogy az ekvioptikus egy olyan speciális harmadrendű görbe, ami átmegy a köri ideális pontokon, egy következménye a   4. állítás. Amennyiben két szakasz ekvioptikusa tartalmaz egy valódi (azaz nem komplex és nem ideális) egyenest, akkor a görbe maradék része egy kör.   Bizonyítás. Tegyük fel, hogy a harmadrendű görbe $\begin{array}{c}{\displaystyle \left(Ax+By+C\right)\left(D{x}^2+Exy+F{y}^2+Gx+Hy+I\right)=0}\end{array}$ alakban felbomlik egy elsőfokú és egy másodfokú polinom szorzatára, ahol az együtthatók mind valós számok. Tudjuk, hogy ezen a görbén rajta vannak a köri ideális pontok, így homogenizálva, majd $\begin{array}{c}{\displaystyle \left(x\mathrm{,}y\mathrm{,}z\right)=\left(\mathrm{1,}i\mathrm{,0}\right)}\end{array}$ helyettesítéssel: $\begin{array}{c}{\displaystyle \left(A+Bi\right)\left(D+Ei-F\right)=0.}\end{array}$ Az első tényező csak akkor lehet nulla, ha $A=B=0$, azonban ez nem ad valódi egyenest. Így a második tényezőnek kell nullának lennie, ahonnan $D=F$ és $E=0$, azaz a másodfokú tényezőben $x^2$ és $y^2$ együtthatói megegyeznek, továbbá nincs $xy$ tag. Ez pedig éppen azt jelenti, hogy a harmadrendű görbe egy egyenes és egy (valós vagy képzetes) kör uniója.   Tulajdonképpen azt használtuk, hogy ha egy másodrendű görbe átmegy a köri ideális pontokon, akkor az a görbe egy kör. Megjegyzendő azonban a paralelogramma esete: ha $\overrightarrow{AB}=\overrightarrow{CD}$, akkor $S\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)$ felbomlik ugyan egy egyenes és egy másodrendű görbe uniójára, de mégsem tartalmaz kört. Ebben az esetben ugyanis az egyenes az ideális egyenes, tehát a köri ideális pontokon az $Ax+By+C=0$ egyenletű alakzat megy át. A köri ideális pontok segítségével újabb bizonyítást adhatunk a 2. állításra és a Cserebere-tételre:   2. állítás, 5. bizonyítás (Köri ideális pontok). A deltoid szimmetriatengelye nyilvánvalóan része az ekvioptikus görbének. A 4. állítás alapján pedig a maradék egy kör, így készen vagyunk. (Az is könnyen megállapítható, hogy melyik kör, ugyanis a 6. ábra jelöléseivel az $A$, $D$, $E$, $F$ pontoknak rajta kell lenniük az ekvioptikuson, tehát a körön is.) Cserebere-tétel, 2. bizonyítás. Legyen a négy egyenes 6 metszéspontja a szokásos módon $A$, $B$, $C$, $D$, $E$, és $F$ (7. ábra). Ekkor ez a 6 pont rajta van bármelyik ekvioptikuson, pl. $S\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)$-n és $S\left(E\mathrm{,}B\mathrm{,}C\mathrm{,}F\right)$-en. A két köri ideális pont: $I_1$ és $I_2$ is mindkettőn rajta van. Miquel tétele szerint tetszőleges négy egyenesre az $ABF$, $ACE$, $CDF$, $BDE$ köröknek van közös pontja. Ha ez a közös pont $M$, akkor $AMB\sphericalangle \equiv AFB\sphericalangle \equiv CFD\sphericalangle \equiv CMD\sphericalangle \left(\text{mod}{180}^{\circ }\right)$, így $M$ rajta van $S\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)$-n, és ugyanígy rajta van $S\lef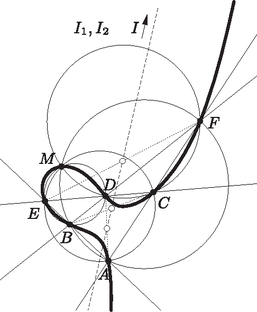t(E\mathrm{,}B\mathrm{,}C\mathrm{,}F\right)$-en is.   7. ábra   Keressük meg $S\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)$ valós ideális pontját: ehhez az 1. állításbeli $0=f_1{g}_2-g_1{f}_2$ egyenlet homogenizált alakját írjuk fel, majd $z=0$-t helyettesítünk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 0}& {\displaystyle =\left(b_{2}x+a_{1}y-a_{2}x-b_{1}y\right)\left(x^2+y^2\right)-\left(d_{2}x+c_{1}y-c_{2}x-d_{1}y\right)\left(x^2+y^2\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle =x\left(b_2+c_2-a_2-d_2\right)-y\left(b_1+c_1-a_1-d_1\right)\mathrm{.}}\hfill \end{array}}$ Tehát $S\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)$ ideális pontja az $I\left(b_1+c_1-a_1-d_1\mathrm{,}{b}_2+c_2-a_2-d_2\mathrm{,0}\right)$ pont. Az $AD$ és $BC$ szakaszok felezőpontjai $U\left(\frac{a_1+d_1}{2}\mathrm{,}\frac{a_2+d_2}{2}\mathrm{,1}\right)$ és $V\left(\frac{b_1+c_1}{2}\mathrm{,}\frac{b_2+c_2}{2}\mathrm{,1}\right)$, így a koordináták $I=2\left(V-U\right)$ összefüggése alapján $I$, $U$, $V$ egy egyenesre esik. Ismert, hogy tetszőleges négy egyenesre az $AD$, $BC$, $EF$ szakaszok felezőpontjai egy egyenesre esnek, így $I$ rajta van $S\left(E\mathrm{,}B\mathrm{,}C\mathrm{,}F\right)$-en is. Tehát van 10 különböző pontunk (különbözőek, mert az állítás 4 általános helyzetű egyenesről szólt): $A$, $B$, $C$, $D$, $E$, $F$, $M$, $I_1$, $I_2$, és $I$, melyek rajta vannak $S\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)$-n és $S\left(E\mathrm{,}B\mathrm{,}C\mathrm{,}F\right)$-en is. Márpedig két teljesen különböző harmadrendű görbének legfeljebb csak 9 metszéspontja lehet, ha 10 van, az azt jelenti, hogy van közös komponensük. Tegyük fel, hogy a két görbe nem azonos, ekkor mindkettő felbomlik egy egyenesre és egy másodfokú görbére. Ha az egyenes részük különböző, akkor azoknak legfeljebb 1 metszéspontjuk lehet a 10-ből, azonban a maradék 9 pontra nem illeszthető másodrendű görbe, akármelyik 9 pontról is legyen szó. Ha pedig a másodrendű részük különböző, akkor azoknak 4 metszéspontjuk lehet a 10-ből, de a maradék 6 pont nem eshet egy egyenesre. Tehát a két harmadrendű görbe megegyezik, és ezzel beláttuk, hogy $S\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)=S\left(E\mathrm{,}B\mathrm{,}C\mathrm{,}F\right)$.   Komplex függvénytan Eddigi példáinkon valahányszor egy kör és egy egyenes volt az ekvioptikus görbe, az egyenes átment a kör középpontján. Megmutatjuk, hogy ez szükségszerű, sőt, bizonyítást adunk egy sokkal általánosabb állításra, melynek az a következménye, hogy ha az ekvioptikus görbe ``egyszeresen önátmetsző'', akkor ebben a pontban a görbe két érintője merőleges egymásra. Ehhez az ekvioptikus problémát egy újabb szemszögből közelítjük meg: dolgozzunk a komplex számsíkon. Komplex függvénytannal kapcsolatban ajánljuk az olvasónak Szőkefalvi Nagy Béla klasszikus művét: [4]. Legyen $f:\text{C}\to \text{C}$ tetszőleges komplex függvény, és legyen $\begin{array}{c}{\displaystyle R\left(f\right)=\left\{z\mid z\in \text{C}\mathrm{,}f\left(z\right)\in \text{R}\right\}}\end{array}$ azon pontok halmaza, ahol $f$ valós értéket vesz fel. Amennyiben az $A$, $B$, $C$, $D$ pontok a komplex számsíkon az $a$, $b$, $c$, $d$ komplex számoknak felelnek meg, úgy tekintsük az $\begin{array}{c}{\displaystyle f\left(z\right)=\frac{\frac{z-a}{z-b}}{\frac{z-c}{z-d}}=\frac{\left(z-a\right)\left(z-d\right)}{\left(z-b\right)\left(z-c\right)}}\end{array}$ függvényt. Legyen a $z$ számnak megfelelő pont $P$, ekkor $f\left(z\right)$ pontosan azon $z$ értékekre lesz valós, melyekre $\begin{array}{c}{\displaystyle 0\equiv \text{arg}f\left(z\right)\equiv \text{arg}\frac{z-a}{z-b}-\text{arg}\frac{z-c}{z-d}\equiv APB\sphericalangle -CPD\sphericalangle \left(\text{mod}{180}^{\circ }\right)\mathrm{.}}\end{array}$ Így ebben az esetben az ekvioptikus görbéhez jutottunk, $R\left(f\right)=S\left(A\mathrm{,}B\mathrm{,}C\mathrm{,}D\right)$.   A görbe $z_0$ pontját $n$-szeres szinguláris pontnak hívjuk ($n\ge 2$), ha az $f\text{'}\left(z_0\right)$, $f\text{'}\text{'}\left(z_0\right)$, $f\text{'}\text{'}\text{'}\left(z_0\right)$, $\text{...}$ deriváltak közül az $n$-edik, $f^{\left(n\right)}\left(z_0\right)$ az első, amely nem nulla. Ez egy görbén általában úgy jelenik meg szemléletesen, hogy a $z_0$ pontban a görbe $n$-szer ``átmetszi saját magát''. A legtöbb egyenes általában $m$ különböző pontban metsz egy $m$-edrendű görbét, az $n$-szeres szinguláris ponton áthaladó egyenesek azonban csak $\left(m-n+1\right)$ pontban.   5. állítás. Ha egy $f$ (akárhányszor differenciálható) komplex függvény $R\left(f\right)$ görbéjén van egy $n$-szeres szinguláris pont, akkor az ottani $n$ érintő közül a szomszédosak mind ugyanakkora, $\frac{{180}^{\circ }}{n}$ szöget zárnak be.   Bizonyítás. Írjuk fel $f$ Taylor-sorát a $z_0$ pontban: $\begin{array}{c}{\displaystyle f\left(z\right)=f\left(z_0\right)+f\text{'}\left(z_0\right)\cdot \left(z-z_0\right)+\frac{f\text{'}\text{'}\left(z_0\right)}{2}\cdot {\left(z-z_0\right)}^2+\frac{f\text{'}\text{'}\text{'}\left(z_0\right)}{3!}\cdot {\left(z-z_0\right)}^3+\text{...}\mathrm{.}}\end{array}$ Ha az első $\left(n-1\right)$ derivált értéke $z_0$-ban nulla, akkor a függvény $\begin{array}{c}{\displaystyle e\left(z\right)=f\left(z_0\right)+\frac{f^{\left(n\right)}\left(z_0\right)}{n!}\cdot {\left(z-z_0\right)}^n}\end{array}$ közelítése alapján kapott $R\left(e\right)$ halmaz a $z_0$-beli érintők egyenletét adja meg. Mivel $f\left(z_0\right)$ valós, pontosan akkor kapunk $e\left(z\right)$-re is valós értéket, ha ${\displaystyle \begin{array}{c}\hfill {\displaystyle 0\equiv \text{arg}\left(\frac{f^{\left(n\right)}\left(z_0\right)}{n!}\cdot {\left(z-z_0\right)}^n\right)\equiv \text{arg}\frac{f^{\left(n\right)}\left(z_0\right)}{n!}+n\cdot \text{arg}\left(z-z_0\right)\left(\text{mod}{180}^{\circ }\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{arg}\left(z-z_0\right)=-\frac{1}{n}\text{arg}\frac{f^{\left(n\right)}\left(z_0\right)}{n!}+k\cdot \frac{{180}^{\circ }}{n}}\hfill \end{array}}$ valamely $k$ egész számra. Tehát valóban, a $z_0$-beli érintők $z$ pontjaira adódó lehetséges $\left(z-z_0\right)$ komplex számok szögei közül a szomszédosak különbsége mindig $\frac{{180}^{\circ }}{n}$.   Ezzel megmutattuk, hogy ha egy ekvioptikus görbe tartalmaz kétszeres szinguláris pontot, akkor a görbe ebben a pontban merőlegesen metszi önmagát.   Feladatok Végezetül néhány gyakorló feladat:   1. feladat. Adott egy egyenesen négy pont $A$, $B$, $C$, $D$ sorrendben. Mi azon pontok mértani helye, melyekből az $AB$ és $CD$ szakaszok ugyanakkora szögben látszanak?   2. feladat. Az $ABCD$ paralelogramma síkjában fekvő $E$ pontra teljesül, hogy $AEB\sphericalangle \equiv DEC\sphericalangle \left(\text{mod}{180}^{\circ }\right)$. $a)$ Bizonyítsuk be, hogy $BAE\sphericalangle \equiv ECB\sphericalangle \left(\text{mod}{180}^{\circ }\right)$. $b)$ Határozzuk meg az ilyen tulajdonságú $E$ pontok halmazát.   3. feladat. Az $ABC$ háromszög $A$, $B$, $C$ csúcsaiból kiinduló belső szögfelezők a szemközti oldalakat az $E$, $F$, $G$ pontokban metszik. $EF$ és $CG$ metszéspontja $P$, $EG$ és $BF$ metszéspontja $Q$. Bizonyítsuk be, hogy $BAQ\sphericalangle =PAC\sphericalangle$.   4. feladat (IMO 2014/3. nyomán). Adott egy $ABCD$ deltoid, melynek $AC$ a szimmetriatengelye, és egy $P$ pont úgy, hogy a $B$, $D$ pontok az $APC$ szögtartományban vannak, és $APD\sphericalangle =BPC\sphericalangle$. Bizonyítsuk be, hogy a $PAB$ és $PCB$ szögek belső szögfelezői a $PB$ egyenesen metszik egymást.   5. feladat (Szimmedián-lemma). Az $ABC$ háromszög köréírt körének $B$ és $C$-beli érintői $E$-ben metszik egymást. A háromszög $A$ oldalához tartozó súlyvonalat tükrözzük az $A$-ból kiinduló belső szögfelezőre (ezt hívjuk szimmediánnak). Bizonyítsuk be, hogy $E$ rajta van az így kapott egyenesen.   6. feladat (KöMaL, A. 632.). Legyen $ABCD$ konvex négyszög. Az $ABC$ háromszögben legyen $I$ és $J$ a beírt kör, illetve az $A$ csúccsal szemközti hozzáírt kör középpontja. Az $ACD$ háromszögben legyen $K$, illetve $L$ a beírt, illetve az $A$ csúccsal szemközti hozzáírt kör középpontja. Mutassuk meg, hogy az $IL$ és $JK$ egyenesek, valamint a $BCD\sphericalangle$ szögfelezője egy ponton mennek át.   Köszönetnyilvánítás Szeretnék köszönetet mondani Hraskó András tanár úrnak áldozatos munkájáért, észrevételeiért, és mindennemű támogatásáért. Köszönöm matematikatanáraimnak, Dobos Sándor, Kiss Gergely, Gyenes Zoltán, Surányi László, Pósa Lajos tanár uraknak az elmúlt évek során nyújtott kiemelkedő munkájukat. Köszönetet mondok továbbá minden más ismerősömnek, akik biztatásukkal segítették e cikk létrejöttét.   Hivatkozások [1] Hajós György, Bevezetés a geometriába, 44. fejezet (projektív sík, kettősviszony), Tankönyvkiadó, 1971. [2] Horvay Katalin, Reiman István, Projektív geometria, Tankönyvkiadó, 1980. [3] Dobos Sándor, Hraskó András, Projektív geometria, fejezet a Matkönyv, Geometria 11‐12. évfolyam kötetben, http://matkonyv.fazekas.hu/cache/pdf/vol_geometria_iii.pdf [4] Szőkefalvi Nagy Béla, Komplex függvénytan, Polygon jegyzet, 2009.