Cím:	Megoldásvázlatok a 2015/3. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Sztranyák Attila
Füzet:	2015/április, 196 - 202. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. A Bergengóc ötvösök kétféle fémből készítik ékszereiket. A holdfém sűrűsége $5000{\text{kg/m}}^3$, beszerzési ára 1000 ft/g $($a ,,ft'' a Bergengóc fizetőeszköz, a fémtallér rövidítése$)$. A napfém sűrűsége $6000{\text{kg/m}}^3$, beszerzési ára 2000 ft/g. A fémekből kétféle ötvözetet készítenek. Az első ötvözet $1{\text{cm}}^3$-éhez $0\mathrm{,}6{\text{cm}}^3$ holdfémet és $0\mathrm{,}4{\text{cm}}^3$ napfémet használnak fel, míg a második ötvözet $1{\text{cm}}^3$-éhez $0\mathrm{,}4{\text{cm}}^3$ holdfémet és $0\mathrm{,}6{\text{cm}}^3$ napfémet használnak fel $($az ötvözés során nem kell anyagveszteséggel számolni$)$. $a)$ Mennyi a kétféle ötvözet grammonkénti anyagköltsége? Az elkészült ékszerek árát úgy kalkulálják, hogy az ékszer grammban adott tömegét megszorozzák az adott ötvözet grammonkénti anyagköltségével, és erre tesznek még rá $20\%$-ot. $b)$ Mennyi annak az ötvösnek a haszna, aki a 6,3 grammos első ötvözetből álló nyakláncot tévedésből úgy adja el, mintha a második ötvözetből készült volna?  (11 pont)   Megoldás. $a)$ A kétféle fém cm${}^3$-enkénti anyagköltsége: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a_1}& {\displaystyle =1000\left(\frac{\text{ft}}{\text{g}}\right)\cdot 5\left(\frac{\text{g}}{{\text{cm}}^3}\right)=5000\left(\frac{\text{ft}}{{\text{cm}}^3}\right)\text{és}}\hfill \\ \hfill {\displaystyle a_2}& {\displaystyle =2000\left(\frac{\text{ft}}{\text{g}}\right)\cdot 6\left(\frac{\text{g}}{{\text{cm}}^3}\right)=12000\left(\frac{\text{ft}}{{\text{cm}}^3}\right)\mathrm{.}}\hfill \end{array}}$ A két ötvözet cm${}^3$-enkénti tömege és anyagköltsége: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle m_1}& {\displaystyle =0\mathrm{,}6\left({\text{cm}}^3\right)\cdot 5\left(\frac{\text{g}}{{\text{cm}}^3}\right)+0\mathrm{,}4\left({\text{cm}}^3\right)\cdot 6\left(\frac{\text{g}}{{\text{cm}}^3}\right)=5\mathrm{,}4\text{g}\text{és}}\hfill \\ \hfill {\displaystyle k_1}& {\displaystyle =0\mathrm{,}6\left({\text{cm}}^3\right)\cdot 5000\left(\frac{\text{ft}}{\text{g}}\right)+0\mathrm{,}4\left({\text{cm}}^3\right)\cdot 12000\left(\frac{\text{ft}}{\text{g}}\right)=7800\text{ft}\mathrm{,}\text{illetve}}\hfill \\ \hfill {\displaystyle m_2}& {\displaystyle =0\mathrm{,}4\left({\text{cm}}^3\right)\cdot 5\left(\frac{\text{ft}}{\text{g}}\right)+0\mathrm{,}6\left({\text{cm}}^3\right)\cdot 6\left(\frac{\text{ft}}{\text{g}}\right)=5\mathrm{,}6\text{g}\text{és}}\hfill \\ \hfill {\displaystyle k_2}& {\displaystyle =0\mathrm{,}4\left({\text{cm}}^3\right)\cdot 5000\left(\frac{\text{ft}}{\text{g}}\right)+0\mathrm{,}6\left({\text{cm}}^3\right)\cdot 12000\left(\frac{\text{ft}}{\text{g}}\right)=9200\text{ft}\mathrm{.}}\hfill \end{array}}$ Így a grammonkénti anyagköltségek: $\begin{array}{c}{\displaystyle k_{\text{1g}}=\frac{7800\text{ft}}{5\mathrm{,}4\text{g}}\approx 1444\mathrm{,}4\frac{\text{ft}}{\text{g}}\mathrm{,}\text{és}{k}_{\text{2g}}=\frac{9200\text{ft}}{5\mathrm{,}6\text{g}}\approx 1642\mathrm{,}9\frac{\text{ft}}{\text{g}}\mathrm{.}}\end{array}$ $b)$ 6,3 gramm anyagköltsége az első ötvözetből: $\begin{array}{c}{\displaystyle \frac{7800\text{ft}}{5\mathrm{,}4\text{g}}\cdot 6\mathrm{,}3\text{g=9100 ft. }}\end{array}$ A nyaklánc eladási ára: $\begin{array}{c}{\displaystyle \frac{9200\text{ft}}{5\mathrm{,}6\text{g}}\cdot 6\mathrm{,}3\text{g <math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math>1,2= 12 420 ft. }}\end{array}$ Így az ötvös haszna: $12420-9100=3320$ ft.   2. Hány olyan $($egybevágóságtól eltekintve$)$ különböző téglalap van, melynek oldalai $($cm-ben$)$ egész számok, míg területe és kerülete $({\text{cm}}^2$-ben és cm-ben$)$ $100$-nál nem nagyobb négyzetszám?  (12 pont)   Megoldás. A téglalap oldalai: $a\le b$, így $a\le 10$. A területre és a kerületre: $a\cdot b=n^2\le 100$ és $2\left(a+b\right)=k^2\le 100$, így $nk\le 10$. I. Ha $a=b$, akkor a téglalap négyzet, így a terület mindig négyzetszám, a kerület pedig $4a=k^2$ miatt pontosan akkor négyzetszám, ha $a=b$ négyzetszám. Vagyis az $1\times 1$-es, $4\times 4$-es, $9\times 9$-es téglalap megfelelő. II. Ha $a<b$, akkor $a\le 9$ is teljesül. Az esetet két részre osztjuk: II.1. Ha $a=1$, akkor $b=n^2$, és a kerületből $2+2n^2=k^2$. Mivel ekkor $k$ páros négyzetszám, így 4-gyel is osztható, de ez csak akkor lehet, ha $n$ páratlan. A lehetséges eseteket ($n=\mathrm{3,5,7,9}$) végigpróbálva csak $n=7$ ad jó megoldást. Ekkor $a=1$, $b=7^2=49$, vagyis az $1\times 49$-es téglalap is jó. II.2. Ha $1<a<b$, akkor $a$ az $n^2$-nek egy $n$-nél kisebb pozitív osztója és $b=\frac{n^2}{a}$. Ez az $a$ érték az $n=\mathrm{2,3,5,7}$ prímek esetén csak $a=1$ lehet, ezt pedig már megvizsgáltuk. Nézzük végig a többi esetet is: ${\displaystyle \begin{array}{cc}{\displaystyle \text{ Ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi><mo stretchy="false">=</mo><mn>4</mn></math>: }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo stretchy="false">=</mo><mn>2</mn></math> esetén <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>a</mi><mo stretchy="false">+</mo><mi>b</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>2</mn><mo stretchy="false">+</mo><mn>8</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>20</mn><mo>≠</mo><mrow><msup><mrow><mi>k</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>.}}\hfill \\ {\displaystyle \text{ Ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi><mo stretchy="false">=</mo><mn>6</mn></math>: }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo stretchy="false">=</mo><mn>2</mn></math> esetén <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>a</mi><mo stretchy="false">+</mo><mi>b</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>2</mn><mo stretchy="false">+</mo><mn>18</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>40</mn><mo>≠</mo><mrow><msup><mrow><mi>k</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>, míg}}\hfill \\ {\displaystyle }\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo stretchy="false">=</mo><mn>3</mn></math> esetén <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>a</mi><mo stretchy="false">+</mo><mi>b</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>3</mn><mo stretchy="false">+</mo><mn>12</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>30</mn><mo>≠</mo><mrow><msup><mrow><mi>k</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>, míg}}\hfill \\ {\displaystyle }\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo stretchy="false">=</mo><mn>4</mn></math> esetén <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>a</mi><mo stretchy="false">+</mo><mi>b</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>4</mn><mo stretchy="false">+</mo><mn>9</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>26</mn><mo>≠</mo><mrow><msup><mrow><mi>k</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>.}}\hfill \\ {\displaystyle \text{ Ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi><mo stretchy="false">=</mo><mn>8</mn></math>: }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo stretchy="false">=</mo><mn>2</mn></math> esetén <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>a</mi><mo stretchy="false">+</mo><mi>b</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>2</mn><mo stretchy="false">+</mo><mn>32</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>68</mn><mo>≠</mo><mrow><msup><mrow><mi>k</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>, míg}}\hfill \\ {\displaystyle }\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo stretchy="false">=</mo><mn>4</mn></math> esetén <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>a</mi><mo stretchy="false">+</mo><mi>b</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>4</mn><mo stretchy="false">+</mo><mn>16</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>40</mn><mo>≠</mo><mrow><msup><mrow><mi>k</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>.}}\hfill \\ {\displaystyle \text{ Ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi><mo stretchy="false">=</mo><mn>9</mn></math>: }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo stretchy="false">=</mo><mn>3</mn></math> esetén <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>a</mi><mo stretchy="false">+</mo><mi>b</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>3</mn><mo stretchy="false">+</mo><mn>27</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>60</mn><mo>≠</mo><mrow><msup><mrow><mi>k</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>.}}\hfill \\ {\displaystyle \text{ Ha <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi><mo stretchy="false">=</mo><mn>10</mn></math>: }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo stretchy="false">=</mo><mn>2</mn></math> esetén <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>a</mi><mo stretchy="false">+</mo><mi>b</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>2</mn><mo stretchy="false">+</mo><mn>50</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>104</mn><mo stretchy="false">></mo><mn>100</mn></math>, míg}}\hfill \\ {\displaystyle }\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo stretchy="false">=</mo><mn>4</mn></math> esetén <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>a</mi><mo stretchy="false">+</mo><mi>b</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>4</mn><mo stretchy="false">+</mo><mn>25</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>58</mn><mo>≠</mo><mrow><msup><mrow><mi>k</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>, míg}}\hfill \\ {\displaystyle }\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mo stretchy="false">=</mo><mn>5</mn></math> esetén <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>a</mi><mo stretchy="false">+</mo><mi>b</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>2</mn><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>5</mn><mo stretchy="false">+</mo><mn>20</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mn>50</mn><mo>≠</mo><mrow><msup><mrow><mi>k</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>. }}\hfill \end{array}}$ Vagyis összesen négy ilyen téglalap van, ezek méretei: $1\times 1$, $4\times 4$, $9\times 9$, és $1\times 49$.   3. Oldjuk meg a következő egyenleteket a valós számok halmazán: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle a)}& {\displaystyle \text{log}{}_4\left(x+1\right)+\text{log}{}_4\left(x+2\right)=\text{log}{}_2\sqrt[]{6}\mathrm{,}}\hfill \\ \hfill {\displaystyle b)}& {\displaystyle {\displaystyle \frac{2x^2-3x+1}{x^2-3x+2}}-{\displaystyle \frac{2x^2-2x-12}{x^2-7x+12}}=1.}\hfill \end{array}}}\end{array}$ (14 pont)   Megoldás. A logaritmus definíciója miatt az $x+1>0$ feltételnek teljesülnie kell, amiből $x>-1$. Használva a logaritmus azonosságait, a jobb oldalt is 4-es alapra alakítva: $\begin{array}{c}{\displaystyle \text{log}{}_4\left(\left(x+1\right)\left(x+2\right)\right)=\text{log}{}_{4}6.}\end{array}$ Mivel a logaritmus-függvény szigorúan monoton függvény, innen $\left(x+1\right)\left(x+2\right)=6$, és így $x^2+3x-4=0$, amiből $x_1=1$ és $x_2=-4$ adódik. Ezek közül csak az első megoldás megfelelő, vagyis az egyenlet megoldása: $x=1$. $b)$ A törtek számlálóit és nevezőit szorzattá alakítva: $\begin{array}{c}{\displaystyle \frac{\left(2x-1\right)\left(x-1\right)}{\left(x-1\right)\left(x-2\right)}-\frac{\left(2x+4\right)\left(x-3\right)}{\left(x-3\right)\left(x-4\right)}=1.}\end{array}$ Innen $x\notin \left\{1;2;3;4\right\}$. Egyszerűsítve a törteket, majd a maradék nevezőkkel szorozva: $\begin{array}{c}{\displaystyle \left(2x-1\right)\left(x-4\right)-\left(2x+4\right)\left(x-2\right)=\left(x-2\right)\left(x-4\right)\mathrm{.}}\end{array}$ Elvégezve a zárójelfelbontásokat: $\begin{array}{c}{\displaystyle 2x^2-9x+4-2x^2+8=x^2-6x+\mathrm{8,}}\end{array}$ innen $x^2+3x-4=0$, amiből $x_1=1$ és $x_2=-4$ adódik. Ezek közül csak a második megoldás megfelelő, vagyis az egyenlet megoldása: $x=-4$.   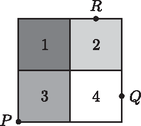4. Peti tíz egyforma $2$ egység élű építőkockából tornyot épít. A torony alapja $4\text{cm<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>×</mo></math>4 cm}$-es négyzet, de az egyes részeinek más-más a magassága. $($A felülnézeti ábra azt mutatja, hogy egy-egy rész hány darab $2\times 2\times 2$ cm-es kockából áll.$)$     Az ábrán látható $P$, $Q$, $R$ pontok az egyes részek legmagasabban lévő építőkockáinak a felső lapján vannak. $P$ az egyik négyzetlap csúcsa, míg $Q$ és $R$ a felső négyzetlapok megfelelő éleinek felezőpontjai. $a)$ Mekkora a $($térbeli$)$ $PQR$ háromszög $P$-nél lévő szöge? $b)$ Peti $4$ piros, $3$ fehér, $2$ zöld és $1$ kék kockából építi meg a fenti tornyot. Hányféle különböző felülnézeti ábra áll így elő? $($A nem identikus egybevágósági transzformációval egymásba vihető ábrákat különbözőnek tekintjük.$)$  (14 pont)   Megoldás. $a)$ Az $a$, $b$, $c$ élhosszú téglatest testátlóinak hossza $d=\sqrt[]{a^2+b^2+c^2}$. A $P$, $Q$, és $R$ pontok között futó térbeli szakaszok tekinthetők a megfelelő téglatestek testátlóinak: $PQ$-nál a téglatest élei 2, 4 és 1; $QR$-nél 3, 4 és 1; $RP$-nél pedig 3, 4 és 2. Ezek alapján a $P$, $Q$, $R$ pontok között lévő távolságok: $\begin{array}{c}{\displaystyle r=d\left(PQ\right)=\sqrt[]{21}\mathrm{,}p=d\left(QR\right)=\sqrt[]{26}\mathrm{,}q=d\left(RP\right)=\sqrt[]{29}\mathrm{.}}\end{array}$ Koszinusz-tétellel kiszámoljuk a $P$-nél lévő ($p$-vel szemközti) $\gamma$ szöget: $\begin{array}{c}{\displaystyle p^2=q^2+r^2-2qr\text{cos}\gamma \mathrm{,}\text{így}\text{cos}\gamma =\frac{q^2+r^2-p^2}{2qr}=\frac{29+21-26}{2\sqrt[]{29}\sqrt[]{21}}=\frac{12}{\sqrt[]{609}}\mathrm{,}}\end{array}$ amiből $\gamma \approx 60\mathrm{,}{9}^{\circ }$. $b)$ A piros, fehér, zöld, kék színeket P, F, Z, K betűvel jelölve a feladat ekvivalens azzal, hogy 4 db P, 3 db F, 2 db Z és 1 db K betűből hányféle 4 betűs ,,szó'' képezhető. Vizsgáljuk meg a lehetséges eseteket aszerint, hogy a felülnézeti rajzon a színek hogy látszódnak. I. Valamely színből 4 látható. Ekkor a színek száma rendre 4, 0, 0, 0. Mivel csak a P-ből van 4 darab, ezért ez 1 eset. II. Valamely színből 3 látható. A színek száma ekkor 3, 1, 0, 0. Az első szín kettőből (P, F), a második szín háromból választható, vagyis hatféleképpen választhatunk színt. Ha a színeket már kiválasztottuk, a négybetűs szó $\frac{4!}{3!}=4$-féleképpen képezhető. Így itt $6\cdot 4=24$ eset van. III. Valamely színből 2 látható. Ekkor a színek száma 2, 2, 0, 0 vagy 2, 1, 1, 0. Az első esetben a két látható szín háromból (P, F, Z) választható $\left(\genfrac{}{}{0ex}{}{3}{2}\right)=3$-féleképpen. Ha a színeket már kiválasztottuk, a négybetűs szó $\frac{4!}{2!\cdot 2!}=6$-féleképpen képezhető. Így itt $3\cdot 6=18$ eset van. A második esetben az első szín háromból (P, F, Z), a kimaradó (negyedik) szín szintén háromból választható, vagyis a színeket kilencféleképpen választhatjuk. Ha a színeket már kiválasztottuk, a négybetűs szó $\frac{4!}{2!}=12$-féleképpen képezhető, így itt $9\cdot 12=108$ eset van. IV. Végül, ha minden színből 1 látható, akkor nyilván $4!=24$ eset van. Vagyis összesen $1+24+18+108+24=175$-féle felülnézeti ábra van.   II. rész     5. $a)$ Igazoljuk, hogy a következő két sorozat konvergens, és közös a határértékük: $\begin{array}{c}{\displaystyle a_n=\frac{6n^2-n-1}{2n^2+n+1}\mathrm{,}{b}_n=\sqrt[]{n^2+6n+12}-n\mathrm{.}}\end{array}$ $b)$ Igazoljuk, hogy a fenti $a_n$ sorozat minden tagja kisebb a fenti $b_n$ sorozat valamennyi tagjánál.  (16 pont)   Megoldás. $a)$ A számláló és a nevező minden tagját osztva $n^2$-tel: $\begin{array}{c}{\displaystyle a_n=\frac{6n^2-n-1}{2n^2+n+1}=\frac{6-\frac{1}{n}-\frac{1}{n^2}}{2+\frac{1}{n}+\frac{1}{n^2}}\mathrm{.}}\end{array}$ Mind a számlálóban, mind a nevezőben az első tagok kivételével nullsorozatról van szó, így $a_n\to \frac{6}{2}=3$. A másik sorozatot a konjugáltjával bővítve: $\begin{array}{c}{\displaystyle b_n=\frac{\left(\sqrt[]{n^2+6n+12}-n\right)\left(\sqrt[]{n^2+6n+12}+n\right)}{\sqrt[]{n^2+6n+12}+n}\mathrm{.}}\end{array}$ Innen: $\begin{array}{c}{\displaystyle b_n=\frac{6n+12}{\sqrt[]{n^2+6n+12}+n}=\frac{6+\frac{12}{n}}{\sqrt[]{1+\frac{6}{n}+\frac{12}{n^2}}+1}\to \frac{6}{1+1}=3.}\end{array}$ $b)$ Az első sorozatnál mind a számláló, mind a nevező mindig pozitív, és mivel $\begin{array}{c}{\displaystyle 6n^2-n-1<6n^2+3n+3=3\left(2n^2+n+1\right)\mathrm{,}}\end{array}$ azért $a_n<3$ minden $n$-re. A második sorozatnál $\begin{array}{c}{\displaystyle b_n=\sqrt[]{n^2+6n+12}-n>\sqrt[]{n^2+6n+9}-n=\left(n+3\right)-n=3.}\end{array}$ Mivel a közös határértéknél az $a_n$ sorozat minden tagja kisebb, míg a $b_n$ sorozat minden tagja nagyobb, igazoltuk a $b)$ pontot is.   6. A térbeli derékszögű-koordináta-rendszerben felveszünk $3$ piros pontot: $A\left(1;0;0\right)$, $B\left(2;0;0\right)$, és $C\left(3;0;0\right)$, valamint $3$ fehér pontot: $D\left(0;1;0\right)$, $E\left(0;2;0\right)$, és $F\left(0;3;0\right)$, valamint 3 zöld pontot: $G\left(0;0;1\right)$, $H\left(0;0;2\right)$, és $I\left(0;0;3\right)$. $a)$ Véletlenszerűen kiválasztunk a kilenc pont közül hármat úgy, hogy a kiválasztott pontok egy háromszög csúcsai legyenek. Mekkora a valószínűsége annak, hogy az így kapott háromszögnek vannak azonos színű csúcsai? $b)$ A kilenc pont közül válasszunk ki úgy néhányat, hogy az általuk meghatározott test térfogata a lehető legnagyobb legyen. Mely csúcsokat válasszuk ki, és mekkora lesz ekkor a kérdéses térfogat?  (16 pont)   Megoldás. $a)$ Akkor van (nem elfajuló) háromszög, ha a kiválasztott három pont nincs egy egyenesen. Ez csak három esetben ($ABC$, $DEF$, valamint $GHI$ választása esetén) nem teljesül. Mivel 9 pont közül hármat $\left(\genfrac{}{}{0ex}{}{9}{3}\right)=84$-féleképp választhatunk ki, azért összesen $84-3=81$ olyan háromszög van, melyek csúcsai a 9 csúcs közül kerülnek ki. Ezek közül rosszak azok, melyeknek három különböző színű csúcsa van. Ezek száma $3^3=27$. Így összesen $81-27=54$ olyan háromszög van, melynek vannak azonos színű csúcsai, így a kérdéses valószínűség: $\frac{54}{81}=\frac{2}{3}$. $b)$ Mivel az $ACDFGI$ test az összes többi testet tartalmazza, a kérdéses test ez a csonka gúla. A térfogata legegyszerűbben úgy számolható ki, hogy az $OCFI$ gúla térfogatából kivonjuk az $OADG$ gúla térfogatát (az $O$ pont az origó). A térfogat így: $\begin{array}{c}{\displaystyle V=\frac{3^3}{6}-\frac{1^3}{6}=\frac{26}{6}=\frac{13}{3}\mathrm{.}}\end{array}$ Vagyis a térfogat: $\frac{13}{3}$.   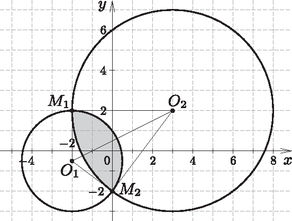7. Tekintsük a derékszögű koordináta-rendszerben a következő két kört: $\begin{array}{c}{\displaystyle k_1:x^2+4x+y^2+y=2\text{és}{k}_2:x^2-6x+y^2-4y=12.}\end{array}$ Mekkora annak a síkrésznek a területe, amelyet mind a két kör lefed?  (16 pont)   Megoldás. A körök középpontjainak és sugarainak kiszámításához átalakítjuk az egyenleteket. Jelölje a $k_1$ és a $k_2$ kör sugarát, illetve középpontját rendre $r_1$ és $r_2$, illetve $O_1$ és $O_2$. A $k_1$ kör esetén $\begin{array}{c}{\displaystyle {\left(x+2\right)}^2+{\left(y+\frac{1}{2}\right)}^2=\frac{25}{4}={\left(\frac{5}{2}\right)}^2\mathrm{,}}\end{array}$ azaz $O_1\left(-2;-\frac{1}{2}\right)$, $r_1=\frac{5}{2}$.     A $k_2$ kör esetén ${\left(x-3\right)}^2+{\left(y-2\right)}^2=25$, azaz $O_2\left(3;2\right)$, $r_2=5$. Az első kör egyenletéből kivonva a második körét: $\begin{array}{c}{\displaystyle 10x+5y=-\mathrm{10,}\text{amiből}y=-2x-2.}\end{array}$ Ezt behelyettesítve mondjuk az első egyenletbe: $x^2+4x+\left(-2x-2\right)\left(-2x-1\right)=2$, amiből $x^2+4x+4x^2+6x+2=2$, vagyis $5x^2+10x=0$, tehát $x_1=-2$ és $x_2=0$ adódik. Innen (behelyettesítéssel) a két kör metszéspontjai: $M_1\left(-2;2\right)$, és $M_2\left(0;-2\right)$. Mivel $\begin{array}{c}{\displaystyle d\left(O_1{O}_2\right)=\sqrt[]{5^2+{\left(\frac{5}{2}\right)}^2}=\sqrt[]{\frac{125}{4}}\mathrm{,}d\left(O_1{M}_2\right)=\sqrt[]{2^2+{\left(\frac{3}{2}\right)}^2}=\sqrt[]{\frac{25}{4}}=\frac{5}{2}\mathrm{,}}\end{array}$ és $\begin{array}{c}{\displaystyle d\left(O_2{M}_2\right)=\sqrt[]{3^2+4^2}=5=\sqrt[]{25}=\sqrt[]{\frac{100}{4}}\mathrm{,}}\end{array}$ emiatt (a Pitagorasz-tétel megfordítása szerint) az $O_1{M}_2{O}_2\sphericalangle$ derékszög. Innen az $M_2{O}_1{M}_1$ szöget $\alpha$-val, az $M_1{O}_2{M}_2$ szöget $\beta$-val jelölve: $\begin{array}{c}{\displaystyle \text{cos}\frac{\alpha }{2}=\frac{\sqrt[]{\frac{25}{4}}}{\sqrt[]{\frac{125}{4}}}=\frac{1}{\sqrt[]{5}}\mathrm{,}\text{amiből}\alpha \approx 126\mathrm{,}{87}^{\circ }\mathrm{,}}\end{array}$ és innen $\beta \approx 53\mathrm{,}{13}^{\circ }$. A kérdéses metszet területének kiszámításához az $O_1$ középpontú $M_2{M}_1$ ívhez tartozó körcikk területét és az $O_2$ középpontú $M_1{M}_2$ ívhez tartozó körcikk területét összeadjuk, és ebből kivonjuk az $O_1{M}_1{O}_2{M}_2$ derékszögű deltoid területét, melynek oldalai 5 és 2,5 egység hosszúak. Vagyis a metszet területe: $\begin{array}{c}{\displaystyle T\approx \frac{2\mathrm{,}{5}^2\cdot \pi \cdot {126\mathrm{,}87}^{\circ }}{{360}^{\circ }}+\frac{5^2\cdot \pi \cdot {53\mathrm{,}13}^{\circ }}{{360}^{\circ }}-5\cdot \frac{5}{2}\approx 6\mathrm{,}01.}\end{array}$ A két kör által közösen lefedett síkrész területe: $T\approx 6\mathrm{,}01$.   8. A $p$ paraméter mely értékeire lesz a $\begin{array}{c}{\displaystyle p{x}^2-\left(p-1\right)x-\frac{3}{4}p+\frac{1}{2}=0}\end{array}$ $a)$ egyenletnek egy megoldása; $b)$ egyenletnek két megoldása, az egyik pozitív, a másik negatív; $c)$ egyenletnek gyöke a $-3;$ $d)$ egyenlet gyökeinek az aránya $1:2?$  (16 pont)   Megoldás. $a)$ Ha $p=0$ (vagyis az egyenlet elsőfokú), akkor $x=-\frac{1}{2}$ (ekkor egy megoldás van.) Különben az egyenlet másodfokú, és egy megoldása pontosan akkor van, ha az egyenlet diszkriminánsa 0: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle D}& {\displaystyle ={\left(p-1\right)}^2-4\cdot p\cdot \left(-\frac{3}{4}p+\frac{1}{2}\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =p^2-2p+1+3p^2-2p=4p^2-4p+1={\left(2p-1\right)}^2=0.}\hfill \end{array}}$ Innen $p=\frac{1}{2}$. Vagyis $p=0$, és $p=\frac{1}{2}$ esetén van az egyenletnek egy megoldása. A $b)$‐$c)$‐$d)$ pontok nem teljesülhetnek $p=0$ esetén. Így a továbbiakban $p\ne 0$. Mivel $D$ ,,szép'', adjuk meg a $p$ segítségével az egyenlet két megoldását: $\begin{array}{c}{\displaystyle x_{\mathrm{1,2}}=\frac{p-1\pm |2p-1|}{2p}\mathrm{,}\text{innen}{x}_1=\frac{3p-2}{2p}\mathrm{,}{x}_2=\frac{-p}{2p}=-\frac{1}{2}\mathrm{.}}\end{array}$ Innen egyszerűen adódnak a válaszok: $b)$ Mivel a negatív gyök megvan, így $\frac{3p-2}{2p}>0$, és ebből $p>\frac{2}{3}$, vagy $p<0$. $c)$ $-3=\frac{3p-2}{2p}$, innen $p=\frac{2}{9}$. $d)$ Itt két eset van aszerint, hogy melyik gyök a nagyobb. Vagy $-1=\frac{3p-2}{2p}$, és így $p=\frac{2}{5}$, vagy $-\frac{1}{4}=\frac{3p-2}{2p}$, és így $p=\frac{4}{7}$.   9. Kati ,,peches''-számai a $3$-as, és a $7$-es. Egy nap $1$-től kezdve elkezdte felírni a pozitív egészeket, de azokat a számokat, amikben volt hármas, vagy hetes jegy kihagyta. $a)$ Milyen számjegyekből áll a Kati által felírt $2015$-dik szám? $b)$ Hanyadik számként írta fel Kati a $2015$-ös számot?  (16 pont)   Megoldás. Használjunk 8-as számrendszert. A Kati által felírt számok tekinthetők 8-as számrendszerbeli számoknak, csak jól el kell készítenünk a két számrendszer (a ,,rendes 8-as számrendszer'', és Katié) közötti ,,kódtáblát''. Ez a tábla a következő:   ${\displaystyle \begin{array}{|ccccccccc|}\hline {\displaystyle \text{8-as számrendszerben}}\hfill & {\displaystyle \text{ 0}}\hfill & {\displaystyle \text{ 1}}\hfill & {\displaystyle \text{ 2}}\hfill & {\displaystyle \text{ 3}}\hfill & {\displaystyle \text{ 4}}\hfill & {\displaystyle \text{ 5}}\hfill & {\displaystyle \text{ 6}}\hfill & {\displaystyle \text{ 7 }}\hfill \\ {\displaystyle \text{Katinál}}\hfill & {\displaystyle \text{ 0}}\hfill & {\displaystyle \text{ 1}}\hfill & {\displaystyle \text{ 2}}\hfill & {\displaystyle \text{ 4}}\hfill & {\displaystyle \text{ 5}}\hfill & {\displaystyle \text{ 6}}\hfill & {\displaystyle \text{ 8}}\hfill & {\displaystyle \text{ 9 }}\hfill \\ \hline\end{array}}$   Vagyis pl. a 8-as számrendszerbeli 53 megegyezik a Kati-féle 64 alakú számmal. Ezt a továbbiakban ${53}_8={64}_K$-ként fogjuk jelölni. $a)$ A 8-as számrendszerben a 2015-dik számot pl. ismételt 8-cal való maradékos osztásokkal meghatározhatjuk: $\begin{array}{c}{\displaystyle 2015=251\cdot 8+\mathrm{7,}251=31\cdot 8+\mathrm{3,}31=3\cdot 8+\mathrm{7,}3=0\cdot 8+3.}\end{array}$ Vagyis ${2015}_{10}={3737}_8$. Mivel ${3737}_8={4949}_K$, ezért a Kati listáján szereplő 2015-dik szám a 4949. $b)$ Mivel ${2015}_K={2014}_8=2\cdot 8^3+0\cdot 8^2+1\cdot 8^1+4={1036}_{10}$, ezért Kati a 2015-t a saját listáján az 1036-dik számként írta fel.