Cím:	Emelt szintű gyakorló feladatsor
Szerző(k):	Loránt László
Füzet:	2015/április, 194 - 195. oldal	PDF  |  MathML

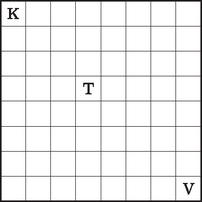
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Bizonyítsuk be, hogy $\text{lg}2$ irracionális.  (11 pont)   2. $a)$ Hány különböző útvonalon juthatunk el a $8\times 8$-as sakktáblán a bal felső sarokban lévő, az ábrán K-val jelölt mezőről a jobb alsó sarokban lévő, V-vel jelölt mezőre, ha bármely érintett mezőről csak az alatta lévő, vagy a jobb oldalán lévő mezőre léphetünk?     $b)$ Hány olyan útvonal van ezek között, amely a kiinduló mezőtől számított negyedik oszlop és negyedik sor kereszteződésében lévő, T-vel jelölt mezőt nem érinti?  (12 pont)   3. $a)$ Bizonyítsuk be, hogy ha az $\left(a_n\right)$ végtelen számtani sorozat elemei természetes számok és ezek között van köbszám, akkor a sorozatnak végtelen sok köbszám eleme van. $b)$ Ha például a sorozatban szerepel a $125$, és a sorozat differenciája $3$, akkor lehet-e $125$-nél kisebb köbszám a sorozatban?  ($\text{10}+\text{4}$ pont)   4. Bútorok hegyes sarkai sérülést okozhatnak. Különösen kisgyermekekre jelentenek veszélyt egy asztal sarkai. Éppen ezért az $\text{1 m<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>×</mo></math>1 m}$-es asztalunk lapját lekerekítettük az asztallap síkjára merőlegesen tartott fűrésszel olyan körívek mentén, amelyek középpontja egybeesik a négyzet alakú felület középpontjával. A négy oldalél mindegyikéből 80 cm hosszú egyenes szakasz maradt meg. Az egyenletes vastagságú asztallap tömege eredetileg 7 kg volt. Mekkora lett a tömege az átalakítás után?  (14 pont)   II. rész     5. Egy dobókockával kétszer dobunk. $a)$ Hány elemi esemény alkotja az eseményteret? $b)$ Mekkora annak a valószínűsége, hogy a dobott számok összege legalább $9?$ $c)$ Mekkora annak a feltételes valószínűsége, hogy a dobott számok összege legalább $9$, ha az első dobott szám legalább $5?$ $d)$ Mekkora annak a feltételes valószínűsége, hogy a dobott számok összege legalább $9$, ha az első dobott szám legfeljebb $4?$  ($\text{2}+\text{4}+\text{5}+\text{5}$ pont)   6. Az $f\left(x\right)=x^3+a{x}^2+2x$ függvényről tudjuk, hogy inflexiós érintője párhuzamos az $x+y=0$ egyenletű egyenessel. Határozzuk meg az $a$ együttható értékét. Igazoljuk, hogy a függvény inflexiós pontja az $x$-tengelyen van.  (16 pont)   7. Bizonyítsuk be, hogy $\begin{array}{c}{\displaystyle \sqrt[]{\text{sin}x}+\sqrt[]{\text{cos}x}\le \sqrt[4]{8}\mathrm{,}}\end{array}$ ha $0\le x\le \frac{\pi }{2}$.  (16 pont)   8. Szerkesszünk derékszögű háromszöget, ha adott a beírt és a körülírt körének sugara. Mi a megoldhatóság feltétele? (Elegendő a szerkesztés menetét leírni.)  (16 pont)   9. Egy harckocsizó alakulatnál szolgáló férfiak $40$ fős csoportjában a testmagasság $\left(x_i\right)$ és a testtömeg $\left(y_i\right)$ adatait a következő táblázat tartalmazza:   ${\displaystyle \begin{array}{|cc|}\hline \hfill {\displaystyle \text{testmagasság <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>x</mi></mrow><mrow><mi>i</mi></mrow></msub></mrow></math> [cm] }}\hfill & \hfill {\displaystyle \text{ testtömeg <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>y</mi></mrow><mrow><mi>i</mi></mrow></msub></mrow></math> [kg]}}\hfill \\ \hfill {\displaystyle \text{162 }}\hfill & \hfill {\displaystyle \text{ 70, 77}}\hfill \\ \hfill {\displaystyle \text{163 }}\hfill & \hfill {\displaystyle \text{ 61 }}\hfill \\ \hfill {\displaystyle \text{164 }}\hfill & \hfill {\displaystyle \text{ 58, 64, 68}}\hfill \\ \hfill {\displaystyle \text{165 }}\hfill & \hfill {\displaystyle \text{ 73 }}\hfill \\ \hfill {\displaystyle \text{166 }}\hfill & \hfill {\displaystyle \text{ 62, 65, 70}}\hfill \\ \hfill {\displaystyle \text{167 }}\hfill & \hfill {\displaystyle \text{ 65, 66, 75, 80}}\hfill \\ \hfill {\displaystyle \text{168 }}\hfill & \hfill {\displaystyle \text{ 63, 69, 71, 79}}\hfill \\ \hfill {\displaystyle \text{169 }}\hfill & \hfill {\displaystyle \text{ 64, 70, 75, 76}}\hfill \\ \hfill {\displaystyle \text{170 }}\hfill & \hfill {\displaystyle \text{ 58, 61, 71, 75, 75, 88}}\hfill \\ \hfill {\displaystyle \text{171 }}\hfill & \hfill {\displaystyle \text{ 67, 68, 75, 77}}\hfill \\ \hfill {\displaystyle \text{172 }}\hfill & \hfill {\displaystyle \text{ 61, 65, 70, 84}}\hfill \\ \hfill {\displaystyle \text{173 }}\hfill & \hfill {\displaystyle \text{ 58, 77}}\hfill \\ \hfill {\displaystyle \text{174 }}\hfill & \hfill {\displaystyle \text{ 63, 80}}\hfill \\ \hline\end{array}}$   $a)$ Ha a kg-ban mért testtömeget a m-ben mért testmagasság négyzetével elosztjuk, akkor az úgynevezett testtömeg-indexet kapjuk. A katonaorvos egy bizonyos egész számnál nagyobb testtömeg-index esetén minősít valakit túlsúlyosnak. Mekkora ez az érték, ha az orvos szerint a szóbanforgó csoportban a túlsúlyosok aránya $10\%?$ $b)$ Számítsuk ki az $\overline{x}$ és $\overline{y}$ átlagokat. Jelölje $u$ azoknak az $\left(x_i\mathrm{,}{y}_i\right)$ értékpároknak a számát, amelyeknél a két adat az átlaghoz képest ugyanabban az irányban tér el, $v$ pedig azoknak a számát, ahol az eltérés ellentétes irányú. Számítsuk ki az $\frac{u-v}{u+v}$ hányadost. Mire következtethetünk ebből?  ($\text{8}+\text{8}$ pont)