Cím: Matematika és fizika totó megoldása
Füzet: 2017/január, 56 - 58. oldal  PDF  |  MathML 
Hivatkozás(ok):2017/január: Matematika és fizika totó a 2016. évi Őszi KöMaL Ankéton

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A telitalálatos szelvény:

2,1,1,2,X,2,X,2,1,2,2,2,X,2.

A legtöbb (12) találatot Hansel Soma (Szegedi Radnóti M. Kís. Gimn., 12. évf.), Nagy Kartal (az ELTE matematikus hallgatója) és Szemerédi Levente (Szegedi Radnóti M. Kís. Gimn., 11. évf.) érte el.
Az alábbiakban rövid útmutatást adunk a feladatok megoldásához.
 
1. Ha x∉E, akkor x∉D∖E miatt x∉D, majd x∉C∖D miatt x∉C stb., végül x∉A következne, ekkor pedig x∉A∪E. Tehát x∈E biztosan igaz (és az x∉E pedig biztosan hamis).
Legyen A={1}, B={1}, C={1}, D={1}, E={2} és x=2. Ekkor az x∈A; x∈B; x∈C, x∈D és x∉E állítások hamisak.
Legyen A={1}, B={1}, C={1}, D={1}, E={1} és x=1. Ekkor az x∉A; x∉B; x∉C, x∉D és x∉E állítások hamisak.
Tehát egyedül az x∈E állítás az, ami biztosan igaz.
 

2. Az 1950-es években végzett megfigyelések kimutatták, hogy a Vénusz forgása retrográd, vagyis a Föld forgásával (és így a saját keringési irányával is) ellentétes irányú.
 
3. -f(7)=-a⋅77-b⋅73-c⋅7+5=a⋅(-7)7+b⋅(-7)3+c⋅(-7)+5=f(-7)+10=17. Ebből f(7)=-17.
 
4. Szivárvány akkor alakul ki, ha az egymástól csak kicsit eltérő irányban érkező fénysugarak a fény többszöri törése és visszaverődése után gyakorlatilag azonos irányban (csak másodrendűen kicsit különböző irányokban) hagyják el a cseppet. Megmutatható, hogy a vízben lévő légbuborékoknál (amelynél a fénytörés úgy írható le, mintha a törésmutató 1/n lenne) ez nem fordulhat elő.
 
5. Legyenek a befogók a és b, az átfogó pedig c. Tegyük fel először, hogy a=2k+1 és b=2l+1 (ahol k és l természetes számok). A Pitagorasz-tétel szerint ekkor c2=(a+b)2=(2k+1)2+(2l+1)2=4(k2+l2+k+l)+2, tehát c2 páros, de nem osztható 4-gyel, ami lehetetlen. Ebből következik, hogy vagy mind a három oldal páros, vagy az egyik befogó páros, a másik befogó és az átfogó pedig páratlan. Mindkét esetben t=ab2, s=a+b+c2 és r=a+b-c2 is egész szám.
 

6. A nyomás a vödör fenekén nagyobb, mint a víz felszínénél. A vödör közepén lévő víz körmozgásához szükséges centripetális erőt éppen ez a nyomáskülönbség hozza létre. A Bernoulli-törvény ,,cirkulációval'' (önmagukba záródó áramvonalakkal) rendelkező áramlásoknál (a víz mozgása ebben az esetben ilyen) csak egy-egy áramvonal mentén érvényes.
 
7. A legkisebb szám biztosan nem nagyobb a szomszédainak átlagánál. Mutatunk egy példát arra, amikor a maradék hét csúcsba írt szám mindegyike nagyobb, mint a szomszédainak átlaga.

 
 

 
8. Általános érvényű termodinamikai megfontolásokkal belátható, hogy a cp-cV fajhőkülönbség a hőtágulási együttható négyzetével arányos, tehát annak előjelétől függetlenül mindig pozitív.
 
9. Húsz egyenes metszéspontjainak száma legfeljebb (202)=190. Mivel 5 egyenes párhuzamos, ezért a metszéspontokból (52)=10 nem jön létre. Az öt egy ponton átmenő egyenes esetében pedig (52)-1=9 metszéspontot ,,veszítünk''. Ez legfeljebb 190-10-9=171 metszéspontot adhat.
 
10. Igen, létezhet ilyen mező! Egy körvezető és annak forgási szimmetriatengelyében haladó egyenes áramvezető együttes mágneses terében a körvezetőre meggörbített dugóhúzóként feltekeredő erővonalak ‐ amennyiben a két vezetőben folyó áramerősségek aránya irracionális szám ‐ sosem záródnak. (Ez azonban csak egy matematikai érdekesség, hiszen két fizikai mennyiség arányának racionális vagy irracionális voltát véges pontosságú méréssel nem lehet eldönteni.)
 
11. Az Audik száma vagy 2-vel csökken, vagy változatlan marad, tehát a 10-ből sosem lehet 1.
 
12. Normál állapotú levegőben a gázmolekulák átlagos távolsága mintegy 10-9 m, ez csak 1 nagyságrenddel nagyobb, mint a molekulák kb. 10-10 m-es mérete. Ugyanakkor a csillagok fényév nagyságrendű távolsága sok-sok nagyságrenddel nagyobb, mint a csillagok tipikus mérete (10-10 fényév). A csillagok alkotta ,,gáz'' tehát a galaxisokban sokkal ritkább, mint az atomokból (molekulákból) álló valódi gázok.
 
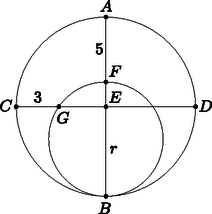
13. Jelölje a nagy kör sugarát r. Ekkor EF=r-5 és EG=r-3. A szelőszakaszok tételéből EG2=EF⋅EB, vagyis (r-3)2=(r-5)⋅r. Ezt megoldva r=9, és így az átmérők 18 cm és 13 cm.

 
 

13+1. Ha a gyöngysor függőleges egyenes mentén esne le, akkor (az energiamegmaradás törvénye szerint) minden gyöngyszem sebessége a kérdéses pillanatban éppen (3/4)Lg lenne. A leeső gyöngysor alakja azonban nem egyenes, hanem egy ostor végéhez hasonlóan hullámos lesz az asztallap szélének közelében. Emiatt a legalsó gyöngyszem nem kerülhet olyan mélyre, mintha a gyöngysor egyenes lenne, és így az egész gyöngysor sebességének (mozgási energiájának) is kisebbnek kell lennie, mint amekkora az egyenesen lecsúszó gyöngysoré lenne.
A gyöngysor ,,hullámosodásának'' szükségszerű bekövetkezését a vízszintes irányú lendület megmaradásával indokolhatjuk. Egy élesen bekanyarodó, de még csak félig lecsúszott gyöngysornak biztosan lenne vízszintes irányú lendülete, a teljesen lecsúszottnak pedig nem, jóllehet a gyöngyök rendszerére nem hat vízszintes irányú, visszafelé húzó erő. Az asztal pereme által kifejtett erőnek van ugyan vízszintes összetevője, de ez ,,előre'' mutat, és az éles kanyarhoz egy bizonyos sebesség felett már visszahúzó vízszintes erőkomponensre lenne szükség; ilyen azonban nincs. Tehát kezdetben bekanyarodik a lánc, csak később jelentkezik az ostorosodás.