Cím: A 47. Nemzetközi Fizikai Diákolimpia elméleti feladatai
Füzet: 2016/október, 425 - 434. oldal  PDF  |  MathML 
Témakör(ök): Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1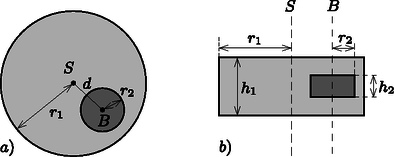
1. feladat. Két mechanikai probléma (összesen 10 pont).
A rész. Elrejtett korong (3,5 pont)
Tekintsünk egy tömör, fából készült, r1 sugarú és h1 vastagságú hengert. A fahenger belsejében valahol a fa anyaga helyett egy r2 sugarú és h2 vastagságú fémkorong található. A fémkorong úgy helyezkedik el, hogy B szimmetriatengelye párhuzamos a fahenger S tengelyével, és ugyanakkora távolságra van a fahenger alsó és felső alaplapjától. Jelöljük S és B távolságát d-vel! A fa sűrűsége ϱ1, a fém sűrűsége pedig ϱ2>ϱ1. A fahenger és a fémkorong össztömege M.
Ebben a részben a fahengert a földre helyezzük, így jobbra és balra szabadon tud gördülni. Az elrendezés oldal- és felülnézetben az 1. ábrán látható.


 

1. ábra. a) oldalnézet; b) felülnézet
 

Ebben a feladatban a fémkorong méretét és helyét kell meghatározni.
A következőkben, ha a választ az ismert mennyiségekkel kell kifejeznünk, mindig az alábbiakat tekinthetjük ismertnek:
r1,h1,ϱ1,ϱ2   és  M.(1)

A cél r2, h2 és d meghatározása indirekt méréseken keresztül.
Jelöljük b-vel a teljes rendszer C tömegközéppontjának és a fahenger S szimmetriatengelyének távolságát! Ennek a távolságnak a meghatározásához a következő kísérletet tervezzük: a fahengert vízszintes alapra helyezzük úgy, hogy stabil egyensúlyban legyen. Az alapot lassan megdöntjük α szöggel (2. ábra). A tapadási súrlódás miatt a fahenger csúszás nélkül gördülhet. A henger egy kicsit lejjebb gördül a lejtőn, de végül valamekkora φ szögelfordulás után a stabil egyensúlyi helyzetben megáll. A φ szöget megmérhetjük.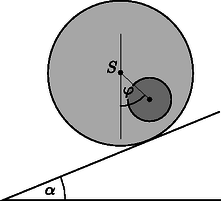


 

2. ábra. A henger a lejtőn
 

A.1. Fejezzük ki b-t az (1)-ben felsorolt mennyiségek, a φ szög és az α hajlásszög függvényében! (0,8 pont)
Mostantól kezdve b értékét ismertnek tekinthetjük.
A továbbiakban szeretnénk megmérni a rendszer ΘS tehetetlenségi nyomatékát az S szimmetriatengelyre vonatkoztatva. Ehhez egy mereven rögzített rúddal felfüggesztjük a fahengert a szimmetriatengelyénél. Ezután az egyensúlyi helyzetéből kicsiny φ szöggel kitérítjük, majd elengedjük (3. ábra). Azt találjuk, hogy φ periodikusan változik T periódusidővel.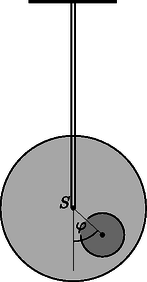


 

3. ábra. A felfüggesztett rendszer
 

A.2. Határozzuk meg φ mozgásegyenletét! Fejezzük ki a hengernek az S szimmetriatengelyére vonatkoztatott ΘS tehetetlenségi nyomatékát T, b és az (1)-ben felsorolt, ismert mennyiségek segítségével! Feltételezhetjük, hogy az egyensúlyi helyzettől való kitérés kicsi, így φ a mozgás során mindvégig igen kicsiny marad. (0,5 pont)
Az A.1. és A.2. részfeladatok mérései alapján szeretnénk meghatározni a fahengerben található fémkorong geometriáját és elhelyezkedését.
A.3. Fejezzük ki a d távolságot b és az (1)-ben szereplő mennyiségek segítségével. A formulában az r2 és h2 mennyiségeket is használhatjuk, hiszen ezeket az A.5. pontban meg fogjuk határozni. (0,4 pont)
A.4. Fejezzük ki az ΘS tehetetlenségi nyomatékot b és az (1)-ben szereplő, ismert mennyiségek segítségével. A formulában az r2 és h2 mennyiségeket is használhatjuk, hiszen ezeket az A.5. pontban meg fogjuk határozni. (0,7 pont)
A.5. A fenti eredményeket felhasználva fejezzük ki h2 és r2 értékét b, T és (1)-ben szereplő, ismert mennyiségek segítségével. A h2 mennyiséget kifejezhetjük r2-vel is. (1,1 pont)
 
B rész. Forgó űrállomás (6,5 pont)
Alice egy űrállomáson lakó űrhajós. Az űrállomás egy óriási, R sugarú kerék, amely a tengelye körül forog, így biztosítva a mesterséges gravitációt az asztronauták számára. Az űrhajósok a kerék peremének belső oldalán élnek. Az űrállomás gravitációs vonzása és a padló görbültsége elhanyagolható.
 
B.1. Mekkora ω0 szögsebességgel forog az űrállomás, ha az űrhajósok ugyanakkora gF gravitációs gyorsulást éreznek, mint a Föld felszínén? (0,5 pont)
Alice és űrhajós barátja, Bob vitatkoznak. Bob nem hiszi el, hogy valóban egy űrállomáson élnek, szerinte ténylegesen a Földön tartózkodnak. Alice fizikai módszerrel szeretné bebizonyítani Bobnak, hogy egy forgó űrállomáson élnek. Ezért egy m tömegű testet rögzít egy k rugóállandójú rugó végére, majd rezgésbe hozza. A test csak függőleges irányban rezeghet, vízszintesen nem tud mozogni.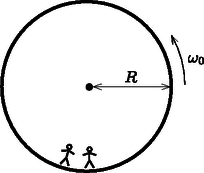
 
B.2. Feltételezve, hogy a Földön a gravitációs gyorsulás állandó gF, mekkorának mérné a rezgés ωF körfrekvenciáját egy Földön lévő személy? (0,2 pont)


 

4. ábra. Az űrállomás
 

 
B.3. Mekkora ω körfrekvenciát mér Alice az űrállomáson? (0,6 pont)
Alice meg van győződve arról, hogy a kísérlete bizonyíték arra, hogy egy forgó űrállomáson élnek. Bob szkeptikus marad. Szerinte ha a gravitációs tér Föld felszíne feletti változását is figyelembe vesszük, annak hasonló hatása van. A továbbiakban azt vizsgáljuk, igaza van-e Bobnak.
 
B.4. Fejezzük ki a gF(h) gravitációs gyorsulást kicsiny h magasságban a Föld felszíne fölött, és számítsuk ki a rezgő test ωF˜ körfrekvenciáját (elég a lineáris közelítés). A Föld sugarát jelölje RF. A Föld forgását figyelmen kívül hagyhatjuk. (0,8 pont)
Alice azt találja, hogy ezen az űrállomáson a rezgő test valóban a Bob által jósolt frekvenciával rezeg.
 
B.5. Mekkora az űrállomás R sugara, ha a rezgés ω körfrekvenciája megegyezik a Földön mérhető ωF˜ körfrekvenciával? A választ RF segítségével adjuk meg. (0,3 pont)
Bob makacsságán feldühödve Alice egy új kísérlettel áll elő saját igazának bizonyítására. Ezért felmászik az űrállomás padlója fölé H magasságba egy toronyra, és elejt egy testet. Ez a kísérlet értelmezhető a forgó vonatkoztatási rendszerben éppúgy, mint az inerciarendszerben.
Egy egyenletesen forgó vonatkoztatási rendszerben az űrhajós egy fiktív FC erőt tapasztal, amit Coriolis-erőnek nevezünk. Az állandó ω0 szögsebességgel forgó rendszerben v sebességgel mozgó, m tömegű testre ható FC Coriolis-erőt a következő összefüggés adja meg:
FC=2mv×ω0.
Használható a skaláris mennyiségekre vonatkozó
FC=2mvω0sinφ
alak, ahol φ a sebességvektor és a forgástengely közötti szög. Az erő merőleges mind a v sebességvektorra, mind pedig a forgástengelyre. Az erő előjele a jobbkéz-szabály alapján határozható meg, de ez az előjel a következőkben szabadon választható.
B.6. Számítsuk ki a test vx vízszintes sebességét és a vízszintes dx elmozdulását (a torony aljához képest, a toronyra merőleges irányban) a padlóra érés pillanatában. Feltehetjük, hogy a torony H magassága kicsiny, így az űrhajósok által mért gyorsulás az esés alatt állandó. Feltételezhető továbbá, hogy dx≪H. (1,1 pont)
Hogy jobb eredményt kapjon, Alice úgy dönt, hogy a kísérletet egy, a korábbinál sokkal magasabb toronyról is elvégzi. Meglepetésére a test a torony aljánál éri el a padlót, azaz dx=0.
B.7. Határozzuk meg a torony magasságának alsó korlátját, amelyre dx=0 lehetséges. (1,3 pont)
Alice szeretne még egy utolsó kísérletet tenni Bob meggyőzésére. A rugós rendszert szeretné használni a Coriolis-erő hatásának szemléltetésére. Ezért megváltoztatja az eredeti elrendezést: a rugót egy olyan gyűrűhöz rögzíti, amely szabadon és súrlódásmentesen csúszhat az x irányban egy vízszintes rúdon. A rugó maga az y irányban rezeg. A rúd párhuzamos a talajjal és merőleges az űrállomás forgástengelyére. Az x-y sík tehát merőleges a forgástengelyre, az y irány pedig egyenesen az űrállomás forgástengelye felé mutat.
B.8. Alice a testet az x=0, y=0 egyensúlyi állapotából d távolsággal kitéríti lefelé, majd elengedi (lásd az 5. ábrát).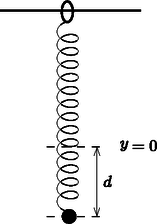


 

5. ábra. Az elrendezés
 

(i) Fejezzük ki az x(t) és y(t) mennyiségeket. Feltehetjük, hogy ω0d kicsi, és elhanyagolhatjuk az y irányú Coriolis-erőt.
(ii) Vázoljuk fel az (x(t),y(t)) pályát, és jelöljük minden fontos tulajdonságát, mint pl. az amplitúdóját. (Összesen 1,7 pont)
Alice és Bob folytatja vitáját ...
2. feladat. Nemlineáris dinamika elektromos áramkörökben (10 pont).
Bevezetés. Bistabil, nemlineáris félvezető áramköri elemeket (pl. tirisztorokat) széles körben alkalmaznak az elektronikában kapcsolóként és elektromágneses rezgések előállításához. A tirisztorok alkalmazásának elsődleges területe a váltóáram szabályozása a teljesítményelektronikában, például amikor megawattos nagyságrendben kell váltóáramot egyenirányítani. A bistabil elemek önszabályozó jelenségek modelljeként is szolgálhatnak a fizikában (ezzel foglalkozik a feladat B része), a biológiában (lásd a C részt) és a modern tudomány más, nemlineáris jelenségekkel foglalkozó területein.
Célkitűzések. Instabilitások és nemtriviális dinamika tanulmányozása nemlineáris I‐ V karakterisztikájú elemeket tartalmazó áramkörökben. Megmutatni ezen áramkörök felhasználási lehetőségeit a mérnöki gyakorlatban és a biológiai rendszerek modelezésben.
A. rész. Stacionárius állapotok és instabilitások (3 pont)
Az 6. ábra egy nemlineáris X áramköri elem úgynevezett S-alakú I-U karakterisztikáját mutatja. Az Ut=4,00 V (tartófeszültség) és a Uk=10,0 V (küszöbfeszültség) közötti feszültségtartományban az I‐ U karakterisztika többértékű. Az egyszerűség kedvéért a 6. ábrán látható grafikon szakaszonként lineáris (minden ág egy egyenes szakasz), továbbá a felső ág meghosszabbítása átmegy az origón. Ez a közelítés jól leír egy valódi tirisztort.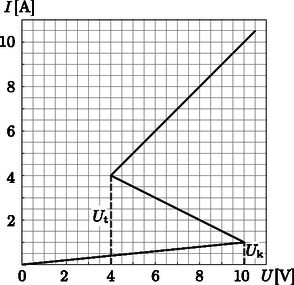


 

6. ábra. Az X nemlineáris elem I‐ U karakterisztikája
 

A.1. A grafikon alapján határozzuk meg az X áramköri elem Rbe és Rki ellenállását az I‐ U karakterisztika felső, illetve alsó ágában! A középső ágat a következő egyenlet írja le:
I=I0-URk.

Határozzuk meg az I0 és Rk paraméterek értékét! (0,4 pont)
Az X áramköri elem sorba van kötve egy R ellenállással, egy L induktivitással és egy E ideális feszültségforrással (lásd a 7. ábrát). Az áramkört stacionárius állapotban lévőnek nevezzük, ha az áramerősség 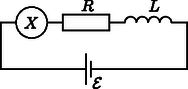I(t)=állandó.


 

7. ábra. Áramkör az X elemmel, az R ellenállással, az L induktivitással és az E feszültségforrással
 

A.2. Hány stacionárius állapota lehet a 7. ábrán látható áramkörnek, ha E egy rögzített érték és R=3,00Ω? Hogyan módosul a válasz, ha R=1,00Ω? (1 pont)
A.3. Legyen a 7. ábrán látható áramkörben R=3,00Ω, L=1,00μH és E=15,0V. Határozzuk meg az X áramköri elem Ist áramának és Ust feszültségének értékét a stacionárius állapotban! (0,6 pont)
A 7. ábrán látható áramkör stacionáris állapotban van, ahol I(t)=Ist. Ezt a stacionárius állapotot stabilnak nevezzük, ha az áramerősség egy kis változtatás (növelés vagy csökkentés) után visszatér a stacionárius állapotba. Ha viszont a rendszer egyre jobban eltávolodik a stacionárius állapottól, akkor ezt az állapotot instabilnak nevezzük.
A.4. Használjuk az A.3. kérdésben szereplő numerikus értékeket, és tanulmányozzuk az I(t)=Ist áramú stacionárius állapot stabilitását! Stabil vagy instabil ez az állapot? (1 pont)
 
B. rész. Bistabil, nemlineáris áramköri elemek a fizikában: rádióadó (5 pont)
Most egy új áramköri elrendezést vizsgálunk (lásd a 8. ábrát). Ez alkalommal az X nemlineáris áramköri elem párhuzamosan van kötve egy C=1,00μF kapacitású kondenzátorral. Ezt aztán sorbakötjük egy R=3,00Ω ellenállású ellenállással és egy E=15,0V állandó feszültségű, ideális feszültségforrással. Kiderül, hogy az áramkör rezgéseket végez, azaz az X nemlineáris áramköri elem az I‐ U karakterisztika egyik ágáról a másikra ugrik egy ciklus során.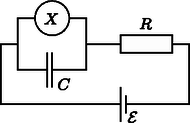


 

8. ábra. Áramkör az X elemmel, az R ellenállással, az L induktivitással és az E feszültségforrással
 

 
B.1. Rajzoljuk le a rezgési ciklust az I‐ U grafikonon, és adjuk meg az irányát is (óramutató járásával megegyező vagy azzal ellentétes). Indokoljuk a választ egyenletekkel és vázlatokkal! (1,8 pont)
 
B.2. Vezessünk le kifejezéseket azon t1 és t2 időtartamokra, amelyeket a rendszer az I‐ V grafikon egyes ágain tölt a rezgési ciklus során! Számítsuk ki ezek numerikus értékét is! Határozzuk meg a rezgés T periódusidejét is, feltételezve, hogy az az idő, ami az I‐ U grafikon egyik ágáról a másik ágára való átugráshoz szükséges, elhanyagolható! (1,9 pont)
 
B.3. Becsüljük meg a nemlineáris elemen egy ciklus alatt disszipálódó átlagos P teljesítményt! Elég a nagyságrendet meghatározni. (0,7 pont)
A 8. ábrán látható áramkört egy rádióadóhoz használjuk. Az X áramköri elemet egy s hosszúságú lineáris antenna (egy hosszú, egyenes vezeték) egyik végéhez csatlakoztatjuk, a vezeték másik vége szabad. Az antennában egy elektromágneses állóhullám alakul ki. Az elektromágneses hullám sebessége az antenna mentén ugyanakkora, mint vákuumban. Az adó a rendszer alapharmonikusát használja, melynek periódusideje a B.2. részben meghatározott T.
 
B.4. Mi az s hosszúság optimális értéke, feltéve, hogy nem haladhatja meg az 1km-t? (0,6 pont)
 
C. rész. Bistabil, nemlineáris áramköri elemek a biológiában:
neurisztor (2 pont)
A feladat ezen részében a bistabil, nemlineáris áramköri elemet egy biológiai folyamat modelljeként vizsgáljuk. Egy neuron az emberi agyban a következő tulajdonsággal rendelkezik: ha egy külső jel ingerli, akkor egyetlen rezgést végez, majd visszatér az eredeti állapotába. Ezt a tulajdonságot ingerelhetőségnek nevezzük. Ennek a tulajdonságnak köszönhetően impulzusok haladhatnak végig az idegrendszert alkotó, csatolt neuronok hálózatán. Azt a félvezető csipet, amelyet az ingerelhetőség és a jelterjedés utánzására készítenek, neurisztornak nevezik (a neuron és a tranzisztor szavakból).
Megkísérlünk egy egyszerű neurisztort egy olyan áramkörrel modellezni, mely tartalmazza az eddig vizsgált X nemlineáris elemet. Ezért a 8. ábrán látható áramkörben az E feszültséget lecsökkentjük E'=12,0V-ra. A rezgések megszűnnek, és a rendszer eléri stacionárius állapotát. Aztán a feszültséget hirtelen újra E=15,0V-ra növeljük, majd τ időtartam után (ahol τ<T) ismét E' értékre állítjuk (lásd a 9. ábrát). Kiderül, hogy van egy bizonyos kritikus τk érték, és a rendszer minőségileg más viselkedést mutat, ha τ<τk, illetve ha 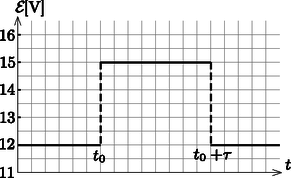τ>τk.


 

9. ábra. A feszültségforrás feszültsége az idő függvényében
 

C.1. Vázoljuk fel az X áramköri elemen folyó IX(t) áramerősséget az idő függvényében ha τ<τk, illetve ha τ>τk! (1,2 pont)
C.2. Fejezzük ki paraméteresen és határozzuk meg numerikusan is, hogy mekkora az a τk kritikus idő, ahol a viselkedés megváltozik. (0,6 pont)
C.3. Neurisztor-e az áramkör τ=1,00⋅10-6s érték esetén? (0,2 pont)
 
3. feladat. A Nagy Hadronütköztető (10 pont).
Ez a feladat a CERN-ben működő részecskegyorsító, a Nagy Hadronütköztető (Large Hadron Collider, LHC) fizikájával foglalkozik. A CERN a világ legnagyobb részecskefizikai laboratóriuma. Célja, hogy betekintést nyújtson a természet alapvető törvényeibe.
Az LHC-ben két részecskenyalábot gyorsítanak fel nagy energiára úgy, hogy azokat erős mágneses térrel gyorsítógyűrűben vezetik, és utána egymással ütköztetik őket. A protonok nem egyenletesen, hanem úgynevezett csomagokba rendeződve oszlanak el a gyorsító kerülete mentén. Az ütközés során keletkezett részecskéket hatalmas méretű detektorokkal figyelik meg. Az LHC néhány paramétere az 1. táblázatban található.
 
LHC gyűrű   Gyűrű kerülete    26 659 mRészecskecsomagok száma egy protonnyalábban    2808  Protonok száma egy részecskecsomagban  1,15⋅1011Protonnyalábok   Protonok energiája    7,00 TeV  Tömegközépponti energia    14,0 TeV  

 
1. táblázat. Az LHC releváns paramétereinek jellemző numerikus értékei
 

A részecskefizikusok az SI mértékegysékegnél alkalmasabb egységeket használnak az energia, az impulzus és a tömeg kifejezésére. Az energiát elektronvoltban [eV] mérik. Definíció szerint 1 eV energiát nyer az az e elemi töltéssel rendelkező részecske, amelyik 1 volt potenciálkülönbségen haladt át (1eV=1,602⋅10-19kg m2s-2). Az impulzust eV/c, a tömeget eV/c2 egységekben adják meg, ahol c a vákuumbeli fénysebesség. Mivel 1 eV nagyon kicsi energiamennyiség, a részecskefizikusok gyakran a MeV (1MeV=106eV), a GeV (1GeV=109eV) vagy a TeV (1TeV=1012eV) egységeket használják.
A feladat első része a protonok vagy az elektronok gyorsításával, a második rész pedig az ütközéskor keletkezett részecskék azonosításával foglalkozik.
A rész. Az LHC gyorsító (6 pont)
Gyorsítás. Tegyük fel, hogy a protonokat U feszültséggel gyorsítjuk fel a fénysebességhez nagyon közeli sebességre. Hanyagoljuk el a sugárzásból és más részecskékkel való ütközésből eredő energiaveszteségeket.
A.1. Adjuk meg a protonok v végsebességének pontos kifejezését az U gyorsítófeszültség és fizikai állandók függvényében! (0,7 pont)
Egy jövőbeli, tervezett kísérletben az LHC-ből érkező protonokat 60,0 GeV energiájú elektronokkal ütköztetik.
A.2. Egy nagyenergiájú és kicsi tömegű részecskére a v végsebesség és a c fénysebesség közötti Δ=(c-v)/c relatív eltérés nagyon kicsi. Adjunk ,,első közelítést'' Δ-ra, és számítsuk ki Δ értékét 60,0GeV energiájú elektronokra az U gyorsítófeszültség és fizikai állandók segítségével! (0,8 pont)
Most visszatérünk az LHC-beli protonokra. Tegyük fel, hogy a nyalábot vezető cső kör alakú.
A.3. Vezessük le a protonnyaláb kör alakú pályán tartásához szükséges homogén mágneses indukció B nagyságát megadó összefüggést! A kifejezés csak a protonok E energiáját, az L kerületet, fizikai állandókat és számokat tartalmazhat. Megfelelő közelítések használata megengedett, ha azok hatása az utolsó értékes jegy pontosságánál kisebb.
Számítsuk ki a B mágneses indukciót, elhanyagolva a protonok közötti kölcsönhatásokat, ha a proton energiája E=7,00TeV. (1 pont)
Kisugárzott teljesítmény. Egy gyorsuló, töltött részecske elektromágneses hullám formájában energiát sugároz. Az állandó szögsebességgel keringő, töltött részecske által kisugárzott Ps teljesítmény csak az a gyorsulásától, a q töltésétől, a c fénysebességtől és a vákuum ε0 permittivitásától függ.
A.4. Dimenzióanalízissel adjuk meg a Ps kisugárzott teljesítmény kifejezését! (1 pont)
A kisugárzott teljesítmény pontos képletében még egy (1/6π)-s szorzótényező is szerepel, továbbá a relativisztikus levezetés egy γ4-es szorzótényezőt is tartalmaz, ahol γ=(1-v2/c2)-1/2.
A.5. Számítsuk ki az LHC Pt teljes kisugárzott teljesítményét, ha a proton energiája E=7,00TeV (1. táblázat). Alkalmas közelítések használata megengedett. (1 pont)
Lineáris gyorsító. A CERN-ben nyugvó protonokat gyorsítanak fel 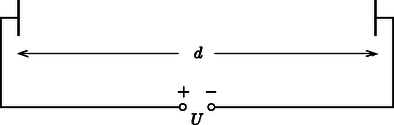d=30,0 m hosszúságú lineáris gyorsítóval U=500 MV potenciálkülönbségen keresztül. Tegyük fel, hogy az elektromos mező homogén. A lineáris gyorsító két lemezből áll, ahogyan azt (vázlatosan) a 10. ábra mutatja.


 

10. ábra. A gyorsítóegység vázlata
 

A.6. Határozzuk meg azt a T időt, ami alatt a protonok áthaladnak ezen az elektromos mezőn! (1,5 pont)
B rész. Részecskeazonosítás (4 pont)
Repülési idő. A kölcsönhatási folyamatok értelmezéséhez fontos az ütközésekben keletkező, nagyenergájú részecskék azonosítása. Létezik egy egyszerű módszer, amivel azt az időt (t) mérik, ami ahhoz szükséges, hogy egy ismert impulzusú részecske ℓ utat tegyen meg egy ún. repülési idő (RI) detektorban. A detektorban azonosított néhány, tipikus részecskét és a tömegüket a 2. táblázat tartalmazza.
 
Részecske   Tömeg   [MeV /  c2]Deuteron    1876  Proton    938Töltött kaon    494Töltött pion    140  Elektron    0,511  

 
2. táblázat. Részecskék és tömegeik
 

B.1. Fejezzük ki a részecske 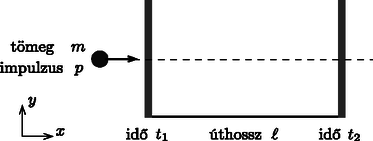m tömegét a p impulzus, az ℓ repülési úthossz és a t repülési idő függvényében. Feltételezhetjük, hogy a részecske az e elemi töltéssel rendelkezik, és az RI detektorban a c fénysebességhez nagyon közeli sebességgel egyenes pályán, a két érzékelési síkra merőlegesen halad (11. ábra)! (0,8 pont)


 

11. ábra. A repülési idő (RI) detektor sematikus ábrája
 

B.2. Számítsuk ki azon RI detektor legkisebb ℓ hosszát, amelyben a töltött kaon a töltött piontól biztosan megkülönböztethető, ha mindkét részecske impulzusát 1,00GeV/c-nek mérik! A jó elkülönítéshez az kell, hogy a repülési idők különbsége háromszor akkora legyen, mint a detektor időfelbontása. Egy RI detektor tipikus felbontása 150ps (1ps=10-12s). (0,7 pont)
A következőkben egy tipikus LHC detektorban létrejövő részecskéket olyan kétlépcsős detektorban azonosítjuk, amely egy nyomkövető detektorból és egy RI detektorból áll. A 12. ábra mutatja az elrendezést a protonnyalábok kereszt- és hosszanti irányában. Mindkét detektor egy-egy cső, amelyek körülveszik a kölcsönhatási területet, bennük a csövek közepén haladó nyalábbal. A nyomkövető detektor méri a protonnyalábbal párhuzamos irányú mágneses téren áthaladó töltött részecske pályáját. A pálya 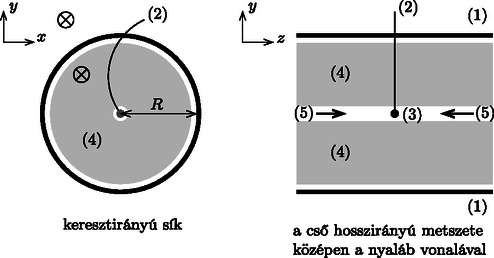r sugarával meghatározható a részecske keresztirányú pT impulzusa. Mivel az ütközés ideje ismert, az RI detektorhoz csak egy cső szükséges ahhoz, hogy mérjék a repülési időt az ütközési pont és az RI cső között. Ez az RI cső szorosan a nyomkövető kamra külsején helyezkedik el. Ebben a feladatban feltehetjük, hogy az ütközésben keletkezett összes részecske a protonnyalábokra merőlegesen halad. Ez azt jelenti, hogy a keletkező részecskék nem rendelkeznek a protonnyalábok irányába mutató impulzussal.


 

12. ábra. A részecskeazonosítás kísérleti elrendezése a nyomkövető kamrával és az RI detektorral. Mindkét detektor egy-egy cső, amelyek a középen levő ütközési pontot veszik körül. Bal oldal: keresztirányú nézet a nyaláb vonalára merőlegesen. Jobb oldal: hosszanti nézet a nyaláb vonalával párhuzamosan. (1) ‐ RI cső; (2) ‐ pálya; (3) ‐ ütközési pont; (4) ‐ nyomkövetési cső; (5) ‐ protonnyalábok; ⊗ ‐ mágneses tér
 

B.3. Fejezzük ki a részecske tömegét a B mágneses indukcióval, az RI cső R sugarával és fizikai állandókkal, valamint a mért mennyiségekkel: az r pályasugárral és a t repülési idővel! (1,7 pont)
Négy részecskét detektáltunk, és szeretnénk ezeket azonosítani. A nyomkövető detektorban a mágneses indukció B=0,500T. Az RI cső R sugara 3,70m. A mérési eredmények a következők (1ns=10-9s):
 
Részecske   r   pályasugár  [m]  t  repülési idő  [ns]A    5,10    20B    2,94    14C    6,06    18D    2,31    25
 

B.4. Azonosítsuk a négy részecskét a tömegük kiszámításával! (0,8 pont)
1A hivatalos megoldást és a mérési feladatokat a KöMaL novemberi számában ismertetjük.
A feladatok kidolgozására 5 óra állt rendelkezésre. A három elméleti feladatra összesen 30 pontot lehetett kapni. A részfeladatok után közölt pontszámok az egyes kérdések nehézségi fokára utalnak.
A versenyzők a feladatlapok mellé egy táblázatot is kaptak, amely a természeti állandók értékeit és néhány atomi részecske adatait tartalmazta. Ezeket az adatokat Olvasóink megtalálhatják pl. a ,,Négyjegyűben'', ezért a táblázatot nem közöljük.