Kezdőlap


Cím:	Feltevés és realitás
Szerző(k):	Holics László
Füzet:	1992/január, 42 - 46. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egy golyót az asztal szélén, az ábrán látható helyzetben elengedünk. A golyó melyik helyzetében válik el az asztal szélétől, ha a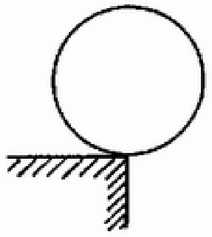
a) súrlódás elhanyagolható,
b) nagyon nagy?

\begin{matrix} ⋆ \end{matrix}

Vizsgáljuk meg a megoldás feltevéseinek realitását, azaz az a) esetbeli

μ = 0

és a b) esetbeli ,,igen nagy'' értéket! A műszaki megoldás realitásához tartozik, hogy megvizsgáljuk a táblázatokban található legkisebb és legnagyobb súrlódási együtthatóval való számolás esetén a megoldásmenet korrektségét, és összehasonlítjuk a realitásnak engedményeket tevő egyszerűsítő feltevésekkel kapható megoldásmenet korrektségével. Erre igen érdekes példa ez a feladat.
Az Omacht‐Sárközi: Műszaki Táblázatok c. kötetben található legkisebb súrlódási együttható

μ = 0, 028

(acél jégen), a legnagyobb pedig

μ = 0, 76

(kő betonon). Úgy tűnik, hogy az első adat valóban közel áll a feltételezett

0

értékhez, és elvileg a másodiknál is vehetünk sokkal nagyobbat (

μ > 1

-nek sincs elvi akadálya), de kérdés, meddig térhetünk el a reális értékektől, ha nem akarjuk ,,fogaskerékre'' és ,,fogaslécre'' átfogalmazni az ilyen típusú feladatokat? Erre a kérdésre csak úgy válaszolhatunk megnyugtatóan, hogy felveszünk egy tetszőleges

μ

értéket, és megvizsgáljuk, hogy ennek zérus felé való csökkentése ill. ,,végtelen'' felé való növelése befolyásolja-e a megoldás menetének elvi tisztaságát.
A feladat közölt megoldásában a

μ = 0

feltevést elég jól tűrik a megoldásban alkalmazott fizikai törvények, azonban látni fogjuk, hogy a ,,

μ

legyen igen nagy érték'' csak akkor elegendően nagy, ha pont ,,végtelen''! Ez pedig már túl van a realitások nagyvonalúan kezelt határain is, mert a ,,végtelen'' és az ,,igen nagy'' igen távol van egymástól! A közölt megoldás feltétele, vagyis a golyó elválásig való csúszásmentessége csak

μ = \infty

esetben valósul meg, ugyanis véges súrlódási együttható esetén a golyó az

53, 96^{\circ}

elérése előtt feltétlenül megcsúszik, mert a 0-hoz tartó kényszererő képtelen biztosítani a csúszásmentességhez szükséges szöggyorsulást okozó tapadási súrlódási erőt. Így a megoldásban alkalmazott mechanikai energia megmaradására felírt egyenlet a golyó asztaltól való elválása előtt érvényét veszti, mert a csúszási súrlódás közben az energia egy része disszipálódik.
Ezen bevezető után gondolhatnánk, hogy a közölt megoldás teljesen hibás. Látni fogjuk azonban, hogy ez nincs így, de néhány gondolatot érdemes kifejteni a megoldás kapcsán. Egyszerre két dolgot vizsgálunk meg: egyrészt honnan kezdve elvi hibás a megoldás, ha nem utalunk az alkalmazott elhanyagolásra, másrészt hogy miért jó a közölt megoldás, ha utalunk rá (és megbecsüljük az elhanyagolás mértékét).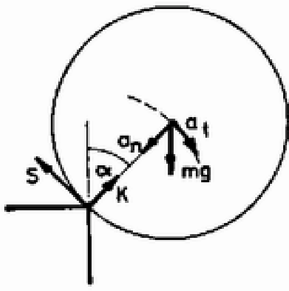

1. ábra

E célból határozzuk meg különböző értékű súrlódási együtthatók esetén a golyó megcsúszásához tartozó szögelfordulást! Egyenleteink a tiszta gördülésig érvényesek, a tapadási erőre vonatkozó egyenlőtlenség pedig éppen a megcsúszás pillanatáig:

\begin{matrix} m g sin α - S = m a_{t} \end{matrix}

(1)

(mozgásegyenlet a tömegközéppont tangenciális mozgására),

\begin{matrix} m g cos α - K = m a_{n} \end{matrix}

(2)

(mozgásegyenlet a tömegközéppont normálirányú mozgására),

\begin{matrix} S R = \frac{2}{5} m R^{2} β \end{matrix}

(3)

(forgatónyomaték-tétel),

\begin{matrix} S \leq μ K \end{matrix}

(4)

(a tapadási súrlódási erő értéke megcsúszás előtti pillanatig),

\begin{matrix} m g R (1 - cos α) = \frac{1}{2} m v^{2} + \frac{1}{2} \cdot \frac{2}{5} m R^{2} ω^{2} \end{matrix}

(5)

(mechanikai energia megmaradásának tétele),

\begin{matrix} a_{t} = R β \end{matrix}

(6)

(a csúszásmentes gördülés szükséges feltétele),

\begin{matrix} v = R ω \end{matrix}

(7)

(a csúszásmentes gördülés elégséges feltétele).
Az egyenletrendszer megoldása cos

α

-ra:

\begin{matrix} cos α = \frac{340 μ^{2} \pm \sqrt[]{340^{2} μ^{4} - 4 \cdot (100 μ^{2} - 4) (289 μ^{2} + 4)}}{2 (289 μ^{2} + 4)} . \end{matrix}

Készítsünk táblázatot arra vonatkozóan, hogy különböző súrlódási együtthatók esetén a golyó mekkora szögelfordulás után csúszik meg!

\begin{matrix} \begin{matrix} μ & 0,01 & 0,028 & 0,1 & 0,2 & 0,5 & 0,76 & 1 & 2 & 10 & \infty \\ α & 2, 03^{\circ} & 5, 56^{\circ} & 17, 97^{\circ} & 29, 07^{\circ} & 41, 8^{\circ} & 45, 66^{\circ} & 47, 54^{\circ} & 50, 7^{\circ} & 53, 29^{\circ} & 53, 96^{\circ} \end{matrix} \end{matrix}

Az utolsó értékpár egzakt megoldással úgy kapható meg, hogy az egyenletrendszert

μ

-re oldjuk meg, és meghatározzuk

α

értékét, amelyhez

μ = \infty

tartozik:

\begin{matrix} μ = \frac{2 sin α}{\sqrt[]{289 cos α^{2} - 340 cos α + 100}} . \end{matrix}

Ebből a kifejezésből látszik, hogy a súrlódási együttható akkor válik végtelenné, ha a nevező zérussá válik, vagyis a

\begin{matrix} 289 cos α^{2} - 340 cos α + 100 = 0 \end{matrix}

egyenlet megoldásaként kapott szög esetén. Innen

\begin{matrix} cos α = \frac{340 + \sqrt[]{340^{2} - 400 \cdot 289}}{2 \cdot 289} = \frac{340}{278} = \frac{10}{17}, \end{matrix}

ahonnan

α = 53, 96^{\circ}

, ami éppen a golyó elfordulási szögének a megoldásban közölt értéke, vagyis a golyó csak akkor nem csúszik meg az asztaltól való elválásig, ha a tapadási súrlódás együtthatója végtelen! Ilyet pedig a természet nem produkál, mesterségesen valamiféle ,,bütyökkel'' elő lehet ugyan állítani ennek megfelelő hatást, azonban ekkor már nem golyó a golyó.
Mint látható, a lecsúszó golyó a feladat a) kérdésében is kap egy kis forgási energiát, azonban ez valóban elhanyagolható, a b) kérdésre adott meggondolásban szereplő feltevés (

μ = \infty

) azonban túl nagy elrugaszkodás a realitásoktól, így a megoldásban elvi problémák lépnek fel.
Most megmutatjuk, hogy ha megbecsüljük a megoldásban figyelmen kívül hagyott energiadisszipációt, ami az ,,igen nagy'' de véges (pl.

0,76

értékű) súrlódási együttható miatt lép fel, és figyelembe vesszük a megoldáskor, igen kis numerikus eltérést kapunk a szélsőséges feltétellel kapotthoz képest.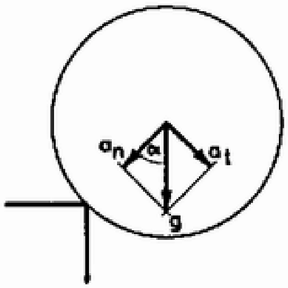

2. ábra

Amikor a golyó elhagyja az asztal sarkát, tömegközéppontjának gyorsulása

a

g

. Ennek pályaérintő- és normálirányú komponensei:

\begin{matrix} a_{n} = g cos α, illetve a_{t} = g sin α \end{matrix}

nagyságúak. Innen az asztal sarkától a golyó középpontjáig húzott pályasugár elfordulása szögének tangense az elválás pillanatában:

\begin{matrix} tg α = \frac{a_{t}}{a_{n}} = \frac{R g sin α}{v^{2}}, \end{matrix}

ahonnan

\begin{matrix} cos α = \frac{v^{2}}{R g} . \end{matrix}

(8)

A golyó elválásának szögét ismerjük, ha a golyó tömegközéppontjának pillanatnyi sebességét ismerjük az elváláskor. Ennek meghatározásába szól bele a megcsúszás. A mechanikai energia megmaradásának tétele nem alkalmazható, a munka-tétel viszont érvényes, és fel is írhatjuk, ha valamilyen módon meg tudjuk határozni a csúszási súrlódási erő munkáját.
Írjuk fel a munkatételt a megcsúszás pillanatától az asztal elhagyásáig! Jelölje a megcsúszás kezdetén meglevő szögelfordulást

α_{0}

, az elhagyás pillanatabeli (teljes) szögelfordulást

α

, a golyó e két helyzete közötti inerciarendszerbeli szögelfordulását

φ!

\begin{matrix} m g R (cos α_{0} - cos α) - \int_{0}^{α - α_{0} - φ} S R d α^{,} = \frac{1}{2} m (v^{2} - v_{0}^{2}) + \frac{1}{2} \cdot \frac{2}{5} m R^{2} (ω^{2} - ω_{0}^{2}), \end{matrix}

(9)

ahol

α^{'} = α - α_{0} - φ

, a relatív szögelfordulás, amivel a súrlódó felületek egymáson megtett útját mérjük a megcsúszástól az elválásig.
Ijesztőnek látszik a változó súrlódási erő munkájának integrállal való kiszámítása, valamint az, hogy semmiféle közvetlen kényszer-kapcsolatunk nincs a golyó tömegközéppontjának sebessége és forgásának (nem pályamozgásának!) szögsebessége között. Az előbbi gondot úgy kerülhetjük meg, hogy becslésünk során a kényszererő, ill. a vele arányos csúszási súrlódási erő szögelfordulástól való függését a várhatóan kicsiny szögtartományban lineáris függvénnyel közelítjük. A második problémát egyszerű meggondolással küszöbölhetjük ki. Ez a következő:
A csúszási súrlódási erő munkája esetünkben ‐ mint ahogy (9)-ből látható ‐ egy negatív és egy pozitív tag összege. A negatív tag abszolút értéke a nagyobb. Ez okozza az energiadisszipációt. A pozitív tag a golyó tömegközéppont körüli forgásának szögsebességét (energiáját) növeli, ez a tény azonban nem befolyásolja a tömegközéppont pályamozgásának sebességét, tehát az asztaltól való elválás körülményeit sem. A negatív tag játszik bele a golyó transzlációs sebességének alakításába.
A csúszva-gördüléskor végzett súrlódási munka számítását egy egyszerű példával világítjuk meg.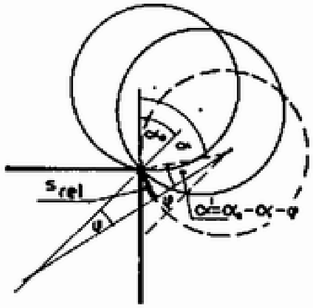

3. ábra

Gurítsunk el egy golyót érdes síkon úgy, hogy kezdetben csússzon! A súrlódási erőnek a golyón végzett munkája a súrlódási erő és a súrlódó felületek relatív elmozdulásának negatív előjellel vett szorzata:

\begin{matrix} W = - S s_{r e l} = - S (s - R φ), \end{matrix}

ahol

s

a tömegközéppont útja a nyugvó talajon,

φ

a golyó teljes szögelfordulása (az inerciarendszerhez képest). A munkatétel szerint:

\begin{matrix} W = \frac{1}{2} m (v^{2} - v_{0}^{2}) + \frac{1}{2} \cdot \frac{2}{5} m R^{2} (ω^{2} - ω_{0}^{2}) . \end{matrix}

Mivel

\begin{matrix} S R φ = \frac{1}{2} \cdot \frac{2}{5} m R^{2} (ω^{2} - ω_{0}^{2}), \end{matrix}

a munkatételre felírt egyenlet mindkét oldaláról elhagyható!
A fentiek szerint a

W = - S (s - R φ)

munkából a

- S \cdot s

a sebességet csökkenti, az

S R φ

a szögsebességet növeli. (Ez utóbbi nem számít az elválás szempontjából!)
Alkalmazzuk a mi esetünkre, figyelembe véve, hogy a lineáris közelítés miatt a súrlódási erő átlagát a számtani középpel számíthatjuk, ami a teljes megszűnésig a maximális értékének a fele! A maximális érték pedig a megcsúszás kezdetén mérhető érték: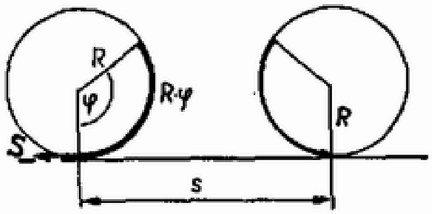

\begin{matrix}  \end{matrix}

\begin{matrix}  \end{matrix}

mgR(cosα0-cos α)-S02R(α-α0)+S02Rφ==12m(v2-v02)+12⋅25mR2(ω2-ω02).

(Figyelembe vettük, hogy a munkatételben korábban felírt

α^{'} = α - α_{0} - φ

, és hogy

\begin{matrix} \frac{S_{0}}{2} R φ = \frac{1}{2} \cdot \frac{2}{5} m R^{2} (ω^{2} - ω_{0}^{2}), \end{matrix}

amit mindkét oldalról elhagytunk.) Innen

v^{2}

-et kifejezve:

\begin{matrix} v^{2} = 2 g R (cos α_{0} - cos α) - \frac{S_{0}}{m} R (α - α_{0}) + v_{0}^{2} . \end{matrix}

Ezzel az elválás szögének koszinuszára kapott (8) összefüggés így írható:

\begin{matrix} cos α = 2 (cos α_{0} - cos α) - \frac{S_{0}}{m g} (α - α_{0}) + \frac{v_{0}^{2}}{R g} . \end{matrix}

4. ábra

Figyelembe véve, hogy a maximális súrlódási erő a tapadás utolsó pillanatában érvényes

\begin{matrix} S_{0} = \frac{2}{7} m g sin α_{0} \end{matrix}

érték, és ugyanekkor az (5) egyenletből

\begin{matrix} v_{0}^{2} = \frac{10}{7} R g (1 - cos α_{0}), \end{matrix}

a következő egyismeretlenes (transzcendens) egyenletet kapjuk:

\begin{matrix} 3 cos α = 2 cos α_{0} - \frac{2}{7} sin α_{0} (α - α_{0}) + \frac{10}{7} (1 - cos α_{0}), \end{matrix}

(ahol

α

radiánban értendő). Válasszuk a súrlódási együtthatót

μ = 0, 76

-nak, akkor a konstansok értékei:

α_{0} = 45, 66^{\circ}, sin α_{0} = 0,7152, cos α_{0} = 0,6989,

amivel egyenletünk így alakul:

\begin{matrix} 3 cos α = 2 cos 45, 66^{\circ} - \frac{2}{7} sin 45, 66^{\circ} (α - 45, 66^{\circ}) + \frac{10}{7} - \frac{10}{7} cos 45, 66^{\circ} . \end{matrix}

α

értékét fokban kívánjuk beírni, ez radiánra átszámítva

π / 180

-nal szorzandó, ezzel (a műveletek elvégzése után) a

\begin{matrix} cos α = 0, 66359893 - 1, 18882682 \cdot 10^{- 3} α (fokban) \end{matrix}

egyenlethez jutunk. (A számértékek

9

jegy pontosságát csak az elviek miatt tartottuk meg átmenetileg.) Rövid próbálkozás után (csak a

45, 66^{\circ} < α < 54^{\circ}

szögekkel kell próbálkozni):

α = 53, 0959^{\circ} \approx 53, 1^{\circ}

eredményt kapjuk.
Ebben az eredményben a lineáris közelítés bizonytalansága benne van, ezért az

53, 1^{\circ}

-ot fogadjuk el. Örömmel látjuk, hogy az eredeti megoldásban közölt

53, 96^{\circ}

-os értéktől csak kicsit térünk el, vagyis a megcsúszás figyelmen kívül hagyása durván

\begin{matrix} \frac{53, 96 - 53,1}{53, 1} \approx 1, 6 % \end{matrix}

hibát okozott.