Cím:	Megoldásvázlatok a 2015/2. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Lorántfy László
Füzet:	2015/március, 132 - 138. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Számítsuk ki az $A$ kifejezés pontos értékét: $\begin{array}{c}{\displaystyle A={\left(\sqrt[]{\frac{4-2\sqrt[]{3}}{4+2\sqrt[]{3}}}+\sqrt[]{\frac{5-2\sqrt[]{6}}{5+2\sqrt[]{6}}}\right)}^{-2}\cdot {\left(14-\sqrt[]{12}-\sqrt[]{96}\right)}^2\cdot {\left(\frac{2^2}{2015}\right)}^{-1}\mathrm{.}}\end{array}$  (11 pont)   Megoldás. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{4-2\sqrt[]{3}}{4+2\sqrt[]{3}}}& {\displaystyle =\frac{2-\sqrt[]{3}}{2+\sqrt[]{3}}=\frac{{\left(2-\sqrt[]{3}\right)}^2}{4-3}={\left(2-\sqrt[]{3}\right)}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{5-2\sqrt[]{6}}{5+2\sqrt[]{6}}}& {\displaystyle =\frac{{\left(5-2\sqrt[]{6}\right)}^2}{25-24}={\left(5-2\sqrt[]{6}\right)}^2\mathrm{.}}\hfill \end{array}}$ ${\displaystyle \begin{array}{cc}\hfill {\displaystyle A}& {\displaystyle ={\left(2-\sqrt[]{3}+5-2\sqrt[]{6}\right)}^{-2}\cdot 2^2{\left(7-\sqrt[]{3}-2\sqrt[]{6}\right)}^2\cdot \frac{2015}{2^2}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={\left(7-\sqrt[]{3}-2\sqrt[]{6}\right)}^{-2}\cdot {\left(7-\sqrt[]{3}-2\sqrt[]{6}\right)}^2\cdot 2015=2015.}\hfill \end{array}}$   2. Egy sakkversenyen mindenki mindenkivel egy mérkőzést játszik. Eddig $25$ játszmát fejeztek be, és mindenkinek még hátravan $4$ játszmája. Hány sakkozó vesz részt a versenyen?  (12 pont)   Megoldás. Legyen a részvevők száma $n$, így mindenki $n-1$ mérkőzést játszik. Ha minden sakkozónak még 4 mérkőzése van hátra, akkor eddig mindenki $n-1-4=n-5$ mérkőzést játszott. Ez összesen $\frac{n\left(n-5\right)}{2}$ mérkőzés. Tehát az $\frac{n\left(n-5\right)}{2}=25$ egyenletet kell megoldanunk. Az $n^2-5n-50=0$ másodfokú egyenlet pozitív megoldása $n=10$. Tehát 10 sakkozó vesz részt a versenyen.   3. Oldjuk meg az alábbi egyenletet a valós számok halmazán: $\begin{array}{c}{\displaystyle \frac{{625}^x-{81}^x}{{375}^x+{135}^x}=\frac{2}{\sqrt[]{15}}\mathrm{.}}\end{array}$  (14 pont)   Megoldás. A hatványalapokat bontsuk prímtényezők szorzatára, ezután az egyenlet: $\begin{array}{c}{\displaystyle \frac{{\left(5^x\right)}^4-{\left(3^x\right)}^4}{{\left(5^x\right)}^3\cdot 3^x+{\left(3^x\right)}^3\cdot 5^x}=\frac{2}{\sqrt[]{15}}\mathrm{.}}\end{array}$ Vezessük be az $a=5^x$ és ${b=3}^x$ új változókat, ekkor $\begin{array}{c}{\displaystyle \frac{a^4-b^4}{a^3\cdot b+b^3\cdot a}=\frac{2}{\sqrt[]{15}}\mathrm{.}}\end{array}$ Szorzattá alakítva a számlálót és a nevezőt, majd egyszerűsítve ${(a}^2+b^2\ne 0)$: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{\left(a^2-b^2\right)\left(a^2+b^2\right)}{ab\left(a^2+b^2\right)}}& {\displaystyle =\frac{2}{\sqrt[]{15}}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{a^2-b^2}{ab}}& {\displaystyle =\frac{2}{\sqrt[]{15}}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{a}{b}-\frac{b}{a}}& {\displaystyle =\frac{2}{\sqrt[]{15}}\mathrm{.}}\hfill \end{array}}$ Az $y=\frac{a}{b}=(\frac{5}{3}{)}^x$ új változót bevezetve: $y-\frac{1}{y}=\frac{2}{\sqrt[]{15}}$, $\sqrt[]{15}y$-nal $\left(y\ne 0\right)$ beszorozva a $\sqrt[]{15}{y}^2-2y-\sqrt[]{15}=0$ másodfokú egyenletet kapjuk. Az egyenlet megoldásai: $y_1=-\frac{3}{\sqrt[]{15}}$ és $y_2=\frac{\sqrt[]{5}}{\sqrt[]{3}}$. Az első, negatív megoldás nem lehet pozitív szám hatványa, így a második megoldásból kapjuk az eredeti egyenlet egyetlen megoldását: $(\frac{5}{3}{)}^x=(\frac{5}{3}{)}^{\frac{1}{2}}$. Mivel az $x\to (\frac{5}{3}{)}^x$ függvény szigorúan monoton függvény, ezért ebből $x=\frac{1}{2}$ következik.   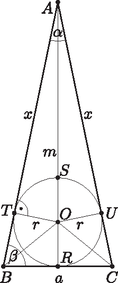4. Egy egyenlő szárú háromszög súlypontja illeszkedik a háromszög beírható körére. Mekkorák a háromszög szögei? Bizonyítsuk be, hogy a beírt kör szárakon lévő két érintési pontja és a szárak közös végpontja három egyenlő részre osztja a háromszög kerületét.  (14 pont)   Megoldás. Az $S$ pont illeszkedik az alaphoz tartozó magasságra és a beírt körre. Mivel a súlypont harmadolja a súlyvonalat, így a magasság harmada egyenlő a kör átmérőjével: $\frac{m}{3}=2r$ vagyis $m=6r$.     Az $AOT$ derékszögű háromszögben $OT=r$ és $OA=m-r=5r$, vagyis $\text{sin}\frac{\alpha }{2}=\frac{r}{5r}=0\mathrm{,}2$, amiből $\alpha \approx 23\mathrm{,}{7}^{\circ }$, és innen $\beta \approx 78\mathrm{,}{46}^{\circ }$. A szimmetria és az érintőszakaszok egyenlősége miatt $AT=AU=x$, $BT=BR=CR=CU=\frac{a}{2}$. A feladat második részének bizonyításához írjuk fel a háromszög területét kétféleképpen: $\begin{array}{c}{\displaystyle T_{ABC▵}=\frac{a\cdot m}{2}=\frac{a\cdot 6r}{2}=3ar\mathrm{,}}\end{array}$ másrészt $\begin{array}{c}{\displaystyle T_{ABC▵}=2T_{ATO▵}+4T_{BRO▵}=2\cdot \frac{x\cdot r}{2}+4\cdot \frac{a\cdot r}{4}=xr+ar\mathrm{.}}\end{array}$ A kettőt egyenlővé téve kapjuk, hogy $3ar=xr+ar$, vagyis $2ar=xr$, amiből következik, hogy $2a=x$. A háromszög kerülete: $\begin{array}{c}{\displaystyle K_{ABC▵}=2x+4\cdot \frac{a}{2}=2x+2a=3x\mathrm{.}}\end{array}$ Mivel $AT=AU=x$, az $A$, $T$ és $U$ pontok valóban harmadolják a háromszög kerületét.   II. rész     5. Vizsgáljuk meg az alábbi egyenlet megoldhatóságát az $m$ paraméter függvényében: $\begin{array}{c}{\displaystyle \text{tg}{}^{2}x+\text{ctg}{}^{2}x+2\text{sin}{}^{2}x+2\text{cos}{}^{2}x+3m^2=4m\left(\text{tg}x+\text{ctg}x\right)\mathrm{.}}\end{array}$  (16 pont)   Megoldás. Ismeretes, hogy $a\ge 0$ esetén $a+\frac{1}{a}\ge 2$, hasonlóan $a\le 0$ esetén $a+\frac{1}{a}\le -2$. Vezessük be az $y=\text{tg}x+\text{ctg}x$ új változót, ekkor $y\le -2$ vagy $2\le y$, valamint $\begin{array}{c}{\displaystyle \text{tg}{}^{2}x+\text{ctg}{}^{2}x+2\text{sin}{}^{2}x+2\text{cos}{}^{2}x=\text{tg}{}^{2}x+\text{ctg}{}^{2}x+2={\left(\text{tg}x+\text{ctg}x\right)}^2=y^2\mathrm{.}}\end{array}$ Az egyenletünk az új változóval: $y^2+3m^2=4my$, rendezve $y^2-4my+3m^2=0$. Az egyenlet diszkriminánsa: $D=16m^2-12m^2=4m^2$, így $D\ge 0$. A megoldóképletet alkalmazva a két megoldás: $\begin{array}{c}{\displaystyle y_{\mathrm{1,2}}=\frac{4m\pm \sqrt[]{16m^2-12m^2}}{2}=2m\pm |m|\mathrm{,}}\end{array}$ ahonnan $y_1=m$ és $y_2=3m$. Nincs megoldása az egyenletnek, ha $m=0$, mert $y=0$ lenne. Ha $0<m$ és $3m<2$, vagyis $m<\frac{2}{3}$, akkor nem lesz megoldás. Hasonlóan, $m<0$ és $-2<3m$, azaz $-\frac{2}{3}<m$ esetén szintén nem lesz megoldás. Tehát nincs megoldása az egyenletnek, ha $-\frac{2}{3}<m<\frac{2}{3}$. Egy megoldást kapunk $y$-ra, ha $0<m<2$ és $2\le 3m$, vagyis $\frac{2}{3}\le m<2$, vagy ha $-2<m<0$ és $3m\le -2$, vagyis $-2<m\le -\frac{2}{3}$. Ilyenkor az eredeti egyenlet megoldásait a $\begin{array}{c}{\displaystyle \text{tg}x+\frac{1}{\text{tg}x}=3m\mathrm{,}\text{azaz a}\text{tg}{}^{2}x-3m\cdot \text{tg}x+1=0}\end{array}$ egyenlet megoldásával kapjuk. Az egyenlet diszkriminánsa $D=9m^2-4\ge 0$, amiből $|m|\ge \frac{2}{3}$, ami az $m$-re adott fenti feltételek esetén teljesül. Ha $m\le -2$ vagy $2\le m$, akkor mindkét $y$-ra kapott értéket visszahelyettesíthetjük, és a megoldásokat a $\text{tg}{}^{2}x-3m\cdot \text{tg}x+1=0$ és a $\text{tg}{}^{2}x-m\cdot \text{tg}x+1=0$ egyenletek gyökei adják. Az egyenletek diszkriminánsát megvizsgálva, az $|m|\ge \frac{2}{3}$ és $|m|\ge 2$ feltételeket kapjuk a megoldhatóságra, melyek az $m$-re adott fenti feltételek esetén teljesülnek.   6. A teafűből a forró vízben a kellemes ízeket adó anyagok gyorsabban kioldódnak, mint a káros csersavak. Előfordul, hogy a teafüvet véletlenül hosszabb ideig hagyjuk a vízben, mint szükséges lenne, ilyenkor a csersavaktól keserű lesz a tea. Az időt percekben mérve, a $t\in \left[\mathrm{0,30}\right]$ intervallumon közelítsük a percenként kioldódó csersav mennyiségét a $v\left(t\right)=-t^3+25t^2+150t$ függvénnyel. Hány százalékkal több csersav oldódik ki a teafűből, ha a szükséges 5 perc helyett $10$ vagy 15 percig benne felejtjük a filtert a vízben?  (16 pont)   Megoldás. Számoljuk ki az 5 perc alatt kioldódó $A$ mennyiséget: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle A}& {\displaystyle ={\int }_0^5-t^3+25t^2+150tdt={\left[-\frac{t^4}{4}+25\cdot \frac{t^3}{3}+150\cdot \frac{t^2}{2}\right]}_0^5\approx }\hfill \\ \hfill {\displaystyle }& {\displaystyle \approx -156\mathrm{,}25+1041\mathrm{,}7+1875=2760\mathrm{,}45.}\hfill \end{array}}$ A 10 perc alatt kioldódó $B$ mennyiség: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle B}& {\displaystyle ={\int }_0^{10}-t^3+25t^2+150tdt={\left[-\frac{t^4}{4}+25\cdot \frac{t^3}{3}+150\cdot \frac{t^2}{2}\right]}_0^{10}\approx }\hfill \\ \hfill {\displaystyle }& {\displaystyle \approx -2500+8333\mathrm{,}3+7500=13333\mathrm{,}3.}\hfill \end{array}}$ A 15 perc alatt kioldódó $C$ mennyiség: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle C}& {\displaystyle ={\int }_0^{15}-t^3+25t^2+150tdt={\left[-\frac{t^4}{4}+25\cdot \frac{t^3}{3}+150\cdot \frac{t^2}{2}\right]}_0^{15}\approx }\hfill \\ \hfill {\displaystyle }& {\displaystyle \approx -12656\mathrm{,}25+28125+16875=32343\mathrm{,}75.}\hfill \end{array}}$ Ha 10 percre felejtjük a vízben a teafüvet, akkor $\begin{array}{c}{\displaystyle \frac{B-A}{A}=\frac{13333\mathrm{,}3-2760\mathrm{,}45}{2760\mathrm{,}45}\approx 3\mathrm{,}83=383\%\text{-kal}}\end{array}$ több, ha pedig 15 percig, akkor $\begin{array}{c}{\displaystyle \frac{C-A}{A}=\frac{32343\mathrm{,}75-2760\mathrm{,}45}{2760\mathrm{,}45}\approx 10\mathrm{,}72=1072\%\text{-kal}}\end{array}$ több csersav oldódik ki, mintha betartottuk volna az 5 percet.   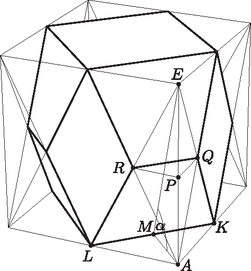7. Egyik lapjára állított 18 cm élhosszúságú kockából kiindulva bonbonos dobozt tervezünk. Az alap és fedőlap oldalfelező pontjait összekötjük a szemközti lap közelebbi csúcsaival, az ábrának megfelelően. A keletkező háromszög alapú gúlákat elhagyjuk a kockából. Az így létrejött testet, a bonbonos dobozt, papírból fogjuk elkészíteni, 30% ragasztási felület, illetve hulladék ráhagyásával. Mennyi papírra lesz szükségünk? Mekkora lesz a doboz térfogata? Mekkora szöget zárnak be a trapéz alakú lapok egymással?  (16 pont)   Megoldás. Vizsgáljuk meg az egyik elhagyott háromszög alapú gúlát, $AKLE$-t, ennek térfogata: $V=\frac{9\cdot 9\cdot 18}{2\cdot 3}=243{\text{cm}}^3$. A $PQRE$ gúla hozzá hasonló, a hasonlóság aránya $\lambda =\frac{1}{2}$, a térfogatuk aránya ${\lambda }^3=\frac{1}{8}$, így az $AKLPQR$ háromszög alapú csonka gúla térfogata $\begin{array}{c}{\displaystyle V_1=\frac{7}{8}V=\frac{1701}{8}\mathrm{.}}\end{array}$ Nyolc darab ilyen csonkagúlát vágunk ki a kockából, így a doboz térfogata $\begin{array}{c}{\displaystyle V_D={18}^3-8\cdot \frac{1701}{8}=4131{\text{cm}}^3\mathrm{.}}\end{array}$     A doboz felszíne két négyzetből, nyolc egyenlő szárú trapézból és nyolc egyenlő szárú háromszögből áll. A négyzet területe: $T_N={\left(9\sqrt[]{2}\right)}^2=162{\text{cm}}^2$. A trapéz alapjai: $9\sqrt[]{2}$ és $\frac{9\sqrt[]{2}}{2}$, szárai $\begin{array}{c}{\displaystyle s=\sqrt[]{9^2+{\left(\frac{9}{2}\right)}^2}=\frac{9\sqrt[]{5}}{2}\mathrm{,}}\end{array}$ magassága: $\begin{array}{c}{\displaystyle m=\sqrt[]{{\left(\frac{9\sqrt[]{5}}{2}\right)}^2-{\left(\frac{9\sqrt[]{2}}{4}\right)}^2}=\frac{27\sqrt[]{2}}{4}\mathrm{.}}\end{array}$ Így a trapéz területe: $\begin{array}{c}{\displaystyle T_T=\frac{9\sqrt[]{2}+\frac{9\sqrt[]{2}}{2}}{2}\cdot \frac{27\sqrt[]{2}}{4}=\frac{729}{8}{\text{cm}}^2\mathrm{.}}\end{array}$ A háromszög területe: $\begin{array}{c}{\displaystyle T_H=\frac{9\cdot 9}{2}=\frac{81}{2}{\text{cm}}^2\mathrm{.}}\end{array}$ A doboz felszíne: $\begin{array}{c}{\displaystyle A=2T_N+8T_T+8T_H=2\cdot 162+8\cdot \frac{729}{8}+8\cdot \frac{81}{2}=324+729+324=1377{\text{cm}}^2\mathrm{.}}\end{array}$ Tehát a ráhagyással együtt $1377{\text{cm}}^2\cdot 1\mathrm{,}3=1790\mathrm{,}1{\text{cm}}^2$ papír szükséges a doboz elkészítéséhez. A $KL$ szakasz felezőpontja legyen az $M$ pont, $AM=\frac{AK}{\sqrt[]{2}}=\frac{9}{\sqrt[]{2}}$. Az $\alpha =AME\sphericalangle$ a trapéz alakú oldal alaplappal bezárt szöge: $\begin{array}{c}{\displaystyle \text{tg}\alpha =\frac{AE}{AM}=\frac{18\sqrt[]{2}}{9}=2\sqrt[]{2}\mathrm{,}\text{amiből}\alpha \approx 70\mathrm{,}{53}^{\circ }\mathrm{.}}\end{array}$ A két trapéz alakú oldallap szöge ennek a szögnek a duplája: $2\alpha \approx 141\mathrm{,}{06}^{\circ }$.   8. Mekkora szögben látszik az alábbi körök közös húrja az origóból? $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle x^2+y^2+4x-2y-20}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle x^2+y^2-8x-8y+22}& {\displaystyle =0.}\hfill \end{array}}}\end{array}$  (16 pont)   Megoldás. Teljes négyzetté alakítás után: $\begin{array}{c}{\displaystyle {\left(x+2\right)}^2+{\left(y-1\right)}^2=25\text{és}{\left(x-4\right)}^2+{\left(y-4\right)}^2=10.}\end{array}$ Ebből leolvasható a két kör középpontja és sugara: $K_1\left(-2;1\right)$, $r_1=5$, $K_2\left(4;4\right)$, $r_2=\sqrt[]{10}$. A két kör egyenletét kivonva egymásból a $12x+6y=42$ egyenletet kapjuk, amiből $y=-2x+7$ következik. Ez a húr egyenesének egyenlete. Ezt visszahelyettesítve az első kör egyenletébe az ${\left(x+2\right)}^2+{\left(-2x+6\right)}^2=25$ másodfokú egyenletet kapjuk. Ennek a megoldásai $x_1=3$, $x_2=1$. Ezeket visszahelyettesítve az egyenes egyenletébe kapjuk, hogy $y_1=1$, $y_2=5$. Tehát a közös húr végpontjainak koordinátái $A\left(1;5\right)$ és $B\left(3;1\right)$. Az $\overrightarrow{OA}$ és $\overrightarrow{OB}$ vektorok szögét kell megadnunk: $\begin{array}{c}{\displaystyle \overrightarrow{OA}\cdot \overrightarrow{OB}=|\overrightarrow{OA}|\cdot |\overrightarrow{OB}|\cdot \text{cos}\gamma =\sqrt[]{26}\cdot \sqrt[]{10}\cdot \text{cos}\gamma \mathrm{.}}\end{array}$ Másrészt a koordinátákból: $\overrightarrow{OA}\cdot \overrightarrow{OB}=3+5=8$. Ezekből $\text{cos}\gamma =\frac{8}{\sqrt[]{260}}\approx 0\mathrm{,}4961$, amiből $\gamma \approx 60\mathrm{,}{26}^{\circ }$.   9. A zöldséges $1$ hetes, $2$ hetes és $3$ hetes narancsokat árul. Annak a valószínűsége, hogy egy $1$ hetes narancs romlott, $0\mathrm{,}01$. Ez a valószínűség a tapasztalatok szerint hetente megduplázódik. A zöldségesnél jelenleg 25 kg $1$ hetes, 17 kg 2 hetes és 6 kg 3 hetes narancs van. A narancsok tömege egyformának tekinthető, 5 db 1 kg. Egyik reggel a pakoláskor összekeveredtek a narancsok. $a)$ Mekkora annak a valószínűsége, hogy egy véletlenszerűen kiválasztott narancs romlott? $b)$ Véletlenszerűen kiválasztottunk egy narancsot, ami jó. Mekkora a valószínűsége, hogy $3$ hetes? $c)$ Vettünk 40 dkg narancsot. Mekkora a valószínűsége, hogy mind jó? És annak, hogy a fele romlott?  (16 pont)   Megoldás. Jelölje $A$, $B$, illetve $C$ rendre azt az eseményt, hogy egy véletlenszerűen kiválasztott narancs 1 hetes, 2 hetes, illetve 3 hetes; $R$ pedig azt az eseményt, hogy egy narancs romlott. Az $A$, $B$ és $C$ események teljes eseményrendszert alkotnak. Adott, hogy $P\left(R|A\right)=0\mathrm{,}01$, $P\left(R|B\right)=0\mathrm{,}02$, $P\left(R|C\right)=0\mathrm{,}04$. Mivel 5 darab narancs 1 kg, ezért 1 hetes narancsból 125, 2 hetesből 85, míg 3 hetesből 30 darab van, ez összesen 240 db narancs. Így a következőket tudjuk még: $\begin{array}{c}{\displaystyle P\left(A\right)=\frac{125}{240}\mathrm{,}P\left(B\right)=\frac{85}{240}\text{és}P\left(C\right)=\frac{30}{240}\mathrm{.}}\end{array}$ $a)$ A teljes valószínűség tételét használva: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P\left(R\right)}& {\displaystyle =P\left(A\right)P\left(R|A\right)+P\left(B\right)(P\left(R|B\right)+P\left(C\right)P\left(R|C\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{125}{240}\cdot 0\mathrm{,}01+\frac{85}{240}\cdot 0\mathrm{,}02+\frac{30}{240}\cdot 0\mathrm{,}04\approx 0\mathrm{,}0173.}\hfill \end{array}}$ $b)$ ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P\left(C|\overline{R}\right)}& {\displaystyle =\frac{P\left(C\overline{R}\right)}{P\left(\overline{R}\right)}=\frac{P\left(C\right)P\left(\overline{R}|C\right)}{P\left(\overline{R}\right)}=\frac{P\left(C\right)\left(1-P\left(R|C\right)\right)}{1-P\left(R\right)}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{\frac{30}{240}\cdot \left(1-0\mathrm{,}04\right)}{1-0\mathrm{,}0173}\approx 0\mathrm{,}1221.}\hfill \end{array}}$ $c)$ Felhasználjuk, hogy $P\left(\overline{R}|A\right)=1-P\left(R|A\right)=0\mathrm{,}99$, $P\left(\overline{R}|B\right)=1-P\left(R|B\right)=0\mathrm{,}98$ és $P\left(\overline{R}|C\right)=1-P\left(R|C\right)=0\mathrm{,}96$. A két narancs kiválasztására a következő lehetőségek vannak: mindkettő 1 hetes; mindkettő 2 hetes; mindkettő 3 hetes; egyik 1, másik 2 hetes; egyik 1, másik 3 hetes; egyik 2, másik 3 hetes. ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle P\left(\text{mindkét narancs jó}\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =}\hfill & {\displaystyle \frac{\left(\genfrac{}{}{0ex}{}{125}{2}\right)}{\left(\genfrac{}{}{0ex}{}{240}{2}\right)}\cdot P{\left(\overline{R}\mid A\right)}^2+\frac{\left(\genfrac{}{}{0ex}{}{85}{2}\right)}{\left(\genfrac{}{}{0ex}{}{240}{2}\right)}\cdot P{\left(\overline{R}\mid B\right)}^2+\frac{\left(\genfrac{}{}{0ex}{}{30}{2}\right)}{\left(\genfrac{}{}{0ex}{}{240}{2}\right)}\cdot P{\left(\overline{R}\mid C\right)}^2+}\hfill \\ \hfill {\displaystyle }& {\displaystyle +}\hfill & {\displaystyle \frac{125\cdot 85}{\left(\genfrac{}{}{0ex}{}{240}{2}\right)}\cdot P\left(\overline{R}\mid A\right)\cdot P\left(\overline{R}\mid B\right)+\frac{125\cdot 30}{\left(\genfrac{}{}{0ex}{}{240}{2}\right)}\cdot P\left(\overline{R}\mid A\right)\cdot P\left(\overline{R}\mid C\right)+}\hfill \\ \hfill {\displaystyle }& {\displaystyle +}\hfill & {\displaystyle \frac{85\cdot 30}{\left(\genfrac{}{}{0ex}{}{240}{2}\right)}\cdot P\left(\overline{R}\mid B\right)\cdot P\left(\overline{R}\mid C\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =}\hfill & {\displaystyle \frac{1}{240\cdot 239}\cdot \left(125\cdot 124\cdot 0\mathrm{,}{99}^2+85\cdot 84\cdot 0\mathrm{,}{98}^2+30\cdot 29\cdot 0\mathrm{,}{96}^2\right)+}\hfill \\ \hfill {\displaystyle }& {\displaystyle +}\hfill & {\displaystyle \frac{1}{240\cdot 239}\cdot \left(2\cdot 125\cdot 85\cdot 0\mathrm{,}99\cdot 0\mathrm{,}98+2\cdot 125\cdot 30\cdot 0\mathrm{,}99\cdot 0\mathrm{,}96+2\cdot 85\cdot 30\cdot 0\mathrm{,}98\cdot 0\mathrm{,}96\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =}\hfill & {\displaystyle \frac{55393\mathrm{,}428}{240\cdot 239}\approx 0\mathrm{,}9657.}\hfill \end{array}}$ A másik kérdésre a választ hasonló gondolatmenettel kapjuk meg: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle P\left(\text{a fele narancs jó}\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =}\hfill & {\displaystyle \frac{\left(\genfrac{}{}{0ex}{}{125}{2}\right)}{\left(\genfrac{}{}{0ex}{}{240}{2}\right)}\cdot 0\mathrm{,}99\cdot 0\mathrm{,}01+\frac{\left(\genfrac{}{}{0ex}{}{85}{2}\right)}{\left(\genfrac{}{}{0ex}{}{240}{2}\right)}\cdot 0\mathrm{,}98\cdot 0\mathrm{,}02+\frac{\left(\genfrac{}{}{0ex}{}{30}{2}\right)}{\left(\genfrac{}{}{0ex}{}{240}{2}\right)}\cdot 0\mathrm{,}96\cdot 0\mathrm{,}04+}\hfill \\ \hfill {\displaystyle }& {\displaystyle +}\hfill & {\displaystyle \frac{125\cdot 85}{\left(\genfrac{}{}{0ex}{}{240}{2}\right)}\cdot \left(0\mathrm{,}99\cdot 0\mathrm{,}02+0\mathrm{,}01\cdot 0\mathrm{,}98\right)+\frac{125\cdot 30}{\left(\genfrac{}{}{0ex}{}{240}{2}\right)}\cdot \left(0\mathrm{,}99\cdot 0\mathrm{,}04+0\mathrm{,}01\cdot 0\mathrm{,}96\right)+}\hfill \\ \hfill {\displaystyle }& {\displaystyle +}\hfill & {\displaystyle \frac{85\cdot 30}{\left(\genfrac{}{}{0ex}{}{240}{2}\right)}\cdot \left(0\mathrm{,}98\cdot 0\mathrm{,}04+0\mathrm{,}02\cdot 0\mathrm{,}96\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =}\hfill & {\displaystyle \frac{\mathrm{1622,642}}{240\cdot 239}\approx 0\mathrm{,}0283.}\hfill \end{array}}$