Cím:	Megoldásvázlatok a 2015/1. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Székely Péter
Füzet:	2015/február, 74 - 80. oldal	PDF  |  MathML

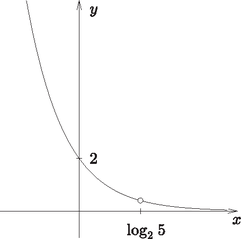
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Ábrázoljuk és jellemezzük az alábbi függvényt a lehető legbővebb számhalmazon: $\begin{array}{c}{\displaystyle f:x\mapsto \left(\frac{2^x+5}{2^{x+1}-10}-\frac{2^x-5}{2^{x+1}+10}-\frac{50}{25-4^x}\right):\frac{5\cdot 2^x}{2^x-5}\mathrm{.}}\end{array}$ (11 pont)   Megoldás. Legyen $a=2^x$. Ekkor a megfelelő feltételek mellett ($a>0$ és $a\ne 5$, vagyis $x\ne \text{log}{}_{2}5$): ${\displaystyle \begin{array}{c}\hfill {\displaystyle \left(\frac{a+5}{2a-10}-\frac{a-5}{2a+10}-\frac{50}{25-a^2}\right):\frac{5a}{a-5}=}\hfill \\ \hfill {\displaystyle =\frac{{\left(a+5\right)}^2-{\left(a-5\right)}^2+100}{2\left(a-5\right)\left(a+5\right)}\cdot \frac{a-5}{5a}=\frac{20a+100}{2\left(a+5\right)}\cdot \frac{1}{5a}=\frac{2}{a}\mathrm{.}}\hfill \end{array}}$     Az ábrázolandó függvény tehát $\begin{array}{c}{\displaystyle f:x\mapsto \frac{2}{2^x}={\left(\frac{1}{2}\right)}^{x-1}\mathrm{.}}\end{array}$ Jellemzése: ‐ $D_f=\text{R}\setminus \left\{\text{log}{}_{2}5\right\}$, ‐ $R_f={\text{R}}^{+}\setminus \left\{\frac{2}{5}\right\}$, ‐ nullahelye nincs, ‐ tengelymetszete $y=2$-nél, ‐ szigorúan monoton csökkenő $x\in D_f$-en, ‐ konvex.   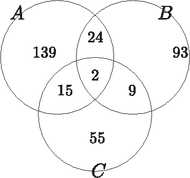2. Mennyi a valószínűsége, hogy a háromjegyű pozitív egészek közül találomra olyat választunk, mely az $5$, a $7$, illetve a $11$ egyikével sem osztható?  (12 pont)   Megoldás. $9\cdot 10\cdot 10=900$ háromjegyű szám van. Legyen $A$ az 5-tel, $B$ a 7-tel és $C$ a 11-gyel osztható számok halmaza. Ekkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle |A|}& {\displaystyle =\mathrm{180,}}\hfill \\ \hfill {\displaystyle |B|}& {\displaystyle =\mathrm{128,}}\hfill \\ \hfill {\displaystyle |C|}& {\displaystyle =\mathrm{81,}}\hfill \\ \hfill {\displaystyle |A\cap B|}& {\displaystyle =\mathrm{26,}}\hfill \\ \hfill {\displaystyle |A\cap C|}& {\displaystyle =\mathrm{17,}}\hfill \\ \hfill {\displaystyle |B\cap C|}& {\displaystyle =11\text{ és}}\hfill \\ \hfill {\displaystyle |A\cap B\cap C|}& {\displaystyle =2.}\hfill \end{array}}$     A 7-tel, vagy 11-gyel, vagy 13-mal oszthatók száma (a logikai szita módszere szerint): $\begin{array}{c}{\displaystyle |A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|=337.}\end{array}$ Tehát a keresett valószínűség: $\begin{array}{c}{\displaystyle p=\frac{\text{jó esetek száma}}{\text{összes eset}}=\frac{563}{900}=0\mathrm{,}626.}\end{array}$   3. Matematikus barátunk statisztikát csinál a kiránduláson készített $500$ fényképéről. Azt találja, hogy a méretük átlaga 2,84 MB, s a legnagyobb méretű képe 3,65 MB-os. $a)$ Mennyi a méretük szórásának legkisebb értéke? $b)$ Legfeljebb mekkora lehet a méretük szórása, ha a terjedelem 1,62 MB?  (14 pont)   Megoldás. $a)$ A szórás legkisebb értéke ugyanott van, ahol a négyzetéé. Így $D^2$ minimumát keressük, s a számtani és kvadratikus közepek közötti egyenlőtlenséggel adjuk meg azt: $\begin{array}{c}{\displaystyle D^2=\frac{{\left(3\mathrm{,}65-2\mathrm{,}84\right)}^2+\sum _{i=1}^{499}{\left(2\mathrm{,}84-x_i\right)}^2}{500}\mathrm{.}}\end{array}$ Ekvivalens átalakításokkal: $\begin{array}{c}{\displaystyle 500D^2-{\left(3\mathrm{,}65-2\mathrm{,}84\right)}^2=\sum _{i=1}^{499}{\left(2\mathrm{,}84-x_i\right)}^2\mathrm{.}}\end{array}$ A jobb oldalra felírva a számtani-kvadratikus közepek közötti egyenlőtlenséget: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\sum }_{i=1}^{499}{\left(2\mathrm{,}84-x_i\right)}^2}& {\displaystyle =499{\left(\sqrt[]{\frac{{\sum }_{i=1}^{499}{\left(2\mathrm{,}84-x_i\right)}^2}{499}}\right)}^2\ge 499{\left(\frac{{\sum }_{i=1}^{499}|\mathrm{2,84}-x_i|}{499}\right)}^2\ge }\hfill \\ \hfill {\displaystyle }& {\displaystyle \ge 499{\left(\frac{{\sum }_{i=1}^{499}\left(2\mathrm{,}84-x_i\right)}{499}\right)}^2\ge 499{\left(\frac{499\cdot \mathrm{2,84}-{\sum }_{i=1}^{499}{x}_i}{499}\right)}^2\mathrm{.}}\hfill \end{array}}$ A kapott kifejezés értéke konstans, hiszen a ${\sum }_{i=1}^{499}{x}_i$ a maradék 499 elem összege, $500\cdot 2\mathrm{,}84-3\mathrm{,}65$. Ez azt jelenti, hogy a bal oldalon lévő kifejezés értéke legalább ekkora, s az egyenlőség akkor áll fenn, ha minden maradék elem ugyanakkora és legfeljebb 2,84. Legyen ez az érték $x^{*}$. Ekkor az átlagra igaz, hogy $2\mathrm{,}84=\frac{499x^{*}+3\mathrm{,}65}{500}$, amiből $x^{*}=2\mathrm{,}8384<2\mathrm{,}84$. Tehát a szórás $x^{*}=2\mathrm{,}8384$ esetén lesz a legkisebb, s ez a minimális érték $D=0\mathrm{,}036$. $b)$ A legnagyobb szórás akkor lesz, ha minden kép mérete a legtávolabb van az átlagtól. Miután a legnagyobb 3,65 MB-os, ebből kell 250 darab, s 250 darab kell abból a méretből, mely az ellenkező irányban tér el ugyanennyit az átlagtól. 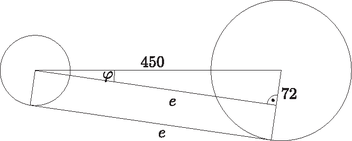Ekkor a szórás: $\begin{array}{c}{\displaystyle D=\sqrt[]{\frac{250\cdot {\left(x_{\underset{}{\overset{}{\text{max}}}}-\overline{x}\right)}^2+250\cdot {\left(\overline{x}-x_{\underset{}{\overset{}{\text{min}}}}\right)}^2}{500}}=\sqrt[]{\frac{500{\left(3\mathrm{,}65-2\mathrm{,}84\right)}^2}{500}}=3\mathrm{,}65-2\mathrm{,}84=0\mathrm{,}81.}\end{array}$   4. A fixhajtású kerékpárnál fontos a lánc feszessége. Az első lánckerék sugara 104 mm, fogszáma $52$, a hátsó lánckerék adatai pedig 32 mm és 16 fog. (A lánckerék sugarát úgy mértük, hogy az megegyezik egy, a lánckerékre illeszkedő láncszem középpontjának a lánckerék középpontjától mért távolságával.) Milyen hosszú láncra van szükségünk, ha a két lánckerék középpontjának távolsága 450 mm? Hány láncszemet tartalmaz ez a lánc?  (14 pont)   Megoldás. Az érintőszakasz hossza: $e=\sqrt[]{{450}^2-{72}^2}=444\mathrm{,}2$ mm. $\begin{array}{c}{\displaystyle \phi =\text{arcsin}\frac{72}{450}\approx 9\mathrm{,}{207}^{\circ }\mathrm{.}}\end{array}$         A középponti szögek tételét felhasználva (miszerint az ívek aránya egy adott körben megegyezik a hozzájuk tartozó középponti szögek arányával): ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{k_1}{2\cdot 32\cdot \pi }=\frac{{180}^{\circ }-2\phi }{{360}^{\circ }}}& {\displaystyle \Rightarrow k_1\approx 90\mathrm{,}25\text{ mm,}}\hfill \\ \hfill {\displaystyle \frac{k_2}{2\cdot 104\cdot \pi }=\frac{{180}^{\circ }+2\phi }{{360}^{\circ }}}& {\displaystyle \Rightarrow k_2\approx 360\mathrm{,}15\text{ mm.}}\hfill \end{array}}$ Így a teljes lánc hossza: $l=k_1+k_2+2e\approx 1338\mathrm{,}8$ mm. Egy láncszem hossza: $\frac{2\cdot 104\cdot \pi }{52}\approx 12\mathrm{,}566$ mm. Így a láncszemek számára $n\approx \frac{1338\mathrm{,}8}{12\mathrm{,}566}\approx 106\mathrm{,}54$-et kapunk. Tehát legalább 107 láncszemre van szükségünk.   II. rész     5. Milyen $m\in \text{R}$ paraméter esetén lesz hegyesszögű $\alpha$ megoldása a következő egyenletnek? $\begin{array}{c}{\displaystyle \text{cos}{}^2\alpha -\left(18-2m\right)\text{cos}\alpha +m^2+3m+3=0}\end{array}$ (16 pont)   Megoldás. Ahhoz, hogy legyen gyök, $D\ge 0$-nak kell teljesülnie: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(18-2m\right)}^2-4\cdot 1\cdot \left(m^2+3m+3\right)}& {\displaystyle \ge \mathrm{0,}}\hfill \\ \hfill {\displaystyle 324-72m-12m-12}& {\displaystyle \ge \mathrm{0,}}\hfill \\ \hfill {\displaystyle \frac{26}{7}}& {\displaystyle \ge m\mathrm{.}}\hfill \end{array}}$ Ahhoz, hogy pozitív gyöke legyen ($\alpha$ akkor hegyesszögű, ha $\text{cos}\alpha >0$), mivel $x_1\cdot x_2>0$ ($m^2+3m+3>0$ igaz állítás), az $x_1+x_2>0$ egyenlőtlenségnek kell teljesülnie. Ebből ismét a ViŠte-formulák felhasználásával az  $m<9$ feltételt kapjuk. A koszinusz függvény maximális értéke 1, s a feltétel miatt 1 sem lehet ($\alpha$ hegyesszög, így a $0^{\circ }$ érték nem lehetséges). Emiatt a $\text{cos}\alpha <1$ feltételnek is fenn kell állnia. A $\begin{array}{c}{\displaystyle \frac{18-2m\pm \sqrt[]{312-84m}}{2}<1}\end{array}$ egyenlőtlenségből a $\begin{array}{c}{\displaystyle \pm \sqrt[]{78-21m}<m-8}\end{array}$ egyenlőtlenséget kapjuk. A korábbi feltételek miatt ennek a jobb oldala negatív, tehát a bal oldalon lévő kifejezésnél is csak a negatív érték lehetséges. A négyzetre emelés során a relációjel megfordul: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 78-21m}& {\displaystyle >m^2-16m+\mathrm{64,}}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle >\left(m+7\right)\left(m-2\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle -7}& {\displaystyle <m<2.}\hfill \end{array}}$ A feltételek alapján a megoldás: $\begin{array}{c}{\displaystyle \underset{-7<m<2}{\overset{}{\underbrace{m\le \frac{26}{7}\text{ és }m<9\text{ és }-7<m<2}}}\mathrm{.}}\end{array}$   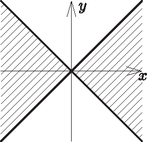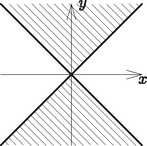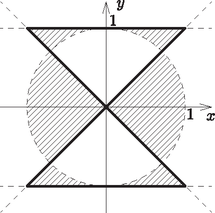6. Ábrázoljuk a következő ponthalmazt a koordinátasíkon: $\begin{array}{c}{\displaystyle H:=\left\{P\left(x;y\right)|\frac{x^2-y^2}{x^2+y^2-1}\le 0\wedge |y|\le 1\right\}}\end{array}$ Mekkora a ponthalmaz területe?  (16 pont)   Megoldás. A nevezőben lévő kifejezés az origó középpontú egységkör egyenletére emlékeztet. Emiatt a következő eseteket érdemes megvizsgálni: $a)$ a körön belüli pontokról, vagy $b)$ a körön kívüli pontokról van szó. $a)$ Ha a nevező negatív, vagyis az origó középpontú egységkörön belüli pontokról van szó, akkor a számlálónak nem-negatívnak kell lennie. Ekkor az $x^2\ge y^2$ áll fenn. E második feltételnek az ábrán látható pontok tesznek eleget.     $b)$ Ha a nevező pozitív, vagyis az origó középpontú egységkörön kívüli pontokról van szó, akkor a számlálónak negatívnak kell lennie. Ekkor az $x^2\le y^2$ áll fenn. E második feltételnek az ábrán látható pontok tesznek eleget.     A két fenti esetet, az egységkört, valamint az $|y|\le 1$ feltételeket összevetve a következő ponthalmazt kapjuk:     A két negyedkör-cikk területéhez hozzáadva a négy kis szögletet kapjuk a keresett területet: $\begin{array}{c}{\displaystyle T=2\cdot \frac{1^2\pi }{4}+4\cdot \left[\frac{1\cdot 1}{2}-\frac{1^2\pi }{8}\right]=\frac{\pi }{2}+2-\frac{\pi }{2}=2.}\end{array}$   7. 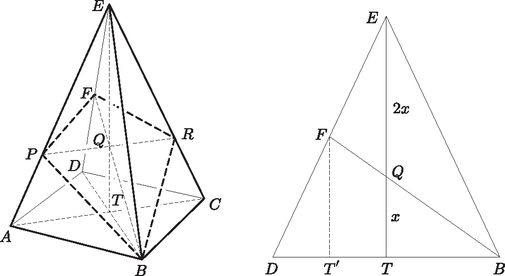Az $ABCD$ négyzet alapú egyenes gúla $AE$ odalalélének $P$ pontjára teljesül, hogy $AP:PE=1:2$, valamint a $CE$ oldalélének $R$ pontjára igaz, hogy $CR:RE=1:2$. $a)$ Milyen arányban osztja a $B$ csúcson, valamint a $P$ és $R$ pontokon átmenő sík a $DE$ élt? $b)$ Hány százaléka a keletkező síkmetszet területe az alap négyzetlap területének, ha a gúla magassága az alaplap átlójának másfélszerese?  (16 pont)   Megoldás. $a)$ Mivel az $ABCDE$ egyenes gúla, a $PR$ szakasz a magasságot a $Q$ harmadolópontban metszi. Vegyük a gúla $DBE$ síkmetszetét. A $DBE$ háromszögben a $TE$ súlyvonalat a $Q$ pont $1:2$ arányban osztja, tehát $Q$ súlypont. Így a $BQ$ meghosszabbítása a $DE$ oldalt az $F$ felezőpontban metszi (szintén súlyvonal).     $b)$ Az egyenes gúla szimmetriája miatt $BF\perp PR$, a síkmetszet deltoid. Területét az átlók segítségével számoljuk ki. A $PR$ szakasz az $AC$  $2/3$-ad része, valamint a $T\text{'}$ pont felezi az $TD$ szakaszt (párhuzamos szelők tétele). A feltétel szerint $TE=3x=\frac{3}{2}DB$, tehát $TB=x$, amiből következik, hogy $\alpha ={45}^{\circ }$. Innen $\begin{array}{c}{\displaystyle \frac{T_{BRFP}}{T_{ABCD}}=\frac{\frac{PR\cdot BF}{2}}{\frac{AC\cdot BD}{2}}=\frac{\frac{2}{3}AC\cdot \sqrt[]{2}BT\text{'}}{AC\cdot BD}=\frac{\frac{2}{3}AC\cdot \sqrt[]{2}\cdot \frac{3}{4}BD}{AC\cdot BD}=\frac{\sqrt[]{2}}{2}\mathrm{.}}\end{array}$ Tehát a $BRFP$ négyszög területe kb. 70,7%-a az alaplap területének.   8. Készítsünk ,,mérőhengert'', mely az $f\left(x\right)=x^{10}$, ahol $x\in \left[-1;1\right]$ függvény $y$ tengely körüli megforgatásával jön létre. A koordinátarendszer egységeit dm-ben mérjük. Készítsünk deciliterenként beosztást az oldalán. (Milyen magasságoknál lesznek az osztásvonalak?)  (16 pont)   Megoldás. Az egyszerűbb számolás kedvéért döntsük meg a mérőedényt ${90}^{\circ }$-kal. Így a megadott $f\left(x\right)=x^{10}$ függvény helyett annak inverzét, a $g\left(x\right)=\sqrt[10]{x}$ függvényt kell az $x$ tengely körül megforgatnunk. A megforgatott függvény $h_i$ intervallumhatárait kell úgy meghatározni, hogy a keletkező szeletek térfogata 1 legyen: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\int }_0^{h_1}g\left(x\right)dx={\int }_0^{h_1}{\left(\sqrt[10]{x}\right)}^2\pi dx}& {\displaystyle =1}\hfill \\ \hfill {\displaystyle \pi {\int }_0^{h_1}{x}^{\frac{1}{5}}dx}& {\displaystyle =\mathrm{1,}}\hfill \\ \hfill {\displaystyle \frac{5}{6}\pi {\left[x^{\frac{6}{5}}\right]}_0^{h_1}}& {\displaystyle =\mathrm{1,}}\hfill \\ \hfill {\displaystyle \frac{5}{6}\pi {h_1}^{\frac{6}{5}}}& {\displaystyle =\mathrm{1,}}\hfill \\ \hfill {\displaystyle h_1\approx 0\mathrm{,}4484}& {\displaystyle \text{ (dm)}\mathrm{.}}\hfill \end{array}}$     Hasonlóképpen az integrált 2-ig számolva kaphatjuk a $h_2\approx 0\mathrm{,}7990\text{(dm)}$ értéket. A következő osztás már nem fér az edény oldalára.   9. Egy ,,piramisjáték'' elindítója a második hétre már $4$ embert sikeresen beszervezett, így öten lettek. (Az első hét a tervezés ideje volt.) A szervezés olyan jól sikerült, hogy a harmadik héttől kezdve minden héten a következő sorozat szerint alakult az összes résztvevő száma: $a_n=3a_{n-1}-8$. $a)$ Hányan vettek részt az ötödik héten a játékban? $b)$ Mutassuk meg, hogy az összes résztvevők száma monoton növekvő sorozatot alkot. $c)$ Írjuk fel explicit alakban a sorozatot. $d)$ Igazoljuk, hogy a sorozat utolsó számjegyei $n=2$-től kezdve periodikus sorozatot alkotnak.  (16 pont)   Megoldás. $a)$ Helyettesítsük be az egymást követő értékeket az adott rekurzív képletbe: ${\displaystyle \begin{array}{cccc}\hfill {\displaystyle a_2}& {\displaystyle =\mathrm{5,}}\hfill & {\displaystyle a_3}\hfill & \hfill {\displaystyle =3\cdot 5-8=\mathrm{7,}}\\ \hfill {\displaystyle a_4}& {\displaystyle =3\cdot 7-8=\mathrm{13,}}\hfill & {\displaystyle a_5}\hfill & \hfill {\displaystyle =3\cdot 13-8=31.}\end{array}}$ $b)$ $a_n$ akkor monoton növekedő, ha $3\cdot a_{n-1}-8\ge a_{n-1}$, azaz $2a_{n-1}\ge 8$ teljesül $\forall n\in {\text{N}}^{+}\setminus \left\{1\right\}$ esetén. Ezt teljes indukcióval tesszük meg: $\left(i\right)$ Belátható, hogy az első elemekre teljesül: $10\ge 8$, $14\ge 8$, $\text{...}$ . $\left(ii\right)$ Tegyük fel, hogy egy tetszőleges $\left(k-1\right)$-dik elemre teljesül az állítás, azaz $2a_{k-1}\ge 8$, ahol $k>2$. $\left(iii\right)$ Belátjuk, hogy a következő elemre, $a_k$-ra is teljesül az állítás: $\begin{array}{c}{\displaystyle 2a_{k}6a_{k-1}-16=3\cdot \left(2a_{k-1}\right)-1624-16=8.}\end{array}$ Tehát a sorozat valóban monoton növekedő. $c)$ Írjuk fel az egyes elemek részletes kiszámítását: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a_4}& {\displaystyle =3\cdot \left(3\cdot 5-8\right)-\mathrm{8,}}\hfill \\ \hfill {\displaystyle a_5}& {\displaystyle =3\cdot \left(3\cdot \left(3\cdot 5-8\right)-8\right)-\mathrm{8,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle ⋮}\hfill \\ \hfill {\displaystyle a_n}& {\displaystyle =3^{n-2}\cdot 5-8\cdot \left(3^{n-3}+3^{n-4}+\text{...}+3^0\right)\mathrm{.}}\hfill \end{array}}$ Felhasználva a mértani sorozat első $n$ elemére vonatkozó összegképletet: $\begin{array}{c}{\displaystyle a_n=5\cdot 3^{n-2}-8\cdot \frac{3^{n-2}-1}{3-1}=5\cdot 3^{n-2}-4\cdot 3^{n-2}+4=3^{n-2}+4\left(n\ge 2\right)\mathrm{.}}\end{array}$ $d)$ Írjuk fel az első néhány végződést: 5, 7, 3, 1, 5, $\text{...}$ . A negyedik elem után az ötös végződést kapjuk ismét, amelyen a rekurzió képletét alkalmazva ismét a 7-es végződést kapjuk stb. (A kétjegyű számokat $10N+c$ alakban felírva megmutatható, hogy az egyesek helyiértékén álló jegyen végzett művelet adja az újabb végződést, mely független a többi számjegytől: $3\cdot \left(10N+c\right)-8=\left(3N\right)\cdot 10+\left(3c-8\right)$.)