Cím: A 2014. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása
Szerző(k):  Fleiner Tamás 
Füzet: 2015/február, 68 - 72. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek, Matematika, Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

 
1. Egy n tagú társaság minden tagja legalább egy, de legfeljebb n-2 tagot ismer a többiek közül, az ismeretség mindig kölcsönös. Bizonyítsuk be, hogy a társaság négy alkalmasan választott tagja leültethető egy asztal köré úgy, hogy mindegyikük pontosan egyet ismerjen a két asztalszomszédja közül.
 
1. megoldás. Legyen A a társaság egy olyan tagja, aki a társaságból a lehető legtöbb személyt ismeri. Legyen B egy olyan illető, akit A nem ismer, C pedig legyen B egy ismerőse. Mivel C-nek legfeljebb annyi ismerőse van, mint A-nak, ezért függetlenül attól, hogy A és C ismeri-e egymást, A-nak legalább annyi C-től különböző ismerőse van, mint ahány A-tól különböző ismerőse van C-nek. A konstrukció folytán C ismeri azt a B-t, akit A nem ismer. Ezért A-nak bizonyosan van olyan C-től különböző D ismerőse, akit C nem ismer. Ekkor ha A, B, C és D ebben a sorrendben ülnek az asztalhoz, akkor éppen a feladatban kirótt feltételt teljesítik.  □
 
2. megoldás. Készítsük el az élszínezett G gráfot az n pontú teljes gráfból az alábbiak szerint. A G gráf csúcsait kölcsönösen egyértelműen megfeleltetjük a társaság tagjainak, és G egy éle akkor legyen piros, ha a csúcsoknak megfelelő tagok nem ismerik egymást, egyébként pedig az adott él színe legyen zöld.
A bizonyítandó állítás átfogalmazható úgy, hogy ha a teljes gráf éleit úgy színezzük pirosra és zöldre, hogy minden csúcsból indul piros és zöld él is, akkor a gráfban van tarka négyszög, azaz négy különböző A, B, C és D csúcs úgy, hogy míg az AB és CD élek pirosak, addig a BC és DA élek zöldek. Az alábbiakban ezt az állítást fogjuk n szerinti teljes indukcióval igazolni. Ez az állítás n=1 esetén nyilvánvalóan teljesül, hiszen a feltevés lehetetlent kíván.
Tegyük fel tehát, hogy legfeljebb n-1 csúcsú gráfokra már igazoltuk az indukciós állítást, és a vizsgált G-nek n csúcsa van. Legyen A a G egy csúcsa. Ha az A törlésével keletkező G-A gráf minden csúcsából indul piros és zöld él is, akkor kész vagyunk, hisz az indukciós feltevés miatt G-A-ban van tarka négyszög, ami persze egyúttal G-ben is tarka négyszög. Feltehetjük tehát, hogy G-A egy B csúcsából (mondjuk) csak piros él indul (és persze AB zöld). Ha most G-B-ben nincs tarka négyszög, akkor az indukciós feltevés miatt G-B-ben van olyan C csúcs, amelyből csupa egyszínű él indul.
Ha A=C, akkor a zöld AB élen kívül A-ból és B-ből csak piros élek indulnak. Legyen BX egy piros, XY pedig egy zöld él. Mivel XY zöld, ezért Y≠A, tehát ABXY tarka négyszög. Ha pedig A≠C, akkor legyen AD egy A-ból induló piros él. A konstrukció folytán AB zöld, BC piros, CD zöld és DA piros, tehát ABCD egy G-beli tarka négyszög. Az indukciós állítást ezzel igazoltuk, a bizonyítás ezzel teljes.  □
 
Megjegyzés. Általában nem igaz, hogy egy 4-személyesnél nagyobb asztalhoz is biztosan le tudjuk ültetni a társaság néhány tagját a feladatban leírt módon. Ha ugyanis a társaságban van két olyan ismerős, hogy egyikük se ismeri a társaság egyetlen más tagját sem, továbbá e két ismerősön kívül mindenki mindenkit ismer, akkor teljesül a feladatban kirótt feltétel, de 4-nél több ember nem ültethető le a kívánt módon.

 
2. Legyen ABC hegyesszögű háromszög, és legyen P olyan pont a háromszög belsejében, amely nem illeszkedik a háromszög egyik magasságvonalára sem. Az A, B, illetve C csúcsból induló magasság talppontját jelölje rendre A1, B1, illetve C1. Messék a háromszög köré írt kört az AP, BP, CP félegyenesek rendre az A2, B2, C2 pontokban. Bizonyítsuk be, hogy az AA1A2, BB1B2 és CC1C2 körívek egy ponton mennek át.
 
Megoldás. Jelölje az ABC, AA1A2, BB1B2 és CC1C2 köröket rendre k, ka, kb, illetve kc; az ABC háromszög magasságpontja legyen M. A feltétel szerint az ABC háromszög hegyesszögű, ezért az A1, B1, C1, M pontok k belsejében vannak.
A k kerületén az AA2, BB2 és CC2 pontpárok páronként elválasztják egymást, ezért a ka, kb és kc körök közül bármelyik kettő metszi egymást úgy, hogy az egyik metszéspontjuk k belsejében, a másik metszéspontjuk k-n kívül helyezkedik el. Legyen a ka és a kb körök metszéspontja k belsejében X, a másik metszéspontjuk legyen Y. Azt fogjuk megmutatni, hogy a kc kör is átmegy az X és Y pontok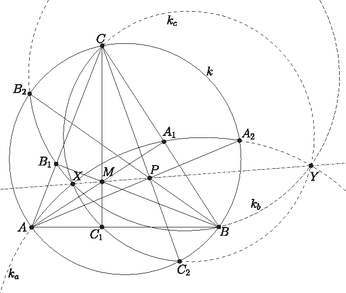on.

 
 

A P pont k-ra vonatkozó hatványa
PA⋅PA2=PB⋅PB2=PC⋅PC2.
Ezek a szorzatok egyben a P hatványai a ka, kb, illetve kc körökre. Tehát a P pontnak a ka, kb és kc körökre vonatkozó hatványa ugyanakkora.
Hasonlóan, az M pontnak az ABA1B1, BCB1C1, CAC1A1 körökre vonatkozó hatványa
MA⋅MA1=MB⋅MB1=MC⋅MC1.
Ezek a szorzatok pedig az M hatványai a ka, kb, illetve kc körökre. Tehát az M pontnak a ka, kb és kc körökre vonatkozó hatványa is ugyanakkora.
A feltétel szerint P és M különböző. Így a PM egyenes a ka, kb és kc körök közös hatványvonala. A három kör tehát egy körsorhoz tartozik, így ka és kb metszéspontjain átmegy kc is.
Ezzel megmutattuk, hogy a ka, kb, illetve kc körök k-n belüli ívei, nevezetesen az AA1A2, BB1B2 és CC1C2 körívek egy ponton mennek át.  □
 

Megjegyzés. Egy alkalmas sztereografikus projekcióval (térbeli inverzióval) visszavezethetjük az állítást arra a jól ismert tényre, hogy a gömbfelületen bármely három körvonal páronként vett hatványvonalai egy átmérőre illeszkednek.
Jelöljük Π-vel az ABC háromszög síkját, és legyen Γ az a gömb, amelynek a k főköre. A P pontban állítsunk merőleges egyenest Π-re; legyen ennek egyik döféspontja a Γ-val O. Invertáljuk az ábrát az O középpontú, P-n átmenő gömbre; a szokásos módon tetszőleges x objektum képét jelöljük x'-vel. Az inverzió jól ismert tulajdonságai szerint a Π sík képe az OP átmérőjű Π' gömb; a Π síkban fekvő körök képei a gömbfelületen fekvő körvonalak. Speciálisan, a BCB1C1, a CAC1A1 és az ABA1B1 körök képei a B'C'B1'C1', a C'A'C1'A1' és az A'B'A1'B1' körvonalak.
A Γ gömb definíciója szerint a Π sík és a Γ gömb merőlegesen metszi egymást a k kör mentén. Mivel az inverzió szögtartó, az Γ' sík és a Π' gömb is merőlegesen metszi egymást a k' kör mentén, így k' a Π' gömbnek főköre.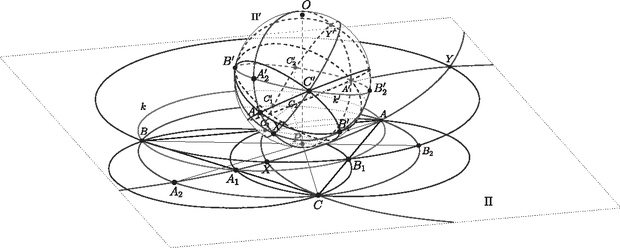

 
 

Vegyük észre, hogy az A' és A2' pontokon a Π' gömbnek legalább két különböző főköre is átmegy: ilyen a k' kör, és az OA'PA2' kör is. (Utóbbi átmegy az átellenes O és P pontokon, de nem szerepel az ábrán.) Ebből következik, hogy a Π' gömbön A' és A2' átellenes pontok, és az A'A1'A2' körvonal is főkör. Ez a főkör átmegy a C'A'C1'A1' és az A'B'A1'B1' körök metszéspontjain, A'-n és A1'-n; tehát az A'A1'A2 körvonal nem más, mint a C'A'C1'A1' és az A'B'A1'B1' körök hatványvonala.
Hasonlóan kapjuk, hogy a B'C'B1'C1' és az A'B'A1'B1' kör hatványvonala a B'B1'B2' főkör, illetve hogy a B'C'B1'C1' és az C'A'C1'A1' kör hatványvonala a C'C1'C2' főkör.
A három hatványvonal két, egymással átellenes közös ponton megy át; jelölje ezeket X' és Y' úgy, hogy X és O a k' főkör ellentétes oldalán legyenek. Az X', Y' pontokat O-ból visszavetítve a Π síkra, megkapjuk az AA1A2, BB1B2, és CC1C2 körök közös pontjait: az X pont a k körön belül, az Y pont a k körön kívül lesz.

 
3. Legyen K egy zárt konvex sokszöglemez, X pedig egy pont K síkjában. Mutassuk meg, hogy X a K sokszöglemez belsejébe vagy kerületére vihető a K bizonyos oldalegyeneseire alkalmas sorrendben végzett véges sok tengelyes tükrözés egymásutánjával, ha ugyanarra az oldalegyenesre többször is tükrözhetünk.
 
Megoldás. Alkossák a H halmazt a K sokszöglemez S síkjának mindazon pontjai, amelyek véges sok, a K oldalegyeneseire végzett tükrözés egymásutánjával K-ba vihetők. A mi feladatunk a H=S egyenlőség igazolása. Világos, hogy K⊆H, továbbá a konstrukció folytán H tükrös K minden oldalegyenesére. Legyen E a H tükörtengelyeinek halmaza. Világos, hogy ha t1,t2∈E és t1' a t1 tükörképe t2-re, akkor t1'∈E, ahol azaz H tükrös minden olyan egyenesre is, amelyet H egy tükörtengelyének a H egy másik tükörtengelyére való tükrözésével kapunk.
Mivel K⊆H, ezért H tükörszimmetriái folytán K-nak minden olyan K' képe is H-ban fekszik, amit K-ból E-beli egyenesekre vonatkozó tükrözések egymásutánjával kapunk. Ráadásul az így kapható K' sokszögek minden oldalegyenese E-beli, azaz a H egy tükörtengelye.
Jelölje r≥0 esetén Kr az S sík azon pontjait, amelyek legfeljebb r távolságra vannak a K sokszöglemeztől. Megmutatjuk, hogy Kr⊆H teljesül alkalmas r>0 esetén. Válasszunk egy olyan R>0 számot, amelyre a K csúcsai köré írt R sugarú körlemezek mindegyikének a K-val vett metszete körcikk. Egy ilyen R sugarú körcikk tükörképe a körcikket határoló sugár egyenesére H-ban fekszik, hiszen a tükrözés tengelyére H szimmetrikus. Sőt: ha a tükörképként kapott körcikket tükrözzük egy azt határoló sugár egyenesére, akkor az így kapott kép is H-ban marad, és ugyanez az így kapott tükörképek tükörképeire is igaz. Ezért a K csúcsai köré írt R sugarú körlemezek mindegyike része H-nak. Tekintsük a K sokszöglemeznek, a K csúcsai köré írt R sugarú köröknek és a K-nak a K oldalegyeneseire vett tükörképeinek K* unióját. Könnyen látható, hogy van olyan r>0 szám, amelyre Kr⊆K* teljesül, tehát alkalmas n-re
Kr⊆K1∪K2∪...∪Kn⊆H,(1)
ahol minden egyes Ki-t a H bizonyos tükörtengelyeire való tükrözések egymásutánjával kapunk K-ból.
Most tegyük fel, hogy Kt⊆H valamely t>0-ra. Vegyük észre, hogy ha azokat a tükrözéseket, amelyek a K sokszöget Ki-be viszik a K helyett a Kt alakzatra végezzük el, akkor a kapott kép éppen Kit lesz. Vagyis ha Kt⊆H, akkor Kit⊆H, amiből (1) miatt
K(r+t)⊆K1t∪K2t∪...∪Knt⊆H

következik. Az adódott tehát, hogy ha Kt⊆H, akkor Kt+r⊆H. Láttuk azonban, hogy Kr⊆H, ezért K2r⊆H, innen K3r⊆H stb. Így aztán
H⊆S=Kr∪K2r∪K3r∪...⊆H
adódik, ahonnan H=S következik, és nekünk pontosan ezt kellett igazolnunk.  □
 
Megjegyzések. 1. Úgy kaphatunk egy lehetséges másik megoldást a feladatra, ha követjük a fenti bizonyítás első két bekezdését, majd azt igazoljuk, hogy az S sík lefedhető azokkal a K-val egybevágó sokszöglemezekkel, amelyeket K-ból megkaphatunk annak az operációnak a véges sokszori alkalmazásával, amelyben egy sokszöglemezt tükrözünk annak egy oldalegyenesére. Minden így kapott K' sokszöglemez ugyanis része H-nak, hiszen H szimmetrikus az operáció során használt tükörtengelyekre. Érdemes megfigyelni az alábbiakat. Legyen P a K sokszöglemez S síkjának egy pontja. Kössük össze P-t a K egy Q belső pontjával, és indítsunk el egy biliárdgolyót Q-ból a QP félegyenes mentén. Ha a K sokszöglemezt egy biliárdasztalnak gondoljuk, amelynek határát elérve a bilárdgolyó a fizikai törvényeknek megfelelően pattan vissza (azaz úgy, hogy a visszapattanó golyó pályáját tükrözve az éppen elért oldal egyenesére pontosan az adott oldal elérését megelőző pályaegyenes meghosszabbítását kapjuk), akkor a K sokszöglemeznek az a pontja, amelybe a biliárdgolyó |PQ¯| távolság megtétele után kerül, egy olyan pont lesz, amelybe P betükrözhető. Ha a feladat megoldását erre a megfigyelésre szeretnénk alapozni, akkor vizsgálni kell, mi is történik akkor, ha a biliárdgolyó az útja során K egy csúcsába jut. Nem lehetetlen ezt az esetet jól kezelni, de azt sem nehéz igazolni, hogy ilyenkor Q helyett választható K-nak egy másik Q' pontja, amelyből a golyót útjára indítva már nem ütközünk K csúcsába. Egy másik nehézség annak igazolása, hogy bármelyik pontból bármelyik irányba is indítjuk a biliárdgolyót, az tetszőlegesen nagy távolságot meg tud tenni a K sokszöglemezen. Ennek belátását az olvasóra bízzuk.
2. Könnyen látható, hogy a feladatban nem lényeges feltétel a K sokszöglemez konvex volta. Tekintsük ugyanis K összes oldalegyenesét. Ezek a síkot konvex tartományokra bontják fel. A konstrukcióból adódóan minden ilyen tartomány vagy része K-nak vagy diszjunkt K belsejétől. Tekintsünk egy K-ban elhelyezkedő, konvex K' tartományt. A K' minden oldalegyenese egyúttal oldalegyenese K-nak is, ezért ha a K'-re igazoltuk a feladat állítását, akkor abból azonnal következik, hogy K is rendelkezik a kívánt tulajdonsággal. Sőt, az is igaz, hogy K oldalegyeneseire végrehajtott tükrözések egymásutánjával K síkjának tetszőleges pontja a K-nál szűkebb K' konvex sokszöglemez belsejébe vagy határára tükrözhető.