Kezdőlap


Cím:	Hengerlencsék képalkotása és a Fermat-elv
Szerző(k):	Gnädig Péter
Füzet:	2016/május, 296 - 304. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek, Egyéb lencsék

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A 2016. évi Nemzetközi Fizikai Diákolimpiára készülő diákok budapesti válogatóversenyének egyik érdekes optika feladata¹ így szólt:

Van két egyforma, vékony hengerlencsénk (egyik oldaluk sík, a másik egy

R

sugarú hengerpalást egy darabja, a törésmutatója

n

(1. ábra). A lencséket egy optikai padon helyezzük el úgy, hogy egymásra merőleges legyen a tengelyük. A leképező rendszer egyik oldalán van egy megvilágított családi fotó, attól

L

távolságra pedig egy ernyő, amin éppen éles képet látunk.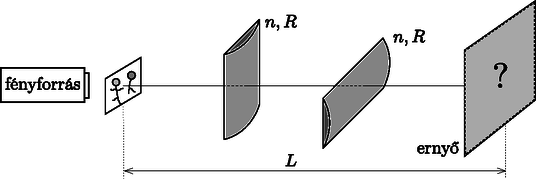

1. ábra

a)

Hova kell ehhez elhelyezni a lencséket az optikai padon?

b)

Hogyan néz ki a kép?

c)

Mi történik, ha felcseréljük a két lencsét?

Egy rávezető feladat és a probléma intuitív megoldása

Oldjunk meg először egy ‐ sokak által jól ismert ‐ könnyebb feladatot!
Helyezzünk el egy

n

törésmutatójú üvegből készült,

R

sugarú gömbfelület egy darabjával és egy síkfelülettel határolt (

f = R / (n - 1)

fókusztávolságú) vékony lencsét a családi fénykép és az attól

L

távolságban lévő ernyő közé! Hová tegyük ezt a sík-domború lencsét, ha az ernyőn éles képet szeretnénk kapni?
A leképezési törvény szerint

\begin{matrix} \frac{1}{t} + \frac{1}{L - t} = \frac{1}{f}, \end{matrix}

ahonnan a lencse és a fénykép (a tárgy) közötti távolságra

\begin{matrix} t^{2} - L t + L f = 0 \end{matrix}

másodfokú egyenlet adódik, amelynek a megoldásai:

\begin{matrix} t_{1,2} = \frac{L \pm \sqrt[]{L (L - 4 f)}}{2} . \end{matrix}

Látható, hogy a feladatnak csak akkor van valós megoldása, ha

L \geq 4 f

, és ha

L

határozottan nagyobb, mint

4 f

, akkor két, egymástól

\begin{matrix} H = t_{1} - t_{2} = \sqrt[]{L (L - 4 f)} \end{matrix}

távolságban található megoldásunk is lesz.
Visszatérve az eredeti (a két hengerlencsés) problémához, azt sejthetjük, hogy a két lencse ,,egymástól függetlenül'' töri meg a fénysugarakat. A bal oldali hengerlencse vízszintes síkban úgy működik, mint egy gömbi lencse, függőlegesen pedig mint egy plánparalel lemez, a jobb oldali viszont éppen fordítva. Akkor lesz éles a kép, ha mindkét lencse (amelyek sem vízszintes, sem függőleges irányban nem ,,zavarják'' egymást) olyan helyen található, ahonnan éppen az ernyőre képezi le a tárgyat. Mivel (

L > 4 f

esetén) két ilyen hely van, ezért ez a ‐ váltott szereposztású ‐ leképezés megfelelően elhelyezett hengerlencsékkel ténylegesen megvalósítható. (A két vékony hengerlencsét keresztben, szorosan egymásra illesztve is elhelyezhetjük a két nevezetes hely bármelyikénél, és akkor ezek ott egyetlen ,,rendes'', gömbi lencseként viselkednek, jóllehet a képalkotásnál jelentős lencsehibák lépnek fel.)
A kép torzított lesz, mert a fényképhez közelebbi hengerlencse (vízszintes irányban) nagyít, a másik pedig (függőleges irányban) kicsinyít. Ha felcseréljük a hengerlencséket, szintén éles képet kapunk, de másképp torzul el a kép: felcserélődik a nyújtás és az összenyomás iránya.
Ez a (két hengerlencsés) feladat nem szokványos geometriájú, hiszen a leképezés csak két, egymásra merőleges síkban emlékeztet a szokásos sík-domború lencsékre. Ezekből az oldal- és felülnézeti vetületekből ,,raktuk össze'' ‐ intuitív módon ‐ a ferdén haladó sugarakhoz tartozó általános esetet. Megnyugtató lenne, ha a kapott ‐ egyébként helyes ‐ eredményt más, független gondolatmenettel is meg tudnánk erősíteni.

A Fermat-elv és a képalkotás

A Fermat-elv² szerint a fénysugarak olyan útvonalon jutnak el a tárgy valamely pontjából a kép megfelelő pontjába, amelyekre az ún. optikai úthossz (a törésmutatóval szorzott tényleges úthosszdarabok összege) a hozzá közeli útvonalakhoz képest minimális. Később ‐ hullámoptikai megfontolások, a Huygens‐Fresnel-elv³ alapján ‐ finomították az állítást. Kiderült, hogy nem a minimum az igazán lényeges feltétel (és az gyakran nem is teljesül), hanem az, hogy az egymáshoz közeli pályákon haladó fény terjedési ideje (ez a mennyiség az optikai úthosszal arányos) ,,első közelítésben'' ugyanakkora legyen, vagyis ez az idő a pályák eltérésére jellemző kis mennyiségnek csak 1-nél magasabb hatványa szerint változzék meg. (Az ilyen, első közelítésben változatlan kifejezéseket stacionáriusnak nevezik. A lokális minimum helyénél a ,,simán változó'' (differenciálható) függvény stacionárius, de ez fordítva nem igaz.)
A Huygens‐Fresnel-elv szerint a stacionárius pálya közelében lévő, de attól különböző pályákat is ,,kipróbáló'' fényhullámok jó közelítéssel azonos idő alatt, tehát azonos fázisban érkeznek meg a ,,célba'', emiatt interferenciával felerősítik egymást.
A képalkotáshoz a fentieknél több is szükséges: ha nem csak egyetlen egy, hanem sok-sok különböző (önmagában mind stacionárius) úton is eljuthat a fény a tárgy pontjaiból a kép pontjaiba, akkor ott intenzitásmaximumot, tehát fényes pontot észlelünk. Ha az egymástól nem túl messzi, de a fény hullámhosszánál lényegesen nagyobb távolságra haladó fénysugarak mindegyikének optikai úthossza stacionárius, akkor ezek egymással is megegyező értékűek kell hogy legyenek.
Ez az optikai törvény (amely egységes leírását adja a fény visszaverődésének és törésének) elvi érdekessége és ,,szépsége'' mellett konkrét számolásokra is alkalmas és célravezető lehet, még olyan bonyolultnak látszó esetekben is, mint a hengerlencsék képalkotása.

Közelítő számítások

A számolás során fel fogjuk használni a következő közelítő képleteket:

I. Ha

ε ≪ a

, akkor

\begin{matrix} \sqrt[]{a^{2} + ε^{2}} \approx a + \frac{ε^{2}}{2 a} . \end{matrix}

(*)

A közelítés

ε^{2}

pontosságú, vagyis akkor ,,válik'' egyenlőséggé, ha

ε

kettőnél nagyobb kitevőjű hatványait elhanyagolhatóan kicsinek tekinthetjük.
Az állítás belátásához emeljük négyzetre a jobb oldalon álló kifejezést:

\begin{matrix} {(a + \frac{ε^{2}}{2 a})}^{2} = a^{2} + 2 a \cdot \frac{ε^{2}}{2 a} + \frac{ε^{4}}{4 a^{2}} \approx a^{2} + ε^{2} . \end{matrix}

II. Tekintsünk egy

R

sugarú gömböt és egy síkot, amely az

A

pontban érinti a gömböt, valamint a gömb egy olyan

P

pontját, amely az

A

ponthoz tartozó

A O

sugártól

r ≪ R

távolságra van (2. ábra).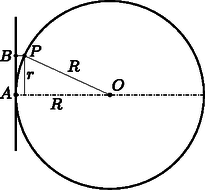

2. ábra

Ekkor a

P

pont és az érintősík távolsága:

\begin{matrix} B P = R - \sqrt[]{R^{2} - r^{2}} \approx \frac{r^{2}}{2 R}, \end{matrix}

(**)

amit a (*) összefüggés alkalmazásával, vagy az alábbi algebrai átalakítás segítségével láthatunk be:

\begin{matrix} R - \sqrt[]{R^{2} - r^{2}} = \frac{(R - \sqrt[]{R^{2} - r^{2}}) (R + \sqrt[]{R^{2} - r^{2}})}{R + \sqrt[]{R^{2} - r^{2}}} = \frac{r^{2}}{R + \sqrt[]{R^{2} - r^{2}}} \approx \frac{r^{2}}{2 R} . \end{matrix}

Gyűjtőlencse képalkotása

A Fermat-elv alkalmazására először tekintsünk egy egyszerűbb esetet, az

R_{1}

és

R_{2}

görbületi sugarú gömbfelületekkel határolt,

d

vastagságú (gömbi) gyűjtőlencse képalkotását. Helyezzünk el egy

T

nagyságú tárgyat a lencsétől

t

távolságra, és vizsgáljuk meg, hogy milyen feltételek mellett kapunk leképezést a lencsétől

k

, az optikai tengelytől

K

távolságban (3. ábra). Feltételezzük, hogy

d

r

T

és

K

mindegyike sokkal kisebbek, mint

t

k

R_{1}

és

R_{2}

, vagyis a lencse ,,vékony'', és a képalkotásban csak az optikai tengelyhez közel haladó fénysugarak vesznek részt.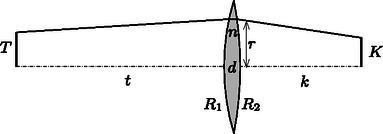

3. ábra

Megjegyzés. Jól ismert, hogy a gyüjtőlencse által létrehozott valódi kép ‐ az ábrán jelölt helyzettel ellentétben ‐ fordított állású. Várjuk, hogy ez

K < 0

formában ,,kijöjjön'' a Fermat-elvre alapozott számításból.

A 3. ábrán látható fénysugárra az optikai úthossz a (**) közelítés alkalmazásával

\begin{matrix} s = \sqrt[]{t^{2} + {(T - r)}^{2}} + \frac{r^{2}}{2 R_{1}} + n (d - \frac{r^{2}}{2 R_{1}} - \frac{r^{2}}{2 R_{2}}) + \frac{r^{2}}{2 R_{2}} + \sqrt[]{k^{2} + {(K - r)}^{2}}, \end{matrix}

ami (*) felhasználásával így írható:

\begin{matrix} s \approx (t + \frac{T^{2}}{2 t} + k + \frac{K^{2}}{2 k} + n d) - (\frac{T}{t} + \frac{K}{k}) r + [\frac{1}{t} + \frac{1}{k} - (n - 1) (\frac{1}{R_{1}} + \frac{1}{R_{2}})] \frac{r^{2}}{2} . \end{matrix}

Ez a kifejezés (az adott közelítésben) akkor lesz

r

-től független állandó, vagyis stacionárius, ha

r

és

r^{2}

együtthatója külön-külön nulla, vagyis fennáll

\begin{matrix} \frac{K}{T} = - \frac{k}{t}, \end{matrix}

(1)

illetve

\begin{matrix} \frac{1}{t} + \frac{1}{k} = (n - 1) (\frac{1}{R_{1}} + \frac{1}{R_{2}}) . \end{matrix}

(2)

Megkaptuk tehát, hogy a kép fordított állású, és a nagyítás

\begin{matrix} N = \frac{| K |}{T} = \frac{k}{t} . \end{matrix}

Azt is látjuk, hogy ha a (2) jobb oldalán szereplő (csak a lencse adataitól függő) kifejezést a szokásos módon

1 / f

-fel jelöljük, teljesül az ismert lencsetörvény:

\begin{matrix} \frac{1}{t} + \frac{1}{k} = \frac{1}{f} . \end{matrix}

(,,Melléktermékként'' az is kiderült, hogy mi a kapcsolat a lencse anyagának törésmutatója, a görbületi sugarak és az

f

fókusztávolság között.)

Két hengerlencse képalkotása

Térjünk most rá az eredeti probléma, a két ‐ egymásra merőlegesen elhelyezett ‐ hengerlencse képalkotására. Mivel most a leképező rendszer nem forgásszimmetrikus, nem elegendő a tárgy- és képpontoknak az optikai tengelytől mért

T

és

K

távolságát megadnunk, hanem egy-egy kétdimenziós vektorral (vagyis 4 adattal) kell jellemezzük azokat (4. ábra).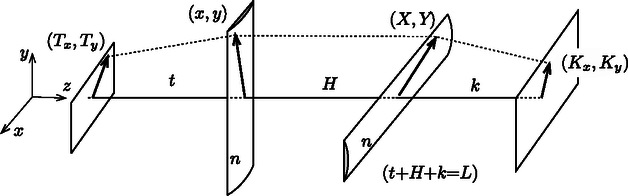

4. ábra

Vizsgáljuk meg, hogy a tárgytól és az ernyőtől mekkora

t

, illetve

k

távolságra kell elhelyeznünk a hengerlencséket, hogy a

(T_{x}, T_{y})

tárgyvektorról (a családi fénykép egyik pontjáról) a

(K_{x}, K_{y})

képvektor helyén keletkezzen éles kép.
Ha a lencsék vastagsága

d

, és a fény az

(x, y)

, illetve az

(X, Y)

koordinátájú pontokban éri el az egyik, illetve másik hengerlencsét, akkor az optikai úthossz így írható fel:

\begin{matrix} s & = \sqrt[]{t^{2} + {(T_{x} - x)}^{2} + {(T_{y} - y)}^{2}} + n (d - \frac{x^{2}}{2 R}) + \frac{x^{2}}{2 R} + & (4) \\ + \sqrt[]{H^{2} + {(x - X)}^{2} + {(y - Y)}^{2}} + n (d - \frac{Y^{2}}{2 R}) + \frac{Y^{2}}{2 R} + \\ + \sqrt[]{k^{2} + {(X - K_{x})}^{2} + {(Y - K_{y})}^{2}} . \end{matrix}

(A lencsék vékonysága miatt az üvegben haladó fény útját az optikai tengellyel párhuzamosnak tekintettük, az ettől való eltérés ugyanis a figyelembe vett pontosság mellett elhanyagolható.) A (4) kifejezés a (*) közelítés felhasználásával ilyen alakba írható:

\begin{matrix} s (x, y, X, Y) = (t + k + H + 2 d n) + \frac{{(T_{x} - x)}^{2}}{2 t} + \frac{{(T_{y} - y)}^{2}}{2 t} + (1 - n) \frac{x^{2}}{2 R} + & (5) \\ + \frac{{(x - X)}^{2}}{2 H} + \frac{{(y - Y)}^{2}}{2 H} + (1 - n) \frac{Y^{2}}{2 R} + \frac{{(K_{x} - X)}^{2}}{2 k} + \frac{{(K_{y} - Y)}^{2}}{2 k} . \end{matrix}

A Fermat-elv (annak Huygens-Fresnel-féle általánosítása) szerint az optikai úthossz bármelyik változója, tehát például

y

szerint is stacionáriusnak kell lennie. Mivel

y

csak két tagban, és azokban is legfeljebb második hatványon fordul elő, teljes négyzetté alakítással (vagy deriválással) könnyen megkaphatjuk a stacionárius pont (ami itt most éppen minimum) helyét:

\begin{matrix} f (y) \equiv \frac{{(T_{y} - y)}^{2}}{2 t} + \frac{{(y - Y)}^{2}}{2 H} = \frac{1}{2} (\frac{1}{t} + \frac{1}{H}) {(y - y_{0})}^{2} + f_{min}, \end{matrix}

(6)

ahol a minimum helye:

\begin{matrix} y_{0} = \frac{H}{t + H} T_{y} + \frac{t}{t + H} Y, \end{matrix}

értéke pedig

\begin{matrix} f_{min} = \frac{{(Y - T_{y})}^{2}}{2 (t + H)} . \end{matrix}

(7)

A minimum helyénél teljesül, hogy

\begin{matrix} \frac{T_{y} - y_{0}}{t} = \frac{y_{0} - Y}{H} . \end{matrix}

Megjegyzés. Az itt kiszámított minimumhelynek egyszerű, szemléletes jelentése van: a fénysugár ,,vízszintes nézete'' törésmentesen halad át a függőlegesen álló hengerlencsén, éppen úgy, mint egy elhanyagolható vastagságú plánparalel lemezen (5. ábra). Ezen út mentén az optikai úthossz (ami most a tényleges úthosszal egyezik meg) adott

A

és

B

pontok mellett azon

P

pontnál minimális, amely az

A B

egyenesre illeszkedik. A minimum értéke a (*) közelítést alkalmazva:

\begin{matrix} A P + P B = A B \approx t + H + \frac{{(Y - T_{y})}^{2}}{2 (t + H)} . \end{matrix}

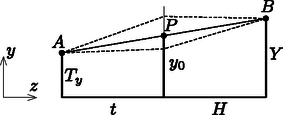5. ábra

Hasonló módon kapjuk az

X

-et tartalmazó tagok minimumát:

\begin{matrix} g (X) \equiv \frac{{(x - X)}^{2}}{2 H} + \frac{{(K_{x} - X)}^{2}}{2 k} \geq g_{min} = \frac{{(x - K_{x})}^{2}}{2 (k + H)}, \end{matrix}

(8)

és a szélsőértéknek megfelelő

\begin{matrix} X_{0} = \frac{H}{H + k} K_{x} + \frac{k}{H + k} x \end{matrix}

esetben a fénysugár ,,függőleges nézete'' törésmentesen halad át a vízszintesen elhelyezkedő (jobb oldali) hengerlencsén.
Írjuk be az optikai úthossz (5) kifejezésébe a (7) és (8) összefüggéseknek megfelelő minimális értékeket. Ekkor az optikai úthossz már csak 2 változótól,

x

-től és

Y

-tól fog függeni, jóllehet még számos ‐ rögzítettnek gondolt ‐ kifejezést (,,paramétert'') is tartalmaz:

\begin{matrix} s (x, Y) & = s (x, y_{0}, X_{0}, Y) = s_{0} + \frac{{(T_{x} - x)}^{2}}{2 t} + (1 - n) \frac{x^{2}}{2 R} + & (9) \\ + \frac{{(Y - T_{y})}^{2}}{2 (t + H)} + (1 - n) \frac{Y^{2}}{2 R} + \frac{{(K_{y} - Y)}^{2}}{2 k} + \frac{{(K_{x} - x)}^{2}}{2 (H + k)} . \end{matrix}

Az optikai úthossz stacionaritásának feltétele szerint a fenti kifejezés ‐ az alkalmazott közelítések mellett ‐ sem

x

-től, sem

Y

-tól nem szabad függenie. Ez a követelmény egy sor megszorítást ad a paraméterek között.
Az

x

-ben és

Y

-ban lineáris tag együtthatójának eltűnéséből

\begin{matrix} \frac{T_{x}}{t} + \frac{K_{x}}{H + k} = 0, illetve \frac{T_{y}}{t + H} + \frac{K_{y}}{k} = 0, \end{matrix}

vagyis a vízszintes és függőleges irányú nagyítások:

\begin{matrix} N_{x} = | \frac{K_{x}}{T_{x}} | = \frac{H + k}{t}, \end{matrix}

(10)

illetve

\begin{matrix} N_{y} = | \frac{K_{y}}{T_{y}} | = \frac{k}{H + t} . \end{matrix}

(11)

A kép lényegében fordított állású, jóllehet (

N_{x} \neq N_{y}

miatt) a

(T_{x}, T_{y})

és a

(K_{x}, K_{y})

vektor nem pontosan ellentétes irányú.
A négyzetes tagok együtthatói is nullák (hiszen a különböző fénysugarak optikai úthossza stacionáris, tehát azok egymással is megegyezőek):

\begin{matrix} \frac{1}{t} + \frac{1}{H + k} = \frac{1}{f} \end{matrix}

(12)

és

\begin{matrix} \frac{1}{t + H} + \frac{1}{k} = \frac{1}{f}, \end{matrix}

(13)

ahol

f = R / (n - 1)

. A (12) és (13) egyenletekből

t + k + H = L

felhasználásával

\begin{matrix} H = \sqrt[]{L (L - 4 f)} és t = k = \frac{L - H}{2} \end{matrix}

következik. Ezt (10) és (11)-be helyettesítve megkapjuk a különböző irányú nagyításokat:

\begin{matrix} N_{x} = 1 + \frac{H}{t} \geq 1, N_{y} = \frac{1}{N_{x}} \leq 1. \end{matrix}

Ha a két hengerlencsét felcseréljük, éppen olyan elrendezést kapunk, mintha az optikai tengely körül

90^{\circ}

-kal elforgattuk volna a lencséket. Ekkor (változatlan

t

és

k

mellett) ismét éles képet kapunk az ernyőn, de a nagyítások felcserélődnek: a leképező rendszer

x

irányban (vízszintesen) fog kicsinyíteni,

y

irányban (függőlegesen) pedig nagyítani.
Az eredmény ‐ mind a lencsék elhelyezkedése, mind pedig a nagyítások tekintetében ‐ megegyezik az intuitív megoldásban kapottakkal.

Megjegyzés. Az Olvasóban felmerülhet a kérdés, vajon nem jártunk-e el következetlenül, amikor az optikai úthossz (5) képletét, annak stacionaritását vizsgáltuk. Kiválasztottunk

s (x, y, X, Y)

négy változója közül kettőt (

y

-t és

X

-et), és ezen változók szerint minimumot kerestünk, majd a minimum értékeket visszahelyettesítettük

s

-be. Az így kapott (a maradék két változótól függő, a (9) összefüggéssel megadott)

s (x, Y)

-tól megköveteltük, hogy ‐ másodrendig bezárólag ‐ egyik változójától se függjön, vagyis

x

x^{2}

Y

és

Y^{2}

együtthatója mind nulla legyen. Miért nem voltunk ilyen ,,szigorúak'' az (5) kifejezéssel, miért nem mondtuk, hogy a képalkotáshoz (5) minden változójától független legyen?
Ha (5)-ben (vagy az ezzel egyenértékű (6) kifejezésben) megkövetelnénk, hogy

y^{2}

együtthatója nulla legyen, akkor a teljesíthetetlen

\begin{matrix} \frac{1}{t} + \frac{1}{H} = 0 \end{matrix}

feltételhez jutnánk. Ez azt mutatja, hogy

y

(a többi változó és paraméter adott értéke mellett) nem lehet akármekkora, vagyis a képalkotásban nem minden

y

-nak megfelelő fénysugár vesz részt. Ott, ahol

y = y_{0}

, a (6) kifejezés (

y

kicsiny változásaira nézve) stacionárius, de az egész

f (y)

‐ másodrendig bezáróan ‐ nem állandó. Fizikailag ez annak felel meg, hogy a fény (adott

T_{y}

és

Y

mellett) csak olyan pályán haladhat, amelynek

y - z

síkra eső vetülete megtörés nélküli egyenes, ahogy azt az 5. ábra mutatja. Ugyanez a helyzet az

X

változóval is a (8) kifejezésben, ott is csak a minimumot követelhetjük meg, nem pedig a

g (X)

függvény állandóságát.
Más a helyzet a maradék 2 változóval,

x

-szel és

Y

-nal. Ha a paramétereket megfelelően választjuk, akkor elérhetjük, hogy a (9)-ben szereplő kifejezés sem

x

-től, sem

Y

-tól ne függjön, vagyis a képalkotásban minden (az optikai tengelyhez közeli) fénysugár részt vegyen. Természetesen a kiszemelt változók kiválasztása önkényes: megtehettük volna azt is, hogy

x

-ben és

Y

-ban követelünk meg szélsőértéket, majd ezeket visszahelyettesítve

s

-be a maradék két változó, vagyis

y

és

X

első és második hatványának eltűnését írjuk elő.

¹Werner Miklós Antal (BME Fizikai Intézet) feladata.

²Pierre de Fermat (1601‐1665) francia jogász, korának műkedvelő matematikusa.

³Christiaan Huygens (1629‐1695) holland matematikus, fizikus és csillagász; Augustin-Jean Fresnel (1788‐1827) francia fizikus, legfontosabb eredményeit az optika területén érte el.