Kezdőlap


Cím:	Megoldásvázlatok a 2010/6. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Gerőcs László
Füzet:	2010/október, 404 - 411. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. rész

1. Juli néni két területen termesztett burgonyát, amelyek közül az egyik kétszer akkora volt, mint a másik. A burgonya betakarításához segítségül hívta rokonait, barátait. Az első napon az egész csapat a nagyobb területen dolgozott. A második napon a csapat fele átment a kisebb területre, a csapat másik fele tovább végezte a munkát a nagyobb területen, és így ezt a második nap végére be is fejezték. A kisebb területen nem végeztek, így a harmadik napon

12

embernek kellett dolgoznia ahhoz, hogy itt is befejezzék a betakarítást. Tudjuk, hogy mindhárom napon ugyanannyi ideig dolgoztak, és az emberek teljesítményét egyenlőnek vehetjük. Hány fős csapat dolgozott a betakarításnál? (11 pont)

Megoldás. Legyen a csapat

n

fős, és legyen

e

egy ember napi munkamennyisége. A nagyobb földterület betakarításához szükséges munka mennyisége:

(n + \frac{n}{2}) \cdot e

, a kisebbhez szükséges pedig:

(\frac{n}{2} + 12) \cdot e

.
Mivel a kisebb parcella területe a nagyobb parcella területének a fele, azért

\begin{matrix} 2 \cdot (\frac{n}{2} + 12) \cdot e = (n + \frac{n}{2}) \cdot e, azaz n + 24 = \frac{3}{2} n . \end{matrix}

Innen

n = 48

.
Tehát a betakarítást 48 fő végezte.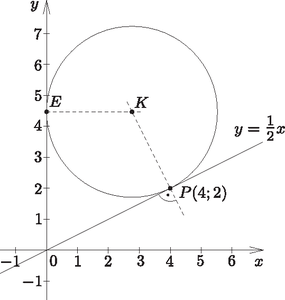

2. Írjuk fel annak a körnek az egyenletét, amelyik a

P (4; 2)

pontban érinti az

y = \frac{1}{2} x

egyenest, valamint érinti az

y

tengelyt. (13 pont)

Megoldás. Készítsük el a szükséges 1. ábrát. Ha a keresett kör a megadott egyenest a

P

pontban érinti, akkor a

K

középpontja rajta van az egyenesre

P

-ben állított merőleges egyenesen.

1. ábra

A megadott egyenes meredeksége:

m = \frac{1}{2}

, így a rá merőleges egyenesek meredeksége:

m^{*} = - 2

. Ezzel a

P K

egyenes egyenlete:

y - 2 = - 2 \cdot (x - 4)

, azaz

y = - 2 x + 10

. Ezek szerint, ha a

K

középpont első koordinátája

x_{0}

, akkor

K (x_{0}; - 2 x_{0} + 10)

.
A feltételek szerint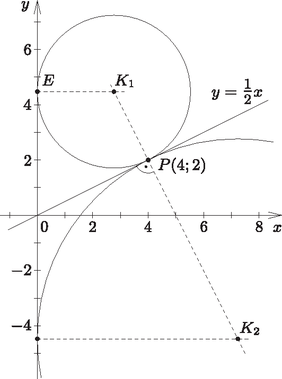

K E = K P

, azaz

\begin{matrix} x_{0} & = \sqrt[]{{(x_{0} - 4)}^{2} + {(- 2 x_{0} + 8)}^{2}}, \\ x_{0}^{2} & = x_{0}^{2} - 8 x_{0} + 16 + 4 x_{0}^{2} - 32 x_{0} + 64, \\ x_{0}^{2} & - 10 x_{0} + 20 = 0, \\ {(x_{0})}_{1,2} & = \frac{10 \pm \sqrt[]{100 - 80}}{2} = \frac{10 \pm \sqrt[]{20}}{2} = 5 \pm \sqrt[]{5} . \end{matrix}

A feladatnak két megoldása van, amit a 2. ábra szemléltet.

2. ábra

A körközéppontok:

K_{1} (5 - \sqrt[]{5}; 2 \sqrt[]{5})

K_{2} (5 + \sqrt[]{5}; - 2 \sqrt[]{5})

. A feltételeknek eleget tevő körök egyenletei:

\begin{matrix} {(x - (5 - \sqrt[]{5}))}^{2} + {(y - 2 \sqrt[]{5})}^{2} = {(5 - \sqrt[]{5})}^{2}, \\ {(x - (5 + \sqrt[]{5}))}^{2} + {(y + 2 \sqrt[]{5})}^{2} = {(5 + \sqrt[]{5})}^{2} . \end{matrix}

a)

Egy 12 cm belső sugarú, egyenes henger alakú fazékban 18 cm magasan áll a leves. Ezt a levest egy téglatest alakú műanyag edénybe szeretnénk önteni és hűtőszekrénybe helyezni. Az edény belső élei 26 cm, 22 cm és 16 cm hosszúak. Belefér-e a leves ebbe az edénybe? (5 pont)

b)

Egy 10 cm sugarú, 8 cm magas egyenes henger alakú gyertyát felolvasztunk, és olyan kisebb, 6 cm-es sugarú, egyenes henger alakú gyertyákat szeretnénk önteni belőle, melyek felszínének mérőszáma egyenlő térfogatuk mérőszámával. Hány darab kis gyertyát tudunk így készíteni? (8 pont)

Megoldás.

a)

A leves térfogata:

12^{2} \cdot π \cdot 18 \approx 8143 {cm}^{3}

. A műanyag edény térfogata:

26 \cdot 22 \cdot 16 = 9152 {cm}^{3}

. Tehát a leves belefér a műanyag edénybe.

b)

Az eredeti nagy gyertya térfogata:

V_{1} = 10^{2} \cdot π \cdot 8 \approx 2513, 3 {cm}^{3}

. Ha a kiöntendő kis gyertyák sugara 6 cm, magasságuk

m

, és felszínük mérőszáma egyenlő térfogatuk mérőszámával, akkor

\begin{matrix} 6^{2} \cdot π \cdot m = 2 \cdot π \cdot 6 \cdot (m + 6), azaz 6 m = 2 m + 12, \end{matrix}

ahonnan

m = 3

.
A kiöntendő kis gyertyák térfogata:

V_{2} = 6^{2} \cdot π \cdot 3 \approx 339, 3

. A kiönthető kis gyertyák száma:

\begin{matrix} \frac{V_{1}}{V_{2}} \approx \frac{2513, 3}{339, 3} \approx 7, 4. \end{matrix}

Tehát a nagy gyertyából az adott feltételek mellett 7 db kis gyertyát lehet kiönteni.

4. Egy iskolák közötti csapatverseny döntőjébe

4

iskola jutott, iskolánként

3

fős csapattal. A verseny előtt a résztvevők felsorakoztak egy fotózáshoz.

a)

Hányféleképpen állhattak sorba a versenyzők, ha azt akarták, hogy az azonos iskolába járó diákok egymás mellett álljanak? (4 pont)

b)

12

résztvevő között

4

lány és

8

fiú volt. Hányféleképpen állhattak sorba a versenyzők a fotózáshoz, ha azt akarták, hogy a

4

lány középen álljon egymás mellett? (4 pont)

c)

Egy másik, iskolák közötti csapatversenyen

4

fős csapatok vettek részt (egy iskola csak egy csapattal nevezhetett). E verseny kezdetén a résztvevők bemutatkoztak egymásnak; minden diák minden olyan diákkal kezet fogott, aki nem iskolatársa, így összesen

336

kézfogásra került sor. A versenyt követő búcsúesten minden diák minden diákkal koccintott egy pohár üdítővel. Hány koccintásra került sor ekkor? (6 pont)

Megoldás.

a)

Először a 4 iskolát állítjuk sorrendbe. Ezt

4!

-féleképpen tehetjük meg.

Bárhogyan is állítottuk sorrendbe a 4 iskolát, az 1., a 2., a 3. és a 4. iskola három-három diákját

3!

-féleképpen állíthatjuk sorba. Ezek szerint a kívánt módon a 12 diákot

4! \cdot {(3!)}^{4} = 24 \cdot 6^{4} = 31 104

-féleképpen állíthatjuk sorba.

b)

A fiúkat összesen 8!-féleképpen állíthatjuk sorba. Bárhogyan is állítjuk sorba a 8 fiút, közéjük (középen) a 4 lányt

4!

-féleképpen helyezhetjük el.

Tehát a feltételeket figyelembe véve a 12 diákot összesen

8! \cdot 4! = 967 680

-féleképpen állíthatjuk sorba.

c)

Legyen a versenyen résztvevő iskolák száma

n

. Ekkor a résztvevő diákok száma

4 n

. Ha a versenyt megelőzően minden diák kézfogással bemutatkozott minden olyan diáknak, aki nem iskolatársa, akkor minden diák

4 n - 4

diákkal fogott kezet. Mivel a

4 n

diák mindegyike ennyi kézfogást tett, azért a verseny előtt a kézfogások száma:

\begin{matrix} \frac{4 n (4 n - 4)}{2} = 336, \\ 16 n^{2} - 16 n = 672, \\ n^{2} - n - 42 = 0, \\ n_{1,2} = \frac{1 \pm \sqrt[]{1 + 168}}{2} = \frac{1 \pm 13}{2}, \\ n_{1} = 7, n_{2} = - 6. \end{matrix}

A negatív gyök érdektelen számunkra, így azt kaptuk, hogy a résztvevő iskolák száma 7.
Ezek szerint a versenyen résztvevő diákok száma

7 \cdot 4 = 28

. Így a verseny végén ‐ amikor mindenki mindenkivel koccintott egyszer ‐ összesen

\frac{28 \cdot 27}{2} = 378

koccintás hallatszott.

II. rész

5. Egy ország öt nagyvárosában (

A

B

C

D

és

E

-ben) összesen

27

bevásárlóközpont működik.

A

-ban

7

B

-ben

3

C

-ben

3

D

-ben

6

és

E

-ben

8

. Közülük

12

-ben van mozi,

16

-ban van étterem, és

13

-ban van autómosó szolgáltatás.

3

olyan bevásárlóközpont van, ahol mindhárom szolgáltatást nyújtják.

a)

A mozival rendelkező bevásárlóközpontok közül

5

-ben nincs autómosó, az étteremmel rendelkezők közül pedig

5

-ben van mozi.

9

olyan bevásárlóközpont van, melyekben e szolgáltatások közül csak étterem van. Hány olyan bevásárlóközpont van az öt városban, melyben pontosan két szolgáltatást nyújtanak e három közül? (10 pont)

b)

Mutassuk meg, hogy ha a

27

bevásárlóközpont között

16

olyan van, amelyben csak egy szolgáltatást nyújtanak, akkor legalább

3

város rendelkezik olyan bevásárlóközponttal, melyben csak egy szolgáltatás van a fentiek közül. (6 pont)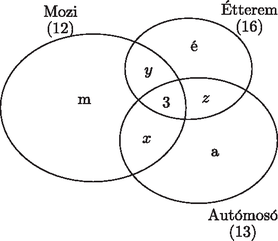

Megoldás.

a)

Készítsünk egy halmazábrát (1. ábra), melyben a mozik, éttermek és autómosók számát szemléltetjük. A három halmaz metszetének 3 eleme van.

1. ábra

Mivel a mozival rendelkező bevásárlóközpontok közül 5-ben nincs autómosó, azért

m + y = 5

, vagyis

x = 12 - (m + y + 3) = 4

. Az étteremmel rendelkezők közül 5-ben van mozi, tehát

y + 3 = 5

, azaz

y = 2

, és ekkor

m = 3

. 9 olyan bevásárlóközpont van, melyekben csak étterem van, vagyis

é = 9

. Ezzel pedig

z = 2

, és így

a = 4

.
Most már kitölthetjük a halmazábrát (2. ábra). A pontosan két szolgáltatással rendelkező bevásárlóközpontok száma: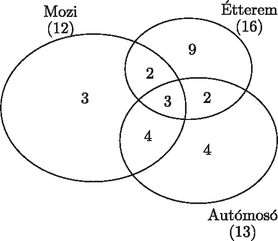

\begin{matrix} y + z + x = 2 + 2 + 4 = 8. \end{matrix}

2. ábra

b)

Ha a legtöbb bevásárlóközponttal rendelkező két város (

A

-ban 7,

E

-ben 8) mindegyikében minden bevásárlóközpontban csak egy szolgáltatást nyújtanának, akkor ez 15 bevásárlóközpont. Tudjuk, hogy a 27 bevásárlóközpont között összesen 16 olyan van, amelyben csak egy szolgáltatást nyújtanak. Ezek szerint mindenképpen kell még egy olyan városnak lennie, melyben van csak egy szolgáltatást nyújtó bevásárlóközpont.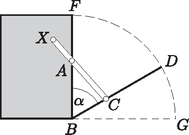

6. Egy szekrényhez erősített, lehajtható munkaasztalt látunk az ábrán. A

B D

lehajtható munkalapot az

X C

fémkar segítségével mozgathatjuk. Az

A

pontban levő szegecs a szekrény

B F

oldalába van erősítve, ezen a szegecsen csúszhat a fémkar. Tudjuk, hogy

B C = 36 cm

A B = 48 cm

. Felhajtott helyzetben a

D

és az

X

pontok egybeesnek az

F

ponttal. Lehajtott helyzetben a

D

és a

G

pontok, valamint az

X

és az

A

pontok is egybeesnek.

a)

Milyen hosszú az asztal

B D

oldala? (8 pont)

b)

Milyen távol lesz az

X

pont a szekrény

B F

oldalától, ha az asztallapot

B

körül

α = 60^{\circ}

-kal lehajtjuk? (8 pont)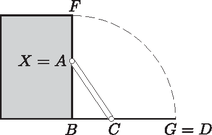

Megoldás.

a)

Képzeljük el a munkaasztalt lehajtott helyzetben (1. ábra). Ekkor a Pitagorasz-tétel alapján:

X B^{2} + B C^{2} = X C^{2}

, azaz

48^{2} + 36^{2} = X C^{2}

, ahonnan

X C = 60

cm. A munkaasztal

B G

oldalának hossza egyenlő az

F B

oldal hosszával. Felhajtott állapotban

\begin{matrix} B D = B G = B F = X C + C B = 60 + 36 = 96 cm. \end{matrix}

1. ábra

b)

Először számítsuk ki koszinusztétel segítségével az

A B C

háromszög

A C

oldalának hosszát, majd szinusztétellel a

B A C = β

szöget. Ezek birtokában már könnyen meghatározhatjuk a 2. ábra

X T A

derékszögű háromszögéből a keresett

X T = x

szakasz hosszát.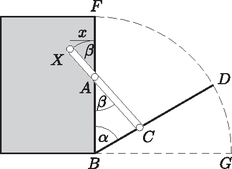

2. ábra

A B C

háromszögben

\begin{matrix} A C^{2} & = 48^{2} + 36^{2} - 2 \cdot 48 \cdot 36 \cdot cos 60^{\circ}, \\ A C^{2} & = 3600 - 1728 = 1872, ahonnan A C \approx 43, 3. \end{matrix}

Ugyancsak az

A B C

háromszögben:

\begin{matrix} \frac{sin β}{sin 60^{\circ}} = \frac{B C}{A C}, azaz sin β = \frac{sin 60^{\circ} \cdot 36}{43, 3} \approx 0, 7200. \end{matrix}

A X T

derékszögű háromszög

A X

oldala:

\begin{matrix} A X = X C - A C = 60 - 43, 3 \approx 16, 7. \end{matrix}

Ezzel

sin β = \frac{x}{A X}

, azaz

0, 7200 = \frac{x}{16, 7}

, ahonnan

x \approx 12

.
Tehát az

X

pont a szekrény

B F

oldalától ‐ az asztallap

60^{\circ}

-os lehajtása esetén ‐ kb. 12 cm távol lesz.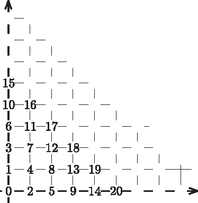

7. A derékszögű koordinátarendszer rácspontjaiba beírtuk a természetes számokat az ábrán látható módon. (A rácspont olyan pont, melynek mindkét koordinátája egész szám.)

a)

Milyen koordinátájú pontban van a 2010? (9 pont)

b)

Milyen szám szerepel a

P (54; 72)

koordinátájú pontban? (7 pont)

Megoldás.

a)

Tekintsük az

y

tengely egész koordinátájú pontjaiból kiinduló ,,ferde'' sorokat, melyekben egymást követik a természetes számok. Az egyes ilyen ferde sorokban levő számok rendre 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 stb. Észrevehetjük, hogy az

y

tengely

P (0; n)

pontjából induló sor első száma egyenlő az előtte levő sorokban levő számok számának összegével, azaz

\begin{matrix} 0 + 1 + 2 + 3 + 4 + ... + n = \frac{n (n + 1)}{2} . \end{matrix}

Így a

P (0; n + 1)

koordinátájú ponttal kezdődő sor első száma:

\begin{matrix} \frac{(n + 1) (n + 2)}{2} . \end{matrix}

Ezek szerint ha a 2010 szám abban a ferde sorban van, melynek első tagja az

y

tengely

P (0; n)

pontjában van, akkor

\begin{matrix} \frac{n (n + 1)}{2} \leq 2010 < \frac{(n + 1) (n + 2)}{2}, azaz n^{2} + n \leq 4020 < n^{2} + 3 n + 2. \end{matrix}

Az első egyenlőtlenségből

n \leq 62, 9

, a másodikból pedig

n > 61, 9

. Tehát a 2010 az

y

tengely

P (0; 62)

koordinátájú pontjából induló ferde sorban van, és az itt található szám:

\begin{matrix} \frac{62 \cdot 63}{2} = 1953. \end{matrix}

Mivel

2010 - 1953 = 57

, azért a

P (0; 62)

pontból kiindulva 57 lépést kell tennünk jobbra és lefelé, hogy eljussunk a 2010 számhoz.
Tehát a 2010 szám a koordinátarendszer

Q (57; 5)

koordinátájú pontjában van.

b)

P (54; 72)

koordinátájú pontból kiindulva, 54 lépést haladva ,,balra'', az

y

tengelyen a

(0; 72)

koordinátájú pontba jutunk. Innen újabb 54 lépést haladva ,,felfelé'' az

y

tengelyen eljutunk a

(0; 126)

koordinátájú pontba. Ebben a pontban az előzőek alapján a

\frac{126 \cdot 127}{2} = 8001

szám szerepel. Tehát a

P (54; 72)

koordinátájú pont abban a ferde sorban van, amely első pontjának koordinátái

(0; 126)

, a szám pedig a 8001. Innen 54-et lépve azt kapjuk, hogy a

P (54; 72)

koordinátájú pontban levő szám: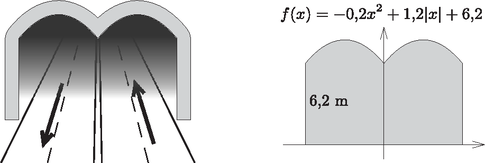

8001 + 54 = 8055

8. Egy 1240 m hosszú alagút bejáratának keresztmetszetét látjuk az ábrán egy koordinátarendszerbe helyezve, ahol az egység mindkét tengelyen 1 m. Az alagút oldalfalai 6,2 m magasak. Az alagút tetejét jó közelítéssel az

\begin{matrix} f (x) = - 0, 2 x^{2} + 1, 2 | x | + 6, 2 \end{matrix}

függvény grafikonjának egy darabja írja le.

a)

Határozzuk meg az

f (x)

függvény e részének értelmezési tartományát és értékkészletét. (8 pont)

b)

Az alagút szellőzőrendszerét úgy szeretnék megtervezni, hogy

800 m^{3}

-enként legyen egy szellőző. Hány szellőzőt kell tervezni? (8 pont)

Megoldás.

a)

f (x) = - 0, 2 x^{2} + 1, 2 | x | + 6, 2

függvény páros függvény, ezért az értelmezési tartomány és értékkészlet vizsgálatánál elegendő az

x \geq 0

esetet vizsgálnunk.
Az értelmezési tartomány meghatározásához megoldjuk az

f (x) = 6, 2

egyenletet, azaz

- 0, 2 x^{2} + 1, 2 x + 6, 2 = 6, 2

. Innen

x (- 0, 2 x + 1, 2) = 0

, vagyis

x_{1} = 0

és

x_{2} = \frac{1, 2}{0,2} = 6

. Tehát az

f (x)

függvény értelmezési tartománya:

x \in [- 6; 6]

.
A függvény értékkészletének meghatározásához ki kell számítanunk a függvény minimumának és maximumának értékét. Az

f (x) = a x^{2} + b x + c

hozzárendeléssel adott másodfokú függvény szélsőértéke az

x = - \frac{b}{2 a}

helyen van. Esetünkben a függvény szélsőértékhelye (ami most nyilvánvalóan maximumhely, mert

a < 0

) az

x = - \frac{1, 2}{- 0, 4} = 3

helyen található. A maximum értéke:

- 0, 2 \cdot 9 + 1, 2 \cdot 3 + 6, 2 = 8

. A minimum értéke:

f (- 6) = f (0) = f (6) = 6, 2

. Tehát az

f (x)

függvény értékkészlete:

f (x) \in [6, 2; 8]

b)

Ki kell számítanunk az alagút légterének nagyságát. Ez az alagút keresztmetszetének és az alagút hosszának a szorzata. A keresztmetszetet úgy kaphatjuk meg ha integráljuk az

f (x) = - 0, 2 x^{2} + 1, 2 x + 6, 2

függvényt a

[0; 6]

intervallumon, majd a kapott eredményt megszorozzuk 2-vel.

\begin{matrix} \int_{0}^{6} (- 0, 2 x^{2} + 1, 2 x + 6, 2) d x = {[- 0, 2 \cdot \frac{x^{3}}{3} + 1, 2 \cdot \frac{x^{2}}{2} + 6, 2 x]}_{0}^{6} = \\ = - 0, 2 \cdot \frac{6^{3}}{3} + 1, 2 \cdot \frac{6^{2}}{2} + 6, 2 \cdot 6 = - 14, 4 + 21, 6 + 37, 2 = 44, 4. \end{matrix}

Tehát az alagút teljes keresztmetszete: 88,8 m

^{2}

. Így az alagút légterének nagysága:

1240 \cdot 88, 8 = 110 112 m^{3}

.
Mivel

800 m^{3}

-enként kell egy szellőző, azért összesen

\frac{110 112}{800} \approx 137, 64

, azaz 138 darabot kell tervezni.

9. Négy különböző prímszámról az alábbiakat tudjuk: összegük

77

, négyzeteik összege:

4527

. Mennyi e négy prímszám szorzata? (16 pont)

Megoldás. Legyen a négy különböző prímszám

p_{1} < p_{2} < p_{3} < p_{4}

. A feltételek szerint

p_{1} + p_{2} + p_{3} + p_{4} = 77

és

p_{1}^{2} + p_{2}^{2} + p_{3}^{2} + p_{4}^{2} = 4527

. Ha négy különböző prímszám összege páratlan, akkor az egyiknek párosnak kell lennie, így

p_{1} = 2

. Ezzel

p_{2} + p_{3} + p_{4} = 75

és

p_{2}^{2} + p_{3}^{2} + p_{4}^{2} = 4523

.
Egy prímszám 3-mal osztva 1 vagy 2 maradékot ad (kivétel a 3), vagyis

p = 3 k + 1

vagy

p = 3 k + 2

. Ezek négyzete

p^{2} = 9 k^{2} + 6 k + 1

vagy

p^{2} = 9 k^{2} + 12 k + 3 + 1

. Ezzel arra jutottunk, hogy bármely prímszám négyzete (kivéve a

p = 3

esetet) 3-mal osztva 1 maradékot ad. Mivel a jobb oldal 3-mal osztva 2 maradékot ad, így a bal oldalon valamelyik prímnek oszthatónak kell lennie 3-mal, azaz

p_{2} = 3

. Ezzel a második egyenlőség így alakul:

p_{3}^{2} + p_{4}^{2} = 4514

.
Most vizsgáljuk meg a prímszámok négyzetének utolsó számjegyét. A

p = 2

és

p = 5

esetek kivételével minden prímszám utolsó számjegye 1, 3, 7 vagy 9. Ezek négyzete 1, 9, 9, 1. Tehát minden prímszám (a 2 és az 5 kivételével) négyzetének utolsó jegye 1 vagy 9. Mivel ezek közül bármely kettőt összeadva az eredmény nem lehet 4, azért ha két különböző prímszám négyzetének összege 4-re végződik, akkor az egyiknek 5-nek kell lenni:

p_{3} = 5

. Ekkor

p_{4}^{2} = 4489

, ahonnan

p_{4} = 67

, ami szintén prímszám.
Tehát a négy prímszám szorzata:

2 \cdot 3 \cdot 5 \cdot 67 = 2010