Cím: Az 51. Nemzetközi Matematikai Diákolimpia feladatainak megoldásai
Füzet: 2010/október, 386 - 393. oldal  PDF  |  MathML 

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A hagyományoknak megfelelően ebben az évben is közöljük a nyári matematikai diákolimpia feladatainak a megoldásait; lényegében úgy, ahogyan a legilletékesebbek, a magyar csapat tagjai leírták. Közreműködésüket köszönjük és ezúton is gratulálunk eredményeikhez.

 
A szerkesztőség
 

1. Határozzuk meg az összes olyan f:R→R függvényt, amelyre az f([x]y)=f(x)[f(y)] egyenlőség teljesül minden x,y∈R-re. (Itt [z] a legnagyobb olyan egész számot jelöli, amely kisebb vagy egyenlő z-nél.)
 
Mészáros András megoldása. Az azonosan nulla függvény nyilván megoldás. Vizsgáljuk meg azt az esetet, amikor van olyan t, amelyre f(t)≠0. Ekkor [f(t)] sem lehet 0, hiszen [f(t)]=0-ból az x=1, y=t helyettesítéssel f([1]t)=f(1)[f(t)]=0 következne, ami ellentmondás.
De ekkor y=t mellett x helyébe a-t, illetve [a]-t írva:
f([a]t)=f(a)[f(t)],illetvef([a]t)=f([a])[f(t)].
E kettőt kivonva egymásból: 0=[f(t)](f(a)-f([a])), és ez, mivel [f(t)] nem 0, azt jelenti, hogy minden a-ra f(a)=f([a]).
Ha bebizonyítanánk, hogy van olyan c konstans, amelyre f(n)=c minden egész n-re teljesül, akkor a fenti szerint azt kapnánk, hogy f konstans függvény. Ezt mutatjuk meg.
Legyen x=y=0, ekkor f(0)=f(0)⋅[f(0)], vagyis 0=f(0)(1-[f(0)]). Ez kétféleképpen lehetséges.
1. eset: f(0)=0. Legyen x=2a és y=12, ahol a tetszőleges egész szám. Ekkor
f([2a]⋅12)=f(2a)⋅[f(12)],def(12)=f([12])=f(0)=0,
de f(12)=f([12])=f(0)=0, így f(a)=0, minden a egészre; mint fent láttuk ez azt jelenti, hogy f azonosan 0, tehát ebben az esetben nem találtunk új megoldást.
2. eset: [f(0)]=1. Ekkor az y=0 helyettesítéssel: f([x]⋅0)=f(x)⋅[f(0)], vagyis f(0)=f(x), tehát f konstans: f(x)=c, és [c]=[f(0)]=1.
Ezzel beláttuk, hogy f vagy az azonosan nulla függvény, vagy konstans c, ahol [c]=1. Könnyen látható, hogy ezek a függvények valóban teljesítik is a feladat feltételét.
 
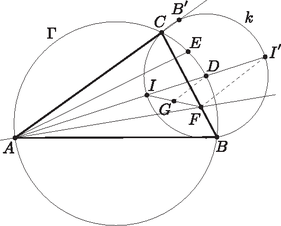
2. Legyen I az ABC háromszög beírt körének középpontja, Γ pedig a háromszög körülírt köre. Az AI egyenes másik metszéspontja a Γ körrel legyen D. Legyen E a BDC^ körív egy pontja, F pedig a BC szakasz egy pontja, amelyekre teljesül
BAF∢=CAE∢<12BAC∢.
Legyen továbbá G az IF szakasz középpontja. Bizonyítsuk be, hogy a DG és EI egyenesek a Γ körön metszik egymást.
 
Nagy Donát megoldása. Legyen I tükörképe D-re I', ekkor ID=DI', és így GD∥FI', hiszen GD középvonal az IFI' háromszögben. Mivel AD szögfelező az ABC háromszögben, a kerületi szögek tételéből BD=DC. Felhasználva, hogy BI és CI szögfelező az ABC háromszögben
BIC∢=180∘-ICB∢-IBC∢=180∘-ACB∢2-ABC∢2,továbbáBDC∢=180∘-BAC∢=ABC∢+ACB∢,
hiszen ABCD húrnégyszög. A D középpontú DB=DC sugarú körön I rajta van, hiszen BIC∢=180∘-BDC∢2, és BC elválasztja D-t és I-t. Az II' nyilván ennek a k körnek az átmérője.
 
 

Legyen FAI∢=IAE∢=φ (a két szög a feladat feltétele és IAB∢=IAC∢ miatt egyenlő). A kerületi szögek tétele szerint GD és EI metszéspontja pontosan akkor van Γ-n, ha
(GD→,IE→)∢=φ=(AD→,AE→)∢=(AI'→,AE→)∢
(itt a megfelelő vektorok által bezárt irányított szögek egyenlőségét tekintem). Mivel GD→ és FI'→ egyirányúak, ez ekvivalens azzal, hogy
(AI'→,AE→)∢=φ=(FI'→,IE→)∢.
Tekintsük azt az A középpontú φ szögű nyújtva forgatást, ami F-et I-be viszi. Ez egy φ szöggel való nyújtva forgatás, I' képe az AE egyenesre, AI' képére esik, és a bizonyítandó ekvivalens azzal, hogy FI' képe IE, tehát hogy I' képe E. Az I' képe pontosan akkor E, ha AF:AI=AI':AE, azaz AE⋅AF=AI⋅AI'.
Mivel BAF∢=EAC∢ és a kerületi szögek tételéből:
CEA∢=CBA∢,ABF∼AEC,AB:AF=AE:AC,AE⋅AF=AB⋅AC.
Így az állítás pontosan akkor teljesül, ha AB⋅AC=AI⋅AI'. Legyen B' a B pont tükörképe AD-re; ekkor BAD∢=DAC∢ miatt B' az AC egyenesen van, BD=B'D miatt B' a k körön van, és B'=C (akkor és) csak akkor teljesül, ha AB=AC, de ekkor a kerületi szögek tételéből:
ACD∢=ACB∢+DAB∢=ACB∢+180∘-2ACB∢2=90∘,
így a k kör B'=C-ben érinti az AC egyenest. Ezekből következik, hogy A-nak a k-ra vonatkozó hatványa AI⋅AI'=AC⋅AB'=AC⋅AB, és ezzel készen vagyunk.
 
3. Legyen N a pozitív egész számok halmaza. Határozzuk meg az összes olyan g:N→N függvényt, amelyre (g(m)+n)(m+g(n)) teljes négyzet minden m,n∈N-re.
 
Nagy János megoldása. Rögtön látható, hogy a g(n)=n+c alakú függvények megfelelnek a feltételnek, ahol c egy nemnegatív egész szám, hiszen ekkor a függvény értékkészlete megfelelő és
(g(m)+n)(m+g(n))=(m+n+c)2,
ami valóban mindig teljes négyzet.
Bebizonyítjuk, hogy csak ezek a jó függvények.
Nézzük meg, hogy egy tetszőleges pozitív egész m-re milyen értéket vehet fel a g(m+1)-g(m) kifejezés. Először igazolom, hogy nem lehet 2-től különböző prímosztója. Indirekt módon tegyük fel, hogy valamilyen p≠2 prímre p∣g(m+1)-g(m) és legyen g(m)=pl+r, illetve g(m+1)=pk+r. Mivel p>2, azért kettőnél több maradékosztály van, tehát létezik biztosan olyan u pozitív egész, hogy sem (u+l), sem (u+k) nem osztható p-vel. Legyen n=pu-r.
A feladat feltételéből tudjuk, hogy (g(m)+n)(m+g(n)) négyzetszám, tehát p(l+u)(m+g(n)) négyzetszám. Tudjuk, hogy (u+l) nem osztható p-vel, de p-nek páros kitevőn kell szerepelnie egy négyzetszámban, így p∣m+g(n).
Ugyanígy kapjuk m helyébe (m+1)-et írva, hogy p∣m+1+g(n), ebből p∣m+1+g(n)-m-g(n)=1, ami ellentmondás. Így tehát azt kaptuk, hogy g(m+1)-g(m)-nek semmilyen m-re nem lehet 2-től különböző prímosztója.
Most bebizonyítom, hogy g(m+1)-g(m) nem lehet osztható 4-gyel. Tételezzük fel indirekt módon, hogy 4∣g(m+1)-g(m). Ekkor létezik olyan n pozitív egész szám, hogy n+g(m) és n+g(m+1) is kettő maradékot ad 4-gyel osztva.
Tudjuk, hogy (g(m)+n)(m+g(n)) négyzetszám, de g(m)+n osztható 2-vel, de 4-gyel nem, amiből 2∣m+g(n). Ugyanígy kapjuk m helyébe (m+1)-et írva, hogy 2∣m+1+g(n), két szomszédos egész szám mindegyike nem lehet páros, tehát ellentmondásra jutottunk, tehát 4∣g(m+1)-g(m) nem teljesülhet.
Így arra jutottunk, hogy minden m-re g(m+1)-g(m) lehetséges értékei 1, -1, 2, -2.
Ezután bebizonyítom, hogy egy adott t értéket, ha t≠1, akkor csak véges sokszor veheti föl a g(m+1)-g(m) kifejezés. Tételezzük fel, hogy végtelen sok különböző m egész számra g(m+1)-g(m)=t. Vegyük észre, hogy
(g(m+1)+m)(g(m)+m+1)=(g(m)+m+t)(g(m)+m+1)
négyzetszám. Legyen v=g(m)+m+1, mivel v>m, ezért tudjuk, hogy v⋅(v+t-1) végtelen sok pozitív egész v-re négyzetszám.
Most két eset van.
1. eset: Ha t-1 páros. Ekkor
(v+t-32)2<v⋅(v+t-1)<(v+t-12)2,
ha v elég nagy, ami ellentmondás, hiszen ekkor v⋅(v+t-1) nem lehet négyzetszám. A fenti egyenlőtlenség jobb oldala egyértelmű, a bal oldal azt jelenti, hogy
v2+(t-3)v+(t-32)2<v2+v(t-1),(t-32)2<2v,
ami teljesül, ha v elég nagy.
2. eset: Ha t-1 páratlan. Ekkor
(v+t-22)2<v⋅(v+t-1)<(v+t2)2,
ha v elég nagy, ami ellentmondás, hiszen ekkor v⋅(v+t-1) nem lehet négyzetszám. A fenti egyenlőtlenség jobb oldala egyértelmű, a bal oldal azt jelenti, hogy
v2+(t-2)v+(t-22)2<v2+v(t-1),(t-22)2<v,
ami teljesül, ha v elég nagy.
Azt kaptuk, hogy egy t érték csak véges sokszor szerepelhet különbségként, ha t≠1. Így tehát a -1, 2, -2 értékek csak véges sokszor szerepelhetnek g(m+1)-g(m) értékeként, vagyis egy korláttól kezdve minden m-re g(m+1)=g(m)+1, azaz ha m>N, akkor g(m)=m+c valamilyen konstans c-re.
Továbbá bebizonyítjuk, hogy akármilyen N-nél kisebb m egész számra is g(m)=m+c. Válasszunk egy olyan n>N számot, amire m+n+c=p, ahol p egy prím, ekkor (g(n)+m)(g(m)+n) négyzetszám, de g(n)+m=p, tehát g(m)+n osztható p-vel, azaz p∣g(m)+n-p=g(m)-m-c. Azt kaptuk, hogy g(m)-m-c osztható végtelen sok elég nagy prímmel, amiből g(m)=m+c.
Így tehát minden pozitív egész m-re g(m)=m+c, ahol c egy egész szám, de nyilván nemnegatív. Ezek az egyedüli jó megoldások.
 
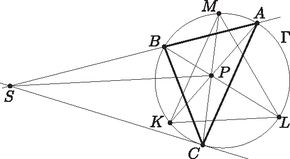
4. Legyen P egy pont az ABC háromszög belsejében. Az AP, BP és CP egyenesek másik metszéspontja az ABC háromszög Γ körülírt körével legyen rendre K, L és M. A Γ körhöz C pontban húzott érintő messe az AB egyenest az S pontban. Tegyük fel, hogy SC=SP. Bizonyítsuk be, hogy MK=ML.
 
Bodor Bertalan megoldása. Legyen BAC∢=α, ACB∢=β, CBA∢=γ, BSP∢=φ.
Az S pontnak a Γ körre vonatkozó hatványa
SA⋅SB=SC2=SP2.
Ebből SBSP=SPSA adódik, ami azt jelenti, hogy az SBP és SPA háromszögek hasonlóak egymáshoz. Ebből SAP∢=SPB∢ következik. Ekkor a kerületi szögek tételéből:
AKL∢=ABL∢=BSP∢+SPB∢=φ+SPB∢=φ+SAP∢==φ+BAK∢=φ+BLK∢,
ahonnan
AKL∢-BLK∢=φ.(1)

 
 

Az érintő szárú kerületi szögek tétele miatt BCS∢=CAB∢=α. Az ACS háromszögben a szögek összege 180∘=α+ACS∢+CSP∢+ASP∢=2α+γ+φ+CSP∢, amiből CSP∢=180∘-2α-γ-φ. SC=SP miatt az SCP háromszög egyenlő szárú, és akkor
SPC∢=SCP∢=180∘-CSP∢2=α+γ+φ2.
Ebből
BCM∢=SCP∢-BCS∢=γ+φ2ésACM∢=γ-φ2.
A kerületi szögek tételéből:
BLM∢-AKM∢=BCM∢-ACM∢=γ+φ2-γ-φ2=φ.(2)

Az (1) és (2) egyenlőségek megfelelő oldalait egymásból kivonva
AKL∢-BLK∢-BLM∢+AKM∢=0,
azaz
AKL∢+AKM∢=BLK∢+BLM∢⇔MKL∢=MLK∢⇔MK=ML
adódik, és ezt kellett bizonyítanunk.
 
5. A B1, B2, B3, B4, B5, B6 dobozok mindegyikében kezdetben egy érme van. Kétféle megengedett lépés van:
1. típusú lépés: Választunk egy Bj nemüres dobozt, ahol 1≤j≤5. Elveszünk egy érmét a Bj dobozból, és hozzáadunk két érmét a Bj+1 dobozhoz.
2. típusú lépés: Választunk egy Bk nemüres dobozt, ahol 1≤k≤4. Elveszünk egy érmét a Bk dobozból, és kicseréljük a Bk+1 (esetleg üres) doboz tartalmát a Bk+2 (esetleg üres) doboz tartalmával.
Állapítsuk meg, hogy ilyen lépések valamilyen véges sorozata segítségével elérhető-e, hogy a B1, B2, B3, B4, B5 dobozok mindegyike üres legyen, a B6 doboz pedig pontosan 201020102010 érmét tartalmazzon. (Definíció szerint abc=a(bc).)
 
Dankovics Attila megoldása. Vezessük be a következő jelöléseket.
Kapcsos zárójelbe tett rendezett számhatosok jelölik az állásokat: {1;1;1;1;1;1} az alapállás (az első pár üreset elhagyva: {0;0;0;1;1;1}={1;1;1}).
Zárójelbe tett rendezett számpárok jelölik a lépéseket: például (1;2) azt jelenti, hogy az első dobozból egy 2. típusú lépést hajtottunk végre. Végül jelölje például n⋅(k;1) azt, hogy a (k;1) lépést n-szer végezzük el.
Legyen v=201020102010.
 
1. Lemma. Az {a;b;c;x;0;0} állásból elérhető az {a;b;c;0;2x;0} állás.
 

Bizonyítás. Teljes indukció x szerint: x=1-re (4;1) lépés után elértük az állást.
Indukciós lépés: {a;b;c;0;2x-1;0} az indukciós feltevés szerint elérhető. Ez után 2x-1-szer az (5;1), majd a (4;2) lépéseket végrehajtva elértük a kívánt állást.
Hajtsuk végre egymás után a következő lépéseket:
{1;1;1;1;1;1}-re (1;1); (2;1); (3;1); (4;1); (5;1), az így kapott
{0;2;2;2;2;3}-re 2⋅(5;1); (4;2); 7⋅(5;1); (3;2), majd
{0;2;1;14;0;0}-re az 1. Lemma szerint létező lépéssorozattal kapott
{0;2;1;0;214;0}-re (3;2); (2;2); (2;1); 2⋅(3;1) adja
{0;0;214;4;0;0}-t, amire az 1. Lemma eljárását és (3;2)-t felváltva ismételgetve 214-szer a {0;0;0;222⋅⋅⋅22︸214+2db;0;0} álláshoz jutunk.
Legyen a B4 dobozban lévő érmék aktuális száma mindig h. Megjegyzendő, hogy h paritása tetszőlegesre beállítható (szükség esetén a (4;2) lépés alkalmazásával); ezt később fogom kihasználni.
Az előbbi helyzetből a 3⋅((4;1);2⋅(5;1)) átalakítás után a {h;0;12} állást kapjuk. Jelölje a B6-ban lévő érmék számát mindig y (mely jelenleg 3-mal osztható, lévén 12). Legyen végül a B5-ben lévő érmék száma x.
Ekkor a (4;2); x⋅(5;1) lépéssorozat y értékét duplázza és h értékét 1-gyel csökkenti (ezután h még pozitív marad, mert h>v; továbbá y 3-mal osztható marad; továbbá h paritása tetszőleges marad). Duplázzuk y-t míg 2y≤v<4y teljesül. Legyen az ekkor aktuális y értéke c. A (4;2) lépés után ismételjük az (5;1) lépést addig, amíg x+2y=v nem teljesül (előbb-utóbb teljesülni fog, mert x+2y minden lépésben 3-mal nő, így c és 4c között minden 3-mal osztható értéket felvesz, és v is ilyen). Ezt követően a (4;2); x⋅(5;1) lépéssorozat után a {h;0;v} állást kapjuk. Ez az állás tetszőleges paritású h-val elérhető, legyen h páros. Ekkor h⋅(4;2) után az állás: {0;0;0;0;0;v}, ami megegyezik az elérendő állással.
Tehát a kérdéses állás elérhető.
 
6. Legyen a1,a2,a3,... pozitív valós számok egy sorozata. Tegyük fel, hogy van egy olyan s pozitív egész, amellyel
an=max{ak+an-k∣1≤k≤n-1}
teljesül minden n>s egészre. Bizonyítsuk be, hogy léteznek olyan ℓ és N pozitív egészek, amikre ℓ≤s, és an=aℓ+an-ℓ minden n≥N-re.
 
Éles András megoldása. Legyen m≥2, és 1≤i1,i2,...,ik≤s tetszőleges m darab pozitív egész, melyek összege n. Ha ezek teljesítenek egy plusz feltételt, akkor az
ai1+ai2+...+aim
összeget n-re képzett összegnek nevezzük. A plusz feltétel az, hogy az ij számok közül valamelyik kettő összege nagyobb, mint s (például i1+i2>s, viszont i1+i1>s még nem elégséges feltétel). Ezt a definíciót és a plusz feltétel eredetét a most következő kulcsfontosságú lemma és annak bizonyítása fogja megmagyarázni.
 
Lemma. Az n-re képzett összegek maximuma an minden n>s esetén.
 

Ezt n-re indukcióval igazoljuk. Ha k>s, akkor n>k és az indukciós feltevés értelmében ak helyébe beírhatunk egy k-ra képzett összeget. Ugyanígy járunk el an-k-val. Az indexek összege n lesz, a plusz feltétel pedig teljesül, hiszen ak vagy an-k felírásából származik két megfelelő indexű tag, ha k>s vagy n-k>s (különben pedig ők maguk a két tag). Tehát an felírható egy n-re képzett összegként.
Már csak azt kell igazolni, hogy an fölső becslés minden n-re képzett összegre. Feltehető a plusz feltétel miatt, hogy i1+i2>s. Alkalmazva a sorozat képzési szabályát mindig a legelső tagra (amelynek indexe mindenütt nagyobb, mint s):
an=ai1+i2+...+ik≥ai1+i2+...+ik-1+ak≥ai1+...+ik-2+ak-1+ak≥...≥≥ai1+i2+ai3+...+ak≥ai1+ai2+...+aik.

Ezzel a lemmát igazoltuk.
Legyen l olyan pozitív egész, melyre 1≤l≤s és ezen belül all maximális! A megoldás azon észrevételen alapszik, hogy elég nagy n-re felírva an-et egy n-re képzett összegként, az al-től különböző tagok száma egy bizonyos határ alá szorítható. Ha ugyanis t≠l és van l+2 darab at az összegben, akkor l darab at lecserélhető t darab al-re, az összeg ekkor nem csökken, hiszen
l⋅at=lt⋅att≤lt⋅all=t⋅al.
Így egy legalább akkora, tehát ismét an-nel egyenlő n-re képzett összeget kaptunk. (azért a +2 darab at, hogy az eltűnő indexből maradjon legalább kettő, így ne sérüljön a plusz feltétel). Ezt az eljárást addig végezzük, míg lehet, ily módon an már olyan n-re képzett összegként áll majd elő, ahol minden t, 1≤t≤s, t≠l esetén at az összegben legfeljebb (l+1)-szer szerepel.
Következő választásunk
N=(1+2+...+s)(l+1)+2l+1,
ugyanis n≥N esetén an fenti felírásában legalább 3 darab al lesz jelen, hiszen a többi index összege maximum N-2l-1. Az egyik al-t törölve marad legalább kettő (így a plusz feltétel megint nem sérül), az indexek összege n-l lesz, tehát egy (n-l)-re képzett összeg, Sn-l marad hátra. De akkor, a lemma és a sorozat képzése alapján
an=al+Sn-l≤al+an-l≤an.
Ez végig egyenlőség. Tehát l-nek és N-nek a fenti választásaival an=al+an-l minden n≥N esetén. (A gondolatmenet finomításával N javítható.)