Kezdőlap


Cím:	Titkosítás fraktálok segítségével
Szerző(k):	Genda Attila
Füzet:	2014/december, 537 - 542. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

¹
A kriptográfia története évezredekre nyúlik vissza, már az ókori görögök és héberek is ismerték a rejtjelezés tudományát, a spártaiak például az úgynevezett szkütalét, a héber tudósok egyszerű monoalfabetikus (adott betű helyett más betűt írunk, de mindig ugyanazt, $a$ helyett például mindig $b$ -t) rejtjeleket használtak (atbas). Julius Caesarról elnevezett híres szintén monoalfabetikus kódolás a Caesar-rejtjel.
Az egyszerű monoalfabetikus kódok még évszázadokon át divatban voltak, amíg az arab tudósok rá nem jöttek megfejtésük módjára, az ún. statisztikus elemzésre. Ettől kezdve egy egyébként megfejthetetlen kódot egy gyakorlott kriptográfus fél óra alatt könnyűszerrel feltört.
A technika fejlődésével a kriptográfiában is mindinkább nagyobb szerepet kaptak a matematikusok, műszaki szakemberek. Így lehetséges az, hogy mára már a kriptográfiát egyesek a matematika egyik ágaként kezelik.

Néhány szó a Julia-halmazokról és a Mandelbrot-halmazról

Mi is az a Mandelbrot-halmaz? A matematikát kedvelők legnagyobb része már egész biztosan találkozott ezzel a rendkívül híres halmazzal. Sokan vannak, akik minden bizonnyal csak képről ismerik, mások pedig tisztában vannak elméleti hátterével is. Azok kedvéért, akik még nem tudják, hogy pontosan miről is van szó, egy kis kitekintőt adunk arról, hogy mire is hivatkozunk majd a későbbiekben.
Mi tartozik a halmazhoz és mi nem?
Kezdjük talán azzal, hogy az alaphalmaz a komplex számok halmaza [9]. Ezek a számok középiskolás szinten jóval kisebb szerepet kapnak, már ha egyáltalán megemlítik őket, mint például a valós vagy természetes számok. Egy komplex szám lényegesen különbözik néhány dologban egy valós számtól, azonban sok más dologban ugyanúgy viselkedik, mint valós társa.
A komplex számsíkot hívják még Gauss-féle számsíknak is, ez a megfelelője a valós számok halmazán a számok elhelyezésére használt számegyenesnek. A különbség annyi, hogy a számegyenesen egyetlen adat egyértelműen jelöli a szám helyét, míg mint a Descartes-koordinátarendszerben már megszoktuk, a komplex számokat is csak két adattal tudjuk pontosan megadni (valós rész: Re és imaginárius rész: Im), melyeket a következő alakban jelölhetünk:

z = a + b \cdot i

², ahol

a

a valós tengelyen felvett érték,

b

pedig az imaginárius (képzeletbeli) tengelyen felvett érték (

a

és

b

valós számok). Hogy mi az az

i

i

az a szám, amelynek négyzete

- 1

, azaz

i = \sqrt[]{- 1}

. Ez furcsának tűnhet első ránézésre, hiszen megszoktuk már, és belénk is nevelték, hogy a valós számok halmazán negatív számból nem vonhatunk gyököt, és bizony egy dolgozatnál súlyos pontokat is veszthetünk, ha figyelmetlenül mégis megtesszük például egy ismeretlen

x

esetén. Azonban a komplex számok halmaza éppen azért van, hogy ez a művelet értelmezhető legyen.
A komplex számokat vektorokként is kezelhetjük, így az összeadás és kivonás művelete például könnyen értelmezhető vektorösszeadásként/kivonásként is. A szorzás sem bonyolult, hasonlóan kezelendő mint két kéttagú polinom szorzása:

\begin{matrix} (a + b \cdot i) \cdot (c + d \cdot i) = a \cdot c + a \cdot d \cdot i + b \cdot i \cdot c + b \cdot d \cdot i^{2}, \end{matrix}

i^{2} = - 1

, azaz

(a + b \cdot i) \cdot (c + d \cdot i) = a \cdot c + (a \cdot d + b \cdot c) \cdot i - b \cdot d

.
Ha a kedves olvasó még több műveletre kíváncsi, akkor az [1], vagy a [2] oldalakon sok érdekességet találhat.
A matematikában a Mandelbrot-halmaz azon

c

komplex számokból áll (a ,,komplex számsík'' azon pontjainak mértani helye, halmaza), melyekre az alábbi (komplex szám értékű)

x_{n}

rekurzív sorozat:

\begin{matrix} x_{1} : = c, x_{n + 1} : = {(x_{n})}^{2} + c \end{matrix}

nem tart végtelenbe, azaz abszolút értékben (hosszára nézve) korlátos [3].
Legyen

c = konstans

;

f (x) = x^{2} + c

dinamikus függvény minden

x_{1}

komplex számhoz. Azon

x_{1}

értékek halmazát, amelynél az

f (x) = x^{2} + c

rekurziója

c = konstans

mellett nem tart a végtelenhez, Julia-halmaznak hívjuk. Minden egyes

c

értékhez tartozik egy Julia-halmaz [4], azaz a Mandelbrot-halmaz definíciójától annyi a különbség, hogy ott

c

minden pontra változik, itt azonban minden pont esetén egy adott konstans.
Ezeket a halmazokat ki is rajzoltathatjuk a számítógépünk segítségével. Általában feketével jelölik azokat a pontokat, amelyek a halmaz részei, és valamilyen egyéb színnel azokat, amelyekről bizonyos lépésszám után kiderül, hogy mégsem a halmaz részei, ezek kirajzolásáról a későbbiekben még lesz szó. A halmazokról még sok érdekesség olvasható például itt: [5], [6], [7], [8], és még rengeteg más oldalon, idegen nyelven is.

A programról

Az általam írt programban én is a matematika, itt nevezetesen a káoszelmélet által is tárgyalt fraktálok adta lehetőségeket szerettem volna kihasználni úgy, hogy a kódoláshoz szükséges kulcs lehetőleg minimális legyen, de a lehetőségek száma mégis túl nagy ahhoz, hogy próbálgatással feltörhessék.
A program kihasználja azt, hogy bizonyos esetekben a nemlineáris rendszereknél az eredmények nem jósolhatóak meg biztonságosan előre, mint mondjuk az időjárásban, ahol például az időjárás nem azért nem mondható meg pontosan hosszabb időre előre, mert a számítógépeink teljesítménye kevés lenne a kiszámításukhoz, hanem azért, mert rendkívül apró összetevők is, amelyeknek felmérése lehetetlen, képesek döntő módon befolyásolni a végeredményt (lásd Pillangó-hatás).
A program elve a következő:

1.	A számítógép generál egy fraktált, vagy annak egy részletét az általunk megadott paraméter segítségével.

2.	A képernyőn ezt számunkra is láthatóvá teszi, így eldönthetjük, hogy alkalmas lesz-e számunkra az adott halmaz. (Minél részletgazdagabb, annál megbízhatóbb lesz majd.)

3.	A fraktál segítségével titkosítja az általunk megadott szöveget.

A program a Mandelbrot-halmazt és Julia-halmazokat tud kirajzolni, ezekre ránagyítani. A fraktál kirajzolásához természetesen nem deríthetjük ki a sík minden pontjáról, hogy a része-e a halmaznak, vagy sem. A program ezért csak a képernyőn látható

800 \times 600

pixelt tartalmazó kép képpontjaihoz hozzárendelt értékekre végzi el a számításokat. Ezekre a pontokra a program még az elején kiszámítja, hogy a halmaz részei-e, úgy, hogy az általunk kiválasztott tartományt egyenletesen felosztja 800, illetve 600 részre. Természetesen nagyításkor ez a felosztás megváltozik, és az új felosztás már a nagyítás mértékétől függően, azzal arányosan kisebb közökre osztja két pixel között a távolságokat.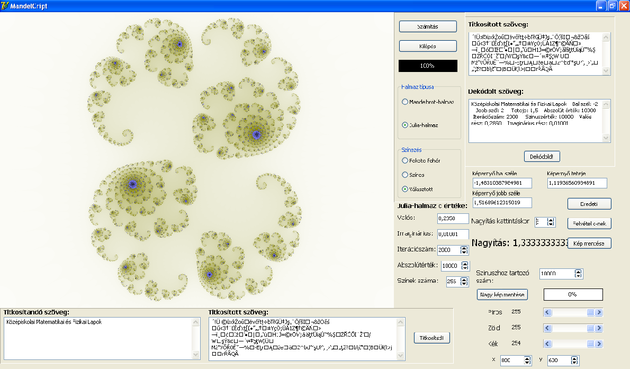

Ezután kezdi el a program az egyes pontok vizsgálatát. Mind a 480 000 ponton végigmegy egyesével. Mindegyik pontra kiszámolja a

x_{1} = c

x_{n} = x_{n - 1}^{2} + c

, rekurzív sorozat általunk kiválasztott számú első elemét, ahol Mandelbrot-halmaz esetén

c = x_{1} = a + b \cdot i

komplex szám, az adott pont kezdőértéke, míg Julia-halmaznál

x_{1}

-et ugyanúgy, a vizsgált síkrészlet egyenletes felosztásával kapjuk meg, míg

c

-t mi magunk választjuk, a képzés során mindvégig ezt a számot adjuk hozzá minden pixel esetén minden sorozattaghoz.
Két eset lehetséges, ha

n \to \infty

1.	Egy pont origótól vett távolsága is tart a végtelenhez, vagy

2.	Az origótól vett távolság nem tart végtelenhez, kettőnél kisebb abszolút értéken belül marad (Benoit Mandelbrot megállapította, hogy ha kettőnél nagyobb lesz, akkor biztosan a végtelenhez tart).

Az utóbbi pontokat vesszük a Mandelbrot-halmaz, illetve a Julia-halmazok elemeinek, ezeket a program feketére színezi, míg azokat a pontokat, amelyek nem elemei a halmaznak színesre festi, a szín attól függ, hogy az adott pixelhez tartozó ponttal számított sorozat hányadik eleme lesz az, melynek távolsága az origótól nagyobb lesz a kettő (vagy az általunk választott) értéknél.
Annak érdekében, hogy ne ütközzünk végtelen ciklusba, nem számíthatjuk a sorozatot végtelen elemig, így kiválasztunk egy számot. Ez a szám lesz az, ahányadik elemig kiszámoljuk a sorozatot. Ha a sorozat ezen elemének is kisebb lesz az origótól való távolsága, mint amit megadtunk, akkor úgy veszi a program, hogy ez a pont is a halmaz eleme. A módszer hátránya, hogy olyan pontokat is a halmaz részévé nyilvánít, amelyek lehet, hogy nem is azok. Minél nagyobb számot választunk, annál jobban fog hasonlítani az eredmény a tényleges halmazra, de azt soha nem kapjuk meg.
Azoknál a pontoknál, ahol előbb kiderül, hogy a pont a végtelenbe tart, ott nem számítja ki a program a további pontokat, hiszen ez felesleges volna.
Ezzel a módszerrel tehát minden ponthoz hozzárendelhetünk egy

k

természetes számot, mely azt jelzi, hogy a pont hány iterációs lépés után hagyta el a megadott abszolút értékű környezetet. A paramétereket variálva hamar kiderül, hogy már kis változtatásokkal is nagy különbségek adódnak a

k

-kon. Ha ezeket a

k

-kat soronként összeadjuk, akkor ez a különbség megnyolcszázszorozódik, nagyon érzékeny lesz a kezdeti paraméterekre, amelyek Mandelbrot-halmaz esetén a nagyítás és annak helye, abszolút érték és iterációk száma, Julia-halmaz esetén pedig ezeken felül a választott

c

paraméter valós és imaginárius része.
A szöveg kódolása innentől már gyerekjáték, minden karakterhez hozzárendelünk egy függvény segítségével egy sort a képernyőről (én itt egy szinusz-függvényt választottam, tekintetbe véve, hogy nem lesz periodikus, de az egyes sorok gyakorisága ugyanannyi marad, mintha egymás után vennénk a sorokat), az itt található 800 pixelhez tartozó

k

számokat összeadjuk, majd a karakter ASCII-kódjához hozzáadjuk az így kapott összeget. Hogy az így kapott számhoz hozzárendelhessünk egy ASCII karaktert 255-tel osztjuk maradékosan, így már 0 és 255 között számot kapunk maradékul, ez lesz az új, titkosított karakter.
A metódus egy kicsivel bonyolultabb, mivel 0, mint ASCII-kód esetén a program abbahagyja a titkosítást, és a további karaktereket nem kódolja, így kénytelenek vagyunk megoldani, hogy az 1

...

255 tartományba essen az új szám, de lényegében a módszer itt is ugyanaz, maradékos osztás 255-tel, majd 1 hozzáadása. Hogy elkerüljük az adatvesztés lehetőségét, itt egy kisebb trükkel éltem. A program nem tudja titkosítani a 244-es számú karaktert, de cserében nem okoz olyan végzetes hibát, hogy az eggyel nagyobb ASCII kódú karaktert adja vissza eredményül (a következő üzenethez való új kulcs megadásakor ez végzetes lehetne, ha a kulcs valamelyik számjegye helyett írna eggyel nagyobbat). Remélhetőleg ez a karakter azonban senkinek sem fog túlságosan hiányozni.
A dekódolás szimmetrikus, fordítva végzi el a műveleteket a program. A kód további erősítésére és annak elkerülésére, hogy periodikusan ismétlődjön az eltolás mértéke, egy szinusz-függvény segítségével rendeli a karakterekhez a sorokat a program.
Először kattintsunk a Számítás gombra, ezután megkapjuk a fraktált. Ha nagyítani szeretnénk, akkor a képre kattintva tehetjük.
Legyen itt egy példa a paraméterek érzékenységére: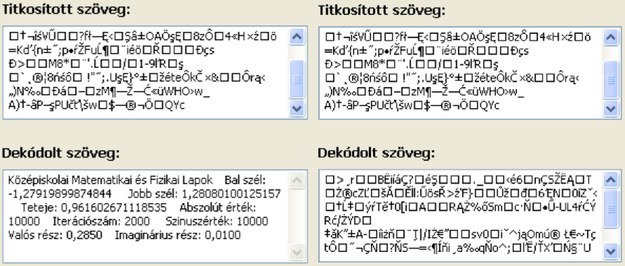

A két esetben a kulcsok egy kivételével mind megegyeznek, az eltérés annyi, hogy az első esetben az imaginárius rész

0, 01 \cdot i

, míg a másodikban

0, 010 01 \cdot i

.
Látható, hogy kis változtatások is nagy befolyással vannak a kódolásra, ez a program legnagyobb előnye, emiatt elég kevés kulcs megadása is. Lehetőség nyílik arra is, hogy a felhasználók a kulcsaikat üzenetenként lecseréljék, és újakat adjanak meg. Ha valakinek megtetszik a fraktál, akkor pedig egy gombnyomással elmentheti a számítógépére. Ha jobb minőséget szeretne, akkor pedig a kívánt felbontásra állíthatja be magának az értékeket.
A program során egy olyan titkosító program létrehozása volt tehát a cél, ami könnyen kezelhető, és kellően megbízható ahhoz, hogy idegenek elől elrejtsük üzeneteink tartalmát.

Források

[1]	http://www.math.bme.hu/ $\sim$ bfarkas/komplex.pdf.

[2]	http://hu.wikipedia.org/wiki/Komplex_számok.

[3]	http://hu.wikipedia.org/wiki/Mandelbrot-halmaz.

[4]	http://freeweb.deltha.hu/gyarmati.dr.hu/lectures/mandelbrot1.pdf, 7. oldal alja.

[5]	http://freeweb.deltha.hu/gyarmati.dr.hu/lectures/mandelbrot1.pdf.

[6]	Kecskés Lajos: Egy ölnyi végtelen, Nemzeti Tankönyvkiadó (Budapest, 2002).

[7]	http://hu.wikipedia.org/wiki/Mandelbrot-halmaz.

[8]	https://dea.lib.unideb.hu/dea/bitstream/handle/2437/2385/diplomamunka.pdf?sequence=1.

[9]	Surányi János: Ismerkedjünk a komplex számokkal, KöMaL 2 (1948), 65‐71., 5 (1948), 94‐101., 9 (1948), 131‐144., db.komal.hu/scan.

¹A szerző az itt bemutatott programmal a 23. Ifjúsági Tudományos és Innovációs Tehetségkutató Verseny III. díját nyerte és elnyerte a legjobb informatikai pályázatnak járó díjat (http://www.innovacio.hu/3a_hu_23_vegeredmeny.php).

²Emellett a jelölés mellett létezik az ún. trigonometrikus alak, ami a polárkoordinátás jelölést takarja, azaz $z = r \cdot (cos φ + (s i n φ) \cdot i)$ és exponenciális alak $z = r \cdot e^{i φ}$ .