Kezdőlap


Cím:	A hídkapcsolás eredő ellenállása és áramerősségei
Szerző(k):	Légrádi Imre
Füzet:	2016/február, 105 - 110. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek, Hídkapcsolás

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az öt ellenállásból készített szokványos hídkapcsolás eredő ellenállását többnyire csak a konkrét számértékek ismerete mellett szoktuk meghatározni. Ha azonban vesszük a fáradságot és levezetjük általános jelekkel (paraméterekkel), akkor ‐ megfelelő átalakítások után ‐ egy viszonylag egyszerű képlethez jutunk. Az alábbiakban ezt a számolást végezzük el.¹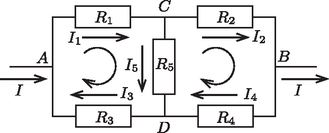
A kapcsolás, a szokásos jelölésekkel, az 1. ábrán látható. A huroktörvényt és a csomóponti törvényt alkalmazva írunk fel egyenleteket. A két hurok körüljárási irányát a görbe nyilak jelzik. Végcélunk az öt ellenállásból álló egyenáramú áramköri kapcsolás ábrán jelzett $A$ és $B$ pontok közötti $R_{A B}$ eredő ellenállásának meghatározása általános képlettel.

1. ábra

A bal oldali hurokban

\begin{matrix} I_{1} R_{1} + I_{5} R_{5} + I_{3} R_{3} = 0, \end{matrix}

(1)

a jobb oldali hurokban

\begin{matrix} - I_{5} R_{5} + I_{2} R_{2} + I_{4} R_{4} = 0. \end{matrix}

(2)

C

csomópontban

\begin{matrix} I_{1} - I_{2} - I_{5} = 0, \end{matrix}

(3)

D

csomópontban

\begin{matrix} I_{5} + I_{4} - I_{3} = 0, \end{matrix}

(4)

és végül a

B

csomópontban

\begin{matrix} I_{2} - I - I_{4} = 0. \end{matrix}

(5)

A

pontban befolyó és a

B

pontban kifolyó áram

I

erősségét mint paramétert kezeljük, így a fenti öt egymástól független egyenlet elegendő az öt ismeretlen áramerősség meghatározásához.
Egy lehetséges lépéssorozat a következő: A (3) és (5) csomóponti egyenletek összeadásával kapjuk, hogy

\begin{matrix} I_{1} = I + I_{4} + I_{5} . \end{matrix}

D

csomóponti egyenletből

I_{3} = I_{4} + I_{5}

. Ezeket az első hurokegyenletbe beírva

\begin{matrix} I_{1} R_{1} + I_{4} R_{1} + I_{5} R_{1} + I_{4} R_{3} + I_{5} R_{3} = 0 \end{matrix}

adódik. A második hurokegyenletet a

B

csomóponti összefüggés alapján

I_{2} = I + I_{4}

helyettesítéssel átírva ezt kapjuk:

\begin{matrix} - I_{5} R_{5} + I R_{2} + I_{4} R_{2} + I_{4} R_{4} = 0. \end{matrix}

Így most már csak két ismeretlenünk van, két független egyenlettel. Kiemelések után ez a két egyenlet:

\begin{matrix} \begin{matrix} (R_{1} + R_{3}) I_{4} & + (R_{1} + R_{3} + R_{5}) I_{5} & = - R_{1} I, \\ (R_{2} + R_{4}) I_{4} & - R_{5} I_{5} & = - R_{2} I . \end{matrix} \end{matrix}

Az egyenletrenszer megoldása:

\begin{matrix} I_{4} & = - \frac{R_{1} R_{5} + R_{2} (R_{1} + R_{3} + R_{5})}{(R_{1} + R_{3}) R_{5} + (R_{2} + R_{4}) (R_{1} + R_{3} + R_{5})} I, \\ I_{5} & = \frac{R_{2} (R_{1} + R_{3}) - R_{1} (R_{2} + R_{4})}{(R_{1} + R_{3}) R_{5} + (R_{2} + R_{4}) (R_{1} + R_{3} + R_{5})} I . \end{matrix}

Megjegyzés. Itt most érdemes kitérni arra a kérdésre, hogy milyen feltételek mellett lesz

I_{5}

értéke zérus. A legutóbbi képlet számlálójából következik, hogy ez akkor áll fenn, ha

\begin{matrix} \frac{R_{2}}{R_{4}} = \frac{R_{1}}{R_{3}} . \end{matrix}

Ez az eset a régi időkben használt Wheatstone-híd nevű ellenállásmérő kapcsolás megfelelője. E kapcsolásban

R_{5}

helyén egy érzékeny áramerősség-mérő műszer van,

R_{1}

helyére illesztjük a megmérendő ellenállást,

R_{2}

helyén ismert értékű etalon ellenállás helyezkedik el, és

R_{3}

R_{4}

egyetlen drótszál azon két részének ellenállása, amelyek a műszer csúsztatható

D

pontbeli csatlakozásától az

A

, illetve

B

pontig tartanak. A műszer

D

pontbeli csatlakozását ide-oda csúsztatva, megkeressük azt a helyét, amely mellett a műszeren átfolyó

I_{5}

erősségű áram zérus értékű. Ekkor fennáll a fenti aránypár, amiből

R_{1} = (R_{3} / R_{4}) R_{2}

. Minthogy

R_{3}

és

R_{4}

ugyanazon huzal két darabja, ezért ellenállásuk pontosan hosszúságukkal arányos, tehát ellenállásaik hányadosa is megegyezik hosszúságaik hányadosával. E hosszúságokat pedig egyszerűen mérhetjük. Így az ismeretlen ellenállás értékét könnyen megkapjuk az etalon értékének ismeretében:

\begin{matrix} R_{1} = \frac{ℓ_{3}}{ℓ_{4}} R_{2} . \end{matrix}

Természetesen a fenti képletünk azt is kifejezi, hogy

I_{5}

értéke akkor is zérus, ha az

R_{5}

jelű áthidaló ellenállás értéke ,,végtelen nagy''. A képletben

R_{5}

a nevező mindkét tagjában szerepel, a számlálóban pedig nem, így, ha

R_{5}

végtelen nagy értékhez tart, akkor a tört értéke nullához tart. Ez a gyakorlatban annak felel meg, hogy a

C

és a

D

pontokat nem köti össze semmilyen vezető sem. Azt is mondhatnánk, hogy ilyenkor

R_{5}

a két pont közötti levegő vagy egyéb szigetelőanyag végtelenül nagynak tekinthető ellenállása.

Visszatérve a számításokhoz,

I_{4}

és

I_{5}

ismeretében megkapjuk

I_{3}

értékét:

\begin{matrix} I_{3} = I_{4} + I_{5} = \frac{R_{2} (R_{1} + R_{3}) - R_{1} (R_{2} + R_{4}) - R_{1} R_{5} - R_{2} (R_{1} + R_{3} + R_{5})}{(R_{1} + R_{3}) R_{5} + (R_{2} + R_{4}) (R_{1} + R_{3} + R_{5})} I, \end{matrix}

B

csomópontra felírt Kirchhoff-összefüggésből

\begin{matrix} I_{2} & = I + I_{4} = \\ = \frac{R_{5} (R_{1} + R_{3}) + (R_{2} + R_{4}) (R_{1} + R_{3} + R_{5}) - R_{1} R_{5} - R_{2} (R_{1} + R_{3} + R_{5})}{(R_{1} + R_{3}) R_{5} + (R_{2} + R_{4}) (R_{1} + R_{3} + R_{5})} I, \end{matrix}

és végül a

C

csomópontnál érvényes összefüggésből

\begin{matrix} I_{1} & = I_{2} + I_{5} = \\ = \frac{(R_{2} + R_{5}) (R_{1} + R_{3}) + (R_{2} + R_{4}) (R_{3} + R_{5}) - R_{1} R_{5} - R_{2} (R_{1} + R_{3} + R_{5})}{(R_{1} + R_{3}) R_{5} + (R_{2} + R_{4}) (R_{1} + R_{3} + R_{5})} I . \end{matrix}

Mindezek ismeretében meghatározhatjuk a hídkapcsolásunk

A

és

B

pontjai között érvényes ellenállását, mert

R_{A B} = U_{A B} / I

, de

U_{A B}

-t megkapjuk, ha az

A

pontból a

B

pontba vezető valamelyik úton összegezzük a feszültségeséseket. A legegyszerűbb út az

R_{1}

és

R_{2}

ellenállásokon keresztül vezet, tehát

\begin{matrix} U_{A B} = I_{1} R_{1} + I_{1} R_{2} . \end{matrix}

(6)

Így a keresett ellenállásérték:

\begin{matrix} R_{A B} & = & \frac{R_{1} (R_{2} + R_{5}) (R_{1} + R_{3}) + R_{1} (R_{2} + R_{4}) (R_{3} + R_{5}) - R_{1}^{2} R_{5}}{(R_{1} + R_{3}) R_{5} + (R_{2} + R_{4}) (R_{1} + R_{3} + R_{5})} + \\ + \frac{- R_{1} R_{2} (R_{1} + R_{3} + R_{5}) + R_{2} R_{5} (R_{1} + R_{3})}{(R_{1} + R_{3}) R_{5} + (R_{2} + R_{4}) (R_{1} + R_{3} + R_{5})} + \\ + \frac{R_{2} (R_{2} + R_{4}) (R_{1} + R_{3} + R_{5}) - R_{1} R_{2} R_{5} - R_{2}^{2} (R_{1} + R_{3} + R_{5})}{(R_{1} + R_{3}) R_{5} + (R_{2} + R_{4}) (R_{1} + R_{3} + R_{5})} . \end{matrix}

Ezt tulajdonképpen végeredményünknek tekinthetnénk, de érdemes elvégezni a szorzásokat és összevonásokat mind a számlálókban, mind a nevezőkben és egyetlen törtben foglani össze az eredményt:

\begin{matrix} R_{A B} = \frac{R_{1} R_{2} R_{3} + R_{1} R_{2} R_{4} + R_{1} R_{3} R_{4} + R_{1} R_{3} R_{5} + R_{1} R_{4} R_{5} + R_{2} R_{3} R_{4} + R_{2} R_{3} R_{5} + R_{2} R_{4} R_{5}}{R_{1} R_{2} + R_{1} R_{4} + R_{1} R_{5} + R_{2} R_{3} + R_{2} R_{5} + R_{3} R_{4} + R_{3} R_{5} + R_{4} R_{5}} . & (*) \end{matrix}

Képletünk, monoton egyszerűsége miatt, arra is alkalmas, hogy programozható zsebkalkulátorunkba egyszerű programlépésekkel beírjuk; de még a fejben való megjegyzése sem nagyon kényelmetlen. Ez utóbbit segítheti, ha a

(*)

képlet számlálójának is és a nevezőjének is egy-egy gráfot feleltetünk meg. A gráf csúcspontjait számozzuk meg az ellenállások indexeinek megfelelő számokkal. A nevezőben szereplő szorzatok indexpárjainak megfelelő csúcspontokat kössük össze egy-egy folytonos vonallal, egy másik gráfon pedig szaggatott vonallal azokat a csúcspontokat kössük össze, amelynek megfelelő indexű ellenállások nem szerepelnek a számláló háromtényezős szorzataiban (2. ábra).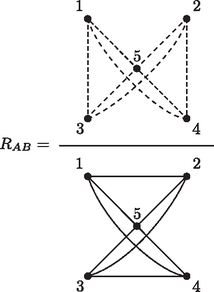

2. ábra

A rajz jól mutatja a hídkapcsolás azon szimmetriáját, hogy

R_{A B}

nem változik meg, ha az elrendezést akár a ,,függőleges'', akár a ,,vízszintes'' szimmetriatengelyére tükrözzük, vagyis végrehajtjuk az

\begin{matrix} R_{1} \leftrightarrow R_{2} és R_{3} \leftrightarrow R_{4}, \end{matrix}

(7)

vagy az

\begin{matrix} R_{1} \leftrightarrow R_{3} és R_{2} \leftrightarrow R_{4} \end{matrix}

(8)

felcseréléseket.

R_{A B}

levezetett képletének ellenőrzésére (ami egy ilyen hosszú számolás után mindenképpen célszerű) számos lehetőség kínálkozik. Nézzük meg, mekkora az eredő ellenállás, ha a hidat képező

R_{5}

ellenállás értéke zérus, ami egyszerűen azt jelenti, hogy a

C

és

D

pontokat egyesítettük (rövidre zártuk). Ekkor

R_{1}

és

R_{3}

párhuzamos kapcsolásban van, hasonlóan az

R_{2}

és

R_{4}

ellenállás is, és a két ellenálláspár sorba van kapcsolva. A könnyen megkapható eredő tehát

\begin{matrix} R_{A B} = \frac{R_{1} R_{3}}{R_{1} + R_{3}} + \frac{R_{2} R_{4}}{R_{2} + R_{4}} . \end{matrix}

Ha a

(*)

végképletünkbe is

R_{5} = 0

értéket helyettesítünk, ugyanezt az eredményt kapjuk.
Második ellenőrzésként tekintsük azt az esetet, ha nincsen a kapcsolásban hidat képező

R_{5}

jelű ellenállás, tehát nem is kapcsoltuk össze a

C

és

D

pontokat. Ilyenkor

R_{1}

és

R_{2}

közvetlenül sorosan vannak kapcsolva, hasonlóan

R_{3}

és

R_{4}

is, majd a belőlük alkotott két ellenállás van párhuzamosan kapcsolva

A

és

B

pontok közé. Ebben az esetben is könnyen kiszámítható az eredőjük:

\begin{matrix} R_{A B} = \frac{(R_{1} + R_{2}) (R_{3} + R_{4})}{(R_{1} + R_{2}) + (R_{3} + R_{4})} = \frac{R_{1} R_{3} + R_{1} R_{4} + R_{2} R_{3} + R_{2} R_{4}}{R_{1} + R_{2} + R_{3} + R_{4}} . \end{matrix}

Ha végképletünkkel ezt az esetet is ellenőrizni kívánjuk, akkor a hiányzó hidat végtelen nagy ellenállásnak kell gondolnunk, azaz keresnünk kell, hogy mely értékhez tart

R_{A B}

, ha benne

R_{5}

tart a végtelenhez. Ha a

(*)

képletünkben mind a számlálót, mind a nevezőt osztjuk

R_{5}

-tel, majd vesszük a tört határértékét, akkor ezt kapjuk:

\begin{matrix} {lim}_{R_{5} \to \infty}^{} = \frac{R_{1} R_{3} + R_{1} R_{4} + R_{2} R_{3} + R_{2} R_{4}}{R_{1} + R_{2} + R_{3} + R_{4}}, \end{matrix}

tehát a képletünk ebben az esetben is megállta helyét.
Ha a hídkapcsolás

R_{A B}

eredő ellenállásának meghatározása után az egyes elemeiben folyó áram erősségét akarjuk meghatározni abban az esetben, amikor az

A - B

pontokban csatlakoztatunk hozzá egy

U_{0}

üresjárási feszültségű és

R_{0}

belső ellenállású áramforrást (3. ábra), akkor a következőket kell tennünk.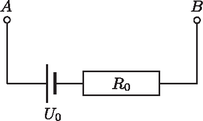

3. ábra

Meg kell határoznunk az

U_{A B}

feszültséget. Minthogy

R_{A B}

-t már kiszámítottuk a

(*)

képletünkkel, írhatjuk, hogy

\begin{matrix} U_{A B} = U_{0} - I R_{0}, ahol I = \frac{U_{A B}}{R_{A B}}, \end{matrix}

amiből

\begin{matrix} U_{A B} = \frac{R_{A B}}{R_{0} + R_{A B}} U_{0} . \end{matrix}

(9)

A kapcsolás ellenállásain folyó áramokra (amelyeket az 1. ábrán jelölt, feltételezett irányokban tekintjük pozitívnak) fennállnak az (1)‐(5) egyenlőségek, továbbá (6) és (9), valamint

U_{A B} = I R_{A B},

ahol

R_{A B}

(*)

képlettel megadott kifejezés. Ennek az egyenletrendszernek a megoldása pl. az

R_{2}

és az

R_{5}

ellenállásokon átfolyó áram erősségére:

\begin{matrix} I_{2} & = \frac{(R_{5} R_{A B} - R_{1} R_{4}) U_{0}}{[(R_{1} + R_{2}) R_{5} + (R_{2} + R_{4}) R_{1}] (R_{0} + R_{A B})}, & (10) \\ I_{5} & = \frac{[(R_{2} + R_{4}) R_{A B} - (R_{1} + R_{2}) R_{4}] U_{0}}{[(R_{1} + R_{2}) R_{5} + (R_{2} + R_{4}) R_{1}] (R_{0} + R_{A B})} . & (11) \end{matrix}

Ezekből a többi áramerősség is kiszámolható, hiszen

I_{1} = I_{2} + I_{5}

I_{3} = I_{1} - I

I_{4} = I_{3} - I_{5}

Megjegyzés. Az

I_{1}

I_{3}

és

I_{4}

áramerősségeket a (10) képlet alapján is kiszámíthatjuk, ha alkalmazzuk a (7) vagy (8), esetleg mindkettő átnevezés lehetőségét. Ezzel a transzformációval elérhetjük, hogy az

R_{1}

R_{3}

és

R_{4}

ellenállások bármelyike a kapcsolás jobb felső (eredetileg

R_{2}

-vel jelzett) ellenállásának helyére kerüljön, és ezután már alkalmazhatjuk a (10) képletet. Vigyázat: a (7) transzformáció során

I_{5}

kivételével valamennyi áram előjele megváltozik.

I_{5}

áramerősségre, vagyis a hidat képező

R_{5}

ellenálláson folyó áram erősségére vonatkozólag ismét felvethetjük a már előzőleg említett, kiegyensúlyozott Wheatstone-híd esetét, amelynél fennáll, hogy

R_{1} / R_{2} = R_{3} / R_{4}

. Ekkor, természetesen

\begin{matrix} R_{A B} = \frac{(R_{1} + R_{2}) (R_{3} + R_{4})}{R_{1} + R_{2} + R_{3} + R_{4}}, \end{matrix}

(12)

vagyis

R_{5}

-nek nincsen szerepe a hídkapcsolás eredőjében, nullának vagy akár végtelen nagynak tekinthető.
Ellenőrizzük, hogy a (11) képletünk ez esetben valóban zérus áramerősségértéket ad-e. A választ a képlet számlálójában a szögletes zárójelben lévő kifejezés, annak várható eltűnése adja meg. Ebbe beírva

R_{A B}

(12)-beli értékét, ezt kapjuk:

\begin{matrix} (R_{2} + R_{4}) R_{A B} - (R_{1} + R_{2}) R_{4} = \frac{(R_{2} + R_{4}) (R_{1} + R_{2}) (R_{3} + R_{4})}{R_{1} + R_{2} + R_{3} + R_{4}} - (R_{1} + R_{2}) R_{4} . \end{matrix}

Elvégezve a közös nevezőre hozást, a szorzásokat, összevonásokat, az új tört számlálójának ezt kapjuk:

\begin{matrix} R_{1} R_{2} R_{3} + R_{1} R_{2} R_{4} + R_{2} R_{4}^{2} - R_{1}^{2} R_{4} - R_{1} R_{2} R_{4} - R_{2} R_{4}^{2} = R_{1} (R_{2} R_{3} - R_{1} R_{4}) = 0. \end{matrix}

Az utolsó lépésnél figyelembe vettük, hogy

R_{1} / R_{2} = R_{3} / R_{4}

. Látjuk, hogy (11) számlálója zérus, tehát valóban igaz, hogy

I_{5} = 0

¹A paraméteres képletnek megvan az az előnye, hogy csak egyszer kell kiszámítanunk, a továbbiakban már csak alkalmazzuk. Ugyanígy járunk el pl. a másodfokú egyenlet megoldóképletével is; azt is elegendő egyszer levezetni, utána pedig már akárhányszor alkalmazhatjuk.