Cím:	Megoldásvázlatok a 2014/9. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Ratkó Éva ,  Schmieder László
Füzet:	2015/január, 3 - 9. oldal	PDF  |  MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Jenci rollert szeretne vásárolni, ezért elindul a boltba valamennyi pénzzel, mind három fabatkás. A boltban csak egyfajta roller van, az ára $19$ fabatka. A boltosnak azonban csak öt fabatkásai vannak. Hogyan tudják a legkevesebb pénzdarab fölhasználásával lebonyolítani az üzletet?  (11 pont)   Megoldás. A háromfabatkások száma legyen $x$, az ötfabatkásoké pedig $y$. Ekkor $3x-5y=19$. Ebből $x$-et kifejezve kapjuk, hogy $\begin{array}{c}{\displaystyle x=\frac{5y+19}{3}=y+6+\frac{2y+1}{3}\mathrm{.}}\end{array}$ Mivel $x$ és $y$ egész számok, ezért $\frac{2y+1}{3}$ is egész, vagyis $3\mid 2y+1$. Ez pontosan akkor teljesül, ha $y=3k+1$. Ha $y=3k+1$, akkor $\begin{array}{c}{\displaystyle x=y+6+\frac{2y+1}{3}=3k+1+6+\frac{2\left(3k+1\right)+1}{3}=3k+7+2k+1=5k+8.}\end{array}$ A legkisebb megoldást akkor kapjuk, ha $k=0$. Ekkor $x=8$, $y=1$, vagyis Jenci 8 darab háromfabatkással fizet és 1 darab ötfabatkást kap visszajárónak.   2. Három szomszédos páratlan négyzetszám összege egy csupa azonos számjegyből álló négyjegyű szám. Határozzuk meg a négyjegyű számot.  (12 pont)   Megoldás. Felírhatjuk a következő egyenletet: $\begin{array}{c}{\displaystyle {\left(2a-1\right)}^2+{\left(2a+1\right)}^2+{\left(2a+3\right)}^2=\overline{bbbb}\mathrm{,}}\end{array}$ ahol $a\in {\text{N}}^{+}$, $b\ne 0$ pedig számjegy. A jobb oldal alakítható: $\begin{array}{c}{\displaystyle \overline{bbbb}=1111\cdot b=11\cdot 101\cdot b\mathrm{.}}\end{array}$ A bal oldalon a zárójeleket felbontva és a tagokat összevonva kapjuk, hogy: $\begin{array}{c}{\displaystyle 12a^2+12a+11=11\cdot 101\cdot b\mathrm{.}}\end{array}$ Mivel a jobb oldal osztható 11-gyel, ezért a bal oldal is: $11\mid 12a^2+12a+11$, amiből következik, hogy $11\mid 12a^2+12a$. Mivel $\left(\mathrm{11,12}\right)=1$, ezért innen $11\mid a^2+a$ következik. Mivel $a^2+a=a\left(a+1\right)$, ezért vagy $a$, vagy $a+1$ a 11 többszöröse. Azt is tudjuk, hogy $f\left(a\right):=12a^2+12a+11$ értéke legfeljebb 9999, és hogy pozitív egész $a$ esetén $f\left(a\right)$ szigorúan monoton nő. Vizsgáljuk meg a szóba jövő eseteket. Ha $a=10$, akkor $f\left(a\right)=1331$. ha $a=11$, akkor $f\left(a\right)$ értéke 1594. Ha $a=21$, akkor $f\left(a\right)$ értéke 5555, illetve ha $a=22$, akkor $f\left(a\right)=6083$. Ha $a=32$, akkor $f\left(a\right)$ már ötjegyű, tehát más megoldás nem lehetséges. Tehát a négyjegyű szám az 5555.   3. Az $ABCD$ négyszög $AB$ és $CD$ oldala merőleges egymásra. Az $AC$ szakasz felezőpontja $E$, a $BD$ szakaszé $F$. Bizonyítsuk be, hogy ${\overline{AB}}^2+{\overline{CD}}^2=4{\overline{EF}}^2$.  (14 pont)   Megoldás. Legyen a $DC$ és az $AB$ egyenes metszéspontja $O$, és jelölje az $O$ pontból az egyes pontokba mutató vektorokat a megfelelő kisbetű. Tudjuk, hogy $\text{e}=\frac{\text{a}+\text{c}}{2}$ és $\text{f}=\frac{\text{b}+\text{d}}{2}$. Mivel $\overrightarrow{EF}=\text{f}-\text{e}$, így $\begin{array}{c}{\displaystyle 4{\overrightarrow{EF}}^2=4{\left(\text{f}-\text{e}\right)}^2=4{\left(\frac{\text{b}+\text{d}}{2}-\frac{\text{a}+\text{c}}{2}\right)}^2={\left(\text{b}+\text{d}-\text{a}-\text{c}\right)}^2\mathrm{.}}\end{array}$ Mivel $\text{b}\text{d}$, $\text{b}\text{c}$, $\text{a}\text{d}$ és $\text{a}\text{c}$ a merőlegesség miatt 0, így $\begin{array}{c}{\displaystyle {\left(\text{b}+\text{d}-\text{a}-\text{c}\right)}^2={\left(\text{b}-\text{a}\right)}^2+{\left(\text{d}-\text{c}\right)}^2+0={\overrightarrow{AB}}^2+{\overrightarrow{CD}}^2\mathrm{.}}\end{array}$ Azt kaptuk, hogy $4{\overrightarrow{EF}}^2={\overrightarrow{AB}}^2+{\overrightarrow{CD}}^2$, így a bizonyítást befejeztük.   4. Oldjuk meg az alábbi egyenletrendszert: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle x-y}& {\displaystyle =\mathrm{7,}}\hfill \\ \hfill {\displaystyle \sqrt[3]{x^2}+\sqrt[3]{xy}+\sqrt[3]{y^2}}& {\displaystyle =7.}\hfill \end{array}}}\end{array}$  (14 pont)   Megoldás. Használjuk fel, hogy $a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)$, és legyen $a=\sqrt[3]{x}$, $b=\sqrt[3]{y}$. Ekkor $7=a^2+ab+b^2$ és ebből $\begin{array}{c}{\displaystyle 7=a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)=\left(a-b\right)\cdot \mathrm{7,}}\end{array}$ vagyis $a-b=1$ és így $a=b+1$ következik. Ekkor $a^3={\left(b+1\right)}^3=b^3+1+3b\left(b+1\right)$. Az első egyenletből $a^3=7+b^3$. A két egyenlet bal oldala megegyezik, így a jobb oldaluk is egyenlő: $\begin{array}{c}{\displaystyle b^3+1+3b\left(b+1\right)=7+b^3\mathrm{,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle 3b^2+3b-6=\mathrm{0,}{b}^2+b-2=\left(b-1\right)\left(b+2\right)=0.}\end{array}$ Ha $b=\sqrt[3]{y}=1$, akkor $y=1^3=1$, és $x=7+1=8$, ami kielégíti az egyenletrendszert. Ha $b=\sqrt[3]{y}=-2$, akkor $y={\left(-2\right)}^3=-8$ és $x=7-8=-1$, ami szintén jó megoldás.   II. rész     5. Adott egy 14 cm sugarú körlap, melyből kivágunk egy körcikket, amely egy kúp palástja. Mekkora az így kapható legnagyobb térfogatú kúp, és milyen nagy ekkor a körcikk középponti szöge?  (16 pont)   Megoldás. Legyen a körcikk középponti szöge $\alpha \left(\text{rad}\right)$ ($0<\alpha <2\pi$), a hozzá tartozó ív hossza pedig $k_{\alpha }$. Ekkor $\frac{k_{\alpha }}{2\cdot 14\cdot \pi }=\frac{\alpha }{2\pi }$, amiből $k_{\alpha }=14\alpha$. A kúp magassága legyen $m$, alapkörének sugara $R$. Alkotója tudjuk, hogy 14. A kúp alaplapjának kerülete $R\cdot 2\pi =k_{\alpha }$, amiből $\begin{array}{c}{\displaystyle R=\frac{k_{\alpha }}{2\pi }=\frac{14\alpha }{2\pi }=\frac{7\alpha }{\pi }\mathrm{.}}\end{array}$ Felírva a Pitagorasz tételt a kúp magassága, alkotója és alapkörének sugara által alkotott derékszögű háromszögre: $R^2+m^2={14}^2=196$, amiből $\begin{array}{c}{\displaystyle m=\sqrt[]{196-R^2}=\sqrt[]{196-\frac{49{\alpha }^2}{{\pi }^2}}\mathrm{.}}\end{array}$ A kúp térfogata: $\begin{array}{c}{\displaystyle V\left(\alpha \right)=\frac{R^2\pi m}{3}=\frac{\frac{49{\alpha }^2}{{\pi }^2}\cdot \pi \cdot \sqrt[]{196-\frac{49{\alpha }^2}{{\pi }^2}}}{3}=\frac{7^3}{3\pi }{\alpha }^2\sqrt[]{4-\frac{{\alpha }^2}{{\pi }^2}}\mathrm{.}}\end{array}$ $V\left(\alpha \right)$ egy nyílt intervallumon értelmezett függvény, ezért ott lehet szélsőértéke, ahol a deriváltja 0: $\begin{array}{c}{\displaystyle 0=V\text{'}\left(\alpha \right)=\frac{7^3}{3\pi }\left[2\alpha \sqrt[]{4-\frac{{\alpha }^2}{{\pi }^2}}+{\alpha }^2\cdot \frac{-\frac{2\alpha }{{\pi }^2}}{2\sqrt[]{4-\frac{{\alpha }^2}{{\pi }^2}}}\right]\mathrm{.}}\end{array}$ Mivel $\alpha \ne 0$, ezért osztva $\frac{7^3}{3\pi }\cdot \alpha$-val, illetve a gyökös kifejezéssel szorozva a következőt kapjuk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 0}& {\displaystyle =2\left(4-\frac{{\alpha }^2}{{\pi }^2}\right)-\frac{{\alpha }^2}{{\pi }^2}\mathrm{.}}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle =8{\pi }^2-2{\alpha }^2-{\alpha }^2=8{\pi }^2-3{\alpha }^2\mathrm{.}}\hfill \end{array}}$ Ebből (mivel $\alpha >0$) $\begin{array}{c}{\displaystyle \alpha =\sqrt[]{\frac{8}{3}}\pi \mathrm{.}}\end{array}$ Mivel a deriváltfüggvényt pozitív kifejezésekkel osztva és szorozva kaptuk a $8{\pi }^2-3{\alpha }^2$ másodfokú függvényt, így azok előjele adott $\alpha$ esetén megegyezik. A másodfokú függvény menetét figyelembe véve a deriváltfüggvény $\alpha =\sqrt[]{\frac{8}{3}}\pi$ helyen pozitívból negatívba vált, így az az eredeti függvény maximumhelye. A térfogat ekkor $\begin{array}{c}{\displaystyle V=\frac{7^3}{3\pi }\frac{8}{3}\pi \sqrt[]{4-\frac{\frac{8}{3}{\pi }^2}{{\pi }^2}}=\frac{7^3\cdot 8}{9}\pi \sqrt[]{\frac{4}{3}}\approx 1106\mathrm{,}0145.}\end{array}$   6. A kosárlabda mérkőzéseken a büntetődobások szabálya a következő: a büntetőt végző játékos kétszer vagy háromszor dobhat, minden kosárral $1$ pontot szerezhet, összesen legföljebb $2$-t. Egy kosaras $p>0$ valószínűsséggel dob be egy büntetőt. $a)$ Milyen $p$ valószínűség esetén szerez a játékos ugyanakkora eséllyel $1$, illetve $2$ pontot? $b)$ Írjuk föl tetszőleges $p$ valószínűség mellett a büntetődobásokkal szerzett pontok várható értékét.  (16 pont)   Megoldás. Jelölje az $X$ változó azt, hogy a játékos hány pontot szerez. $a)$ 1 pontot úgy kaphat, ha a három dobásból kettőt kihagy, egyet bedob. Erre nyilván három lehetősége van, tehát $P\left(X=1\right)=3{\left(1-p\right)}^{2}p$. Két pontot vagy úgy kaphat, hogy az első vagy a második dobást kihagyja, a többit bedobja, vagy pedig az első kettőt bedobja (és ekkor többet nem dob). Tehát $P\left(X=2\right)=2p^2\left(1-p\right)+p^2=p^2\left(3-2p\right)$. Ha a kettő egyenlő, akkor: $\begin{array}{c}{\displaystyle 3{\left(1-p\right)}^{2}p=p^2\left(3-2p\right)\mathrm{.}}\end{array}$ Mivel $p\ne 0$, ezért oszthatunk vele, majd felbontjuk a zárójeleket: ${\displaystyle \begin{array}{c}\hfill {\displaystyle 3\left(1-2p+p^2\right)=p\left(3-2p\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle 0=5p^2-9p+\mathrm{3,}}\hfill \\ \hfill {\displaystyle p=\frac{9\pm \sqrt[]{81-60}}{10}=\frac{9\pm \sqrt[]{21}}{10}\mathrm{.}}\hfill \end{array}}$ Ebből a nagyobbik gyök $1$-nél nagyobb, tehát az egyetlen megoldás a $p=\frac{9-\sqrt[]{21}}{10}\approx 0\mathrm{,}4417$. $b)$ Felhasználva az $a)$ pontban kapott értékeket: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle E\left(X\right)}& {\displaystyle =2\cdot p^2\left(3-2p\right)+1\cdot 3{\left(1-p\right)}^{2}p+0\cdot P\left(X=0\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =6p^2-4p^3+3p-6p^2+3p^3=-p^3+3p\mathrm{.}}\hfill \end{array}}$   7. A lakásunk fűtését biztosító gázkazán elavult, sokszor javításra szorul, melynek költsége évente 15 000 Ft. Egy új kazán, amely hosszú ideig nem szorul javításra, 400 000 Ft-ért kapható. Érdemes volna új készüléket vásárolni. Erre két lehetőségünk van. Az egyik, hogy megtartjuk a régi készüléket, takarékoskodunk, és csak akkor veszünk újat a jelenlegi áron (megfigyelésünk szerint minden évben kapható hasonló készülék ilyen áron), amikor összejön rá a pénz. A banknál havi 10 000 Ft befizetésével egy külön takarékszámlán gyűjtjük a pénzt, amelyre éves $2\%$ kamatot kapunk, amit havonta jóváírnak. Ebben az esetben azonnal megvásároljuk a készüléket, amint a pénz rendelkezésre áll, de sajnos minden megkezdett évben ki kell fizetnünk a javítás költségét. A másik lehetőség, hogy folyószámlahitelből megvesszük a készüléket. Ennek éves kamata $20\mathrm{,}41\%$. A családi költségvetésből a kölcsön törlesztésére évi 135 000 Ft-ot tudunk szánni. Melyik a számunkra pénzügyileg kedvezőbb eset?  (16 pont)   Megoldás. Ha félretesszük a pénzt, akkor $n$ hónap után akkor tudjuk megvásárolni a készüléket, amikor a $400000\le \frac{q^{n+1}-1}{q-1}\cdot 10000$ egyenlőtlenség teljesül, ahol $q=\sqrt[12]{1\mathrm{,}02}$. Az egyenlőtlenség mindkét oldalát 10 000-rel osztva, majd rendezve ($q-1>0$, tehát nem fordul meg a relációsjel): ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 40\left(q-1\right)}& {\displaystyle \le q^{n+1}-\mathrm{1,}}\hfill \\ \hfill {\displaystyle 40q-39}& {\displaystyle \le q^{n+1}\mathrm{.}}\hfill \end{array}}$ Mivel $q>1$, ezért az $x\mapsto \text{log}{}_{q}x$ függvény szigorúan monoton növekedő. Azaz ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{log}{}_q\left(40q-39\right)}& {\displaystyle \le n+\mathrm{1,}}\hfill \\ \hfill {\displaystyle \frac{\text{ln}\left(40q-39\right)}{\text{ln}q}-1}& {\displaystyle \le n\mathrm{,}}\hfill \\ \hfill {\displaystyle 37\mathrm{,}766}& {\displaystyle \le n\mathrm{,}}\hfill \end{array}}$ vagyis 38 havi befizetésre van szükség, ami összesen 380 000 Ft, a régi készülék karbantartási költségével együtt legfeljebb 440 000 Ft. Ha kölcsönt veszünk fel, akkor évente 135 000 Ft-ot fizetünk be. Ha a 400 000 Ft-ot $k$ év alatt kifizetjük, akkor a következő egyenlőtlenség teljesül: $\begin{array}{c}{\displaystyle 400000\cdot 1\mathrm{,}{2041}^k\le 135000\cdot \frac{1\mathrm{,}{2041}^k-1}{\mathrm{0,2041}}\mathrm{.}}\end{array}$ Osztva 1000-rel és rendezve: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 400\cdot 1\mathrm{,}{2041}^k}& {\displaystyle \le 661\mathrm{,}4405\cdot \left(1\mathrm{,}{2041}^k-1\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle 661\mathrm{,}4405}& {\displaystyle \le 261\mathrm{,}4405\cdot 1\mathrm{,}{2041}^k\mathrm{,}}\hfill \\ \hfill {\displaystyle 2\mathrm{,}529985}& {\displaystyle \le 1\mathrm{,}{2041}^k\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{\text{ln}2\mathrm{,}529985}{\text{ln}1\mathrm{,}2041}}& {\displaystyle \le k\mathrm{,}}\hfill \\ \hfill {\displaystyle 4\mathrm{,}9976}& {\displaystyle \le k\mathrm{.}}\hfill \end{array}}$ Tehát 5 évig kell fizetni a kölcsönt, ami összesen $5\cdot 135000=675000$ Ft, ami jóval több a 440 000-nél.     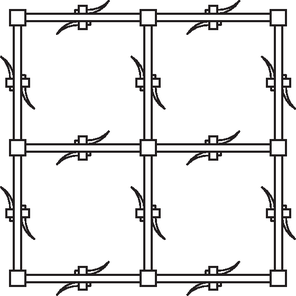8. A mellékelt ábra egy vas kerítés négy ismétlődő elemét mutatja oldalnézetből. A hosszú elemek mérete 30 cm és 4 cm, az őket egymáshoz kapcsoló négyzetek oldala 8 cm. Az íves elemeket kapcsoló négyzetek oldala 4 cm, a mellettük megtalálható négyzet oldala 2 cm. Az íves elemek merőlegesen csatlakoznak a 4 cm oldalú négyzethez és két körív határolja őket, melyek középpontja a négyzet csatlakozó oldalélének meghosszabbításán van. A kisebb kör sugara 12 cm, a hozzá tartozó ív a 4 cm-es négyzet csúcsánál indul és ${60}^{\circ }$-os középponti szögű. A nagyobb sugarú körív a négyzet oldalának középpontjánál kezdődik. A kerítés teljes vasszerkezete 2 cm vastagságú, függőlegesen négy, vízszintesen huszonnégy ismétlődő elemből áll.     $a)$ Számítsuk ki az íves elemet létrehozó nagyobb sugarú kör sugarát és a hozzá tartozó ív középponti szögét. $b)$ Számítsuk ki az íves elemek oldalnézetből látható területét. $c)$ Hány kg vasra volt szükség a kerítéshez? 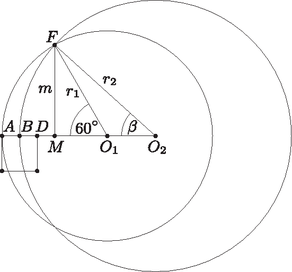(A vas sűrűsége $7\mathrm{,}86\frac{\text{g}}{{\text{cm}}^3}$.)  (16 pont)   Megoldás. Használjuk az ábra jelöléseit. Tudjuk, hogy $r_1=12$, $AB=BD=2$. Mivel $F{O}_{1}M={60}^{\circ }$, ezért $m=6\sqrt[]{3}$ és $M{O}_1=6$. Ez utóbbiból $\begin{array}{c}{\displaystyle DM=A{O}_1-AD-M{O}_1=r_1-4-6=2}\end{array}$ következik.     $a)$ Tudjuk, hogy ${\displaystyle \begin{array}{cc}\hfill {\displaystyle r_2}& {\displaystyle =B{O}_2=BD+DM+M{O}_1+O_1{O}_2=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =2+2+6+O_1{O}_2\mathrm{,}}\hfill \end{array}}$ amiből $O_1{O}_2=r_2-10$. Írjuk fel a Pitagorasz-tételt az $FM{O}_2$ háromszögre: ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left(6\sqrt[]{3}\right)}^2+{\left(6+O_1{O}_2\right)}^2=r_2^2\mathrm{,}}\hfill \\ \hfill {\displaystyle 36\cdot 3+{\left(r_2-4\right)}^2=r_2^2\mathrm{,}}\hfill \\ \hfill {\displaystyle 124=8r_2\mathrm{,}{r}_2=15\mathrm{,}5\text{cm}\mathrm{.}}\hfill \end{array}}$ Ebből pedig (felhasználva, hogy $\beta$ hegyesszög) $\begin{array}{c}{\displaystyle \beta =\text{arcsin}\frac{m}{r_2}=\text{arcsin}\frac{6\sqrt[]{3}}{15\mathrm{,}5}\approx 42\mathrm{,}{10}^{\circ }\mathrm{.}}\end{array}$ $b)$ Az $O_1$ középpontú, $r_1$ sugarú, ${60}^{\circ }$-os középponti szögű körcikk területét $t_1$-gyel, az $O_2$ középpontú, $r_2$ sugarú és $\beta$ középponti szögű körcikk területét pedig $t_2$ vel jelölve egy íves elem területe: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T}& {\displaystyle =\left[t_1-t_{FM{O}_1▵}\right]-\left[t_2-t_{FM{O}_2▵}\right]=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left[\frac{60}{360}\cdot {12}^2\pi -\frac{6\sqrt[]{3}\cdot 6}{2}\right]-\left[\frac{42\mathrm{,}10}{360}\cdot 15\mathrm{,}{5}^2\pi -\frac{6\sqrt[]{3}\left(15\mathrm{,}5-4\right)}{2}\right]\approx 15\mathrm{,}71{\text{cm}}^2\mathrm{.}}\hfill \end{array}}$ $c)$ Egy hosszú elem és a hozzá csatlakozó két íves elem és négy négyzet területe együtt $2\cdot \left(15\mathrm{,}71+2\cdot 2+4\cdot 4\right)+30\cdot 4=191\mathrm{,}42{\text{cm}}^2$. Mivel ebből összesen $24\cdot \left(4+1\right)+4\cdot \left(24+1\right)=220$ darab van, ez együtt $220\cdot 191\mathrm{,}42=42112\mathrm{,}4{\text{cm}}^2$. A hosszú elemeket összekapcsoló négyzetek összes területe $\begin{array}{c}{\displaystyle \left(4+1\right)\left(24+1\right)\cdot 8\cdot 8=8000{\text{cm}}^2\mathrm{,}}\end{array}$ a kerítés teljes területe oldalnézetből $42112\mathrm{,}4+8000=50112\mathrm{,}4{\text{cm}}^2$. A kerítés térfogata tehát $2\cdot 50112\mathrm{,}4=100\mathrm{224,8}{\text{cm}}^3$. 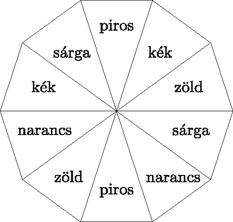Mivel a vas sűrűsége $7\mathrm{,}86\frac{\text{g}}{{\text{cm}}^3}$, így a kerítés vasszerkezetének tömege $\begin{array}{c}{\displaystyle 100224\mathrm{,}8\cdot 7\mathrm{,}86=787766\mathrm{,}928\text{g}\approx 787\mathrm{,}77\text{kg}\mathrm{.}}\end{array}$   9. Egy társasjáték szabályos tízszög alakú tábláját a következő módon szeretnénk kiszínezni: öt szín (piros, kék, zöld, sárga, narancs) mindegyikét kétszer felhasználva a tíz cikket úgy színezzük ki, hogy mindegyik színpár pontosan egy esetben legyen egymással szomszédos cikk színe. Az ábrán egy jó színezés látható. (A tábla díszített, ezért az elforgatásokkal és tükrözésekkel kapott színezések különböznek egymástól.)     $a)$ Ha öt szomszédos cikket már kiszíneztünk öt különböző színnel, akkor a többit ‐ szintén minden színt egyszer felhasználva ‐ hányféleképpen színezhetjük ki? $b)$ Adjunk példát olyan színezésre, ahol nincs egymás mellett öt különböző színű cikk.  (16 pont)   Megoldás. A színeket az egyszerűség kedvéért jelöljük az 1-től 5-ig terjedő egész számokkal. Egy cikket kitüntetve, majd az óramutató járását követve írjuk le a színezést. Az ábrán látható színezés pl. (1234513524). $a)$ A színezés a következő: (12345xxxxx). Az 1-es mellé 3, 4 vagy 5 kerülhet. I. eset: a 3-as kerül oda, ekkor a színezés így alakul: (12345xxxx3). A 3 mellett csak 5 állhat, az 5 mellett pedig 1 vagy 2. A másik 5 mellett is 1 vagy 2 állhat, az utolsó szabad helyen pedig 4. Vagyis két ilyen színezés van: (1234524153) vagy (1234514253). II. eset: a 4-es kerül oda. A 4 mellé csak 2 kerülhet, a 2 mellé csak 5. Az 5 mellé 1 vagy 3. A másik 4 mellé 5 kerül, a maradék helyre pedig 3 vagy 1. A két lehetőség, amit kaptunk: (1234531524) vagy (1234513524). III. eset: az 5 kerül oda, mellé a 2 vagy a 3 mehet. Ha 2, akkor ezt az esetet kapjuk: (1234524135). Ha 3, akkor ezt: (1234531425). Ez összesen 6 lehetőség. $b)$ Az $a)$ részben használt jelöléssel egy megfelelő színezés: (1231534524).