Kezdőlap


Cím:	Megoldásvázlatok a 2015/8. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Székely Péter
Füzet:	2015/december, 525 - 533. oldal	PDF \| MathML
Témakör(ök):	Felvételi előkészítő feladatsor

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. rész

1. Milyen

α

valós paraméter esetén lesz a következő egyenletnek egy megoldása?

\begin{matrix} \frac{x^{2} cos α + x + \frac{1}{2} sin α}{x^{2} - \frac{1}{2}} = 0. \end{matrix}

(11 pont)

Megoldás. A nevezőben nem állhat nulla, tehát

x \neq \pm \frac{\sqrt[]{2}}{2}

. Egy tört akkor lehet nulla, ha a számlálója nulla, vagyis

\begin{matrix} x^{2} cos α + x + \frac{1}{2} sin α = 0. \end{matrix}

Ennek a másodfokú egyenletnek akkor lesz pontosan egy megoldása, ha

a)

Nem másodfokú az egyenlet, vagyis a másodfokú tag együtthatója nulla. Ekkor

cos α = 0

, azaz

\begin{matrix} α = \frac{π}{2} + k π (ahol k \in Z) . \end{matrix}

Ekkor

\begin{matrix} x + \frac{1}{2} sin α = 0, \end{matrix}

melyre

\begin{matrix} \begin{matrix} α_{1} & = \frac{π}{2} + 2 k π & esetén & x_{1} & = - \frac{1}{2}, \\ α_{2} & = \frac{3 π}{2} + 2 k π & esetén & x_{2} & = \frac{1}{2} . \end{matrix} \end{matrix}

b)

Másodfokú az egyenlet (

cos α \neq 0

), s ekkor az egyenlet diszkriminánsa nulla. Ebből

\begin{matrix} 1 - 4 \cdot cos α \cdot \frac{1}{2} sin α = 0, \end{matrix}

vagyis

sin 2 α = 1

adódik. Ennek gyökei

α = \frac{π}{4} + l π

, ahol

l \in Z

. A paraméter ezen értékei azonban nem felelnek meg a feltételeknek, hiszen

α = \frac{π}{4}

esetén

x = - \frac{\sqrt[]{2}}{2}

α = \frac{5 π}{4}

esetén

x = \frac{\sqrt[]{2}}{2}

adódik.
Tehát az egyenletnek csak

α = \frac{π}{2} + k π

esetén lesz egy valós gyöke.

2. Óvodás korú kisöcsénk a játék rulett-zsetonokat használja toronyépítésre. Az első korongoszlop mellé magasabbat állít, majd a következőket ugyanannyival növeli, mint a korábbiakat. Így egy lépcsős toronysorozatot hoz létre mackójának.

a)

Milyen sorozatot alkotnak a tornyok magasságai?

b)

Az első toronytól kezdve csoportosítsuk a tornyokat hármasával. Igazoljuk, hogy a hármas csoportokban szereplő tornyok magasságainak összege számtani sorozatot alkot.

c)

A sorba rendezett tornyok elejéről kisöcsénk elvett

n

darab tornyot, majd megszámoltatta velünk, hogy hány zsetonja van összesen. Ezután elvett még

n

Megoldás.

a)

Mivel a szomszédos tornyok magasságai ugyanannyival növekednek, ezért számtani sorozatot alkotnak. (Ez a számtani sorozat definíciója.)

b)

Jelölje az

a)

-beli sorozat általános tagját

a_{n}

, differenciáját pedig

d

. Ekkor az új sorozat egy általános elemét így írhatjuk fel:

\begin{matrix} b_{n} & = a_{3 n - 2} + a_{3 n - 1} + a_{3 n} = 3 \cdot a_{3 n} - 3 d = 3 a_{1} - 6 d + n \cdot 9 d . \end{matrix}

Ebből kiolvasható a számtani sorozat definíciója, a

9 d

-s állandó növekedés. Vagy igazolhatjuk az állítást a

\begin{matrix} 2 b_{n} = b_{n - 1} + b_{n + 1}, 2 (3 \cdot a_{3 n} - 3 d) = (3 a_{3 n} - 12 d) + (3 a_{3 n} + 6 d) \end{matrix}

összefüggéssel is.

c)

Legyen

\begin{matrix} s_{n} & = b = \frac{2 a_{1} + (n - 1) d}{2} \cdot n = a_{1} n + \frac{(n - 1) n d}{2}, \\ s_{2 n} & = c = \frac{2 a_{1} + (2 n - 1) d}{2} \cdot 2 n = 2 a_{1} n + \frac{(2 n - 1) 2 n d}{2}, \\ s_{3 n} & = \frac{2 a_{1} + (3 n - 1) d}{2} \cdot 3 n = \frac{6 a_{1} n + (3 n - 1) 3 n d}{2} = 3 a_{1} n + \frac{9 n \cdot n d}{2} - \frac{3 n d}{2} . \end{matrix}

Ekkor

\begin{matrix} c - b = a_{1} n + \frac{3 n \cdot n d}{2} - \frac{n d}{2}, \end{matrix}

amiről látható, hogy éppen az

s_{3 n}

harmada. Tehát

s_{3 n} = 3 (c - b)

3. Az

A

halmaz elemei olyan

100

-nál kisebb pozitív

a

egészek, melyekre

sin (a \cdot 10^{\circ}) = 0, 5

. A

B

halmaz elemei a

100

-nál kisebb hattal osztható természetes számok.

a)

| A | = ? | B | = ?

b)

Definiáljuk a

C

halmazt a következőképpen:

C : = {1; 2; 3; 6; A}

, ahol az

A

halmaz a

C

eleme.

| C ∖ B | = ?

c)

Hány páros elemű részhalmaza van

C

-nek? (14 pont)

Megoldás.

a)

sin (a \cdot 10^{\circ}) = 0, 5

egyenlet megoldásai

\begin{matrix} a \cdot 10^{\circ} = 30^{\circ} + k \cdot 360^{\circ}, illetve a \cdot 10^{\circ} = 150^{\circ} + l \cdot 360^{\circ}, \end{matrix}

melyekből a 100-nál kisebb

a

értékek a 3, 39, 75, illetve 15, 51, 87. Tehát

| A | = 6

.
A

B

halmaz elemei:

0,6,12, ...,96

. Tehát

| B | = 17

b)

C ∖ B = {1; 2; 3; A}

, tehát

| C ∖ B | = 4

c)

Az öt elemű

C

halmaznak a páros elemű részhalmazai a 0, 2, illetve 4 eleműek. Ezekből rendre

(\binom{5}{0})

(\binom{5}{2})

(\binom{5}{4})

van, ami összesen

1 + 10 + 5 = 16

darab.

4. A Balaton valósághű modelljét szeretnénk elkészíteni. Az adatok szerint a Balaton hossza 77 km, felszíne

594 {km}^{2}

, átlagos mélysége 3,6 m, legmélyebb pontja 11 m.

a)

Hány centiméter mélyen lesz a modellünk legmélyebb pontja a felszínhez képest, ha annak hossza a terepasztalon 1 m?

b)

Mennyi a modellünk léptéke (méretaránya)?

c)

Hány centiliter víz kell a modellhez, ha azt valóban vízzel szeretnénk feltölteni?

d)

A Balatont egy helikopterről fentről is megtekintjük, hogy lássuk, mennyire hasonlít a modellünkre. A tó két legtávolabbi, egymástól 77 km-re lévő pontját nézzük hossztengelyére merőlegesen, középpontja felé repülve. 4 km távolságban, 900 m magasról mekkora szögben látjuk a tavat? (14 pont)

Megoldás.

a)

A megfelelő hosszúságok arányát felírva

\begin{matrix} \frac{h}{11 m} = \frac{1 m}{77 km} = \frac{1 m}{77 000 m}, amiből h = \frac{11 m}{77 000} \approx 0, 0143 cm adódik. \end{matrix}

b)

Az előző részben felírt megfelelő hosszúságok aránya a hasonlóság aránya:

λ = \frac{1}{77 000}

. Tehát a lépték

1 : 77 000

c)

A Balatonban

V = 594 \cdot 10^{6} \cdot 3, 6 (m^{3})

víz van. A modellben

V' = λ^{3} \cdot V \approx 0, 468 cl

víz van.

d)

Legyen a Balaton két legtávolabbi pontja

A

és

B

, a közepe

F

. Az

A B

szakaszra merőlegesen érkező helikopter a 0,9 km magasan lévő

H

pontból nézi az

A B

távolságot, a

H

pont merőleges vetülete a Balaton síkjára

H^{⊥}

. A feladat az

A H B ∢

szög meghatározása.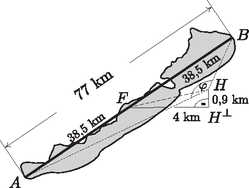

F H H^{⊥} ▵

derékszögű, így

\begin{matrix} \bar{F H} = \sqrt[]{4^{2} + 0, 9^{2}} = 4, 1 km. \end{matrix}

F H ⊥ F B

, és így

tg \frac{φ}{2} = \frac{F B}{F H}

, tehát

φ \approx 167, 84^{\circ}

II. rész

5. Egy bank a következő ajánlattal kívánja ügyfelei körét bővíteni: aki a megadott határidőig pénzét áthozza a fiókba fél éves lekötéssel, az első hat hónapban évi

5 %

kamatot kap. Az apró betűs részt elolvasva megtudhatjuk, hogy fél év után havi lekötéssel, évi 1,5% kamattal marad a fiókban a pénzünk. (A havi lekötés azt jelenti, hogy amennyiben előbb vesszük ki a pénzünket, a teljes kamatot elveszítjük a csonka hónapra.)

1

millió forintot teszünk be a bankba. Ezen feltételek ismeretében válaszoljunk a következő kérdésekre:

a)

Mennyi pénzünk lesz fél év múlva?

b)

Mennyit kamatozott egy év alatt a betett

1

millió forintunk?

c)

Korábbi bankfiókunkban hagyva a pénzünket évi

2 %

-os a kamatot kapnánk havi lekötés mellett. Legfeljebb mennyi időre éri meg áthozni a pénzünket az új helyre? (16 pont)

Megoldás.

a)

Fél év alatt 5% kamattal kell számolni, de nem a teljes évre, csupán feleannyi időre. Így

1 000 000 \cdot {(1 + 0, 05)}^{\frac{1}{2}}

, vagyis egészre kerekítve 1 024 695 Ft-unk lesz.

b)

A teljes évre a kamat:

\begin{matrix} {(1 + 0, 05)}^{\frac{1}{2}} \cdot {(1 + 0, 015)}^{\frac{1}{2}} \approx 1, 032 4, \end{matrix}

tehát kb. 3,24% a kamat a teljes évre.
(A második félévben már csak 1,5% volt a kamat, így

1 024 695 \cdot {(1, 015)}^{\frac{1}{2}} \approx 1 032 352

forintunk lett.)

b)

A feladat megállapítani, hogy hány évre érdemes áthozni a pénzünket a feltételeknek megfelelően. (Feltételezzük, hogy a két bank egyéb költségei nem különböznek, és így csak a hűségidőn múlik, hogy érdemes-e átmenni egyik bankból a másikba.)

\begin{matrix} 1 000 000 \cdot 1, 02^{n} & = 1 000 000 \cdot 1, 05^{\frac{1}{2}} \cdot 1, 015^{n - \frac{1}{2}}, \\ {(\frac{1, 02}{1, 015})}^{n} & = {(\frac{1, 05}{1, 015})}^{\frac{1}{2}}, \\ n & = \frac{\frac{1}{2} ln (\frac{1, 05}{1, 015})}{ln (\frac{1, 02}{1, 015})} \approx 3, 45. \end{matrix}

Tehát kb. három és fél évnél kevesebb időtartam esetén megéri áthozni a pénzt az új feltételeknek megfelelően. (Vagyis hosszabb időre nem éri meg áthozni a pénzünket.)

6. Ugorjunk másfél évet. Az egyetemek új előírása miatt a

2017

-es érettségin igen sokan választották a matematikát emelt szinten.

10 %

-uknak

90 %

feletti lett az eredménye.

a)

Az emelt szinten érettségiző diákok közül véletlenszerűen megkérdezve

10

-et mekkora annak az esélye, hogy közülük pontosan ketten

90 %

feletti érettségit tettek?

b)

Internetes felmérésen

100

diákot kérdeztek meg véletlenszerűen az emelt szinten érettségizők közül. Mekkora a valószínűsége, hogy legfeljebb

2

-en vizsgáztak

90 %

feletti eredménnyel? És annak, hogy a

100

megkérdezett diákból legfeljebb ketten vannak azok, akiknek nem sikerült

90 %

felett az eredményük?

c)

(Az emelt szinten túlmutató kérdés.) Az OH statisztikájában kutakodunk. A

40 000

emelt szintű vizsgázó eredményét tekintve

90 %

-os biztonsággal hány

90 %

feletti eredményes vizsgázóra számíthatunk? (16 pont)

Megoldás.

a)

Az érettségizők nagy száma miatt binomiális eloszlással számolhatunk. A visszatevéses urna-modell szerint 0,1 valószínűséggel választhatjuk ki a 90% feletti tanulókat, s a maradék nyolcat 0,9 valószínűséggel. Ezen tanulókat pedig

(\binom{10}{2})

-féleképpen választhatjuk ki. Eszerint

\begin{matrix} P (X = 2) = (\binom{10}{2}) \cdot 0, 9^{8} \cdot 0, 1^{2} \approx 0, 1937. \end{matrix}

Tehát kb. 19,37% annak az esélye, hogy pontosan két 90% feletti eredményű tanulót találunk az adathalmazban.

(A grafikonról jól látszik, hogy a legnagyobb esélye annak lenne, hogy egy tanulót találunk, aki a feltételnek megfelel.)

b)

Annak az esélye, hogy legfeljebb két 90% feletti eredményt nyújtó diákot találjunk, azzal egyezik meg, hogy pontosan kettő, vagy pontosan egy, illetve egy ilyen diákot sem találunk a 10 tanuló között.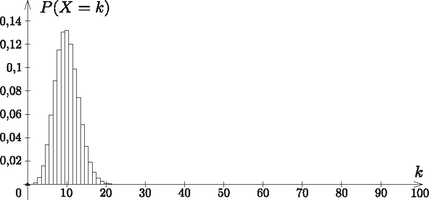

\begin{matrix} P (X \leq 2) & = P (X = 0) + P (X = 1) + P (X = 2) = \sum_{i = 0}^{2} (\binom{100}{i}) \cdot 0, 9^{100 - i} \cdot 0, 1^{i} \approx \\ \approx 0, 000 027 + 0, 000 295 + 0, 001 623 = 0, 001 945. \end{matrix}

Tehát annak az esélye, hogy legfeljebb két 90% feletti eredményt író tanulót találunk, kb. 0,19%, közel nulla. (Ez a lenti grafikonon is jól leolvasható, a görbe bal széle.)

Annak az esélye, hogy legfeljebb két olyan diákot találjunk, akiknek nem sikerült 90% felett az érettségijük, megegyezik azzal, hogy 0, 1 vagy 2 ilyen diák van.

\begin{matrix} P (Y \leq 2) = P (Y = 0) + P (Y = 1) + P (Y = 2) = \sum_{i = 0}^{2} (\binom{100}{i}) \cdot 0, 1^{100 - i} \cdot 0, 9^{i} \approx 0. \end{matrix}

c)

A feladat szerint nem szeretnénk nagyon hibázni, 90% biztonsággal akarjuk meghatározni azon vizsgázók számát, akik 90%-nál jobban teljesítettek. A kérdés tehát az, hogy legfeljebb hány ilyen tanulóra számíthatunk 90%-os biztonsággal.
Az előző grafikonokból is jól látszik, hogy eszerint azt az

n

értéket keressük, melynél kisebb

n

-ekre az oszlopok területe a teljes grafikon területének 90%-a lesz. Ez a számítás binomiális eloszlással legfeljebb számítógép segítségével (pl. GeoGebra ‐ ld. a GEOMATECH

^{1}

oldalán lévő statisztikai feladatokat) lenne elvégezhető, így közelítsük eloszlásunkat normális eloszlással.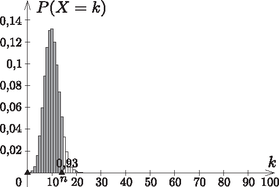

Az eloszlás várható értéke

E (X) = 0, 1 \cdot 40 000 = 4 000

, szórása

\begin{matrix} D (X) = \sqrt[]{0, 1 \cdot 0, 9 \cdot 40 000} = 60. \end{matrix}

A normális¹ eloszláshoz a görbénket transzformálnunk kell, hogy a jól ismert Gauss-görbét megkapjuk

(f (x) = \frac{1}{\sqrt[]{2 π}} e^{- \frac{x^{2}}{2}})

:
1. toljuk el a maximumát az

y

-tengelyhez (

E (X)

-szel való eltolás);
2. alakítsuk úgy át, hogy területe 1 legyen (osszuk

D (X)

-szel ,,belül'', hogy merőleges affinitást hajtsunk végre az

x

-tengely irányában).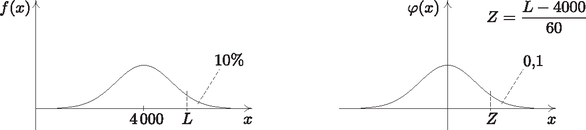

Ekkor a görbe alatti integrálás lenne a feladatunk, de ,,szerencsére'' a függvénytáblázat

Φ (Z)

-táblázatát használva visszakereshetjük, hogy milyen

x

abszcisszáig integrálva lenne a görbe alatti terület 0,9:

\begin{matrix} P (X \leq L) = Φ (\frac{L - 4000}{60}) = 0, 9, \frac{L - 4000}{60} = 1, 28, L = 4076, 8. \end{matrix}

Tehát elegendő legfeljebb 4 077 tanulót mondani, hogy 90% biztonsággal eltaláljuk, hogy hányan írták meg 90%-nál jobban a dolgozatot.

7. Adott a valós számok halmazán értelmezett

f

függvény:

\begin{matrix} f : x \mapsto \frac{x}{1 - | x |} . \end{matrix}

a)

Ábrázoljuk a függvényt a

] - 1; 2] ∖ {1}

intervallumon.

b)

Adott a

g (x) = 2 x

függvény. Mi lesz az

f \circ g

függvény értékkészlete a

] - 1; 2]

intervallumon?

c)

Határozzuk meg az

f

függvény inverzét a

] - 1; 1 [

intervallumon, s ábrázoljuk az

f^{- 1}

függvényt. (16 pont)

Megoldás.

a)

A függvény ábrázolásához bontsuk fel az abszolútértéket:

\begin{matrix} f : x \mapsto {\begin{matrix} \frac{x}{1 - (- x)} = \frac{x}{1 + x} = \frac{x + 1}{x + 1} + \frac{- 1}{x + 1} = \frac{- 1}{x + 1} + 1, & ha x < 0, x \neq - 1, \\ \frac{x}{1 - x} = - \frac{x - 1 + 1}{x - 1} = \frac{- 1}{x - 1} - 1, & ha x \geq 0, x \neq 1. \end{matrix} \end{matrix}

Ezekről az alakokról jól leolvashatók a függvénytranszformációk. A megfelelő intervallumokon ábrázoljuk a függvényeket (1. ábra).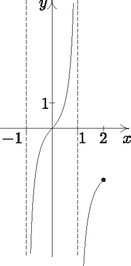

1. ábra

b)

f (x) \to f (2 x)

függvénytranszformáció egy

x

tengely irányú merőleges affinitásnak felel meg (

x

tengely irányában történő zsugorítás, 2. ábra).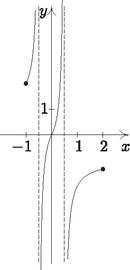

2. ábra

Természetesen ezt is meggondolhatjuk az abszolútérték bontásának segítségével:

\begin{matrix} f : x \mapsto {\begin{matrix} \frac{2 x}{1 - (- 2 x)} = \frac{x}{\frac{1}{2} + x} = \frac{- \frac{1}{2}}{x + \frac{1}{2}} + 1, & ha x < 0, x \neq - \frac{1}{2}, \\ \frac{2 x}{1 - 2 x} = \frac{- \frac{1}{2}}{x - \frac{1}{2}} - 1, & ha x \geq 0, x \neq \frac{1}{2} . \end{matrix} \end{matrix}

Ábrázolás nélkül is, az előzőek alapján, látható, hogy a függvény értékkészlete a teljes valós számhalmaz.

c)

A függvény a

] - 1; 1 [

intervallumon kölcsönösen egyértelmű hozzárendelés, így invertálható.

x < 0

esetén:

\begin{matrix} y = \frac{x}{1 + x} \to_{}^{x \leftrightarrow y} x = \frac{y}{1 + y} \to y = \frac{- 1}{x - 1} - 1. \end{matrix}

x \geq 0

esetén:

\begin{matrix} y = \frac{x}{1 - x} \to_{}^{x \leftrightarrow y} x = \frac{y}{1 - y} \to y = \frac{- 1}{x + 1} + 1. \end{matrix}

A vastagon ábrázolt rész a kért

] - 1; 1 [

intervallumon értelmezett függvény.

8. Lakásunk nappali szobája hatszög alakú, melynek oldalai rendre

A B = 3, 4

B C = 2, 3

C D = 2, 3

D E = 2, 3

E F = 3, 4

, valamint

F A = 3, 7

méteresek. Az

A B

és a

B C

, valamint a

D E

és az

E F

oldalak merőlegesek egymásra. A szoba parkettázásához szeretnénk megállapítani az alapterületét, melyet kétféleképpen teszünk meg.
Mi megmérjük a szoba

A D

átlóját, melyet

4, 8

méteresnek találunk, míg fiaink a szoba

F

csúcsánál lévő szöget határozzák meg, melyet

120^{\circ}

-nak mérnek. A hosszúságot 5 cm-es pontossággal, míg a szöget

5^{\circ}

-os pontossággal tudjuk eszközeinkkel megmondani.

a)

A szög vagy a hosszúság relatív hibája nagyobb?

b)

Mekkorák a területek a két esetben?

c)

Mennyire pontosan ismerjük a két esetben az

A D

átlót?

d)

Melyik mérést fogadjuk el inkább? (16 pont)

Megoldás.

a)

Tudjuk, hogy a hosszúság abszolút hibája:

H (\bar{A B}) = 0, 05

m. A relatív hibája:

R (\bar{A B}) = \frac{0, 05}{4,8} \approx 0, 01

, vagyis közelítőleg 1%. A szög esetén:

H (A F E ∢) = 5^{\circ}

R (A F E ∢) = \frac{5}{120} \approx 0, 04

, ami 4%. Tehát a szög relatív hibája a nagyobb.

b)

Készítsük el a szoba vázlatrajzát. Az ábrán látható

c

oldalt Pitagorasz-tétel segítségével számíthatjuk ki: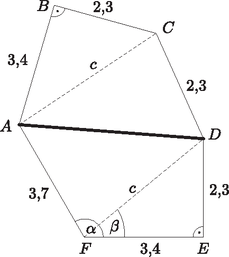

\begin{matrix} c = \sqrt[]{2, 3^{2} + 3, 4^{2}} \approx 4, 1. \end{matrix}

Az első esetben a

A B C

és

D E F

háromszögek területét két befogójuk segítségével, míg a két belső háromszög területét Heron-képlet segítségével határozhatjuk meg:

\begin{matrix} T & = & 2 \cdot \frac{2, 3 \cdot 3, 4}{2} + \sqrt[]{5, 6 \cdot 0, 8 \cdot 3, 3 \cdot 1, 5} + \\ + \sqrt[]{6, 3 \cdot 2, 6 \cdot 2, 2 \cdot 1, 5} \approx 19, 88 m^{2} . \end{matrix}

A második esetben az

α

szög segítségével határozzuk meg

A D

hosszúságát (koszinusz-tétel). Az

F E D

háromszögben

tg β = \frac{2,3}{3,4}

, amiből

β \approx 34, 08^{\circ}

\begin{matrix} A D = \sqrt[]{3, 7^{2} + c^{2} - 2 \cdot 3, 7 \cdot c \cdot cos (α - β)} \approx 5, 33. \end{matrix}

Ezután a területeket hasonlóképpen határozhatjuk meg:

\begin{matrix} T' = 2 \cdot \frac{2, 3 \cdot 3, 4}{2} + \sqrt[]{5, 1 \cdot 1, 27 \cdot 2, 8 \cdot 1} + \sqrt[]{8, 815 \cdot 1, 715 \cdot 2, 115 \cdot 1, 985} \approx 18, 38 m^{2} . \end{matrix}

c)

A hosszmérést

\pm 5

cm hibával végezhetjük, ezért

475 cm < A D < 485 cm

, a szöggel való számolásnál 530 cm-t kaptunk, tehát biztosan sokkal pontatlanabb ez az adat.

d)

A két esetben ‐ a hibaszámítás tekintetében ‐ azonos műveletsorozatokat hajtunk végre az

A D

átlón, így a második esetben nagyobb hibával ismerjük a területet, mint az elsőben.

9. A mérnökök egy gépkocsi mozgását figyelték műszerek segítségével négy másodpercen át. A pillanatnyi sebességek (m/s-ban

)

mért adataira a számítógép a következő függvényt illesztette:

\begin{matrix} v (t) = 2, 5 t^{3} - 16 t^{2} + 33 t + 5. \end{matrix}

a)

Mekkora sebességre gyorsult fel az autó az első másodperc végére?

b)

A sebességváltás pillanatában nem gyorsult az autó. Mikor volt ez?

c)

A gépkocsi pillanatnyi fogyasztását (centiliterben mérve) a következő függvény írja le:

\begin{matrix} F (t) = 2 \cdot 10^{- 2} \cdot (v' (t) + 50 t) . \end{matrix}

Hány centiliter üzemanyag fogyott az első két másodperc alatt? (16 pont)

Megoldás.

a)

Az első másodperc végére

\begin{matrix} v (t) = 2, 5 \cdot 1^{3} - 16 \cdot 1^{2} + 33 \cdot 1 + 5 = 24, 5 (m/s), \end{matrix}

azaz 88,2 km/h sebességre gyorsult fel.

b)

Amikor az autó nem gyorsul, akkor a

Δ t

idő alatti sebességváltozása nulla. Ezek szerint a sebesség deriváltjának nullahelyét keressük.

\begin{matrix} v' (t) = 7, 5 \cdot t^{2} - 32 \cdot t + 33 = 0. \end{matrix}

Ennek nullahelyei

t_{1} = 1, 745 s

-nál, illetve

t_{2} = 2, 522 s

-nál vannak. Ekkor nem gyorsult az autó, tehát ekkor lehettek a sebességváltás pillanatai. (Ehhez automata sebességváltót lehet elképzelni, mellyel a Forma-1 pilótái versenyeznek.)

c)

A megadott függvény a gépkocsi pillanatnyi fogyasztását adja meg. Az első két másodperc alatt a gépkocsi fogyasztását ennek a függvénynek a

[0; 2]

intervallumon vett határozott integrálja adja meg.

\begin{matrix} \int_{0}^{2} F (t) d t & = \int_{0}^{2} 2 \cdot 10^{- 2} \cdot (v' (t) + 50 t) d t = \\ = \int_{0}^{2} 2 \cdot 10^{- 2} \cdot (7, 5 \cdot t^{2} - 32 \cdot t + 33 + 50 t) d t = \\ = 2 \cdot 10^{- 2} {[7, 5 \frac{t^{3}}{3} + 18 \frac{t^{2}}{2} + 33 t]}_{0}^{2} = 2, 44 (cl). \end{matrix}

¹http://tananyag.geomatech.hu/.