,,A matematika a fizika része. A fizika kísérleti tudomány, a természettudomány része. A matematika a fizikának az a része, amelyben a kísérletek olcsók.'' E mondatokkal kezdte a matematika tanításáról szóló előadását (lásd [3]) a 20. század egyik zseniális matematikusa, Vlagyimir Igorevics Arnold (1937‐2010), aki a fizikai intuíciót a matematikai gondolkodás nélkülözhetetlen elemének tekintette (egyedi látásmódjáról bárki képet kaphat az idézett előadásából, illetve a magyarul középiskolai szakköri füzetként megjelent [2] könyvecskéjéből). Bár Arnold iménti kijelentése kissé merésznek tűnik, annyi mindenesetre bizonyos, hogy számos, tisztán matematikainak látszó eredmény mögött valójában a józan ész számára teljesen világos és természetes fizikai elvek bújnak meg. Ezek a rejtett gondolatok gyakran roppant váratlan helyeken bukkannak fel ‐ a [7] könyv például egy egész sereg meglepő összefüggésre világít rá ‐, és gyönyörű megnyilvánulásai a két tudományterület egymáshoz való szoros kötődésének.
Jelen írásunk célja is éppen az, hogy egy szép és talán kevéssé ismert példáját mutassuk annak, ahogyan egyszerű fizikai meggondolások matematikai álruhát öltenek. Mindössze ellenállásokat kell megfelelő módon összekapcsolni, és rögtön nevezetes egyenlőtlenségekhez jutunk, mint például a számtani és harmonikus közepek közötti egyenlőtlenség, a Milne-egyenlőtlenség, amely egy KöMaL feladat megoldásában is szerephez jutott, valamint a Minkowski-egyenlőtlenség egy speciális esete. Cikkünkben az említett egyenlőtlenségeket először ellenállás-hálózatokbeli fizikai megfontolások segítségével ,,bizonyítjuk'', majd matematikailag is igazoljuk, közben pedig a történeti hátterükről szintén szót ejtünk. Mindvégig csupán elemi eszközökre támaszkodunk, nagyrészt matematikára, az elején egy kis fizikával fűszerezve. Néhány eredményt feladat formájában fogalmazunk meg és tűzünk ki, ezzel elősegítve a témában való elmélyülést. Kezdődjön tehát a kaland.

 

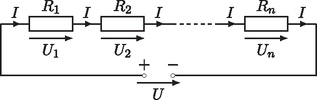1. ábra. Ellenállások soros kapcsolása

 

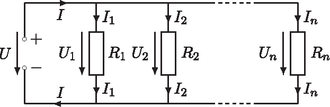2. ábra. Ellenállások párhuzamos kapcsolása

 

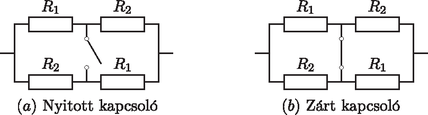3. ábra. Számtani és harmonikus közép elektromos hálózatokban

 

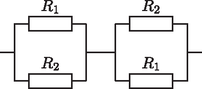4. ábra. Zárt kapcsoló esete átrajzolva

 

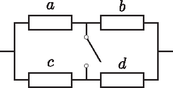5. ábra. A (4.2) egyenlőtlenség hálózata

 

4.3. megjegyzés. Az egyenlőség $ad=bc$ feltételét ‐ itt most lényeges, hogy $a$, $b$, $c$, $d$ nem lehetnek különböző előjelűek ‐ átfogalmazhatjuk úgy is, hogy az $\left(a\mathrm{,}b\right)$ és $\left(c\mathrm{,}d\right)$ síkbeli vektorok azonos irányúak (beleértve azt az esetet is, amikor valamelyik esetleg nullvektor). Valóban, ez utóbbi összefüggés azt jelenti, hogy van olyan $\lambda \ge 0$ szám, amelyre $a=\lambda c$ és $b=\lambda d$. Ha $\lambda =0$, akkor $\left(a\mathrm{,}b\right)=\left(\mathrm{0,0}\right)$, így a két vektor azonos irányú; ha pedig $\lambda >0$, akkor $d=b/\lambda$, és így $ad=\left(\lambda c\right)\cdot \left(b/\lambda \right)=bc$. Fordítva, amennyiben $ad=bc\ne 0$, akkor $a/c=b/d=\lambda >0$, hiszen ebben az esetben $a$, $b$, $c$, $d$ pozitív számok. Ha pedig $ad=bc=0$, akkor a szimmetria miatt feltehető, hogy $a=0$, ekkor $b=0$ vagy $c=0$; az első esetben $\left(a\mathrm{,}b\right)=\left(\mathrm{0,0}\right)$, míg a másodikban $\left(a\mathrm{,}b\right)=\left(\mathrm{0,}b\right)$, $\left(c\mathrm{,}d\right)=\left(\mathrm{0,}d\right)$, mindkétszer a kérdéses vektorok azonos irányúak.

 

4.4. feladat. Mutassuk meg, hogy nemnegatív $a\mathrm{,}b\mathrm{,}c\mathrm{,}d$ számok esetén az $\left(a\mathrm{,}b\right)$ és $\left(c\mathrm{,}d\right)$ vektorok pontosan akkor azonos irányúak, amikor az $\left(a\mathrm{,}c\right)$ és $\left(b\mathrm{,}d\right)$ vektorok azonos irányúak.

 

Bevezetve a

$\begin{array}{c}{\displaystyle H\left(x\mathrm{,}y\right)=\frac{2xy}{x+y}}\end{array}$

(4.3)

jelölést az $x$, $y$ nemnegatív és egyszerre nem nulla számok harmonikus közepére (a harmonikus közép eredeti formájában az $x\mathrm{,}y>0$ feltételezés lenne szükséges), a (4.2) egyenlőtlenség $2$-vel való szorzás után a következő, könnyen megjegyezhető alakot ölti:

$\begin{array}{c}{\displaystyle H\left(a+b\mathrm{,}c+d\right)\ge H\left(a\mathrm{,}c\right)+H\left(b\mathrm{,}d\right)\mathrm{.}}\end{array}$

(4.4)

 

4.5. feladat. Vizsgáljuk meg, hogy a (4.4) egyenlőtlenség (vagy esetleg a fordított iránya) igaz marad-e, ha a harmonikus közepet a számtani ($A\left(x\mathrm{,}y\right)$), mértani ($G\left(x\mathrm{,}y\right)$) és négyzetes ($Q\left(x\mathrm{,}y\right)$) közepek valamelyikére cseréljük, ahol

$\begin{array}{c}{\displaystyle A\left(x\mathrm{,}y\right)=\frac{x+y}{2}\mathrm{,}G\left(x\mathrm{,}y\right)=\sqrt[]{xy}\mathrm{,}Q\left(x\mathrm{,}y\right)=\sqrt[]{\frac{x^2+y^2}{2}}\mathrm{.}}\end{array}$

A (4.2) egyenlőtlenség akármelyik alakját is nézzük, azt gondolhatnánk, hogy valószínűleg nem tartozik a versenyfeladatokban leggyakrabban alkalmazott egyenlőtlenségek közé. Ez azonban nem feltétlenül igaz, hiszen a (4.2) egyenlőtlenség nemrég például a KöMaL-ban is felbukkant, méghozzá a 2012. májusi számban kitűzött B. 4461. és A. 563. jelű feladatok egyik megoldásában kapott szerepet (lásd a nyomtatásban és az interneten közölt [6] megoldásokat). Az említett feladatok cikkünk témakörén kívül esnek, ezért most ezekre nem térünk ki. Annyit viszont még mindenképpen megemlítünk, hogy a két feladat megoldásában valójában a (4.2) egyenlőtlenség alábbi általánosítására volt szükség.

 

4.6. állítás. Legyenek $a$, $b$, $c$, $d$ nemnegatív valós számok, amelyekre $a+c>0$ és $b+d>0$, továbbá legyen $p\ge 1$ valós szám. Ekkor

$\begin{array}{c}{\displaystyle {\left(a+b+c+d\right)}^{p-2}\left(a+b\right)\left(c+d\right)\ge {\left(a+c\right)}^{p-2}ac+{\left(b+d\right)}^{p-2}bd\mathrm{,}}\end{array}$

és egyenlőség csak abban az esetben áll fenn, ha $p=1$ és $ad=bc$.

 

4.7. feladat. Igazoljuk a 4.6. állítást (a $p=1$ eset ismeretében). (Segítség: ${\left(a+c\right)}^{p-2}={\left(a+c\right)}^{p-1}/\left(a+c\right)$.)

 

Térjünk vissza ezek után az ellenállásokra és folytassuk a Rayleigh-féle monotonitási törvény alkalmazásainak sorát.

 

5. A Milne-egyenlőtlenség

Egy további általánosítási lehetősége az 5. ábrán szereplő hálózatnak, ha két ellenállás helyett $n$ darabot kapcsolunk sorosan, majd két ilyen rendszert párhuzamosan kapcsolunk össze a 6. ábrán látható módon. Ekkor az összes kapcsolót nyitva hagyva, az egyes ágakban az eredő ellenállás $a_1+\text{...}+a_n$ és $b_1+\text{...}+b_n$, így az eredő ellenállás

$\begin{array}{c}{\displaystyle R_{\text{e}}^{\text{nyitott}}=\frac{\left(a_1+\text{...}+a_n\right)\left(b_1+\text{...}+b_n\right)}{a_1+\text{...}+a_n+b_1+\text{...}+b_n}\mathrm{.}}\end{array}$

 

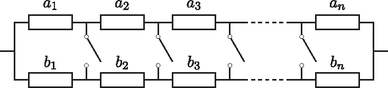6. ábra. Az (5.1) egyenlőtlenség hálózata

 

Zárt kapcsolók mellett a hálózat a 7. ábrán láthatóval egyenértékű, ahol párhuzamosan kapcsolt $a_i$, $b_i$ ellenállásokból álló komponensek vannak sorosan kapcsolva. Az egyes komponensek eredő ellenállása $a_i{b}_i/\left(a_i+b_i\right)$, ebből következően az összes kapcsoló zárása után a 6. ábra hálózatának eredő ellenállása

$\begin{array}{c}{\displaystyle R_{\text{e}}^{\text{zárt}}=\frac{a_1{b}_1}{a_1+b_1}+\text{...}+\frac{a_n{b}_n}{a_n+b_n}\mathrm{.}}\end{array}$

Mivel a Rayleigh-féle monotonitási törvény szerint $R_{\text{e}}^{\text{nyitott}}\ge R_{\text{e}}^{\text{zárt}}$, ezért $a_i+b_i>0$ ($i=\mathrm{1,}\text{...}\mathrm{,}n$) esetén várhatóan igaz a következő egyenlőtlenség:

$\begin{array}{c}{\displaystyle \frac{\left(a_1+\text{...}+a_n\right)\left(b_1+\text{...}+b_n\right)}{a_1+\text{...}+a_n+b_1+\text{...}+b_n}\ge \frac{a_1{b}_1}{a_1+b_1}+\text{...}+\frac{a_n{b}_n}{a_n+b_n}\mathrm{,}}\end{array}$

(5.1)

amit másképpen ($2$-vel való szorzás után) úgy is írhatunk, hogy

$\begin{array}{c}{\displaystyle H\left(a_1+\text{...}+a_n\mathrm{,}{b}_1+\text{...}+b_n\right)\ge H\left(a_1\mathrm{,}{b}_1\right)+\text{...}+H\left(a_n\mathrm{,}{b}_n\right)\mathrm{.}}\end{array}$

(5.2)

Ez $n=2$ esetén éppen a (4.2) egyenlőtlenség, ebből pedig teljes indukcióval nem nehéz belátni az általános esetet. Valóban, ha $n$-re igaz az (5.2) egyenlőtlenség, akkor az $a=a_1+\text{...}+a_n$, $b=a_{n+1}$, $c=b_1+\text{...}+b_n$, $d=b_{n+1}$ szereposztással a (4.2) egyenlőtlenségből azt kapjuk, hogy
${\displaystyle \begin{array}{c}\hfill {\displaystyle H\left(a_1+\text{...}+a_n+a_{n+1}\mathrm{,}{b}_1+\text{...}+b_n+b_{n+1}\right)\ge }\hfill \\ \hfill {\displaystyle \ge H\left(a_1+\text{...}+a_n\mathrm{,}{b}_1+\text{...}+b_n\right)+H\left(a_{n+1}\mathrm{,}{b}_{n+1}\right)\mathrm{,}}\hfill \end{array}}$

ahol a jobb oldalon az indukciós feltevés alkalmazásával éppen $\left(n+1\right)$-re adódik az (5.2) egyenlőtlenség.

 

7. ábra. A 6. ábra hálózata átrajzolva zárt kapcsolók esetén

 

Az iménti indukciós gondolatmenet segítségével azt sem nehéz igazolni, hogy egyenlőség csakis akkor áll fenn, ha az $\left(a_1\mathrm{,}\text{...}\mathrm{,}{a}_n\right)$ és $\left(b_1\mathrm{,}\text{...}\mathrm{,}{b}_n\right)$ vektorok azonos irányúak, amin azt értjük, hogy létezik $\lambda \ge 0$ szám, amellyel $a_i=\lambda b_i$ minden $i=\mathrm{1,}\text{...}\mathrm{,}n$ esetén. Valóban, az egyenlőség feltétele $n=2$ esetén a 4.3. megjegyzésből következik. Ha pedig $n$-re már tudjuk a feltételt, akkor az indukciós lépésből kiolvasható, hogy csak úgy lesz egyenlőség $\left(n+1\right)$-re, ha az indukciós feltevésben is egyenlőség áll fenn, tehát az $\left(a_1\mathrm{,}\text{...}\mathrm{,}{a}_n\right)$ és $\left(b_1\mathrm{,}\text{...}\mathrm{,}{b}_n\right)$ vektorok azonos irányúak, valamint az is szükséges, hogy az

$\begin{array}{c}{\displaystyle \left(a\mathrm{,}b\right)=\left(a_1+\text{...}+a_n\mathrm{,}{a}_{n+1}\right)}\end{array}$

és

$\begin{array}{c}{\displaystyle \left(c\mathrm{,}d\right)=\left(b_1+\text{...}+b_n\mathrm{,}{b}_{n+1}\right)=\left(\lambda \left(a_1+\text{...}+a_n\right)\mathrm{,}{b}_{n+1}\right)}\end{array}$

vektorok azonos irányúak legyenek. Ebből szükségképpen $a_{n+1}=\lambda b_{n+1}$ adódik, tehát az $\left(a_1\mathrm{,}\text{...}\mathrm{,}{a}_{n+1}\right)$ és $\left(b_1\mathrm{,}\text{...}\mathrm{,}{b}_{n+1}\right)$ vektorok azonos irányúak.
Érvényes tehát a következő állítás.

 

5.1. állítás. Legyenek $a_i$, $b_i$ $\left(i=\mathrm{1,}\text{...}\mathrm{,}n\right)$ nemnegatív számok, amelyekre $a_i+b_i>0$ minden $i=\mathrm{1,}\text{...}\mathrm{,}n$ esetén. Ekkor

$\begin{array}{c}{\displaystyle \frac{\left(a_1+\text{...}+a_n\right)\left(b_1+\text{...}+b_n\right)}{a_1+\text{...}+a_n+b_1+\text{...}+b_n}\ge \frac{a_1{b}_1}{a_1+b_1}+\text{...}+\frac{a_n{b}_n}{a_n+b_n}\mathrm{,}}\end{array}$

és egyenlőség pontosan akkor áll fenn, ha az $\left(a_1\mathrm{,}\text{...}\mathrm{,}{a}_n\right)$ és $\left(b_1\mathrm{,}\text{...}\mathrm{,}{b}_n\right)$ vektorok azonos irányúak.

 

Érdemes megjegyeznünk, hogy az 5.1. állítás előbbiekben bemutatott teljes indukciós bizonyítása mellett az általános esetben is működik az $n=2$ esetén alkalmazott (4.1) azonosságnak megfelelő négyzetösszeggé való alakítás ötlete. Ennek tömör és átlátható megfogalmazásához azonban célszerű bevezetnünk egy ‐ sokak számára bizonyára már ismerős ‐ jelölést.

 

5.2. jelölés. Ha $a_1\mathrm{,}\text{...}\mathrm{,}{a}_n$ tetszőleges valós számok, akkor

$\begin{array}{c}{\displaystyle \sum _{i=1}^n{a}_i:=a_1+a_2+\text{...}+a_n\mathrm{,}}\end{array}$

amit úgy olvasunk, hogy ,,szumma $i=1$-től $n$-ig $a_i$''. Használni fogjuk még a

$\begin{array}{c}{\displaystyle \sum _{1\le i<j\le n}^{}{a}_{ij}}\end{array}$

típusú jelölést is, amelyben ‐ magától értetődően ‐ az $1\le i<j\le n$ feltételt kielégítő összes $i$, $j$ indexpárra kell összegezni.

 

A szummás jelölés segítségével az 5.1. állítás valójában egy ‐ kis odafigyeléssel és türelemmel ‐ könnyen ellenőrizhető azonosságra vezethető vissza, amelyet az alábbi feladatban fogalmazunk meg (a feladat megoldása jó gyakorlási lehetőség a szummás jelölésmód elsajátításához).

 

5.3. feladat. Mutassuk meg, hogy
${\displaystyle \begin{array}{c}\hfill {\displaystyle \left({\sum }_{i=1}^n{a}_i\right)\left({\sum }_{i=1}^n{b}_i\right)-\left({\sum }_{i=1}^n\left(a_i+b_i\right)\right)\left({\sum }_{i=1}^n\frac{a_i{b}_i}{a_i+b_i}\right)={\sum }_{1\le i<j\le n}\frac{{\left(a_i{b}_j-a_j{b}_i\right)}^2}{\left(a_i+b_i\right)\left(a_j+b_j\right)}\mathrm{.}}\hfill \end{array}}$

 

5.4. történeti megjegyzés. Az 5.1. állításban szereplő egyenlőtlenséget az irodalomban szokás Milne-egyenlőtlenségnek is hívni. Edward Arthur Milne (1896‐1950) angol asztrofizikus és matematikus 1925-ben csillagászati vizsgálódásai kapcsán írta fel az egyenlőtlenség folytonos változatát integrálok segítségével (lásd a [9] cikket), és a bizonyítás közben lényegében megfogalmazta az általunk kimondott diszkrét változatot is. A Milne-egyenlőtlenség igazolását feladatként a neves kanadai, többnyire nehezebb versenyfeladatok kitűzésére specializálódott Crux Mathematicorum folyóirat is kitűzte 1996-ban. Egy évvel később három különböző megoldást jelentettek meg, amelyek egyike éppen az 5.3. feladatban szereplő azonosság (lásd [1]).

 

A szakasz zárásaként a nevezetes egyenlőtlenségekkel foglalkozó [4] könyvecske egy nehezebb feladatát idézzük, amely a Milne-egyenlőtlenség fényében szinte nyilvánvalóvá egyszerűsödik (ezért próbáljuk többféleképpen is megoldani, és a könyv megoldását is olvassuk el).

 

5.5. feladat. Bizonyítsuk be, hogy ha $a_1\mathrm{,}\text{...}\mathrm{,}{a}_n$ pozitív valós számok, akkor

$\begin{array}{c}{\displaystyle \frac{1}{\frac{1}{1+a_1}+\frac{1}{1+a_2}+\text{...}+\frac{1}{1+a_n}}-\frac{1}{\frac{1}{a_1}+\frac{1}{a_2}+\text{...}+\frac{1}{a_n}}\ge \frac{1}{n}\mathrm{.}}\end{array}$

 

Hivatkozások

[1]	F. Ardila, K. W. Lau, V. N. Murty, Solution to problem 2113, Crux Mathematicorum, 23 (1997), 112‐114. Elektronikus változat: https://cms.math.ca/crux/v23/n2/page112-128.pdf.

[2]	V. I. Arnold, Katasztrófaelmélet, Középiskolai Szakköri Füzetek, Tankönyvkiadó, Budapest, 1987.

[3]	V. I. Arnold, A matematika tanításáról (fordította: Kersner Róbert), Magyar Tudomány, 1998. október, 1247‐1251. Elektronikus változat angolul: http://pauli.uni-muenster.de/~munsteg/arnold.html.

[4]	Ábrahám Gábor, Nevezetes egyenlőtlenségek, MOZAIK Oktatási Stúdió, Szeged, 1995.

[5]	P. G. Doyle, J. L. Snell, Random Walks and Electric Networks, The Carus Mathematical Monographs, No. 22, Mathematical Association of America, Washington, DC, 1984. Elektronikus változat: https://math.dartmouth.edu/~doyle/docs/walks/walks.pdf.

[6]	KöMaL B. 4461. és A. 563. feladatok megoldása, KöMaL, 2012/5, 273‐274. Elektronikus változat: http://www.komal.hu/verseny/feladat.cgi?a=feladat&f=B4461.

[7]	M. Levi, The Mathematical Mechanic: Using Physical Reasoning to Solve Problems, Princeton University Press, Princeton, New Jersey, 2009.

[8]	J. C. Maxwell, A Treatise on Electricity and Magnetism, Volume 1, Calendron Press, Oxford, 1873. Elektronikus változat: https://archive.org/details/atreatiseonelec03maxwgoog.

[9]	E. A. Milne, Note on Rosseland's integral for the stellar absorption coefficient, Mon. Not. R. Astron. Soc., 85 (1925), 979‐984. Elektronikus változat: http://mnras.oxfordjournals.org/content/85/9/979.full.pdf.

[10]	A. Witkowski, Proof Without Words: An Electrical Proof of the AM-HM Inequality, Math. Mag., 87 (2014), 275. Elektronikus változat: http://www.jstor.org/stable/10.4169/math.mag.87.4.275.