| Cím: | Beszámoló a 2015. évi Eötvös-versenyről | ||
| Szerző(k): | Tichy Géza , Vankó Péter , Vigh Máté | ||
| Füzet: | 2016/január, 44 - 54. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az Eötvös Loránd Fizikai Társulat 2015. évi Eötvös-versenye október 16-án délután 3 órai kezdettel tizenöt magyarországi helyszínen1 került megrendezésre. Ezért külön köszönettel tartozunk mindazoknak, akik ebben szervezéssel, felügyelettel a segítségünkre voltak. A versenyen a három feladat megoldására 300 perc áll rendelkezésre, bármely írott vagy nyomtatott segédeszköz használható, de zsebszámológépen kívül minden elektronikus eszköz használata tilos. Az Eötvös-versenyen azok vehetnek részt, akik vagy középiskolai tanulók, vagy a verseny évében fejezték be középiskolai tanulmányaikat. Összesen 84 versenyző adott be dolgozatot, 21 egyetemista és 63 középiskolás. 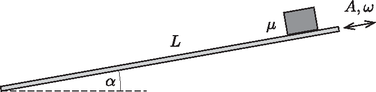 1. ábra 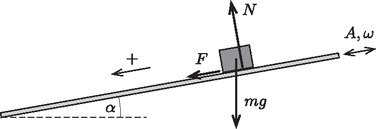 2. ábra Tapadás esetén a kényszererő és a súrlódási erő között az egyenlőtlenség áll fenn, míg csúszásnál . A hasáb gyorsulása akkor a lehető legnagyobb, ha a hasáb csúszik, és a hasáb deszkához viszonyított (relatív) sebessége negatív irányba mutat. Ekkor A hasáb gyorsulása a mozgás során tehát kétféle értéket vehet fel aszerint, hogy a súrlódási erő éppen a pozitív vagy negatív irányba mutat:
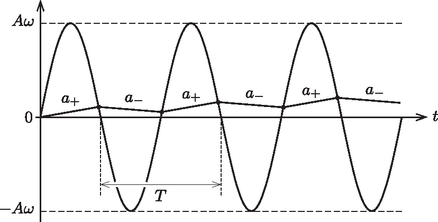 3. ábra A sodródási sebesség növekedése addig tart, amíg a hasáb átlaggyorsulása zérussá nem válik. Ezután a hasáb sebessége egy állandó érték körül fluktuál (4. ábra). Ez az állandósult (stacionárius) mozgás a viszonylag nagy rezgetési frekvencia miatt hamar kialakul, így a teljes mozgási idő becslésekor a kezdeti felgyorsulás időszakát el is hanyagolhatjuk. 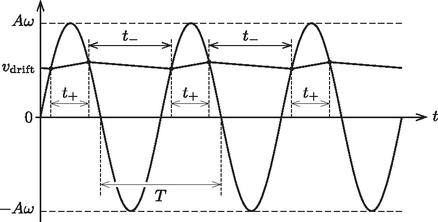 4. ábra Az állandósult sodródás feltétele:
A sodródási sebességet pedig abból a feltételből határozhatjuk meg, hogy a hasáb gyorsulása akkor vált irányt, amikor a deszka és a hasáb sebessége megegyezik. A sebesség ( értékéhez képest kicsiny) fluktuációját elhanyagolva: Hátravan még annak belátása, hogy a hasáb valóban nem tapad meg soha a lejtőn. A megtapadásnak két feltétele van: az egyik, hogy egy adott pillanatban a test és a deszkalap sebessége megegyezzen; a másik, hogy ugyanebben a pillanatban a deszka gyorsulásának nagysága kisebb legyen -nál vagy -nál aszerint, hogy a deszka épp lefelé vagy felfelé gyorsul. A sebesség-idő grafikonról látszik, hogy ez a két feltétel csak akkor következhet be, amikor a deszka gyorsulása nagyon kicsi, azaz sebessége nagy (-hoz közeli). Ekkora sebességre azonban nem tud felgyorsulni a hasáb, mert már előbb beáll a nála jóval kisebb . A hasáb tehát végig csúszva halad a lejtőn. Mekkora a lencse fókusztávolsága?  5. ábra Készítsünk vázlatot az optikai elrendezésről (6. ábra)! A rajzon három sík látható: a lencse síkja, a mérőszalag síkja és a látszólagos kép síkja. Az átmérők közül a lencse átmérője () meg van adva, a átmérőt leolvastuk a képről, a látszólagos kép átmérője pedig , ahol a képről leolvasott méret és a nagyítás. A távolságok közül a tárgytávolság (a lencse és a mérőszalag távolsága) meg van adva, a képtávolság és az távolság (a lencse és a fényképezőgép távolsága) egyelőre ismeretlen. 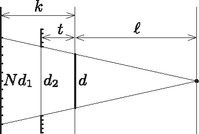 6. ábra A rajzon ábrázolt mennyiségek között egyszerű összefüggéseket írhatunk fel. A lencsetörvény alapján: Az egyenletrendszert rendezve (-t, -et és -et kiejtve): Mielőtt ebbe a kifejezésbe behelyettesítenénk a megadott és leolvasott adatokat, foglalkoznunk kell az adatok hibájával is! Nem véletlenül szerepel a szövegben és . A lencse átmérőjét tolómérővel meg lehet mérni, így az tizedmilliméter (századcentiméter) pontossággal megadható. A lencse és a mérőszalag távolsága már nem mérhető ilyen pontosan, hiszen a lencse vastagsága sem nulla ‐ ezt az adatot már csak milliméter pontosan adja meg a feladat szövege. A legkritikusabb a és távolságok minél pontosabb leolvasása, mert a fókusztávolság képletében ezek különbsége szerepel. Gondos megfigyeléssel ezek az átmérők néhány tizedmilliméter pontossággal leolvashatók a képről. A megadott és leolvasott adatok hibájából már a hibaszámítás ismert szabályai szerint meghatározható a fókusztávolság relatív hibája: A megadott és leolvasott adatok hibával: Ebből a numerikus eredmény: . A 7. ábra szerint a megadott adatok és a leolvasott ,,külső'' átmérő alapján hasonló háromszögek segítségével kifejezhető a lencse és a fényképezőgép távolsága: 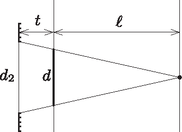 7. ábra A 8. ábrán az látható, hogy a nagyított képen még éppen látható pontokból (a ,,belső'' átmérő két széléről) induló (és a lencsén megtörve a fényképezőgépbe jutó) fénysugarak olyanok, mintha egy képzeletbeli pontból indulnának. A pont lencsétől mért távolsága az előzőhöz hasonló módon kifejezhető: 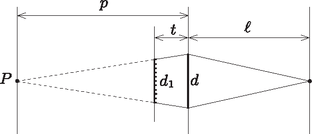 8. ábra A képzeletbeli pontból induló fénysugarak a lencsén megtörve éppen a fényképezőgépbe jutnak, így a lencsetörvény alapján 2. A versenyzők közül senki se foglalkozott a hibákkal, és a leolvasást is ,,nagyvonalúan'' végezték (a átmérőt legtöbben kereken cm-nek, mások cm-nek vették). Egy mm-es leolvasási hiba cm-es hibát okoz a fókusztávolságban ‐ ennek ellenére az eredményt legtöbben 4-5 értékes jegy pontossággal adták meg. Így erre a feladatra ‐ bár 16-an lényegében helyesen megoldották ‐ senki se adott teljes értékű megoldást. Mekkora effektív feszültséget mutat a lapos tekercsre kapcsolt (ideálisnak tekinthető) voltmérő? A lapos tekercsben nem folyik áram (a voltmérő ellenállása nagyon nagy), de a hosszú tekercs szórt mágneses tere feszültséget indukál benne. A feladat ennek a szórt térnek a meghatározása. A tekercsen kívüli mágneses mező ( miatt) jó közelítéssel olyan, mintha a tekercs egyik végén egy pontszerű forrásból összesen mágneses fluxus indulna ki gömbszimmetrikusan, a tekercs másik végén pedig ugyanekkora fluxus nyelődne el (vagyis mintha egy erősségű forrás helyezkedne el ott). A lapos tekercs a hosszú tekercs felezősíkjában, a hosszú tekercshez közel helyezkedik el, így ezen a helyen mindkét forrás külön-külön Az és feszültségek minden pillanatban arányosak egymással, így az effektív értékek aránya is ugyanekkora. Ebből a keresett feszültség: Ez az összefüggés azonban véges hosszúságú tekercsre csak közelítőleg igaz! A véges hosszúságú tekercs terét a tekercs középpontjában helyesen a következő kifejezés adja meg:  9. ábra Hosszú, vékony tekercsnél Írjuk fel a gerjesztési törvényt egy olyan kis téglalapra, amelynek két oldala a két tekercs tengelyén fekszik (10. ábra): 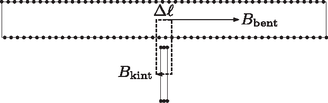 10. ábra A tekercsekben indukált feszültség arányos a tekercsek menetszámával és az egy meneten áthaladó fluxussal, amiből a keresett feszültség: 2. A véges hosszúságú tekercs terének levezetése. Egy sugarú körvezetőben folyó erősségű áram által keltett mágneses indukciót a kör síkjára merőleges szimmetriatengely pontjaiban könnyen kiszámíthatjuk a Biot‐Savart-törvény segítségével. A szimmetriatengely azon pontjában, ahonnan a körvezető sugara szögben látszik, tehát amely ponttól a körvezető pontjai távol vannak (11. ábra), a mágneses indukció 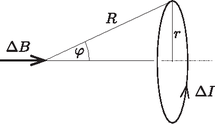 11. ábra Rakjuk össze az hosszúságú menetes tekercset vastagságú kis köráramokból. Ekkor egy ilyen kis körben 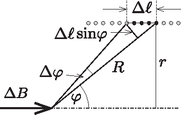 12. ábra Kihasználva, hogy a tekercs alkotójának kicsiny hosszúságú darabja a kérdéses pontból 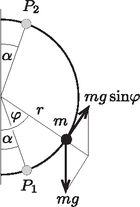 13. ábra Az ünnepélyes eredményhirdetésre és díjkiosztásra 2015. november 20-án délután került sor az ELTE TTK Harmónia termében. Meghívást kaptak az 50 és 25 évvel ezelőtti Eötvös-verseny nyertesei is. Gnädig Péter, az 50 évvel ezelőtti verseny egyik győztese külföldi útja miatt nem tudott eljönni, üzenetét Vankó Péter olvasta fel. Az akkori verseny másik győztese Juvancz Gábor, az ELTE fizikus hallgatója volt, aki nagyon fiatalon, közvetlenül a diplomája megszerzése után egy tragikus balesetben életét vesztette. A 25 évvel ezelőtti díjazottak közül Horváth Tibor és Maróti Miklós jött el az alkalomra, utóbbi az akkori feladatok ismertetése után röviden beszélt a versennyel kapcsolatos emlékeiről és pályájáról. Ezután következett a 2015. évi verseny feladatainak és megoldásainak bemutatása. Az 1. feladat megoldását Vigh Máté, a 2. feladatét Vankó Péter, a harmadik feladatét Tichy Géza ismertette. Ezután került sor az eredményhirdetésre. A díjakat Patkós András, az Eötvös Loránd Fizikai Társulat elnöke adta át. Egyetlen versenyző sem oldotta meg mindhárom feladatot, így a versenybizottság nem adott ki első díjat. Egy feladat helyes és egy feladat lényegében helyes megoldásáért második díjat nyert Fehér Zsombor, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium érettségizett tanulója, Horváth Gábor tanítványa ‐ jelenleg az ELTE matematikus hallgatója; Holczer András, a Pécsi Janus Pannonius Gimnázium érettségizett tanulója, Dombi Anna és Kotek László tanítványa ‐ jelenleg a BME villamosmérnök hallgatója; Juhász Dániel, a Szegedi Radnóti Miklós Kísérleti Gimnázium 12. osztályos tanulója, Csányi Sándor tanítványa; Sal Kristóf, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 12. osztályos tanulója, Kotek László és Horváth Gábor tanítványa valamint Tompa Tamás Lajos, a miskolci Földes Ferenc Gimnázium 11. osztályos tanulója, Zámborszky Ferenc és Kovács Benedek tanítványa. Egy feladat helyes megoldásáért és a hozzáfűzött diszkusszióért harmadik díjat nyert Balogh Menyhért, a budapesti Baár-Madas Református Gimnázium 12. osztályos tanulója, Horváth Norbert tanítványa. Egy feladat lényegében helyes megoldásáért dicséretben részesült Bege Áron, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 11. osztályos tanulója, Horváth Gábor és Szokolai Tibor tanítványa; Bencsik Bálint, az Óbudai Árpád Gimnázium 12. osztályos tanulója, Nagy Attila tanítványa; Bugár Dávid, a révkomáromi Selye János Gimnázium érettségizett tanulója, Szabó Endre tanítványa ‐ jelenleg az ELTE fizikus hallgatója; Forrai Botond, a budapesti Baár-Madas Református Gimnázium 12. osztályos tanulója, Horváth Norbert tanítványa; Frey Balázs, a Váci Szakképzési Centrum Boronkay György Műszaki Szakközépiskola és Gimnázium 12. osztályos tanulója, Tóth Eszter tanítványa; Gémes Antal, a hódmezővásárhelyi Bethlen Gábor Református Gimnázium 11. osztályos tanulója, Lakatos-Tóth István és Nagy Tibor tanítványa; Kasza Bence, a Budai Ciszterci Szent Imre Gimnázium 12. osztályos tanulója, Ábrám László és Sarkadi Tamás tanítványa; Kovács Péter Tamás, a Zalaegerszegi Zrínyi Miklós Gimnázium 11. osztályos tanulója, Juhász Tibor és Pálovics Róbert tanítványa; Körmöczi Dávid, az Egri Szilágyi Erzsébet Gimnázium és Kollégium 12. osztályos tanulója, Szabó Miklós tanítványa; Olosz Balázs, a PTE Babits Mihály Gyakorló Gimnázium érettségizett tanulója, Koncz Károly tanítványa ‐ jelenleg a BME villamosmérnök hallgatója; Szamosfalvi Benjámin Balázs, a Miskolci Herman Ottó Gimnázium 12. osztályos tanulója, Dudás Imre tanítványa; Szick Dániel, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 12. osztályos tanulója, Horváth Gábor tanítványa; Tomcsányi Gergely, a Váci Szakképzési Centrum Boronkay György Műszaki Szakközépiskola és Gimnázium 12. osztályos tanulója, Tóth Eszter tanítványa valamint Török Péter, a Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium 11. osztályos tanulója, Horváth Gábor és Szokolai Tibor tanítványa. A MOL támogatásával a második díjjal nettó 25 ezer, a harmadik díjjal nettó 20 ezer forint pénzjutalom járt, a dicséretes versenyzők valamint a díjazottak tanárai pedig a versenyt támogató Typotex Kiadó könyveit kapták. 1Részletek a verseny honlapján: http://mono.eik.bme.hu/vanko/fizika/eotvos.htm. |