Cím:	A 46. Nemzetközi Fizikai Diákolimpia feladatainak megoldása
Szerző(k):	Szász Krisztián ,  Vankó Péter ,  Vigh Máté
Füzet:	2015/november, 485 - 497. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1   Elméleti feladatok   1. feladat. A Napból érkező részecskék A rész. A Naptól jövő sugárzás A.1. A Stefan‐Boltzmann-törvény alapján: $L_{\odot }=\left(4\pi R_{\odot }^2\right)\left(\sigma T_{\odot }^4\right)$. Innen: $\begin{array}{c}{\displaystyle T_{\odot }={\left(\frac{L_{\odot }}{4\pi R_{\odot }^2\sigma }\right)}^{1/4}=5\mathrm{,}76\cdot {10}^3\text{ K}\mathrm{.}}\end{array}$ A.2. $\begin{array}{c}{\displaystyle P_{\text{be}}=\underset{0}{\overset{\infty }{\int }}u\left(f\right)\text{d}f=\underset{0}{\overset{\infty }{\int }}A\frac{R_{\odot }^2}{d_{\odot }^2}\frac{2\pi h}{c^2}{f}^3\text{exp}\left(-hf/k_{\text{B}}{T}_{\odot }\right)\text{d}f\mathrm{.}}\end{array}$ Legyen $x=\frac{hf}{k_{\text{B}}{T}_{\odot }}$. Ekkor $f=\frac{k_{\text{B}}{T}_{\odot }}{h}x$ és $\text{d}f=\frac{k_{\text{B}}{T}_{\odot }}{h}\text{d}x$. Ezzel: $\begin{array}{c}{\displaystyle P_{\text{be}}=\frac{2\pi hA{R}_{\odot }^2}{c^2{d}_{\odot }^2}\frac{{\left(k_{\text{B}}{T}_{\odot }\right)}^4}{h^4}\underset{0}{\overset{\infty }{\int }}{x}^3{\text{e}}^{-x}\text{d}x=\frac{2\pi k_{\text{B}}^4}{c^2{h}^3}{T}_{\odot }^{4}A\frac{R_{\odot }^2}{d_{\odot }^2}\cdot 6=\frac{12\pi k_{\text{B}}^4}{c^2{h}^3}{T}_{\odot }^{4}A\frac{R_{\odot }^2}{d_{\odot }^2}\mathrm{.}}\end{array}$ Másik megoldás, amely nem használja a Wien-közelítést: $\begin{array}{c}{\displaystyle P_{\text{be}}=\frac{L_{\odot }}{4\pi d_{\odot }^2}A=\sigma T_{\odot }^{4}A\frac{R_{\odot }^2}{d_{\odot }^2}=\frac{2{\pi }^5{k}_{\text{B}}^4}{15c^2{h}^3}{T}_{\odot }^{4}A\frac{R_{\odot }^2}{d_{\odot }^2}\mathrm{.}}\end{array}$ A.3. $\begin{array}{c}{\displaystyle n_{\gamma }\left(f\right)=\frac{u\left(f\right)}{hf}=A\frac{R_{\odot }^2}{d_{\odot }^2}\frac{2\pi }{c^2}{f}^2\text{exp}\left(-hf/k_{\text{B}}{T}_{\odot }\right)\mathrm{.}}\end{array}$ A.4. A hasznos kimenő teljesítményt az $E_{\text{g}}=h{f}_{\text{g}}$ egy fotonra jutó energiakvantum és az $E\ge E_{\text{g}}$ energiájú fotonok számának szorzata adja: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P_{\text{ki}}}& {\displaystyle =h{f}_{\text{g}}{\int }_{f_{\text{g}}}^{\infty }{n}_{\gamma }\left(f\right)\text{d}f=h{f}_{\text{g}}A\frac{R_{\odot }^2}{d_{\odot }^2}\frac{2\pi }{c^2}{\int }_{f_{\text{g}}}^{\infty }{f}^2\text{exp}\left(-hf/k_{\text{B}}{T}_{\odot }\right)\text{d}f=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =k_{\text{B}}{T}_{\odot }{x}_{\text{g}}A\frac{R_{\odot }^2}{d_{\odot }^2}\frac{2\pi }{c^2}{\left(\frac{k_{\text{B}}{T}_{\odot }}{h}\right)}^3{\int }_{x_{\text{g}}}^{\infty }{x}^2{\text{e}}^{-x}\text{d}x=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{2\pi k_{\text{B}}^4}{c^2{h}^3}{T}_{\odot }^{4}A\frac{R_{\odot }^2}{d_{\odot }^2}{x}_{\text{g}}\left(x_{\text{g}}^2+2x_{\text{g}}+2\right){\text{e}}^{-x_{\text{g}}}\mathrm{.}}\hfill \end{array}}$ A.5. A hatásfok: $\begin{array}{c}{\displaystyle \eta =\frac{P_{\text{ki}}}{P_{\text{be}}}=\frac{x_{\text{g}}}{6}\left(x_{\text{g}}^2+2x_{\text{g}}+2\right){\text{e}}^{-x_{\text{g}}}\mathrm{.}}\end{array}$ Ha $P_{\text{be}}$-re az A.2. másik eredményét használjuk, akkor a hatásfok: $\begin{array}{c}{\displaystyle \eta =\frac{2\pi k_{\text{B}}^4}{c^2{h}^3}\frac{1}{\sigma }{x}_{\text{g}}\left(x_{\text{g}}^2+2x_{\text{g}}+2\right){\text{e}}^{-x_{\text{g}}}=\left(\frac{90}{{\pi }^4}\right)\frac{x_{\text{g}}}{6}\left(x_{\text{g}}^2+2x_{\text{g}}+2\right){\text{e}}^{-x_{\text{g}}}\mathrm{.}}\end{array}$ A két eredmény közel van egymáshoz, mert 90/${\pi }^4\approx 0\mathrm{,}92\approx 1$. A.6. $\begin{array}{c}{\displaystyle \eta =\frac{1}{6}\left(x_{\text{g}}^3+2x_{\text{g}}^2+2x_{\text{g}}\right){\text{e}}^{-x_{\text{g}}}\mathrm{.}}\end{array}$ A határokon érvényes értékek: $\eta \left(0\right)=0$ és $\eta \left(\infty \right)=0$. Mivel a zárójelben levő polinom kizárólag pozitív együtthatókat tartalmaz, az monoton növekvő. Az exponenciális függvény monoton csökkenő, és a szorzatuknak valahol maximuma van. ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{\text{d}\eta }{\text{d}{x}_{\text{g}}}=\frac{1}{6}\left(-x_{\text{g}}^3+x_{\text{g}}^2+2x_{\text{g}}+2\right){\text{e}}^{-x_{\text{g}}}\mathrm{,}}\hfill \\ \hfill {\displaystyle {\frac{\text{d}\eta }{\text{d}{x}_{\text{g}}}|}_{x_{\text{g}}=0}=\frac{1}{3}\mathrm{,}{\frac{\text{d}\eta }{\text{d}{x}_{\text{g}}}|}_{x_{\text{g}}\to \infty }=0.}\hfill \end{array}}$ Ha az A.2. másik eredményét használjuk, akkor: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{\text{d}\eta }{\text{d}{x}_{\text{g}}}=\frac{15}{{\pi }^4}\left(-x_{\text{g}}^3+x_{\text{g}}^2+2x_{\text{g}}+2\right){\text{e}}^{-x_{\text{g}}}\mathrm{,}}\hfill \\ \hfill {\displaystyle {\frac{\text{d}\eta }{\text{d}{x}_{\text{g}}}|}_{x_{\text{g}}=0}=\frac{30}{{\pi }^4}\approx 0\mathrm{,}\mathrm{31,}{\frac{\text{d}\eta }{\text{d}{x}_{\text{g}}}|}_{x_{\text{g}}\to \infty }=0.}\hfill \end{array}}$     A.7. A maximális értéket ott veszi fel a függvény, ahol ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{\text{d}\eta }{\text{d}{x}_{\text{g}}}=\frac{1}{6}\left(-x_{\text{g}}^3+x_{\text{g}}^2+2x_{\text{g}}+2\right){\text{e}}^{-x_{\text{g}}}=0\Rightarrow p\left(x_{\text{g}}\right)\equiv x_{\text{g}}^3-x_{\text{g}}^2-2x_{\text{g}}-2=0.}\hfill \end{array}}$ Az egyenlet megoldásához használhatjuk például a felező módszert (más numerikus módszer is elfogadható): ${\displaystyle \begin{array}{cc}\hfill {\displaystyle p\left(0\right)}& {\displaystyle =-\mathrm{2,}}\hfill \\ \hfill {\displaystyle p\left(1\right)}& {\displaystyle =-\mathrm{4,}}\hfill \\ \hfill {\displaystyle p\left(2\right)}& {\displaystyle =-\mathrm{2,}}\hfill \\ \hfill {\displaystyle p\left(3\right)}& {\displaystyle =10\Rightarrow 2<x_0<\mathrm{3,}}\hfill \\ \hfill {\displaystyle p\left(2\mathrm{,}5\right)}& {\displaystyle =2\mathrm{,}375\Rightarrow 2<x_0<2\mathrm{,}\mathrm{5,}}\hfill \\ \hfill {\displaystyle p\left(2\mathrm{,}25\right)}& {\displaystyle =-0\mathrm{,}171\Rightarrow 2\mathrm{,}25<x_0<2\mathrm{,}5.}\hfill \end{array}}$ A közelítő érték, ahol $\eta$-nak maximuma van: $x_0=2\mathrm{,}27$. A maximum: $\eta \left(2\mathrm{,}27\right)=0\mathrm{,}457$. A.8. Az $x_{\text{g}}$ értéke: $\begin{array}{c}{\displaystyle x_{\text{g}}=\frac{1\mathrm{,}11\cdot 1\mathrm{,}60\cdot {10}^{-19}}{1\mathrm{,}38\cdot {10}^{-23}\cdot 5763}=2\mathrm{,}\mathrm{23,}}\end{array}$ amivel a hatásfok: $\begin{array}{c}{\displaystyle {\eta }_{\text{Si}}=\frac{x_{\text{g}}}{6}\left(x_{\text{g}}^2+2x_{\text{g}}+2\right){\text{e}}^{-x_{\text{g}}}=0\mathrm{,}457.}\end{array}$ Ha az A.2. másik eredményét használjuk, akkor: $\begin{array}{c}{\displaystyle {\eta }_{\text{Si}}=\frac{15x_{\text{g}}}{{\pi }^4}\left(x_{\text{g}}^2+2x_{\text{g}}+2\right){\text{e}}^{-x_{\text{g}}}=0\mathrm{,}422.}\end{array}$ A.9. A Nap teljes gravitációs potenciális energiája: $\begin{array}{c}{\displaystyle \Omega =-\underset{0}{\overset{M_{\odot }}{\int }}\frac{Gm\text{d}m}{r}\mathrm{.}}\end{array}$ Az egyenletes tömegeloszlás miatt: $\begin{array}{c}{\displaystyle \varrho =\frac{3M_{\odot }}{4\pi R_{\odot }^3}\mathrm{,}m=\frac{4}{3}\pi r^3\varrho \mathrm{,}\text{d}m=4\pi r^2\varrho \text{d}r\mathrm{.}}\end{array}$ Ezzel: $\begin{array}{c}{\displaystyle \Omega =-\underset{0}{\overset{R_{\odot }}{\int }}G\left(\frac{4}{3}\pi r^3\varrho \right)\left(4\pi r^2\varrho \right)\frac{\text{d}r}{r}=-\frac{16{\pi }^{2}G{\varrho }^2}{3}\frac{R_{\odot }^5}{5}=-\frac{3}{5}\frac{G{M}_{\odot }^2}{R_{\odot }}\mathrm{.}}\end{array}$ A.10. $\begin{array}{c}{\displaystyle {\tau }_{\text{KH}}=\frac{-\Omega }{L_{\odot }}=\frac{3G{M}_{\odot }^2}{5R_{\odot }{L}_{\odot }}=1\mathrm{,}88\cdot {10}^7\text{ év}\mathrm{.}}\end{array}$   B rész. A Napból jövő neutrínók B.1. $\Delta E$ energia felszabadulása során két neutrínó keletkezik, így $\begin{array}{c}{\displaystyle {\Phi }_{\nu }=2\cdot \frac{L_{\odot }}{4\pi d_{\odot }^2\Delta E}=2\cdot \frac{3\mathrm{,}85\cdot {10}^{26}}{4\pi \cdot {\left(1\mathrm{,}50\cdot {10}^{11}\right)}^2\cdot 4\mathrm{,}0\cdot {10}^{-12}}=6\mathrm{,}8\cdot {10}^{14}{\text{ m}}^{-2}{\text{s}}^{-2}\mathrm{.}}\end{array}$ B.2. Legyen $\epsilon$ a neutrínó detektálásának hatásfoka, $N_0$ a bejövő részecskeszám. Ezzel: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle N_1}& {\displaystyle =\epsilon N_0\mathrm{,}}\hfill \\ \hfill {\displaystyle N_{\text{e}}}& {\displaystyle =\epsilon N_0\left(1-r\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle N_{\text{x}}}& {\displaystyle =\epsilon N_{0}r/\mathrm{6,}}\hfill \\ \hfill {\displaystyle N_2}& {\displaystyle =N_{\text{e}}+N_{\text{x}}\mathrm{.}}\hfill \end{array}}$ Tehát: $\begin{array}{c}{\displaystyle \left(1-r\right)N_1+\frac{r}{6}{N}_1=N_2\mathrm{,}}\end{array}$ innen a kérdezett hányados: $\begin{array}{c}{\displaystyle r=\frac{6}{5}\left(1-\frac{N_2}{N_1}\right)\mathrm{.}}\end{array}$ B.3. Amikor egy elektron már éppen nem bocsát ki Cserenkov-sugárzást, a sebessége $v_{\text{stop}}=c/n$-re csökken. Az elektron teljes energiája ekkor: $\begin{array}{c}{\displaystyle E_{\text{stop}}=\frac{m_{\text{e}}{c}^2}{\sqrt[]{1-v_{\text{stop}}^2/c^2}}=\frac{n{m}_{\text{e}}{c}^2}{\sqrt[]{n^2-1}}\mathrm{.}}\end{array}$ Abban a pillanatban, miután a neutrínó kiütötte az elektront, az elektron energiája: $\begin{array}{c}{\displaystyle E_{\text{start}}=\alpha \Delta t+\frac{n{m}_{\text{e}}{c}^2}{\sqrt[]{n^2-1}}\mathrm{.}}\end{array}$ A kölcsönhatás előtt az elektron energiája $m_{\text{e}}{c}^2$. Így a neutrínónak átadott energia: $\begin{array}{c}{\displaystyle E_{\text{átadott}}=E_{\text{start}}-m_{\text{e}}{c}^2=\alpha \Delta t+\left(\frac{n}{\sqrt[]{n^2-1}}-1\right)m_{\text{e}}{c}^2\mathrm{.}}\end{array}$ B.4. A ${}^7$Be atommagok mozgása miatt Doppler-effektus lép fel a neutrínókra. Mivel az energia relatív megváltozása kicsiny ($\Delta E_{\text{rms}}/E_{\nu }\sim {10}^{-4}$), a nemrelativisztikus Doppler-eltolódással lehet számolni (a relativisztikus számolás szinte azonos eredményt ad). A megfigyelés irányának a $z$ irányt véve: $\begin{array}{c}{\displaystyle \frac{\Delta E_{\text{rms}}}{E_{\nu }}=\frac{v_{z\mathrm{,}\text{rms}}}{c}=\frac{\frac{1}{\sqrt[]{3}}{V}_{\text{Be}}}{c}=3\mathrm{,}85\cdot {10}^{-4}\mathrm{.}}\end{array}$ Tehát a Be atommagok sebességének négyzetes középértéke: $\begin{array}{c}{\displaystyle V_{\text{Be}}=\sqrt[]{3}\cdot 3\mathrm{,}85\cdot {10}^{-4}\cdot 3\mathrm{,}00\cdot {10}^8{\text{ ms}}^{-1}=2\mathrm{,}01\cdot {10}^5{\text{ ms}}^{-1}\mathrm{.}}\end{array}$ A Nap magjának átlagos hőmérséklete pedig: $\begin{array}{c}{\displaystyle \frac{1}{2}{m}_{\text{Be}}{V}_{\text{Be}}^2=\frac{3}{2}{k}_{\text{B}}{T}_{\text{c}}\Rightarrow T_{\text{c}}=1\mathrm{,}13\cdot {10}^7\text{ K}\mathrm{.}}\end{array}$   2. feladat. A szélsőértékelv A rész. Szélsőértékelv a mechanikában A.1. A mechanikai energia megmaradása alapján: $\begin{array}{c}{\displaystyle \frac{1}{2}m{v}_1^2=\frac{1}{2}m{v}_2^2+V_0\mathrm{,}\text{amiből}{v}_2=\sqrt[]{v_1^2-\frac{2V_0}{m}}\mathrm{.}}\end{array}$ A.2. A határfelületen csak az $x$ irányú sebességkomponens változik (a határfelületen fellépő $-x$ irányú erőlökés hatására), az $y$ irányú nem. Ezért ${\displaystyle \begin{array}{cc}\hfill {\displaystyle v_{1y}}& {\displaystyle =v_{2y}\mathrm{,}}\hfill \\ \hfill {\displaystyle v_1\text{sin}{\vartheta }_1}& {\displaystyle =v_2\text{sin}{\vartheta }_2\mathrm{.}}\hfill \end{array}}$ A.3. A hatás definíciójának megfelelően $A\left(w\right)$ az $O$ és $P$ rögzített pontok között: $\begin{array}{c}{\displaystyle A\left(w\right)=m{v}_1\sqrt[]{x_1^2+w^2}+m{v}_2\sqrt[]{{\left(x_0-x_1\right)}^2+\left(y_0^2-w^2\right)}\mathrm{.}}\end{array}$ Az $A\left(w\right)$ hatás akkor lesz minimális, ha $w$ szerinti deriváltja nulla: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{v_{1}w}{\sqrt[]{x_1^2+w^2}}-\frac{v_2\left(y_0-w\right)}{\sqrt[]{{x_0-x_1)}^2+{\left(y_0-w\right)}^2}}=\mathrm{0,}}\hfill \\ \hfill {\displaystyle \frac{v_1}{v_2}=\frac{\left(y_0-w\right)\sqrt[]{x_1^2+w^2}}{w\sqrt[]{{\left(x_0-x_1\right)}^2+{\left(y_0-w\right)}^2}}\mathrm{.}}\hfill \end{array}}$ Vegyük észre, hogy ez ugyanaz, mint az A.2.-ben megkapott $v_1\text{sin}{\vartheta }_1=v_2\text{sin}{\vartheta }_2$ eredmény!   B rész. Szélsőértékelv az optikában B.1. A fény sebessége az I-es közegben $c/n_1$, a II-es közegben $c/n_2$, ahol $c$ a fénysebesség vákuumban. Legyen a két közeget elválasztó egyenes egyenlete $y=y_0$, a fénysugár pedig az $x=w$ helyen lépjen át egyik közegből a másikba. Az a $\tau \left(w\right)$ idő, amíg a fény a $\left(0;0\right)$ origóból a rögzített $\left(x_0;y_0\right)$ pontba jut: $\begin{array}{c}{\displaystyle \tau \left(w\right)=\frac{n_1}{c}\sqrt[]{y_1^2+w^2}+\frac{n_2}{c}\sqrt[]{{\left(x_0-w\right)}^2+{\left(y_0-y_1\right)}^2}\mathrm{.}}\end{array}$ A szélsőértéket A.3.-hoz hasonlóan deriválással határozhatjuk meg: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{n_{1}w}{\sqrt[]{y_1^2+w^2}}-\frac{n_2\left(y_0-w\right)}{\sqrt[]{{\left(x_0-w\right)}^2+{\left(y_0-y_1\right)}^2}}=\mathrm{0,}}\hfill \\ \hfill {\displaystyle n_1\text{sin}{\alpha }_1=n_2\text{sin}{\alpha }_2\mathrm{.}}\hfill \end{array}}$ Ez a Snellius‐Descartes-törvény. B.2. A Snellius‐Descartes-törvény alapján $n_0\text{sin}{\alpha }_0=n\left(y\right)\text{sin}\alpha$. Ezen kívül felhasználva, hogy $\text{d}y/\text{d}x=-\text{ctg}\alpha$ és $\text{sin}\alpha =1/\sqrt[]{1+\text{ctg}{}^2\alpha }$: ${\displaystyle \begin{array}{c}\hfill {\displaystyle n_0\text{sin}{\alpha }_0=\frac{n\left(y\right)}{\sqrt[]{1+{\left(\frac{\text{d}y}{\text{d}x}\right)}^2}}\mathrm{,}\frac{\text{d}y}{\text{d}x}=-\sqrt[]{{\left(\frac{n\left(y\right)}{n_0\text{sin}{\alpha }_0}\right)}^2-1}\mathrm{.}}\hfill \end{array}}$ B.3. A B.2. eredményből a változókat szétválasztva és mindkét oldalt integrálva: $\begin{array}{c}{\displaystyle \int \frac{\text{d}y}{\sqrt[]{{\left(\frac{n_0-ky}{n_0}\right)}^2-1}}=-\int \text{d}x\mathrm{.}}\end{array}$ (Felhasználtuk, hogy ${\alpha }_0={90}^{\circ }$ és így $\text{sin}{\alpha }_0=1$.) Használjuk a $\xi =\left(n_0-ky\right)/n_0$ helyettesítést, így: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \int \frac{\text{d}\xi \left(-\frac{n_0}{k}\right)}{\sqrt[]{{\xi }^2-1}}=-\int \text{d}x\mathrm{,}-\frac{n_0}{k}\text{ln}\left(\frac{n_0-ky}{n_0}+\sqrt[]{{\left(\frac{n_0-ky}{n_0}\right)}^2-1}\right)=-x+c\mathrm{.}}\hfill \end{array}}$ Figyelembe véve az $x=0$ és $y=0$ kezdeti feltételeket $c=0$. Ebből a pálya egyenlete: $\begin{array}{c}{\displaystyle x=\frac{n_0}{k}\text{ln}\left[\left(\frac{n_0-ky}{n_0}\right)+\sqrt[]{{\left(\frac{n_0-ky}{n_0}\right)}^2-1}\right]\mathrm{.}}\end{array}$ B.4. Felhasználva a megadott adatokat ($y_0=10\mathrm{,}0\text{cm}$, $n_0=1\mathrm{,}50$, $k=0\mathrm{,}050\text{c<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mo stretchy="false">-</mo><mn>1</mn></mrow></msup></mrow></math>}$) a B.3. végeredményébe behelyettesítve $\left(y=-y_0\right)$: $\begin{array}{c}{\displaystyle x_0=\frac{n_0}{k}\text{ln}\left[\left(\frac{n_0+k{y}_0}{n_0}\right)+\sqrt[]{{\left(\frac{n_0+k{y}_0}{n_0}\right)}^2-1}\right]=24\mathrm{,}0\text{cm}\mathrm{.}}\end{array}$   C rész. A szélsőértékelv és az anyag hullámtermészete C.1. 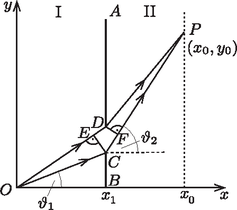A részecske de Broglie-hullámhossza $\lambda =\frac{h}{mv}$, amiből a keresett fáziskülönbség (a hatás $\Delta A=mv\Delta s$ definícióját felhasználva): $\begin{array}{c}{\displaystyle \Delta \phi =\frac{2\pi }{\lambda }\Delta s=\frac{2\pi }{h}mv\Delta s=\frac{2\pi \Delta A}{h}\mathrm{.}}\end{array}$   C.2. Tanulmányozzuk az $OCP$ és $ODP$ pályákat! A geometriai útkülönbség az I-es tartományban $ED$, a II-es tartományban $CF$. Ebből $d\ll x_0-x_1$ és $d\ll x_1$ felhasználásával ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \Delta {\phi }_{CD}}& {\displaystyle =\frac{2\pi d\text{sin}{\vartheta }_1}{{\lambda }_1}-\frac{2\pi d\text{sin}{\vartheta }_2}{{\lambda }_2}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{2\pi m{v}_{1}d\text{sin}{\vartheta }_1}{h}-\frac{2\pi m{v}_{2}d\text{sin}{\vartheta }_2}{h}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =2\pi \frac{md}{h}\left(v_1\text{sin}{\vartheta }_1-v_2\text{sin}{\vartheta }_2\right)=0}\hfill \end{array}}$ (A.2. vagy B.1. alapján). Ez az eredmény várható, hiszen a klasszikus pálya közelében erősítésnek kell lennie.       D rész. Anyaghullámok interferenciája D.1. Az energiák alapján $\begin{array}{c}{\displaystyle q{U}_1=\frac{1}{2}m{v}^2\mathrm{,}\text{amiből}{U}_1=\frac{m{v}^2}{2q}=1\mathrm{,}139\cdot {10}^3\text{V}\mathrm{.}}\end{array}$ D.2. A fáziskülönbség $P$-ben: $\begin{array}{c}{\displaystyle \Delta {\phi }_{\text{P}}=\frac{2\pi d\text{sin}\vartheta }{{\lambda }_1}-\frac{2\pi d\text{sin}\vartheta }{{\lambda }_2}=2\pi \left(v_1-v_2\right)\frac{md}{h}\text{sin}\vartheta =2\pi \beta \mathrm{,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle \beta =5\mathrm{,}13.}\end{array}$ D.3. Az előző rész alapján látható, hogy a legközelebbi olyan helyen, ahol nem várható elektronbecsapódás (kioltás van) $\Delta \phi =5\mathrm{,}5\cdot 2\pi$. Ez alapján: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{m{v}_{1}d\text{sin}\vartheta }{h}-\frac{m{v}_{2}d\text{sin}\left(\vartheta +\Delta \vartheta \right)}{h}=5\mathrm{,}5;}\hfill \\ \hfill {\displaystyle \text{sin}\left(\vartheta +\Delta \vartheta \right)=\frac{\frac{m{v}_{1}d\text{sin}\vartheta }{h}-5\mathrm{,}5}{\frac{m{v}_{2}d}{h}}=\frac{v_1}{v_2}\text{sin}\vartheta -\frac{5\mathrm{,}5h}{m{v}_{2}d}=0\mathrm{,}173\mathrm{586,}}\hfill \\ \hfill {\displaystyle \Delta \vartheta =-0\mathrm{,}{0036}^{\circ }\mathrm{,}}\hfill \end{array}}$ amiből a $P$-hez legközelebbi hely távolsága: $\begin{array}{c}{\displaystyle \Delta y=\left(x_0-x_1\right)\left[\text{tg}\left(\vartheta +\Delta \vartheta \right)-\text{tg}\vartheta \right]=-16\mathrm{,}2\mu \text{m}\mathrm{.}}\end{array}$ A negatív előjel azt mutatja, hogy ez a pont $P$ alatt van. D.4. Az $I$ fluxussűrűség az elektronok $v$ sebességének és $N/V$ sűrűségének szorzata. Ez alapján: $\begin{array}{c}{\displaystyle N=\frac{I_{\underset{}{\overset{}{\text{min}}}}V}{v}=\mathrm{1,}\text{amiből}{I}_{\underset{}{\overset{}{\text{min}}}}=\frac{v}{V}=\frac{v}{Al}=4\cdot {10}^{19}{\text{m}}^{-2}{\text{s}}^{-1}\mathrm{.}}\end{array}$   3. feladat. Nukleáris reaktor tervezése A rész. Az üzemanyagrúd A.1. A magreakció során felszabaduló energiát a tömegdefektusból számolhatjuk: $\begin{array}{c}{\displaystyle \Delta E=\left[m\left({}^{235}\text{<span style="font-weight: normal;font-style: normal;">U</span>}\right)+m\left({}^1\text{<span style="font-weight: normal;font-style: normal;">n</span>}\right)-m\left({}^{94}\text{<span style="font-weight: normal;font-style: normal;">Zr</span>}\right)-m\left({}^{140}\text{<span style="font-weight: normal;font-style: normal;">Ce</span>}\right)-2m\left({}^1\text{<span style="font-weight: normal;font-style: normal;">n</span>}\right)\right]c^2\mathrm{.}}\end{array}$ Összevonás után, a tömegek felhasználásával kapjuk: $\begin{array}{c}{\displaystyle \Delta E=\left[m\left({}^{235}\text{<span style="font-weight: normal;font-style: normal;">U</span>}\right)-m\left({}^{94}\text{<span style="font-weight: normal;font-style: normal;">Zr</span>}\right)-m\left({}^{140}\text{<span style="font-weight: normal;font-style: normal;">Ce</span>}\right)-m\left({}^1\text{<span style="font-weight: normal;font-style: normal;">n</span>}\right)\right]c^2=208\mathrm{,}7\text{<span style="font-weight: normal;font-style: normal;">MeV</span>}\mathrm{.}}\end{array}$ A.2. Az ${\text{<span style="font-weight: normal;font-style: normal;">U</span>}}_2\text{<span style="font-weight: normal;font-style: normal;">O</span>}$ (feladatban megadott) sűrűsége a térfogategységre eső molekulák össztömegét jelenti, így ezt elosztva a moláris tömeggel, majd megszorozva az $N_{\text{A}}$ Avogadro-állandóval, megkapjuk az 1 ${\text{<span style="font-weight: normal;font-style: normal;">m</span>}}^3$-nyi anyagban található ${\text{<span style="font-weight: normal;font-style: normal;">U</span>}}_2\text{<span style="font-weight: normal;font-style: normal;">O</span>}$-molekulák $N_1$ számát: $\begin{array}{c}{\displaystyle N_1=\frac{\varrho N_{\text{A}}}{M}=2\mathrm{,}364\cdot {10}^{28}{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}^{-3}\mathrm{.}}\end{array}$ Az urán-dioxid molekuláknak azonban csak $0\mathrm{,}72\%$-a tartalmazza a 235-ös uránizotópot, így a feladat kérdésére a válasz: $\begin{array}{c}{\displaystyle N=0\mathrm{,}0072\cdot N_1=1\mathrm{,}702\cdot {10}^{26}{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}^{-3}\mathrm{.}}\end{array}$ A.3. Az üzemanyagrúd egységnyi térfogatában $N$ hasadó uránatom van, ezek teljes hatáskeresztmetszete $N{\sigma }_f$. Ha ezt megszorozzuk a $\phi$ neutronfluxussal, az időegység alatt (köbméterenként) bekövetkező hasadások számát kapjuk: $\phi N{\sigma }_f$. Minden magreakcióban az A.1. részben kiszámolt $\Delta E$ energia szabadul fel, melynek $80\%$-a alakul hővé, így a hőfejlődés $Q$ üteme: $\begin{array}{c}{\displaystyle Q=0\mathrm{,}8\phi N{\sigma }_f\Delta E=4\mathrm{,}92\cdot {10}^8\text{<span style="font-weight: normal;font-style: normal;">W</span>}/{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}^3\mathrm{.}}\end{array}$ A.4. A $T_{\text{<span style="font-weight: normal;font-style: normal;">c</span>}}-T_{\text{<span style="font-weight: normal;font-style: normal;">s</span>}}$ hőmérsékletkülönbség $\text{<span style="font-weight: normal;font-style: normal;">K</span>}$ dimenziójú, így az $F\left(Q\mathrm{,}a\mathrm{,}\lambda \right)$ mennyiség mértékegysége is kelvin kell hogy legyen. Keressük az ismeretlen függvényt $F\left(Q\mathrm{,}a\mathrm{,}\lambda \right)=Q^{\alpha }{a}^{\beta }{\lambda }^{\gamma }$ alakban, és vizsgáljuk meg, mekkorának kell választanunk az $\alpha \mathrm{,}\beta \mathrm{,}\gamma$ számokat, hogy kelvin dimenziójú mennyiséget kapjunk. A jobb oldalon szereplő mennyiségek mértékegysége: $\begin{array}{c}{\displaystyle \left[Q\right]=\text{<span style="font-weight: normal;font-style: normal;">W</span>}{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}^{-3}=\text{<span style="font-weight: normal;font-style: normal;">kg</span>}{\text{<span style="font-weight: normal;font-style: normal;">s</span>}}^{-3}{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}^{-1}\mathrm{,}\left[a\right]=\text{<span style="font-weight: normal;font-style: normal;">m</span>}\mathrm{,}\left[\lambda \right]=\text{<span style="font-weight: normal;font-style: normal;">W</span>}{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}^{-1}{\text{<span style="font-weight: normal;font-style: normal;">K</span>}}^{-1}=\text{<span style="font-weight: normal;font-style: normal;">kg</span>}{\text{<span style="font-weight: normal;font-style: normal;">s</span>}}^{-3}\text{<span style="font-weight: normal;font-style: normal;">m</span>}{\text{<span style="font-weight: normal;font-style: normal;">K</span>}}^{-1}\mathrm{.}}\end{array}$ Ezek felhasználásával az alábbi egyenletet kapjuk a kitevőkre: $\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">K</span>}={\left(\text{<span style="font-weight: normal;font-style: normal;">kg</span>}{\text{<span style="font-weight: normal;font-style: normal;">s</span>}}^{-3}{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}^{-1}\right)}^{\alpha }{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}^{\beta }{\left(\text{<span style="font-weight: normal;font-style: normal;">kg</span>}{\text{<span style="font-weight: normal;font-style: normal;">s</span>}}^{-3}\text{<span style="font-weight: normal;font-style: normal;">m</span>}{\text{<span style="font-weight: normal;font-style: normal;">K</span>}}^{-1}\right)}^{\gamma }\mathrm{,}}\end{array}$ amiből $\alpha =1$, $\beta =2$, $\gamma =-1$ adódik. Tehát az üzemanyagrúd közepének és felületének hőmérsékletkülönbségét megadó formula (a feladatban megadott $1/4$-es faktort is visszaírva)2: $\begin{array}{c}{\displaystyle T_{\text{<span style="font-weight: normal;font-style: normal;">c</span>}}-T_{\text{<span style="font-weight: normal;font-style: normal;">s</span>}}=\frac{Q{a}^2}{4\lambda }\mathrm{.}}\end{array}$ A.5. Az üzemanyagrúd közepének a hőmérséklete nem érheti el az ${\text{<span style="font-weight: normal;font-style: normal;">U</span>}}_2\text{<span style="font-weight: normal;font-style: normal;">O</span>}$ olvadási hőmérsékletét, míg a külső felületének hőmérséklete a hűtőközeg hőmérsékletével egyezik meg. Így az A.4. részfeladatban kapott összefüggés szerint az üzemanyagrúd sugarának lehetséges legnagyobb $a_{\text{<span style="font-weight: normal;font-style: normal;">u</span>}}$ értéke $\begin{array}{c}{\displaystyle a_{\text{<span style="font-weight: normal;font-style: normal;">u</span>}}=\sqrt[]{\frac{4\lambda \left(T_{\text{<span style="font-weight: normal;font-style: normal;">c</span>}}-T_{\text{<span style="font-weight: normal;font-style: normal;">s</span>}}\right)}{Q}}\mathrm{,}}\end{array}$ ahol most $T_{\text{<span style="font-weight: normal;font-style: normal;">c</span>}}=T_{\text{<span style="font-weight: normal;font-style: normal;">olv</span>}}=3138\text{<span style="font-weight: normal;font-style: normal;">K</span>}$, $T_{\text{<span style="font-weight: normal;font-style: normal;">s</span>}}=577\text{<span style="font-weight: normal;font-style: normal;">K</span>}$. A megadott adatokat és $Q$ fentebb kiszámolt értékét behelyettesítve $a_{\text{<span style="font-weight: normal;font-style: normal;">u</span>}}=8\mathrm{,}27\cdot {10}^{-3}\text{<span style="font-weight: normal;font-style: normal;">m</span>}$.   B rész. 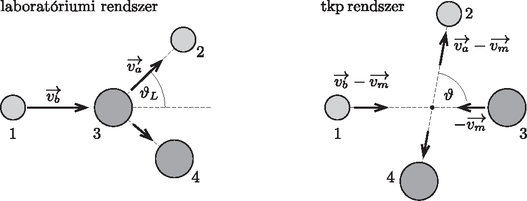A moderátor B.1. Az ábrán láthatóak a sebességviszonyok a tömegközépponti koordináta-rendszerben. Fontos megjegyezni, hogy a $\vartheta$ szög nagyobb, mint ${\vartheta }_L$.     B.2. A tömegközéppont sebessége a rendszer impulzusának és a teljes tömegének hányadosa: $\begin{array}{c}{\displaystyle v_m=\frac{v_b}{A+1}\mathrm{.}}\end{array}$ Ugyanekkora sebességgel mozog a tkp rendszerből nézve a laboratóriumi rendszerben kezdetben álló moderátoratom is: $\begin{array}{c}{\displaystyle V=\frac{v_b}{A+1}\mathrm{.}}\end{array}$ A neutron sebességének nagysága az ütközés előtt a tkp rendszerben: $\begin{array}{c}{\displaystyle v=v_b-v_m=\frac{A}{A+1}{v}_b\mathrm{.}}\end{array}$ A tkp rendszerben a rugalmas ütközés során az energia- és impulzusmegmaradás úgy teljesül, hogy a neutron és a moderátoratom is megőrzi az ütközés előtti sebességének nagyságát (rendre $v$ és $V$), csupán a sebesség iránya változik meg. B.3. Ütközés után a neutron sebességvektora a laboratóriumi rendszerben $\overrightarrow{v_a}=\overrightarrow{v}+\overrightarrow{v_m}$, így a sebességnégyzetének nagysága (a vektorháromszögben felírható koszinusztételből): $\begin{array}{c}{\displaystyle v_a^2=v^2+v_m^2+2v{v}_m\text{cos}\vartheta \mathrm{.}}\end{array}$ Behelyettesítve $v$ és $v_m$ előző részfeladatban kiszámolt értékét: $\begin{array}{c}{\displaystyle v_a^2=\frac{A^2{v}_b^2}{{\left(A+1\right)}^2}+\frac{v_b^2}{{\left(A+1\right)}^2}+\frac{2A{v}_b^2}{{\left(A+1\right)}^2}\text{cos}\vartheta \mathrm{,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle G\left(\alpha \mathrm{,}\vartheta \right)=\frac{E_a}{E_b}=\frac{v_a^2}{v_b^2}=\frac{A^2+2A\text{cos}\vartheta +1}{{\left(A+1\right)}^2}\mathrm{.}}\end{array}$ Ez kis átalakítással felírható $\alpha$ segítségével is: $\begin{array}{c}{\displaystyle G\left(\alpha \mathrm{,}\vartheta \right)=\frac{A^2+1}{{\left(A+1\right)}^2}+\frac{2A}{{\left(A+1\right)}^2}\text{cos}\vartheta =\frac{1}{2}\left[\left(1+\alpha \right)+\left(1-\alpha \right)\text{cos}\vartheta \right]\mathrm{.}}\end{array}$ B.4. Az energiaveszteség akkor a legnagyobb, ha a $G\left(\alpha \mathrm{,}\vartheta \right)$ mennyiség a lehető legkisebb. Ez (akár intuícióval, akár az előző részben kapott kifejezést vizsgálva) akkor következik be, ha $\vartheta ={180}^{\circ }=\pi$, azaz ha az ütközés lineáris. Ekkor $G\left(\alpha \mathrm{,}\pi \right)=\alpha$, a legnagyobb relatív energiaveszteség pedig $\begin{array}{c}{\displaystyle f_l={\left(\frac{E_b-E_a}{E_b}\right)}_{\underset{}{\overset{}{\text{max}}}}=1-G\left(\alpha \mathrm{,}\pi \right)=1-\alpha \mathrm{.}}\end{array}$ Most $\alpha ={\left(19/21\right)}^2$, így $f_l\approx 0\mathrm{,}181$.   C rész. A nukleáris reaktor C.1. A reaktor térfogata adott: $V=\pi R^{2}H$. Kérdés, hogyan kell megválasztani az $R:H$ arányt, hogy az elszökő neutronfluxusban szereplő $\begin{array}{c}{\displaystyle x={\left(\frac{2\mathrm{,}405}{R}\right)}^2+{\left(\frac{\pi }{H}\right)}^2}\end{array}$ kifejezés minimális legyen. Fejezzük ki $R^2$ értékét a térfogattal: $\begin{array}{c}{\displaystyle x=\frac{2\mathrm{,}{405}^2\pi H}{V}+{\left(\frac{\pi }{H}\right)}^2\mathrm{.}}\end{array}$ Bontsuk az első tagot két egyenlő kifejezés összegére, majd alkalmazzuk a számtani és mértani közepek között fennálló egyenlőtlenséget: $\begin{array}{c}{\displaystyle x=\frac{2\mathrm{,}{405}^2\pi H}{2V}+\frac{2\mathrm{,}{405}^2\pi H}{2V}+\frac{{\pi }^2}{H^2}\ge \sqrt[3]{\frac{2\mathrm{,}{405}^2\pi H}{2V}\cdot \frac{2\mathrm{,}{405}^2\pi H}{2V}\cdot \frac{{\pi }^2}{H^2}}\mathrm{.}}\end{array}$ A jobb oldalon láthatóan kiesik $H$, így egy konstans értéket kapunk. Ezt a bal oldali kifejezés akkor veszi fel, ha a benne szereplő három tag értéke megegyezik, azaz $\begin{array}{c}{\displaystyle \frac{2\mathrm{,}{405}^2}{2R^2}=\frac{{\pi }^2}{H^2}\mathrm{,}\text{<span style="font-weight: normal;font-style: normal;">valamint</span>}x=\frac{3{\pi }^2}{H^2}\mathrm{.}}\end{array}$ Használjuk még fel, hogy stacionárius állapotban az időegység alatt kiszökő és a láncreakcióban termelődő (többlet)neutronok száma megegyezik, vagyis $k_{1}x\psi =k_2\psi \mathrm{,}$ amiből $\begin{array}{c}{\displaystyle H=\sqrt[]{\frac{3{\pi }^2}{x}}=\sqrt[]{\frac{3{\pi }^2{k}_1}{k_2}}\approx 5\mathrm{,}87\text{<span style="font-weight: normal;font-style: normal;">m</span>}\mathrm{,}\text{<span style="font-weight: normal;font-style: normal;">és</span>}R=\frac{2\mathrm{,}405H}{\sqrt[]{2}\pi }\approx 3\mathrm{,}175\text{<span style="font-weight: normal;font-style: normal;">m</span>}\mathrm{.}}\end{array}$ C.2. A $d=0\mathrm{,}287\text{<span style="font-weight: normal;font-style: normal;">m</span>}$ oldalélű négyzetrácsba rendezett üzemanyag-kazetták mindegyikére $d^2$ nagyságú keresztmetszet-terület jut a reaktorban. Mivel a reaktor teljes keresztmetszete $\pi R^2$ (ahol $R$ az előző feladatrészben meghatározott érték), így a reaktorban elférő kazetták száma legfeljebb $\begin{array}{c}{\displaystyle F_n=\frac{\pi R^2}{d^2}\approx 387.}\end{array}$ Egyetlen (henger alakú) fűtőkazetta térfogata $\pi r_{\text{<span style="font-weight: normal;font-style: normal;">kazetta</span>}}H$ (ahol $r_{\text{<span style="font-weight: normal;font-style: normal;">kazetta</span>}}=3\mathrm{,}617\cdot {10}^{-2}\text{<span style="font-weight: normal;font-style: normal;">m</span>}$), sűrűsége adott ($\varrho =1\mathrm{,}060\text{<span style="font-weight: normal;font-style: normal;">kg</span>}{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}^{-3}$), így a fűtőelemek össztömege $\begin{array}{c}{\displaystyle M=F_n\pi r_{\text{<span style="font-weight: normal;font-style: normal;">kazetta</span>}}H\varrho \approx 9\mathrm{,}90\cdot {10}^4\text{<span style="font-weight: normal;font-style: normal;">kg</span>}\mathrm{.}}\end{array}$   Kísérleti feladatok A Fény Nemzetközi Évéhez igazodva a kísérleti fordulóban optikai mérési feladatok voltak. Mindkét mérésben fényelhajlás (diffrakció) segítségével kellett tanulmányozni különböző struktúrákat, így a két feladathoz a (nagyon igényesen elkészített) mérési eszközök részben azonosak voltak. Emiatt a feladatokat csak meghatározott sorrendben lehetett elvégezni.   1. feladat: Diffrakció csavarvonal alakú szerkezeteken A DNS kettős spirál alakjának felfedezését egy, a DNS molekuláról készült röntgendiffrakciós kép alapozta meg. A mérési feladatban ehhez hasonlóan diffrakció segítségével kellett csavarvonal alakú szerkezetek geometriai paramétereit meghatározni. A mérési berendezés lézermodulból, mintatartóból, tükrökből (ezek segítségével a szűk helyen meghosszabbítható a fényút) és ernyőből állt, melyeket a mérés előtt gondosan be kellett állítani. A diffrakciós képen kialakuló kioltási helyek távolságát digitális tolómérővel lehetett leolvasni. A feladat első felében egy nagyon vékony huzalból készült, apró csavarrugó volt a vizsgálat tárgya. A meghatározandó mennyiségek: a csavarrugó $R$ sugara, $P$ menetemelkedése és a rugót alkotó drót $a$ átmérője. Merőleges irányból nézve a rugó vetülete egy cikkcakkvonal, amely egyenértékű két olyan, egymással $2\alpha$ szöget bezáró drótsorozattal, melyek párhuzamos helyzetű, egyforma vastagságú, egymástól $d$ távolságra lévő drótszakaszokból állnak. Az elmélet szerint egy $a$ átmérőjű huzalon kialakuló diffrakciós kép intenzitáseloszlása (a $\vartheta$ diffrakciós szög függvényében): $\begin{array}{c}{\displaystyle I\left(\vartheta \right)=I\left(0\right){\left(\frac{\text{sin}\beta }{\beta }\right)}^2\mathrm{,}\text{ahol}\beta =\frac{\pi a\text{sin}\vartheta }{\lambda }\mathrm{.}}\end{array}$ A középső folt ($\beta =\vartheta =0$) fényes, a többi olyan irányban, amelyre $\text{sin}\beta =0$ (de $\beta \ne 0$) az intenzitás zérus, kioltás lesz. Ez alapján az intenzitáseloszlás $n$-edik minimumának ${\vartheta }_n$ szöge: $\begin{array}{c}{\displaystyle \text{sin}{\vartheta }_n=\pm n\frac{\lambda }{a}\mathrm{,}n=\mathrm{1,2,3,}\text{...}\mathrm{.}}\end{array}$ Két párhuzamos, egymástól $d$ távolságra lévő, ugyanolyan vastag dróton kialakuló diffrakciós kép két mintázat kombinációja (az egyetlen dróton való elhajlás és a két drót között kialakuló interferencia miatt). A kialakuló intenzitáseloszlás: $\begin{array}{c}{\displaystyle I\left(\vartheta \right)=I\left(0\right)\text{cos}{}^2\delta {\left(\frac{\text{sin}\beta }{\beta }\right)}^2\mathrm{,}\text{ahol}\delta =\frac{\pi d\text{sin}\vartheta }{\lambda }\text{és}\beta =\frac{\pi a\text{sin}\vartheta }{\lambda }\mathrm{.}}\end{array}$ Az ernyőn a két, $2\alpha$ szöget bezáró drótsorozat két, $2\alpha$ szöget bezáró diffrakciós képet hozott létre, ebből $\alpha$ leolvasható volt. Mindkét diffrakciós képen megtalálhatóak voltak a drót átmérőjének és a drótok távolságának megfelelő kioltási helyek. Az előző összefüggés alapján is lehetett látni, hogy a diffrakciós képen a finom (apróbb) struktúrákhoz tartoznak a nagyobb távolságok és a durvább (nagyobb) méretekhez a kisebb távolságok. A leolvasott távolságokból grafikus ábrázolás és egyenesillesztés segítségével az $a$ drótátmérőt és a $d$ távolságot meg lehetett határozni, ezekből pedig a csavarvonal $R$ sugarát és $P$ menetemelkedését ki lehetett számítani. A (szabad szemmel alig látható) rugó drótátmérője $a=0\mathrm{,}15\text{mm}$, sugara $R=0\mathrm{,}75\text{mm}$, menetemelkedése $P=0\mathrm{,}9\text{mm}$ volt. A feladat második felében egy, a DNS kettős spirálját modellező síkbeli struktúrát kellett vizsgálni. Itt az előző rész két jellemző távolsága ($a$ és $d$) mellett egy harmadik (közepes) távolság is megjelenik, és így a diffrakciós képen is háromféle távolságot kellet felismerni és megmérni.   2. feladat: Diffrakció vízfelszínen kialakuló kapilláris hullámokon A folyadékok felszínén kialakuló és terjedő hullámok viselkedését két erő, a nehézségi erő és a felületi feszültségből származó erő határozza meg. Ha a hullámhossz kisebb egy ${\lambda }_{\text{kr}}$ kritikus hullámhossznál, akkor a nehézségi erő hatása elhanyagolható, ezek az ún. kapilláris hullámok. (${\lambda }_{\text{kr}}=2\pi \sqrt[]{\sigma /\rho g}$, ahol $\sigma$ a folyadék felületi feszültsége, $\rho$ a folyadék sűrűsége, $g$ pedig a nehézségi gyorsulás. A mérési feladatban kialakuló hullámok hullámhossza sokkal kisebb a kritikus hullámhossznál.) A kapillárishullámok a folyadék viszkozitása miatt csillapodnak. A mérési feladatban egy vízminta felületi feszültségét és viszkozitását kellett meghatározni a kapilláris hullámokon létrejövő fényelhajlás alapján. A kapilláris hullámok hullámhossza a fény hullámhosszához képest aránylag nagy, ezért jól mérhető diffrakcióhoz a fénynek lapos szögben kell esnie a folyadék felületére. (A diffrakciós maximumok távolságának mérése így is nehéz.) A feladat szövegében megadták a laposszögű diffrakció összefüggéseit: $\begin{array}{c}{\displaystyle k=\frac{2\pi }{{\lambda }_l}\text{sin}\vartheta \text{sin}\gamma \mathrm{,}}\end{array}$ ahol $k=2\pi /{\lambda }_f$ a kapilláris hullámok hullámszáma, ${\lambda }_l$ és ${\lambda }_f$ a lézerfény, illetve a felületi hullám hullámhossza, $\vartheta$ a lézerfény vízszintessel bezárt szöge és $\gamma$ a diffrakciós képen a központi maximum és az elsőrendű maximum közötti szögtávolság. A folyadék felszínén a kapilláris hullámokat egy $\omega =2\pi f$ körfrekvenciájú rezgéskeltő hozza létre. A hullám körfrekvenciájának és hullámszámának kapcsolata a diszperziós reláció: $\begin{array}{c}{\displaystyle \omega =\sqrt[]{\frac{\sigma }{\rho }{k}^q}\mathrm{,}}\end{array}$ ahol $q$ egy, a mérés során meghatározandó egész szám (elméleti értéke 3). A gondos beállítás és a fénysugár szögének megmérése után a különböző frekvenciájú hullámokat egy tablettel vezérelt rezgéskeltővel hozták létre a versenyzők. A diffrakciós maximumok távolságát az ernyő helyére szerelt digitális tolómérőhöz rögzített fotodetektorral mérték, ebből határozták meg a kapillárishullámok hullámszámát. Az $\text{ln}\omega$-$\text{ln}k$ grafikonból leolvasható a diszperziós relációban szereplő $q$ állandó és ($\rho$ ismeretében) a víz $\sigma$ felületi feszültsége. A feladat második felében a hullámok csillapítását kellett tanulmányozni. A hullámok $h$ amplitúdója a hullámkeltőtől $s$ távolságra: $h=h_0{e}^{-\delta s}$, ahol $h_0$ az amplitúdó a hullámkeltőnél, $\delta$ a csillapítási tényező. A tapasztalat szerint $h_0$ arányos a rezgéskeltőre kapcsolt feszültség effektív értékének $0\mathrm{,}4$-edik hatványával, a csillapítási tényező és a folyadék $\eta$ viszkozitásának kapcsolata: $\begin{array}{c}{\displaystyle \delta =\frac{8\pi \eta f}{3\sigma }\mathrm{.}}\end{array}$ A mérés során a versenyzők változtatták a hullámkeltő távolságát a fény beesési helyétől, és mérték, hogy a rezgéskeltőre mekkora feszültséget kell kapcsolni ahhoz, hogy a diffrakciós maximum intenzitása (amit a fotodetektor mér) állandó maradjon. A mérési adatokból ‐ megfelelő grafikon megrajzolásával és egyenesillesztéssel ‐ a vízminta viszkozitása meghatározható volt. 1Az elméleti feladatok szövegét a múlt havi számunkban közöltük. 2A dimenzióanalízis módszere egy dimenziótlan szorzótényező erejéig határozatlanul hagyja a megoldást. A helyzetet az tette volna egyértelművé, ha a feladat szövegében megadják, hogy a fizikai mennyiségek hatványainak szorzata előtt álló állandó számértéke éppen 1/4 (‐ a szerk.).