Cím:	Megoldásvázlatok a 2014/ sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Számadó László
Füzet:	2014/december, 521 - 526. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Mutassuk meg, hogy nincs olyan valós számpár, amelyre $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(x^2+5\right)}^2}& {\displaystyle =25-|y-3|}\hfill \\ \hfill {\displaystyle 21x+63y}& {\displaystyle =188}\hfill \end{array}}\}\mathrm{.}}\end{array}$ (11 pont)   Megoldás. Az első egyenletből: ${\left(x^2+5\right)}^2\ge 25$,  $25-|y-3|\le 25$. Így az első egyenlet megoldása csak $x=0$, $y=3$ lehet. Ezt a második egyenletbe behelyettesítve: $\begin{array}{c}{\displaystyle 21\cdot 0+63\cdot 3=189\ne 188.}\end{array}$ Az egyenletrendszernek tehát nincs megoldása.   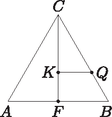2. Egy óra számlapja $20\text{cm}$ oldalhosszúságú szabályos háromszög. A mutatókat a háromszög középpontjában rögzítették úgy, hogy $12$ órakor az egyik csúcs felé mutatnak. $a)$ Milyen hosszú lehet a nagymutató, ha soha nem nyúlik túl az óra számlapján? $b)$ Három órakor a két mutató által meghatározott két félegyenes mekkora területű részt jelöl ki az óra számlapjából?  (12 pont)   Megoldás. $a)$ A nagymutató nem lehet hosszabb a 20 cm oldalhosszúságú szabályos háromszög beírt körének sugaránál. Mivel az $a$ oldalú szabályos háromszög területe: $t=\frac{a^2\sqrt[]{3}}{4}$, a kerülete: $k=3a$, most $t=100\sqrt[]{3}{\text{cm}}^2$, $k=60$ cm. A $t=rs$ ($r$ a beírt kör sugara, $s$ a kerület fele) összefüggés szerint: $\begin{array}{c}{\displaystyle r=\frac{100\sqrt[]{3}}{30}=\frac{10\sqrt[]{3}}{3}\mathrm{.}}\end{array}$ A nagymutató nem lehet hosszabb $\frac{10\sqrt[]{3}}{3}$ cm-nél.       $b)$ A mutatók által kijelölt $CKQ$ derékszögű háromszög hasonló a $CFB$ derékszögű háromszöghöz (a szögeik páronként egyenlők). Az $ABC$ szabályos háromszögben a $K$ pont egyben a súlypont is, így $CK:CF=2:3$. Ez lesz a két háromszög hasonlóságának aránya is. Tudjuk, hogy a területek a hasonlóság arányának négyzetével arányosak, ezért $\begin{array}{c}{\displaystyle t_{CKQ}={\left(\frac{2}{3}\right)}^2\cdot t_{CFB}=\frac{4}{9}\cdot \frac{1}{2}\cdot \frac{a^2\sqrt[]{3}}{4}=\frac{200\sqrt[]{3}}{9}\approx 38\mathrm{,}5{\text{(cm}}^2)\mathrm{.}}\end{array}$ Három órakor a két mutató által meghatározott két félegyenes 38,5 ${\text{cm}}^2$ területű részt jelöl ki az óra számlapjából.   3. Egy egyfordulós röplabdakupán ‐ ahol tehát bármely két csapat pontosan egyszer játszik egymással ‐ $30$ lejátszott mérkőzés után még minden csapatnak három mérkőzése volt hátra. Hány csapat szerepelt a kupán?  (14 pont)   Megoldás. Legyen a csapatok száma $n$. Az összes mérkőzések száma: $\frac{n\left(n-1\right)}{2}$. Minden csapatnak még 3 mérkőzése volt hátra, ez összesen $\frac{3n}{2}$ mérkőzés. Ezért a lejátszott mérkőzések száma: $\begin{array}{c}{\displaystyle \frac{n\left(n-1\right)}{2}-\frac{3n}{2}=\mathrm{30,}}\end{array}$ amiből az $n^2-4n-60=0$ másodfokú egyenletet kapjuk. A gyökök: $n_1=10$, $n_2=-6$. A röplabdakupán 10 csapat vett részt.   4. Határozzuk meg az $A\cap B$ halmazt, ha $A=\{x\in \text{R}\mid 3\left(\text{ctg}x-\text{tg}x\right)=2\sqrt[]{3}\}$, $B=\left\{x\in \text{R}\mid |x|\le 2\right\}$.  (14 pont)   Megoldás. Megoldjuk a $3\left(\text{ctg}x-\text{tg}x\right)=2\sqrt[]{3}$ egyenletet. Ez $\begin{array}{c}{\displaystyle 3\text{tg}{}^{2}x+2\sqrt[]{3}\text{tg}x-3=0}\end{array}$ alakra rendezhető, amiből $\text{tg}x$ lehetséges értékei: $\frac{\sqrt[]{3}}{3}$ vagy $-\sqrt[]{3}$. Vagyis $\begin{array}{c}{\displaystyle x_1=\frac{\pi }{6}+k_1\pi \mathrm{,}{x}_2=-\frac{\pi }{3}+k_2\pi \mathrm{,}\text{ahol}{k}_1\mathrm{,}{k}_2\in \text{Z}\mathrm{.}}\end{array}$ Az $|x|\le 2$ feltétel szerint $-2\le x\le 2$. Vagyis $\begin{array}{c}{\displaystyle A\cap B=\left\{-\frac{\pi }{3};\frac{\pi }{6}\right\}\mathrm{.}}\end{array}$   II. rész   5. A ${10}^n+{14}^n+{15}^n+{21}^n$ kifejezésben az $n$  $3$-mal osztható pozitív páratlan egész számot jelöl. $a)$ Igazoljuk, hogy a négytagú összeg minden ilyen $n$ esetén osztható lesz $1260$-nal. $b)$ A négytagú összeg két tagját véletlenszerűen kiválasztjuk. Mekkora valószínűséggel lesz a két tag összege hárommal osztható?  (16 pont)   Megoldás. $a)$ Alakítsuk át a négytagú kifejezést: $\begin{array}{c}{\displaystyle {10}^n+{14}^n+{15}^n+{21}^n=2^n\cdot 5^n+2^n\cdot 7^n+3^n\cdot 5^n+3^n\cdot 7^n=\left(2^n+3^n\right)\left(5^n+7^n\right)\mathrm{.}}\end{array}$ Legyen $n=3k$, ahol $k$ páratlan pozitív egész számot jelöl. Ekkor $\begin{array}{c}{\displaystyle \left(2^n+3^n\right)\left(5^n+7^n\right)=\left(2^{3k}+3^{3k}\right)\left(5^{3k}+7^{3k}\right)=\left(8^k+{27}^k\right)\left({125}^k+{343}^k\right)\mathrm{.}}\end{array}$ Mivel a kitevők páratlan számok, azért $35\mid 8^k+{27}^k$ és $468\mid {125}^k+{343}^k$. A 468 osztható 36-tal, és $\left(35;36\right)=1$, ezért a kifejezés osztható $35\cdot 36=1260$-nal. $b)$ A négytagú összeg két tagját hatféleképpen választhatjuk ki. Mivel a kitevők páratlan számok, azért az összeg osztható lesz az alapok összegével. Az alapok összege a következő hat érték közül kerülhet ki: 24, 25, 31, 29, 35, 36. Ezek közül két szám osztható hárommal, vagyis két esetben biztosan 3-mal osztható az összeg. A további négy esetben nem kaphatunk 3-mal osztható számot, mert a kéttagú összeg egyik tagja osztható 3-mal, a másik pedig nem. Így a keresett valószínűség $\frac{1}{3}$.   6. Egy háromszögben ismerjük mindhárom oldal hosszát és mindhárom szög nagyságát. Mutassuk meg, hogy ezeket az értékeket az $\begin{array}{c}{\displaystyle \frac{(\frac{a}{2}{)}^2+(\frac{b}{2}{)}^2+(\frac{c}{2}{)}^2}{\text{ctg}\alpha +\text{ctg}\beta +\text{ctg}\gamma }}\end{array}$ képletbe behelyettesítve a háromszög területét kapjuk.  (16 pont)   Megoldás. A megadott képletet alakítsuk a következő módon: $\begin{array}{c}{\displaystyle \frac{(\frac{a}{2}{)}^2+(\frac{b}{2}{)}^2+(\frac{c}{2}{)}^2}{\text{ctg}\alpha +\text{ctg}\beta +\text{ctg}\gamma }=\frac{a^2+b^2+c^2}{4\cdot (\frac{\text{cos}\alpha }{\text{sin}\alpha }+\frac{\text{cos}\beta }{\text{sin}\beta }+\frac{\text{cos}\gamma }{\text{sin}\gamma })}\mathrm{.}}\end{array}$ A koszinusz-tételt alkalmazva: $\text{cos}\alpha =\frac{b^2+c^2-a^2}{2bc}$. Ugyanígy felírhatjuk $\text{cos}\beta$ és $\text{cos}\gamma$ értékét is: $\begin{array}{c}{\displaystyle \text{cos}\beta =\frac{a^2+c^2-b^2}{2ac}\mathrm{,}\text{cos}\gamma =\frac{a^2+b^2-c^2}{2ab}\mathrm{.}}\end{array}$ Vagyis: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{a^2+b^2+c^2}{4\cdot (\frac{\text{cos}\alpha }{\text{sin}\alpha }+\frac{\text{cos}\beta }{\text{sin}\beta }+\frac{\text{cos}\gamma }{\text{sin}\gamma })}=\frac{a^2+b^2+c^2}{4\cdot \left(\frac{\frac{b^2+c^2-a^2}{2bc}}{\text{sin}\alpha }+\frac{\frac{a^2+c^2-b^2}{2ac}}{\text{sin}\beta }+\frac{\frac{a^2+b^2-c^2}{2ab}}{\text{sin}\gamma }\right)}=}\hfill \\ \hfill {\displaystyle =\frac{a^2+b^2+c^2}{4\cdot (\frac{b^2+c^2-a^2}{2bc\text{sin}\alpha }+\frac{a^2+c^2-b^2}{2ac\text{sin}\beta }+\frac{a^2+b^2-c^2}{2ab\text{sin}\gamma })}=\frac{a^2+b^2+c^2}{4\cdot (\frac{b^2+c^2-a^2}{4t}+\frac{a^2+c^2-b^2}{4t}+\frac{a^2+b^2-c^2}{4t})}=}\hfill \\ \hfill {\displaystyle =\frac{t\left(a^2+b^2+c^2\right)}{\left(b^2+c^2-a^2\right)+\left(a^2+c^2-b^2\right)+\left(a^2+b^2-c^2\right)}=\frac{t\left(a^2+b^2+c^2\right)}{a^2+b^2+c^2}=t\mathrm{.}}\hfill \end{array}}$ Valóban a háromszög területét adja ez a képlet.   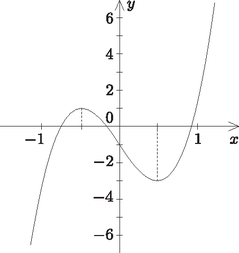7. Igazoljuk, hogy a valós számok halmazán értelmezett $f\left(x\right)=8x^3-6x-1$ hozzárendeléssel megadott függvénynek három különböző zérushelye van és ezek közül a legnagyobb: $x_1=\text{cos}\frac{\pi }{9}$.  (16 pont)   Megoldás. Tudjuk, hogy $f\left(x\right)$ mindenütt folytonos függvény. Mivel az $\begin{array}{c}{\displaystyle f\text{'}\left(x\right)=24x^2-6}\end{array}$ függvény zérushelyei a $-\frac{1}{2}$ és az $\frac{1}{2}$, azért itt lehet az eredeti függvénynek lokális szélsőértéke. Ezeken a helyeken az első derivált előjelet vált (pozitívból negatívba, illetve negatívból pozitívba megy át), így az első helyen lokális maximuma, a második helyen lokális minimuma van a függvénynek. Számolással kapjuk, hogy $f\left(-0\mathrm{,}5\right)=1$ és $f\left(0\mathrm{,}5\right)=-3$. Vagyis a $\left]-\frac{1}{2};\frac{1}{2}\right[$ intervallumon van zérushelye a függvénynek. ${\displaystyle \begin{array}{|cccccc|}\hline \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false"><</mo><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></mrow><mo stretchy="false"><</mo><mi>x</mi><mo stretchy="false"><</mo><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">=</mo><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mspace backround="\#000" height="12pt" depth="6pt" width="0pt"></mspace></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></mrow><mo stretchy="false"><</mo><mi>x</mi></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>↗</mo></math>}}\hfill & \hfill {\displaystyle \text{maximum}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>↘</mo></math>}}\hfill & \hfill {\displaystyle \text{minimum}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>↗</mo></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mo stretchy="false">'</mo></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">+</mo></math>}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo></math>}}\hfill & \hfill {\displaystyle \text{0}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">+</mo></math>}}\hfill \\ \hline\end{array}}$     Mivel $\underset{x\to \infty }{\overset{}{\text{lim}}}\left(8x^3-6x-1\right)=\infty$, azért az $\left]\frac{1}{2};\infty \right[$ intervallumon is van zérushelye a függvénynek. Mivel $\underset{x\to -\infty }{\overset{}{\text{lim}}}\left(8x^3-6x-1\right)=-\infty$, azért a $\left]-\infty ;-\frac{1}{2}\right[$ intervallumon is van zérushelye a függvénynek. Azaz van három különböző zérushelye. Mivel $f\left(0\right)=-1$, azért a középső zérushelyről az is megállapítható, hogy a $\left]-\frac{1}{2};0\right[$ intervallumon található. Ez azt jelenti, hogy két negatív és egy pozitív zérushellyel rendelkezik a függvény. Tudjuk, hogy $\text{cos}\frac{\pi }{9}>0$, ezért ha az $x_1=\text{cos}\frac{\pi }{9}$ valóban zérushelye a függvénynek, akkor az a három zérushely közül csakis a legnagyobb lehet. A $\frac{\pi }{9}$ háromszorosa $\frac{\pi }{3}$, ami nevezetes szög. Tudjuk, hogy $\text{cos}\frac{\pi }{3}=\frac{1}{2}$. Alkalmazzuk a $\text{cos}3\alpha =4\text{cos}{}^3\alpha -3\text{cos}\alpha$ összefüggést: $\begin{array}{c}{\displaystyle \text{cos}\frac{\pi }{3}=4\text{cos}{}^3\frac{\pi }{9}-3\text{cos}\frac{\pi }{9}\mathrm{.}}\end{array}$ Ezt 2-vel szorozva és rendezve kapjuk: $\begin{array}{c}{\displaystyle 8\text{cos}{}^3\frac{\pi }{9}-6\text{cos}\frac{\pi }{9}-1=0.}\end{array}$ Ez pontosan azt jelenti, hogy az $f\left(x\right)=8x^3-6x-1$ hozzárendelésű függvénynek az $x_1=\text{cos}\frac{\pi }{9}$ a zérushelye.   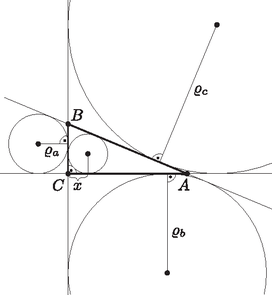8. Egy derékszögű háromszög beírt körének sugara $2$, a befogókhoz hozzáírt köreinek sugara $3$ és $10$. Mekkora az átfogóhoz hozzáírt kör sugara?  (16 pont)   Megoldás. Ha elkészítjük az ábrát (és a szokásos jelöléseket használjuk), akkor könnyen igazolható, hogy ${\varrho }_a=s-b$ és ${\varrho }_b=s-a$. A két összefüggés összeadásával kapjuk, hogy ${\varrho }_a+{\varrho }_b=c$. A megadott adatok szerint: $c=13$.     Derékszögű háromszög esetén ${\varrho }_c=s$. Ha a háromszög beírt körének a $BC$ oldallal vett érintési pontja és a $B$ csúcs közti távolság $x$, akkor: ${\left(x+2\right)}^2+{\left(15-x\right)}^2=169$, amiből $x^2-13x+30=0$, $x_1=10$, $x_2=3$. Innen $a=5$, $b=12$. A derékszögű háromszög mindhárom oldalát ismerve az átfogóhoz hozzáírt kör sugarát kiszámolhatjuk: ${\varrho }_c=s=\frac{5+12+13}{2}=15$.   Megjegyzés. Általában is megmutathatjuk, hogy derékszögű háromszög esetén: ${\varrho }_a+{\varrho }_b+\varrho ={\varrho }_c$.   9. Egy pihenőpark használatáért az üzemeltető pénzt szeretne kapni, ezért két lehetőséget dolgoztatott ki. Az első változat szerint lenne $12$ órás és $6$ órás jegy. A $12$ órás jeggyel nyitástól zárásig bent lehet lenni 1000 Ft-ért, a $6$ órás jegy ára pedig 600 Ft lenne. A második változat szerint lenne $3$ órás jegy 350 Ft-ért, $6$ órás jegy 600 Ft-ért, $9$ órás jegy 850 Ft-ért és az ezt meghaladó időre szóló jegy 1250 Ft-ért. Megfigyeltek $150$ látogatót és a következő gyakoriság adódott:   ${\displaystyle \begin{array}{ccccccccccccc}{\displaystyle \text{időtartam (h)}}\hfill & {\displaystyle \text{0‐1}}\hfill & \hfill {\displaystyle \text{1‐2}}\hfill & \hfill {\displaystyle \text{2‐3}}\hfill & \hfill {\displaystyle \text{3‐4}}\hfill & \hfill {\displaystyle \text{4‐5}}\hfill & \hfill {\displaystyle \text{5‐6}}\hfill & \hfill {\displaystyle \text{6‐7}}\hfill & \hfill {\displaystyle \text{7‐8}}\hfill & \hfill {\displaystyle \text{8‐9}}\hfill & \hfill {\displaystyle \text{9‐10}}\hfill & \hfill {\displaystyle \text{10‐11}}\hfill & \hfill {\displaystyle \text{11‐12}}\hfill \\ {\displaystyle \text{gyakoriság (fő)}}\hfill & {\displaystyle \text{6}}\hfill & \hfill {\displaystyle \text{7}}\hfill & \hfill {\displaystyle \text{11}}\hfill & \hfill {\displaystyle \text{18}}\hfill & \hfill {\displaystyle \text{25}}\hfill & \hfill {\displaystyle \text{26}}\hfill & \hfill {\displaystyle \text{20}}\hfill & \hfill {\displaystyle \text{16}}\hfill & \hfill {\displaystyle \text{15}}\hfill & \hfill {\displaystyle \text{4}}\hfill & \hfill {\displaystyle \text{2}}\hfill & \hfill {\displaystyle \text{0}}\hfill \end{array}}$   $a)$ Mennyi lesz az adatok alapján az egy főre eső átlagos bevétel az első változat szerint? $b)$ Mennyi lesz az adatok alapján az egy főre eső átlagos bevétel a második változat szerint? $c)$ Egy harmadik változatban $4$, $8$ és $12$ órás jegyeket lehetne vásárolni, melyek ára arányos lenne az időtartammal. Milyen áron kellene adni ezeket a jegyeket, ha a rendelkezésre álló adatok alapján az egy főre eső átlagos bevételként 700 Ft körüli értéket szeretne kapni az üzemeltető és a jegyek ára $10$-zel osztható?  (16 pont)   Megoldás. $a)$ Az első változat szerint $20+16+15+4+2+0=57$ fő 1000 Ft-os jegyet, és $150-57=93$ fő 600 Ft-os jegyet vásárolna. Ekkor az egy főre eső átlagos bevétel: $\begin{array}{c}{\displaystyle \frac{57\cdot 1000+93\cdot 600}{150}=752\left(\frac{\text{Ft}}{\text{fő}}\right)\mathrm{.}}\end{array}$ $b)$ A második változat szerint $4+2+0=6$ fő 1250 Ft-os jegyet, $20+16+15=51$ fő 850 Ft-os jegyet, $18+25+26=69$ fő 600 Ft-os jegyet és $6+7+11=24$ fő 350 Ft-os jegyet vásárolna. Ekkor az egy főre eső átlagos bevétel: $\begin{array}{c}{\displaystyle \frac{24\cdot 350+69\cdot 600+51\cdot 850+6\cdot 1250}{150}=671\left(\frac{\text{Ft}}{\text{fő}}\right)\mathrm{.}}\end{array}$ $c)$ Legyen a 4 órás jegy ára $x$ Ft, ekkor a 8 órásé $2x$ Ft, a 12 órásé $3x$ Ft. A megadott adatok alapján $15+4+2+0=21$ fő $3x$ Ft-os jegyet, $25+26+20+16=87$ fő $2x$ Ft-os jegyet és $6+7+11+18=42$ fő $x$ Ft-os jegyet vásárolna. Ekkor az egy főre eső átlagos bevétel: $\begin{array}{c}{\displaystyle \frac{42\cdot x+87\cdot 2x+21\cdot 3x}{150}=\frac{279x}{150}\left(\frac{\text{Ft}}{\text{fő}}\right)\mathrm{.}}\end{array}$ Azt szeretnénk, hogy ez a szám 700 körüli érték legyen, vagyis $\frac{279x}{150}=700$, amiből $x\approx 376$. A jegyek ára kerekítés után lehetne: 380 Ft a 4 órásé, 760 Ft a 8 órásé és 1140 Ft a 12 órásé.