|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész
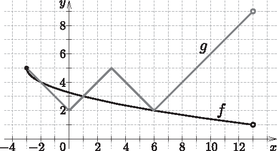
1. Ábrázoljuk derékszögű koordinátarendszerben az , függvényt.
Ábrázoljuk az előzővel azonos koordinátarendszerben a , függvényt.
Vizsgáljuk meg a függvényeket szélsőértékek szempontjából.
A függvényábrák segítségével oldjuk meg a következő egyenlőtlenséget: . (11 pont)
Megoldás. és A függvények képe az ábrán látható.
Az első esetben a függvény képét megrajzolva, majd a tanult transzformációkat alkalmazva jutottunk a megfelelő képhez: , , . A második esetben az függvény képét megrajzolva, majd a tanult transzformációkat alkalmazva jutottunk a megfelelő képhez: | |
Az függvény esetén abszolút maximumhely az . Az ehhez tartozó maximumérték az .
A függvény esetén lokális maximumhely az és az . Az ezekhez tartozó lokális maximumérték az .
A függvény esetén abszolút minimumhely az és az . Az ezekhez tartozó minimumérték az .
Az ábra alapján a () egyenlőtlenség megoldása: .
2. Tekintsük a következő öt állítást:
: Nem létezik olyan pozitív egészekből álló, öttagú számtani sorozat, amelyre igaz, hogy bármely két elemének a legnagyobb közös osztója .
: Ha egy síkbeli négyszög húrnégyszög, akkor létezik a síkjában egy olyan pont, amelytől a négyszög minden csúcsa azonos távolságra van.
: Egy elemű halmaz összes részhalmazainak száma .
: Ha egy egyenest 2014 db különböző sugarú kör ugyanabban az pontban érint, akkor e körök középpontjai egy egyenesre illeszkednek.
: Ha egy függvény periodikus, akkor képe szimmetrikus az tengelyre.
Állapítsuk meg, hogy melyik állítás igaz, és melyik állítás hamis. Indokoljuk válaszainkat.
Írjuk fel a és az állítások megfordítását, és állapítsuk meg az igazságértéküket.
Fogalmazzuk meg egy mondatban a állítást és a megfordítását. Igaz-e a kapott állítás?
Melyik a következő mondatok közül az állítás tagadása?
I. Ha egy függvény nem periodikus, akkor képe szimmetrikus az tengelyre.
II. Van olyan periodikus függvény, melynek képe nem szimmetrikus az tengelyre. (12 pont)
Megoldás. Az állítás hamis, ugyanis létezik olyan pozitív egészekből álló öttagú számtani sorozat, amelyre igaz, hogy bármely két elemének a legnagyobb közös osztója 1, például: 7; 13; 19; 25; 31.
A állítás igaz, hiszen ha egy síkbeli négyszög húrnégyszög, akkor definíció szerint létezik olyan körvonal, amely minden csúcsát tartalmazza. Ennek a körvonalnak a középpontja a húrnégyszög minden csúcsától azonos távolságra van.
A állítás hamis, hiszen egy elemű halmaz összes részhalmazainak száma: .
A állítás hamis. Amennyiben az állítás egy, az egyenest tartalmazó konkrét síkra vonatkozna, akkor igaz lenne, viszont az állítás szövegében semmi nem utal arra, hogy a köröknek egy síkban kellene elhelyezkedniük.
Az állítás hamis. Ellenpélda lehet például a szinusz függvény, amely periodikus, viszont nem páros, tehát képe nem szimmetrikus az tengelyre.
A állítás megfordítása: Ha egy síkbeli négyszög síkjában létezik egy olyan pont, amelytől a négyszög minden csúcsa azonos távolságra van, akkor a négyszög húrnégyszög. A állítás megfordítása igaz.
Az állítás megfordítása: Ha egy függvény képe szimmetrikus az tengelyre, akkor a függvény periodikus. Az állítás megfordítása hamis (nézzük például az függvényt).
A állításnak és a megfordításának egy mondatban történő megfogalmazása: Egy síkbeli négyszög akkor és csak akkor húrnégyszög, ha létezik a síkjában egy olyan pont, amelytől a négyszög minden csúcsa azonos távolságra van. Ez az állítás igaz.
Az állítás tagadása a II. mondat.
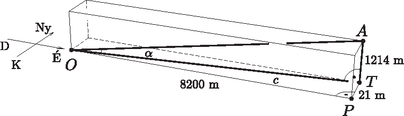
3. Egy magashegységben meteorológiai kutatóállomás működik. A tereptárgyak pontos helyét térbeli koordinátarendszerbeli koordinátahármasok segítségével tartják nyilván, melynek egységét minden tengelyen 1 méternek választották, és origójában van a kutatóállomás. A koordinátarendszer tengelye délről észak felé mutat, tengelye keletről nyugat felé irányul, tengelye pedig függőleges, és felfelé irányul. A pontok koordinátáit , , sorrendben adják meg. A környéken három meghatározó hegycsúcs van, melyek koordinátái: ; ; .
Melyik hegy van a kutatóállomástól megközelítőleg északi irányban? Milyen emelkedési szög alatt látja ennek a csúcsát a kutatóállomáson tartózkodó megfigyelő?
Mekkora az , és a hegycsúcsok tengerszint feletti magassága, ha a pont éppen a tengerszinten található?
A kutatóállomásról havonta helikopter indul. A személyzet feladata az , és a csúcsokon kihelyezett műszerekben az akkumulátorcsere. Mekkora utat tesz meg egy ilyen alkalommal a helikopter, ha a csúcsokat csúcs, csúcs, csúcs sorrendben járja be, majd visszatér a kutatóállomásra? (14 pont)
Megoldás. A kutatóállomástól az csúcs található közel északi irányban.
Az ábra jelöléseit használva (ahol jelöli a kutatóállomást), az derékszögű háromszögre felírva a Pitagorasz-tételt: . Az derékszögű háromszögre a tangens szögfüggvényt alkalmazva: | |
Vagyis az emelkedési szög kb. .
A tengerszint feletti magasságok: | |
c) A helikopter által megtett távolság:
dOA+dAB+dBC+dCO==82002+212+12142+(-28-8200)2+(7600-21)2+(1021-1214)2++(-1200+28)2+(-4550-7600)2+(900-1021)2++(-1200)2+(-4550)2+9002≈8289,41+11188,32+12206,99+4790,88==36475,60m.
4. a) Egy számtani sorozat második eleme 55-23, differenciája pedig 5+1. Mekkora az ötödik tag? Mennyi az első kilenc tag összege?
b) Ha egy számtani sorozat első tagjából levonunk kettőt, második tagjából levonunk egyet, és a harmadik tagjához hozzáadunk ötöt, akkor egy mértani sorozat első három elemét kapjuk. Melyik ez a számtani sorozat, ha tudjuk, hogy a kapott mértani sorozat első két elemének összege egyenlő az eredeti számtani sorozat harmadik tagjával?
c) Számítsuk ki a következő határértéket:
Megoldás. a) A sorozat ötödik tagja: | a5=a2+3⋅d=55-23+3⋅(5+1)=55-2+9⋅(5+1)3=145+73. |
Az első kilenc tag összege:
S9=a1+a2+a3+a4+a5+a6+a7+a8+a9==(a5-4d)+(a5-3d)+(a5-2d)+(a5-d)+a5++(a5+d)+(a5+2d)+(a5+3d)+(a5+4d)=9a5==9⋅145+73=425+21.
b) A számtani sorozat első három eleme: a1, a1+d, a1+2d. A mértani sorozat első három eleme: a1-2, a1+d-1, a1+2d+5. A mértani sorozat tulajdonsága alapján:
(a1+d-1)2=(a1-2)⋅(a1+2d+5),a12+d2+1+2a1d-2a1-2d=a12+2a1d+5a1-2a1-4d-10,d2+2d-5a1+11=0.
A szövegből tudjuk: a1-2+a1+d-1=a1+2d, a1=d+3. Ezt behelyettesítve az előző egyenletbe:
d2+2d-5(d+3)+11=d2-3d-4=0.
A másodfokú egyenlet két megoldása: d1=4, d2=-1. Ezek alapján az első tagra is két értéket kapunk: (a1)1=7, (a1)2=2. Az így kapott számtani sorozatok: 7, 11, 15, illetve 2, 1, 0.
Ellenőrzés után látható, hogy a feladat szövegének csak a 7, 11, 15 felel meg, ez az egyedüli megoldás.
limn→∞12n+1-n=limn→∞2n+1+n(2n+1-n)(2n+1+n)=(*)=limn→∞2n+1+nn+1=limn→∞2n+1n2+1n1+1n=0.
II. rész
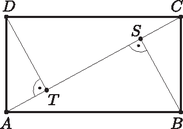
5. Az ábrán látható téglalap alakú csempéről tudjuk, hogy DTA∢=CSB∢=90∘, valamint AT=6cm, TS=14cm.
a) Mekkora egy ilyen csempe területe?
b) Hány db ilyen csempét kell rendelnünk egy 25 m alapkörsugarú, 2,5 m mély, henger alakú medence kicsempézéséhez, ha a vágások és a törések miatt 15%-os ráhagyás szükséges? (A csempéket csomagokban árusítják, de számításaink során ezzel ne foglalkozzunk.)
c) Hány fordulóval képes ezt egy 4 tonna teherbírású teherautó elhozni, ha egy csempe 5 mm vastag, és anyagának sűrűsége 2520kgm3?
d) Rendelkezésünkre áll egy olyan szivattyú, amely a 10 cm átmérőjű csövében a vizet 1ms sebességgel képes áramoltatni. Mennyi idő alatt tudja majd ez a szivattyú a színültig teletöltött medencét kiüríteni? (16 pont)
Megoldás. a) Szimmetriai tulajdonságok miatt: AT=SC(=6cm). Ebből adódik: TC=TS+SC=20 cm. Az ACD derékszögű háromszögre alkalmazva a magasságtételt: DT=AT⋅TC=6⋅20=120. Egy ilyen csempe területe: | 2⋅AC⋅TD2=26⋅120≈284,82(cm2)=0,028482(m2). |
b) A medence méretei: r=25 m, m=2,5 m. A csempézendő felszín: | A=r2⋅π+2⋅r⋅π⋅m=252⋅π+2⋅25⋅π⋅2,5=750⋅π≈2356,19(m2). |
A 15%-os ráhagyás miatt a szükséges csempemennyiség: T=2356,19⋅1,15≈2709,62(m2). Mivel 2709,62:0,028482≈95134, ezért kb. 95 134 db csempét kell rendelni.
c) A csempe vastagsága: d=5mm=0,005m. A csempék össztérfogata: | V=T⋅d=2709,62⋅0,005=13,5481(m3). |
A csempe sűrűsége: ϱ=2520kgm3. A csempék össztömege: | ϱ⋅V=2520⋅13,5481=34141,212(kg). |
Ez azt jelenti, hogy a 4 tonna teherbírású autónak 9 fordulóra lesz szüksége.
d) A medence térfogata: V=r2⋅π⋅m=252⋅π⋅2,5≈4908,74(m3). A szivattyú másodpercenként egy henger alakú, 5 cm sugarú és 1 m magas vízoszlopot képes kiemelni, ez 0,052⋅π⋅1=0,00785(m3) térfogatnak felel meg. A medence vízének kiemelése ezzel a szivattyúval | 4908,74:0,00785≈625317s≈173,7h≈7,24 |
napig tartana.
6. a) Egy osztályba 16 fiú és 14 leány jár. Egy alkalommal 11 egyforma könyvet sorsolnak ki köztük úgy, hogy egy tanuló csak egy könyvet kaphat. Mennyi a valószínűsége, hogy fiú is és lány is lesz a nyertesek között?
b) Egy középiskolai menzán az ebédhez süteményt lehet választani. Kétféle sütemény van, édes és sós. A tapasztalatok szerint annak valószínűsége, hogy egy diák édes süteményt választ 0,75. Mennyi annak a valószínűsége, hogy négy egymás után következő diákra nem lesz igaz, hogy azonos típusú süteményt választanak, ha mindegyikük pontosan egy süteményt visz magával?
c) Egy harminc fős alsó tagozatos osztályban van egy ikerpár. A tanító néni egy játékhoz véletlenszerűen két 15 fős csapatba fogja őket sorsolni. Mennyi a valószínűsége annak, hogy az ikerpár két tagja nem azonos csapatba kerül? (16 pont)
Megoldás. a) A könyvek kisorsolása (3011) féle eredménnyel végződhet. (1611)-féleképpen fordulhat elő, hogy csak fiú nyer könyvet, és (1411)-féleképpen állhat a nyertesek csoportja csupa leánytanulóból. Az előzőekből adódik, hogy (3011)-(1611)-(1411)-féleképpen fordulhat elő, hogy fiú is és lány is van a nyertesek között. A keresett valószínűség: | P=kedvező esetek számaösszes eset száma=(3011)-(1611)-(1411)(3011)≈0,99991. |
b) Legyen A esemény az, hogy négy egymást követő diák mindegyike édes süteményt választ, és B esemény az, hogy négy egymást követő diák mindegyike sós süteményt választ. Annak valószínűsége, hogy négy egymást követő diák mindegyike édes süteményt választ: P(A)=0,754=0,31640625. Annak valószínűsége, hogy négy egymást követő diák mindegyike sós süteményt választ: P(B)=0,254=0,00390625.
A feladat annak valószínűségét kérdezi, hogy az A és a B esemény egyike sem következik be. Mivel A és B egymást kizáró események, ez a következőképpen számolható: P=1-P(A)-P(B)=0,6796875.
c) Tegyük fel, hogy lezajlott a véletlenszerű sorsolás, de mi nem ismerjük az eredményt. Ekkor egy tetszőlegesen kiválasztott A tanulóra igaz, hogy 14 csapattársa és 15 ellenfele van. Ha most véletlenszerűen kiválasztunk egy B tanulót, akkor annak valószínűsége, hogy nem csapattársak 1529, hiszen B ilyen valószínűséggel lehet a másik csapat 15 embere közül valamelyik.
Tehát bármely két tanulót kiemelve 1529 a valószínűsége, hogy nincsenek egy csapatban. Ez az ikerpárra is igaz, tehát a keresett valószínűség: P=1529.
7. a) Igazoljuk, hogy a 22n-1 minden pozitív egész n számra osztható hárommal.
b) Igazoljuk, hogy a n-n36 kifejezés bármely n egész szám behelyettesítése esetén egész számot ad eredményül.
c) Hány pozitív osztója van a 201411⋅112014 számnak?
d) Négyzetszám-e a 32014-1? (16 pont)
Megoldás. a) Az a2-b2=(a+b)⋅(a-b) azonosságot alkalmazva a 22n-1 kifejezés (ahol n pozitív egész szám) átalakítható: 22n-1=(2n-1)⋅(2n+1).
Mivel (2n-1), 2n, (2n+1) három egymást követő pozitív egész szám, ezért valamelyik osztható hárommal. Mivel 2n biztosan nem osztható hárommal, ezért a 2n-1 és a 2n+1 közül az egyik lesz a három többszöröse. Ez pedig azt jelenti, hogy a (2n-1)⋅(2n+1) szorzat, azaz a 22n-1 biztosan osztható hárommal, ha n pozitív egész szám.
b) Alakítsuk át az n-n36 kifejezést, ahol n egész szám:
n-n36=n⋅(1-n2)6=n⋅(1-n)⋅(1+n)6=-n⋅(n-1)⋅(n+1)6==-(n-1)⋅n⋅(n+1)6.
A számlálóban három egymást követő egész szám szorzata van, amiről tudjuk, hogy osztható hattal. (Biztos van köztük kettővel osztható szám, valamint biztos van köztük hárommal osztható szám.) Ez azt jelenti, hogy a -(n-1)⋅n⋅(n+1)6, azaz az n-n36 egész szám minden egész n esetén.
c) Egy szám pozitív osztói számának meghatározásához szükség van a szám prímtényezős felbontására: 201411⋅112014=211⋅1911⋅5311⋅112014. Vagyis a 201411⋅112014 szám pozitív osztóinak száma: (11+1)⋅(11+1)⋅(11+1)⋅(2014+1)=3481920.
d) Használjuk fel azt az ismeretet, hogy egy egész szám négyzete hárommal osztva csak 0 vagy 1 maradékot adhat.
Mivel a 32014-1 érték eggyel kisebb egy hárommal osztható számnál, ezért hárommal osztva kettő maradékot ad, tehát nem lehet négyzetszám.
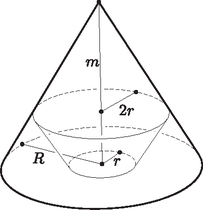
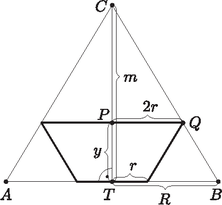
8. A képen látható R=30cm alapkörsugarú, és m=50cm magasságú egyenes kúpba egyenes csonkakúpokat írunk a következő feltételekkel:
‐ A csonkakúp kisebb alapkörének sugara a nagyobb alapköre sugarának felével egyenlő.
‐ A csonkakúp nagyobb alapkörének körvonala a kúp palástjára illeszkedik.
‐ A csonkakúp kisebb alapköre a kúp alapsíkjára illeszkedik.
a) Mennyi az ilyen csonkakúpok közül a maximális térfogatú magassága?
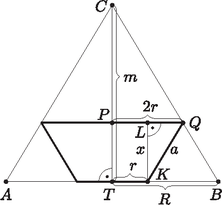
b) Mekkora a csonkakúp felszíne és térfogata, ha r=R3? (16 pont)
Megoldás.
a) Használjuk az ábra jelöléseit, ahol y-nal jelöltük a csonkakúp magasságát. Keressük azt az y értéket, amelyre a keletkezett csonkakúp térfogata maximális.
Alkalmazva a párhuzamos szelőszakaszok tételét, mivel PQ∥TB, ezért felírható: A csonkakúp térfogata:
V=((2r)2+(2r)⋅r+r2)⋅y⋅π3=((2r)2+(2r)⋅r+r2)⋅150-10r3⋅π3==7⋅r2⋅(150-10r)⋅π9=70⋅π9⋅(15r2-r3).
Keressük, hogy a térfogat milyen r értékre lesz maximális. Mivel a 70⋅π9 konstans, ezért elég megkeresni, hogy a 15r2-r3 kifejezés milyen r érték esetén maximális.
A kifejezés deriváltja: [15r2-r3]'=30r-3r2. A kifejezés csak olyan r helyen lehet maximális, ahol a derivált értéke 0, azaz 3r⋅(10-r)=0. Vagyis r=0 és r=10 esetén 0 a derivált. Mivel r=0 esetén nem keletkezik csonkakúp, ezért csak az r=10 esetén képzelhető el, hogy maximális lesz a térfogat.
A 15r2-r3 kifejezés második deriváltja: [15r2-r3]''=30-6r. A második derivált az r=10 esetén negatív, tehát a 15r2-r3 kifejezésnek r=10 esetén valóban maximuma van. Vagyis a keletkezett csonkakúp térfogata akkor lesz maximális, ha r=10 cm. Alkalmazva az y=150-10r3 összefüggést kapjuk: y=503 cm.
Tehát a maximális térfogatú csonkakúp magassága pontosan 503 cm.
b) Ismét az ábra jelöléseit használva alkalmazhatjuk a párhuzamos szelőszakaszok tételét. Mivel PQ∥TB, ezért felírható: m-x2r=mR. Tudjuk, hogy r=R3, ezért egyenletünk a következőképpen módosul: m-x2r=m3r, 3⋅(m-x)=2m, x=m3. Kaptuk, hogy a csonkakúp magassága x=503 cm, és mivel r=R3=303=10 cm, ezért a csonkakúp nagyobb alapkörének sugara 2r=20 cm, a kisebb alapkörének sugara pedig r=10 cm.
A csonkakúp térfogata:
V=((2r)2+(2r)⋅r+r2)⋅x⋅π3=(202+20⋅10+102)⋅503⋅π3=35000⋅π9≈≈12217,3(cm3).
A csonkakúp a alkotója a KLQ derékszögű háromszögből számolható Pitagorasz-tétel segítségével: a2=x2+r2=(503)2+102=34009, a=10343. A csonkakúp felszíne:
A=(2r)2⋅π+r2⋅π+(2r+r)⋅a⋅π=400⋅π+100⋅π+100⋅34⋅π≈3402,64(cm2).
9. a) Oldjuk meg a következő egyenletet: | sin4x+2cosx2cos4x+2=2(-sin2x-cos2x-1). |
b) Igazoljuk a következő egyenlőtlenséget: ahol a, b, c tetszőleges pozitív valós számok. (16 pont)
Megoldás. a) Az egyenlet bal oldalának nevezőjében található 2cos4x+2 kifejezés biztosan pozitív, tehát az egyenlet értelmezési tartománya a valós számok halmaza.
Az egyenlet jobb oldalán a sin2x+cos2x=1 összefüggést alkalmazva, és további átalakításokkal kapjuk: | sin4x+2cosx2cos4x+2=(2)-2=12, |
| sin4x+2cosx=cos4x+1,sin4x-cos4x=1-2cosx. |
Alkalmazva az a2-b2=(a+b)(a-b), valamint a sin2x+cos2x=1 összefüggéseket:
(sin2x-cos2x)(sin2x+cos2x)=1-2cosx,sin2x-cos2x=1-2cosx.
Újra alkalmazva a sin2x+cos2x=1 összefüggést: 1-2cos2x=1-2cosx. Rendezve a kapott egyenletet: cos2x-cosx=0, cosx(cosx-1)=0.
I. eset: Ha cosx=0, akkor x1=π2+k1π, ahol k1∈Z.
II. eset: cosx=1, akkor x2=2k2π, ahol k2∈Z.
b) A bizonyítandó egyenlőtlenség jobb oldalát átalakíthatjuk: | lg(a23bc+b23ac+c23ab)≥lg1. |
A logaritmusfüggvény szigorú monoton növekedése miatt: a23bc+b23ac+c23ab≥1. Mivel a, b, c tetszőleges pozitív valós számok, ezért ha az egyenlőtlenség mindkét oldalát megszorozzuk az abc kifejezéssel, akkor a következőt kapjuk: A kapott egyenlőtlenség igaz, hiszen ez az a3, b3, c3 pozitív számokra a számtani és a mértani közép közötti összefüggés.
A gondolatmenet során végig ekvivalens átalakításokat végeztünk, ezért az eredeti állítás is igaz. |
 PDF | MathML
PDF | MathML