|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A verseny időtartama 90 perc. A feladatok pontozása: minden helyes válasz 5 pontot ér; helytelen válaszra 0 pont, válasz nélkül hagyott kérdésekre 1-1 pontot jár.
1. Mennyi az szám normálalakjában a hatványkitevő? (A) ; (B) ; (C) ; (D) 0; (E) 1.
2. Hány olyan négyjegyű négyzetszám van, amelynek minden számjegye eleme a halmaznak? (A) 0; (B) 1; (C) 2; (D) 3; (E) 4.
3. Mennyi az összeg, ha ? (A) 1; (B) 2; (C) 3; (D) 4; (E) 5.
4. Egy síugró versenyen hatan indultak, minden versenyző egyszer ugrott. Az ugrásokat nevük ábécé sorrendjében hajtották végre. A versenyzők után álló szám azt jelenti, hogy az addigi ugrások közül hányadik a versenyző: András (1.), Béla (1.), Csaba (3.), Dani (3.), Elemér (2.), Ferenc (2.). Ki volt a verseny 3. helyezettje? (A) András; (B) Béla; (C) Csaba, (D) Dani; (E) Elemér
5. Melyik igaz? (A) ; (B) ;
(C) ; (D) ; (E) .
6. Hány köbszám van a alakú számok között, ha prímszám? (A) 0; (B) 1; (C) 3; (D) 4; (E) 5.
7. A 4; 6; 7 és 8 számjegyek felhasználásával 1024 különböző számot képezünk úgy, hogy közülük a legnagyobb szám a lehető legkisebb legyen. Hány jegyű az így képzett 1024 szám közül a legnagyobb? (A) 3; (B) 4; (C) 5; (D) 6; (E) 7.
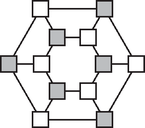
8. Az ábrán a Kacsaláb Lakópark rajza látható. A rajzon minden épületet négyzet, két szomszédos épületet összekötő gyalogutat vonal jelöl. Minden szürke színnel jelölt épületben annyi lakó lakik, amennyi a vele szomszédos épületekben összesen. (Két épület szomszédos, ha van közöttük közvetlen gyalogút.) Hány lakó nem lakhat a lakóparkban? (A) 24; (B) 28; (C) 32; (D) 36; (E) 42.
9. Hányféleképpen írható be egy -as négyzetrács kilenc négyzetébe a KESZTHELYEN szó, ha minden négyzetbe egy betűt írunk, az egymást követő betűk oldallal szomszédos négyzetekbe kerülnek, és nincs olyan sor vagy olyan oszlop, amelybe egynél több magánhangzó kerül? (Az elforgatással egymásba vihető megoldásokat nem tekintjük különbözőnek.) (A) 0; (B) 1; (C) 9; (D) 3240; (E) 6480.
10. Anna állítása szerint a 23; a 32 és a 41 három olyan egész szám, amely lehet egy derékszögű háromszög három oldalhosszának ‐ ugyanabban a mértékegységben vett ‐ mérőszáma. Milyen számrendszerben adta meg Anna az oldalhosszak mérőszámát? (A) 5; (B) 6; (C) 7; (D) 8; (E) 9.
11. Mennyi az összeg lehetséges legnagyobb értéke, ha , és három egymástól és 0-tól különböző egész szám? (A) ; (B) ; (C) 2,25; (D) 3; (E) Az előzőek közül egyik sem.
12. Jelölje egy téglalap kerületét , az átlóját ! Melyik igaz a téglalap területére vonatkozóan az alábbiak közül? (A) A terület biztosan egész szám.; (B) A terület nem lehet egész szám; (C) ; (D) ; (E) A terület nem egyértelműen meghatározott.
13. Mennyi a összeg? (A) 0; (B) ; (C) ; (D) ; (E) 1.
14. Legkevesebb hány pozitív osztója lehet egy olyan számnak, amely kétszeresének 15 pozitív osztója van? (A) 8; (B) 10; (C) 12; (D) 14; (E) 15.
15. Mennyi , ha és , ha , és természetes számok? (A) 91; (B) 107; (C) 1009; (D) 2013; (E) 2015.
16. Mennyi annak a valószínűsége, hogy egy olyan téglatest testátlója, melynek élei tetszőlegesen választott, egységnyi hosszúságnál rövidebb szakaszok, kisebb az egységnél? (A) 0,48; (B) 0,5; (C) ; (D) ; (E) .
17. Mennyivel egyenlő , ha ? (A) ; (B) ; (C) ; (D) ; (E) .
18. Rebeka a 2014-nél kisebb pozitív egész számok mindegyikére kiszámolta értékét. Ezután Balázs mindegyik kiszámolt érték mellé odaírta, hogy hány nullára végződik. Hány különböző számot írt le Balázs? (A) 380; (B) 402; (C) 403; (D) 501; (E) 502.
19. Mennyi a számjegyek összege a legkisebb olyan pozitív egész számban, melyre egy egész szám köbe és teljes négyzet? (A) 2; (B) 3; (C) 4; (D) 10; (E) 14.
20. Egy sorba egymás mellé egyforma méretű korongokból tornyokat építünk úgy, hogy bármely két egyforma magas torony közé teszünk legalább egy náluk magasabb tornyot. A legmagasabb torony 8, a legalacsonyabb pedig 1 korongból áll. Mennyi a legtöbb torony, amit így építhetünk? (A) 32; (B) 64; (C) 125; (D) 255; (E) végtelen sok.
21. Egy matematikaversenyen négy feladatot tűztek ki. A versenyen elindult 50 versenyző közül az első feladatot 43-an, a másodikat 34-en, a harmadikat 36-an, a negyediket pedig 37-en oldották meg. Hányan oldották meg a harmadik és a negyedik feladatot is, ha mind a négy feladatot senki sem oldotta meg? (A) 20; (B) 23; (C) 27; (D) 30; (E) Ezekből az adatokból nem lehet meghatározni.
22. Mennyi a különbség lehető legnagyobb értéke? (A) 0; (B) ; (C) ; (D) ; (E) .
23. Egy -as tábla mezői meg vannak számozva 1-től 9-ig. Minden mezőben egy-egy lámpa található. Egy lámpának két állása van: világít vagy nem világít. Kezdetben egyik sem világít. Egy-egy lépésben egy tetszőleges -es négyzet minden mezőjén lévő lámpának az állását megváltoztatjuk. Hányféle különböző állapotba kerülhet a -as tábla véges sok lépés után? (Két állapot különböző, ha van olyan mező, amelyik lámpájának állása a két állapotban különböző.) (A) 4; (B) 9; (C) 16; (D) 18; (E) 512.
24. Melyik állítás igaz, ha , és , ahol , , valós számok? (A) ; (B) ; (C) ; (D) ; (E) Az előzőek közül egyik sem.
25. Az paralelogramma oldalának -hoz közelebbi harmadoló pontja , oldalának felezőpontja , és oldalának -hoz legközelebb levő negyedelő pontja . Milyen arányú részekre osztja az szakasz a szakaszt? (A) ; (B) ; (C) ; (D) ; (E) .
26. Hány olyan legfeljebb 2014-jegyű pozitív egész szám van, amelynek prímtényezős felbontása alakú, ahol és különböző egyjegyű prímszámok? (A) 12; (B) 90; (C) 91; (D) 2009; (E) 2100.
27. Huszonhét egységkockából egy -as kockát építettünk. Két egységkocka jó párt alkot, ha legfeljebb egy közös élük van. Hány jó pár található a kockában? (A) 256; (B) 270; (C) 297; (D) 333; (E) 351.
28. Tizenöt pozitív egész szám mediánja 2, átlaga 100. Mennyi a tizenöt szám móduszának lehetséges legnagyobb értéke, ha egyetlen módusz van? (A) 247; (B) 248; (C) 268; (D) 289; (E) 296.
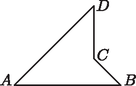
29. Az ábrán látható konkáv négyszög átlójának hossza 4 cm, a négyszög , és csúcsainál lévő belső szögek mindegyike . Hány négyzetcentiméter a négyszög területe? (A) 4; (B) 4,8; (C) 6,4; (D) 8; (E) 10.
30. Hány fok lehet az alábbiak közül az háromszög szögének nagysága, ha , ahol , és a háromszög három oldalának a hossza, a szög pedig a oldallal szemben fekvő szög? (A) ; (B) ; (C) ; (D) ; (E) .
| A feladatsort Csordásné Szécsi Jolán állította össze |
A középiskolás tanárverseny eredménye
1. Fridrik Richárd (Szegedi Tudományegyetem) ..... 136 pont
2. Tigyi István (Szeged, Radnóti Miklós Kís. Gimn.) ..... 135 pont
3. Fonyó Lajos (Keszthely, Vajda János Gimn.) ..... 135 pont
4. Kosztolányiné Nagy Erzsébet (Szeged, Radnóti Miklós Kís. Gimn.) ..... 129 pont
5. Kiss Géza (Budapesti Fazekas M. Ált. Isk. és Gimn.) ..... 127 pont
6. Magyar Zsolt (Budapest, Szent István Gimn.) ..... 124 pont
7. Vértes Judit (Budapest, Bálint Márton Ált.- és Középisk.) ..... 121 pont
8. Besnyőné Titter Beáta (Budapest, Árpád Gimn.) ..... 115 pont
9. Szaszkó-Bogárné Eckert Bernadett (Szeged, Radnóti Miklós Kís. Gimn.) ..... 113 pont
10. Nemecskó István (Budapest, Berzsenyi Dániel Gimn.) ..... 111 pont.
Az általános iskolás tanárverseny eredménye
1. B. Varga József (Temerin, Petar Kocsity Ált. Isk.) ..... 115 pont
2. Csordás Péter (Kecskemét, Katona József Gimn.) ..... 113 pont
3. Egyed László (Baja, III. Béla Gimn.) ..... 109 pont
4. Nagy Emese Hajnalka (Budapest, Kempelen Farkas Gimn.) ..... 106 pont
5. Nagy Tibor (Kecskemét, Kecskeméti Református Ált. Isk.) ..... 104 pont
6. Csordás Mihály (Kecskemét, Kodály Zoltán Ének-Zenei Ált. Isk.) ..... 101 pont.
Az általános iskolás tanárverseny feladatait nem közöljük. |
 PDF | MathML
PDF | MathML