Cím:	Megoldásvázlatok a 2014/6 sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Számadó László
Füzet:	2014/október, 399 - 409. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. Oldjuk meg a valós számok halmazán a következő egyenleteket: $a)$ $\text{cos}\left(3x-\frac{\pi }{6}\right)=-\frac{\sqrt[]{3}}{2}$; $b)$ $\text{log}{}_{2}x+\text{log}{}_{4}x=21$.  (11 pont)   Megoldás. $a)$ A nevezetes szögek szögfüggvényeit felhasználva az egyenlet jobb oldalára írjunk $\text{cos}\frac{5\pi }{6}$-ot: $\begin{array}{c}{\displaystyle \text{cos}\left(3x-\frac{\pi }{6}\right)=\text{cos}\frac{5\pi }{6}\mathrm{.}}\end{array}$ Tudjuk, hogy ha $\text{cos}\alpha =\text{cos}\beta$, akkor I. $\alpha -\beta =2k_1\pi$, ahol $k_1\in \text{Z}$; II. $\alpha +\beta =2k_2\pi$, ahol $k_2\in \text{Z}$. Most $\alpha =3x-\frac{\pi }{6}$, $\beta =\frac{5\pi }{6}$. Ezeket felhasználva kapjuk, hogy ${\displaystyle \begin{array}{ccccccccc}\hfill {\displaystyle 3x-\frac{\pi }{6}-\frac{5\pi }{6}}& {\displaystyle =2k_1\pi \mathrm{,}}\hfill & {\displaystyle 3x}\hfill & \hfill {\displaystyle =\pi +2k_1\pi \mathrm{,}}& {\displaystyle x_1}\hfill & {\displaystyle =\frac{\pi }{3}+k_1\cdot \frac{2\pi }{3}\mathrm{,}}\hfill & \hfill {\displaystyle \text{ahol }}& {\displaystyle k_1\in \text{Z}\mathrm{.}}\hfill & \text{(<mi>I</mi><mn>.</mn>)}\\ \hfill {\displaystyle 3x-\frac{\pi }{6}+\frac{5\pi }{6}}& {\displaystyle =2k_2\pi \mathrm{,}}\hfill & {\displaystyle 3x}\hfill & \hfill {\displaystyle =-\frac{2\pi }{3}+2k_2\pi \mathrm{,}}& {\displaystyle x_2}\hfill & {\displaystyle =-\frac{2\pi }{9}+k_2\cdot \frac{2\pi }{3}\mathrm{,}}\hfill & \hfill {\displaystyle \text{ahol }}& {\displaystyle k_2\in \text{Z}\mathrm{.}}\hfill & \text{(<mi>I</mi><mi>I</mi><mn>.</mn>)}\end{array}}$ Mivel ekvivalens átalakításokat végeztünk, ezért az egyenlet gyökei $x_1$ és $x_2$. $b)$ A két logaritmus csak akkor értelmezhető, ha $x>0$. A 4-es alapról térjünk át 2-es alapra: $\begin{array}{c}{\displaystyle \text{log}{}_{4}x=\frac{\text{log}{}_{2}x}{\text{log}{}_{2}4}=\frac{\text{log}{}_{2}x}{2}\mathrm{.}}\end{array}$ Ekkor ezt az egyenletet kapjuk: $\begin{array}{c}{\displaystyle \text{log}{}_{2}x+\frac{\text{log}{}_{2}x}{2}=21\mathrm{,}2\cdot \text{log}{}_{2}x+\text{log}{}_{2}x=\mathrm{42,}\text{log}{}_{2}x=14.}\end{array}$ A logaritmus definícióját használva: $x=2^{14}=16384$. Ez valóban megoldása az egyenletnek, hiszen benne van az értelmezési tartományban, az átalakításaink pedig ekvivalensek voltak.   2. $a)$ Gábor $18$. születésnapjára $18$ vendég volt hivatalos. A vendégek mindegyike pontosan négy vendéget ismert. Az est folyamán minden vendég tombolasorsoláson vett részt. Mennyi annak a valószínűsége, hogy a tombolasorsolás két nyertese ismeri egymást? $b)$ Hány csúcsa van annak a fagráfnak, amelybe $78$ élt kell berajzolnunk, hogy teljes gráfot kapjunk?  (12 pont)   Megoldás. $a)$ A 18 vendéget egy 18 pontú gráffal tudjuk szemléltetni. Két pontot akkor kötünk össze, ha a két pont olyan két vendéget szemléltet, akik ismerik egymást. A feladat szövege szerint ebben a gráfban $\frac{18\cdot 4}{2}=36$ él található. Ha mindenki mindenkit ismerne, akkor ennek a teljes gráfnak $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{18}{2}\right)=\frac{18\cdot 17}{1\cdot 2}=153}\end{array}$ éle lenne. A véletlenszerűen kisorsolt két nyertes ennek a teljes gráfnak valamelyik élét határozza meg. Ők csak akkor ismerik egymást, ha az előbb összeszámolt 36 él valamelyikét határozzák meg. A keresett valószínűséget a kedvező esetek számának és az összes esetek számának a hányadosa adja: $\begin{array}{c}{\displaystyle p=\frac{36}{153}=\frac{4}{17}\approx 0\mathrm{,}235.}\end{array}$ $b)$ Az $n$ pontú fagráfnak $n-1$ éle van, az $n$ pontú teljes gráfnak pedig 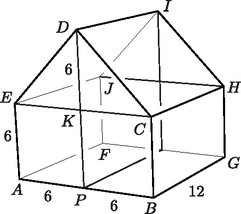$\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{n}{2}\right)=\frac{n\cdot \left(n-1\right)}{2}\mathrm{.}}\end{array}$ A feladat szövege szerint felírhatjuk a következő egyenletet: $\begin{array}{c}{\displaystyle \frac{n\cdot \left(n-1\right)}{2}=\left(n-1\right)+\mathrm{78,}{n}^2-n=2n+\mathrm{154,}{n}^2-3n-154=0.}\end{array}$ A kapott másodfokú egyenlet két gyöke: $n_1=14$, $n_2=-11$. A feladat szövegének csak a pozitív gyök tesz eleget. Vagyis a keresett fagráfnak 14 csúcsa van.   3. A vázlatrajz egy házikóra hasonlító ötszögalapú egyenes hasáb vázlatát mutatja. Ezt a szemléltetőeszközt egy 12 cm élű bükkfakockából fűrészelték ki. A házikó hossza, szélessége, magassága 12 cm, a tető két síkja merőleges egymásra és egybevágó.     $a)$ Mekkora a test felszíne? $b)$ Mennyivel lenne könnyebb ez a szemléltetőeszköz, ha lucfenyőből készítették volna? (A bükkfa sűrűsége $0\mathrm{,}68\frac{\text{<span style="font-weight: normal;font-style: normal;">g</span>}}{{\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^3}$, a lucfenyő sűrűsége $0\mathrm{,}43\frac{\text{<span style="font-weight: normal;font-style: normal;">g</span>}}{{\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^3}$.)  (14 pont)   Megoldás. A megadott vázlatrajzra írjuk rá az ismert és a kikövetkeztethető adatokat. A továbbiakban az ábrán látható jelölést használjuk. $a)$ A feladat szövege alapján a hasáb alapja olyan ötszög, amely az $EC$ átló és a $DP$ egyenes mentén két 6 cm oldalú négyzetre és két 6 cm befogójú egyenlő szárú derékszögű háromszögre vágható. Vagyis az ötszög területe: $\begin{array}{c}{\displaystyle T=2\cdot 6^2+2\cdot \frac{6^2}{2}=108\left({\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^2\right)\mathrm{.}}\end{array}$ A hasáb palástját a 12 cm oldalú $ABGF$ négyzet, a két 12 cm és 6 cm oldalú $BGHC$, illetve $AFJE$ téglalap, valamint a két egybevágó $CHDI$, $EJDI$ téglalap alkotja. Ezeknek a téglalapoknak az egyik oldaluk szintén 12 cm, a másik oldaluk pedig egyenlő a 6 cm befogójú egyenlő szárú derékszögű háromszög átfogójával, azaz $6\sqrt[]{2}$ cm hosszúságúak. Ezeket felhasználva a palást területe: $\begin{array}{c}{\displaystyle P=12\cdot \left(12+6+6\sqrt[]{2}+6\sqrt[]{2}+6\right)=288+144\sqrt[]{2}\approx 491\mathrm{,}6\left({\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^2\right)\mathrm{.}}\end{array}$ A hasáb felszíne: $\begin{array}{c}{\displaystyle A=2T+P=2\cdot 108+491\mathrm{,}6=707\mathrm{,}6\left({\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^2\right)\mathrm{.}}\end{array}$ $b)$ A test a $PQID$ és az $ECHJ$ síkok mentén szétdarabolható olyan 12 cm magasságú hasábokra, amelyekből 3 darab 6 cm alapélű 12 cm magasságú négyzetes oszlop illeszthető össze. Vagyis a térfogata a 12 cm élű kocka térfogatának a háromnegyede lesz: $\begin{array}{c}{\displaystyle V=\frac{3}{4}\cdot {12}^3=1296\left({\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^3\right)\mathrm{.}}\end{array}$ Vagyis a bükkfából készült kocka tömege $1296\cdot 0\mathrm{,}68=881\mathrm{,}28$ gramm. Ha lucfenyőből készült volna, akkor a tömege $1296\cdot 0\mathrm{,}43=557\mathrm{,}28$ gramm lenne. Vagyis ekkor 324 grammal lenne könnyebb. Megjegyzés. Természetesen az $a)$ részben kapott $T=108$ felhasználásával is adódik a hasáb térfogata: $V=108\cdot 12=1296\left({\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^3\right)$.   4. Két dobókockával $24$-szer dobtunk. A dobott számok összege a következő gyakorisági táblázatot adta:   ${\displaystyle \begin{array}{|cccccccccccc|}\hline {\displaystyle \text{Dobott érték}}\hfill & \hfill {\displaystyle \text{2}}& \hfill {\displaystyle \text{3}}& \hfill {\displaystyle \text{4}}& \hfill {\displaystyle \text{5}}& \hfill {\displaystyle \text{6}}& \hfill {\displaystyle \text{7}}& \hfill {\displaystyle \text{8}}& \hfill {\displaystyle \text{9}}& \hfill {\displaystyle \text{10}}& \hfill {\displaystyle \text{11}}& \hfill {\displaystyle \text{12}}\\ {\displaystyle \text{Gyakoriság}}\hfill & \hfill {\displaystyle \text{0}}& \hfill {\displaystyle \text{1}}& \hfill {\displaystyle \text{2}}& \hfill {\displaystyle \text{4}}& \hfill {\displaystyle \text{5}}& \hfill {\displaystyle \text{7}}& \hfill {\displaystyle \text{3}}& \hfill {\displaystyle \text{1}}& \hfill {\displaystyle \text{1}}& \hfill {\displaystyle \text{0}}& \hfill {\displaystyle \text{0}}\\ \hline\end{array}}$   $a)$ Mutassuk meg, hogy a huszonötödik dobás értéke nem lehet olyan, hogy a dobások értékének számtani közepe, mediánja, módusza valamilyen sorrendben egy nem állandó számtani sorozat három egymást követő tagja legyen. $b)$ Az elméletileg számított valószínűségekhez képest melyiket mondhatjuk szélsőségesebbnek, azt hogy $7$ darab $7$-est, vagy azt, hogy csak $3$ darab $8$-ast dobtunk?  (14 pont)   Megoldás. Legyen a huszonötödik dobás értéke $x$. Ekkor a huszonöt szám számtani közepe: $\begin{array}{c}{\displaystyle \frac{1\cdot 3+2\cdot 4+4\cdot 5+5\cdot 6+7\cdot 7+3\cdot 8+1\cdot 9+1\cdot 10+x}{25}=\frac{153+x}{25}\mathrm{.}}\end{array}$ A gyakorisági táblázat szerint hétszer volt 7-es dobás, a következő gyakoriság pedig az 5. Vagyis a huszonötödik dobástól függetlenül a számsokaság módusza a 7 lesz. Ha növekedő sorrendben nézzük a számsokaság tagjait, akkor a tizenkettedik helyen 6-os, a tizenharmadik helyen 7-es áll. Ezt látva a mediánra két eset adódik. Ha a huszonötödik dobás 6-nál nem nagyobb, akkor a medián 6 lesz. Ha a huszonötödik dobás 7-nél nem kisebb, akkor a medián 7 lesz. A feladat szövege szerint a módusz és a medián is nem lehet 7, mert a számtani sorozat tagjai nem állandók. Vagyis csak az lehetséges, hogy a medián 6, a módusz pedig 7. Ezekhez a számtani közép értéke háromféle lehetne: 5, $\frac{13}{2}$, 8. A $\frac{153+x}{25}=5$ egyenlet megoldása: $x=-28$. A $\frac{153+x}{25}=\frac{13}{2}$ egyenlet megoldása: $x=9\mathrm{,}5$. A $\frac{153+x}{25}=8$ egyenlet megoldása: $x=47$. Egyik esetben sem kaptunk megfelelő egész számot, ezzel a feladat állítását igazoltuk. $b)$ Két különböző kockával dobunk, az összes esetek száma 36. A dobott összeg 7 a következő esetekben lesz: $1+6$, $2+5$, $3+4$, $4+3$, $5+2$, $6+1$, azaz 6 a kedvező esetek száma. A dobott összeg 8 a következő esetekben lesz: $2+6$, $3+5$, $4+4$, $5+3$, $6+2$, azaz 5 a kedvező esetek száma. A hetes dobás valószínűsége $\frac{6}{36}$, a relatív gyakorisága pedig $\frac{7}{24}$. Az eltérés: $\begin{array}{c}{\displaystyle \left|\frac{6}{36}-\frac{7}{24}\right|=\left|\frac{12}{72}-\frac{21}{72}\right|=\frac{1}{8}\mathrm{.}}\end{array}$ A nyolcas dobás valószínűsége $\frac{5}{36}$, a relatív gyakorisága pedig $\frac{3}{24}$. Az eltérés: $\begin{array}{c}{\displaystyle \left|\frac{5}{36}-\frac{3}{24}\right|=\left|\frac{10}{72}-\frac{9}{72}\right|=\frac{1}{72}\mathrm{.}}\end{array}$ A hetes dobásnál nagyobb az eltérés a relatív gyakoriság és a valószínűség között, mint a nyolcas dobásnál, ezért a 24 dobás során az a szélsőségesebb, hogy hét darab hetest dobtunk.   II. rész     5. Adott a koordináta-rendszerben az $A\left(-1;0\right)$, $B\left(1;0\right)$ pontpár, továbbá a $C_n$ nemnegatív koordinátájú pontok, amelyekre $A{C}_n=B{C}_n=n$, ahol $n\in {\text{N}}^{+}$. Legyen $a_n=C_{n+1}{C}_n$. $a)$ Adjuk meg az $\left\{a_n\right\}$ sorozat első három tagját. $b)$ Igazoljuk, hogy $\left\{a_n\right\}$ szigorúan monoton csökkenő sorozat. $c)$ Mutassuk meg, hogy az $\left\{a_n\right\}$ sorozatnak az $1$ alsó korlátja.  (16 pont)   Megoldás. $a)$ A feladat szövege szerint: 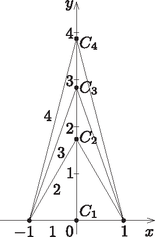$a_1=C_2{C}_1$, $a_2=C_3{C}_2$, $a_3=C_4{C}_3$.     Az $AB{C}_2$ szabályos háromszög magassága $C_2{C}_1$. Mivel a háromszög oldalhossza 2 egység, ezért $a_1=C_2{C}_1=\sqrt[]{3}$. Az $AB{C}_3$ egyenlő szárú háromszög alaphoz tartozó magasságának hosszát Pitagorasz-tétellel meghatározhatjuk: $C_3{C}_1=\sqrt[]{3^2-1^2}=\sqrt[]{8}$. Ekkor $\begin{array}{c}{\displaystyle a_2=C_3{C}_2=C_3{C}_1-C_2{C}_1=\sqrt[]{8}-\sqrt[]{3}\mathrm{.}}\end{array}$ Az $AB{C}_4$ egyenlő szárú háromszögben az előzőhöz hasonlóan járunk el. Kapjuk, hogy $C_4{C}_1=\sqrt[]{4^2-1^2}=\sqrt[]{15}$. Ekkor $\begin{array}{c}{\displaystyle a_3=C_4{C}_3=C_4{C}_1-C_3{C}_1=\sqrt[]{15}-\sqrt[]{8}\mathrm{.}}\end{array}$ Vagyis: $a_1=\sqrt[]{3}\approx 1\mathrm{,}732$, $a_2=\sqrt[]{8}-\sqrt[]{3}\approx 1\mathrm{,}096$, $a_3=\sqrt[]{15}-\sqrt[]{8}\approx 0\mathrm{,}045$. $b)$ Az $a)$ feladatban alkalmazott módszerrel megadjuk a sorozat $a_{n-1}$ és $a_n$ tagját. Az $AB{C}_{n-1}$, $AB{C}_n$, $AB{C}_{n+1}$ egyenlő szárú háromszögek alaphoz tartozó magasságának hosszát Pitagorasz-tétellel meghatározzuk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle C_{n-1}{C}_1}& {\displaystyle =\sqrt[]{{\left(n-1\right)}^2-1^2}=\sqrt[]{n^2-2n}\mathrm{,}}\hfill \\ \hfill {\displaystyle C_n{C}_1}& {\displaystyle =\sqrt[]{n^2-1^2}=\sqrt[]{n^2-1}\mathrm{,}}\hfill \\ \hfill {\displaystyle C_{n+1}{C}_1}& {\displaystyle =\sqrt[]{{\left(n+1\right)}^2-1^2}=\sqrt[]{n^2+2n}\mathrm{.}}\hfill \end{array}}$ Vagyis ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a_{n-1}}& {\displaystyle =C_n{C}_{n-1}=C_n{C}_1-C_{n-1}{C}_1=\sqrt[]{n^2-1}-\sqrt[]{n^2-2n}\mathrm{,}}\hfill \\ \hfill {\displaystyle a_n}& {\displaystyle =C_{n+1}{C}_n=C_{n+1}{C}_1-C_n{C}_1=\sqrt[]{n^2+2n}-\sqrt[]{n^2-1}\mathrm{.}}\hfill \end{array}}$ Meg kell mutatnunk, hogy az $\left\{a_n\right\}$ sorozat szigorúan monoton csökkenő, azaz meg kell mutatnunk, hogy minden 1-nél nagyobb pozitív egész $n$-re: $\begin{array}{c}{\displaystyle \sqrt[]{n^2-1}-\sqrt[]{n^2-2n}>\sqrt[]{n^2+2n}-\sqrt[]{n^2-1}\mathrm{.}}\end{array}$ A következő átalakítások ekvivalensek az 1-nél nagyobb pozitív egész $n$-ekre: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2\sqrt[]{n^2-1}}& {\displaystyle >\sqrt[]{n^2+2n}+\sqrt[]{n^2-2n}\mathrm{,}}\hfill \\ \hfill {\displaystyle 4\left(n^2-1\right)}& {\displaystyle >n^2+2n+2\sqrt[]{n^2+2n}\sqrt[]{n^2-2n}+n^2-2n\mathrm{,}}\hfill \\ \hfill {\displaystyle n^2-2}& {\displaystyle >\sqrt[]{n^2+2n}\sqrt[]{n^2-2n}\mathrm{,}}\hfill \\ \hfill {\displaystyle n^4-4n^2+4}& {\displaystyle >\left(n^2+2n\right)\left(n^2-2n\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle n^4-4n^2+4}& {\displaystyle >n^4-4n^2\mathrm{.}}\hfill \end{array}}$ Ez minden $n$-re teljesül, ezért az $\left\{a_n\right\}$ sorozat valóban szigorúan monoton csökkenő. $c)$ Meg kell mutatnunk, hogy az $\left\{a_n\right\}$ sorozat minden tagja nagyobb, vagy egyenlő, mint 1. Nézzük az $A{C}_n{C}_{n+1}$ háromszögeket ($n$ tetszőleges pozitív egész). A feladat szövege szerint: $A{C}_n=n$, $A{C}_{n+1}=n+1$, $C_{n+1}{C}_n=a_n$. Alkalmazzuk a háromszög-egyenlőtlenséget: $\begin{array}{c}{\displaystyle a_n+n>n+\mathrm{1,}{a}_n>1.}\end{array}$ Ezzel a feladat állítását beláttuk.   6. $a)$ A valós számok halmazán értelmezett $f\left(x\right)=x^3+a{x}^2+bx+c$ hozzárendeléssel adott függvényről tudjuk a következőket: I. $\underset{0}{\overset{1}{\int }}f\left(x\right)dx=\frac{53}{12}$. II. A $-2$ abszcisszájú pontjában húzott érintő egyenlete: $y=7x+29$. Adjuk meg $f\left(13\right)$ értékét. $b)$ Igazoljuk, hogy a valós számok halmazán értelmezett $f\left(x\right)=x^3-x^2-9x+9$ hozzárendeléssel adott függvénynek három zérushelye van.  (16 pont)   Megoldás. $a)$ Tudjuk, hogy $\underset{0}{\overset{1}{\int }}\left(x^3+a{x}^2+bx+c\right)dx=\frac{53}{12}$, vagyis: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left[\frac{x^4}{4}+a\frac{x^3}{3}+b\frac{x^2}{2}+cx\right]}_0^1}& {\displaystyle =\frac{53}{12}\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{1}{4}+\frac{a}{3}+\frac{b}{2}+c}& {\displaystyle =\frac{53}{12}\mathrm{,}}\hfill \\ \hfill {\displaystyle 3+4a+6b+12c}& {\displaystyle =\mathrm{53,}}\hfill \\ \hfill {\displaystyle 2a+3b+6c}& {\displaystyle =25.}\hfill \end{array}}$ Az érintő egyenletét ismerve meghatározhatjuk a függvény görbéjén a $-2$ abszcisszájú pont második koordinátáját: $y=7\cdot \left(-2\right)+29=15$. Azaz a $\left(-2;15\right)$ pont illeszkedik a függvény görbéjére. Ezeket a koordinátákat behelyettesítve a hozzárendelési szabályba: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle -8+4a-2b+c}& {\displaystyle =\mathrm{15,}}\hfill \\ \hfill {\displaystyle 4a-2b+c}& {\displaystyle =23.}\hfill \end{array}}$ Az érintő egyenletéből leolvasható, hogy a $\left(-2;15\right)$ pontban húzott érintő meredeksége 7. Az érintő meredekségét deriválással kaphatjuk: $\begin{array}{c}{\displaystyle \left(x^3+a{x}^2+bx+c\right)\text{'}={3x}^2+2ax+b\mathrm{.}}\end{array}$ Mivel -2-nél 7 a meredekség, ezért: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 3{\left(-2\right)}^2+2a\left(-2\right)+b}& {\displaystyle =\mathrm{7,}}\hfill \\ \hfill {\displaystyle -4a+b}& {\displaystyle =-5.}\hfill \end{array}}$ Az $a$, $b$ és $c$ együtthatókra a következő három egyenletből álló, három ismeretlenes egyenletrendszert kaptuk: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle 2a+3b+6c}& {\displaystyle =25}\hfill \\ \hfill {\displaystyle 4a-2b+c}& {\displaystyle =23}\hfill \\ \hfill {\displaystyle -4a+b}& {\displaystyle =-5.}\hfill \end{array}}\}}\end{array}$ A második egyenlet 6-szorosából kivonva az első egyenletet, a harmadik egyenletet pedig 15-tel szorozva: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle 22a-15b}& {\displaystyle =113}\hfill \\ \hfill {\displaystyle -60a+15b}& {\displaystyle =-75.}\hfill \end{array}}\}}\end{array}$ Összeadás után: $-38a=38$, amiből $a=-1$. Visszahelyettesítéssel: $b=-9$, $c=9$. Az együtthatók ismeretében: $\begin{array}{c}{\displaystyle f\left(x\right)=x^3-x^2-9x+9.}\end{array}$ A kérdéses függvényérték: $f\left(13\right)={13}^3-{13}^2-9\cdot 13+9=1920$. $b)$ Kiemelésekkel szorzattá alakítjuk a függvény hozzárendelési szabályában szereplő harmadfokú kifejezést: $\begin{array}{c}{\displaystyle f\left(x\right)=x^3-x^2-9x+9=x^2\left(x-1\right)-9\left(x-1\right)=\left(x-1\right)\left(x^2-9\right)\mathrm{.}}\end{array}$ Az $a^2-b^2=\left(a-b\right)\left(a+b\right)$ nevezetes azonosságot alkalmazva $\left(x^2-9\right)$-re: $\begin{array}{c}{\displaystyle f\left(x\right)=\left(x-1\right)\left(x-3\right)\left(x+3\right)\mathrm{.}}\end{array}$ Vagyis valóban három zérushelye van a függvénynek: $-3$, 1, 3.   7. $a)$ A $K\left(4;2\right)$ középpontú, $\sqrt[]{40}$ sugarú kör és az $x$ tengely két metszéspontja legyen $A$ és $B$. Az $ABC$ háromszögben $AC=BC$, továbbá az $ABC$ háromszög beírt körének középpontja $K$. Adjuk meg a $C$ pont koordinátáit. $b)$ Az $y=x^2-2x-3$ egyenletű parabola és az $x$ tengely két metszéspontja legyen $A$ és $B$. Az $AB$ szakasz felezőpontját $F$-fel, a parabola tengelypontját $T$-vel jelöljük, a parabolához $A$-ban és $B$-ben húzott érintők metszéspontját pedig $C$-vel. Mutassuk meg az egy egyenesre illeszkedő $F$, $T$, $C$ pontokra, hogy $T$ az $FC$ szakasz felezőpontja.  (16 pont)   Megoldás. $a)$ A megadott középponttal és sugárral felírható a kör egyenlete: 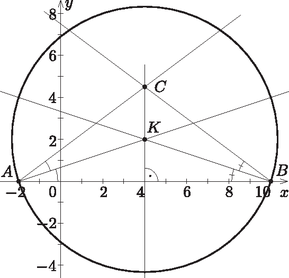$\begin{array}{c}{\displaystyle {\left(x-4\right)}^2+{\left(y-2\right)}^2=40.}\end{array}$     Mivel az $A$ és a $B$ pontok illeszkednek az $x$ tengelyre, ezért második koordinátájuk nulla. Ezek a pontok a körre is illeszkednek, ezért a kör egyenletéből $y=0$ helyettesítéssel megkapjuk a pontok első koordinátáit: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(x-4\right)}^2+{\left(0-2\right)}^2}& {\displaystyle =\mathrm{40,}}\hfill \\ \hfill {\displaystyle {\left(x-4\right)}^2}& {\displaystyle =\mathrm{36,}}\hfill \\ \hfill {\displaystyle |x-4|}& {\displaystyle =6.}\hfill \end{array}}$ Vagyis: $x_1=-2$, $x_2=10$. Ezek alapján a keresett metszéspontok: $A\left(-2;0\right)$, $B\left(10;0\right)$. Mivel $ABC$ egyenlő szárú háromszög és $AC$, $BC$ a két szára, ezért a $C$ pont az $AB$ szakasz felezőmerőlegesére illeszkedik. Ez az egyenes merőleges az $x$ tengelyre. Az $A$ és $B$ pontok ismeretében megadhatjuk az egyenletét: $x=\frac{-2+10}{2}=4$. Vagyis az erre az egyenesre illeszkedő $C$ pont első koordinátája is 4. Tudjuk, hogy az $ABC$ háromszög beírt körének középpontja $K$, ezért a háromszög $BAC$ szögének (az $\alpha$-nak) $AK$ a szögfelezője. Az $A$ és a $K$ ismeretében az $AK$ egyenes egyenlete: $\begin{array}{c}{\displaystyle \left(y-0\right)\left(4-\left(-2\right)\right)=\left(x-\left(-2\right)\right)\left(2-0\right)\mathrm{,}\text{azaz}y=\frac{1}{3}\left(x+2\right)\mathrm{.}}\end{array}$ Ennek az egyenesnek $\frac{1}{3}$ a meredeksége. Ez azt jelenti, hogy $\text{tg}\frac{\alpha }{2}=\frac{1}{3}$. Ha ennek ismeretében megadnánk a $\text{tg}\alpha$ értékét, akkor felírhatnánk az $AC$ egyenes egyenletét. Használjuk a függvénytáblázatban is megtalálható $\text{tg}2x=\frac{2\text{tg}x}{1-\text{tg}{}^{2}x}$ azonosságot. A $2x$ helyére írjunk $\alpha$-t: $\begin{array}{c}{\displaystyle \text{tg}\alpha =\frac{2\text{tg}\frac{\alpha }{2}}{1-\text{tg}{}^2\frac{\alpha }{2}}=\frac{2\cdot \frac{1}{3}}{1-{\left(\frac{1}{3}\right)}^2}=\frac{3}{4}\mathrm{.}}\end{array}$ Az $A$ pontra illeszkedő, $\frac{3}{4}$ meredekségű egyenes egyenlete: $y=\frac{3}{4}\left(x+2\right)$. Az erre illeszkedő $C$ pont első koordinátáját már ismerjük, ezért az $x=4$ behelyettesítésével a második koordinátáját is megkapjuk: $y=\frac{3}{4}\left(4+2\right)=\frac{9}{2}$. A keresett pont koordinátái: $C\left(4;\frac{9}{2}\right)$. $b)$ Mivel az $A$ és a $B$ pontok illeszkednek az $x$ tengelyre, ezért második koordinátájuk nulla. Ezek a pontok a parabolára is illeszkednek, ezért a parabola egyenletéből az $y=0$ helyettesítéssel kapott másodfokú egyenlet megoldásai adják a hiányzó koordinátákat. Az 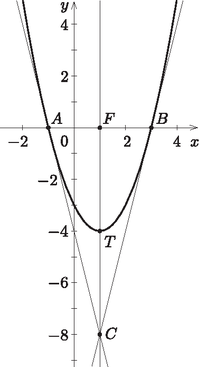$\begin{array}{c}{\displaystyle x^2-2x-3=0}\end{array}$ egyenlet megoldásai: $x_1=-1$, $x_2=3$.     Vagyis a parabola és az $x$ tengely két metszéspontja: $A\left(-1;0\right)$, $B\left(3;0\right)$, az $AB$ szakasz felezőpontja pedig: $F\left(1;0\right)$. A feladatban szereplő parabola függőleges tengelyű, és ez a tengely illeszkedik az $F$ pontra, vagyis $x=1$ az egyenlete. A tengely és a parabola metszéspontja adja a tengelypontot, aminek az első koordinátája 1, a másodikat a parabola egyenletéből behelyettesítéssel megkapjuk: $y=1^2-2\cdot 1-3=-4$. A parabola tengelypontja ezek alapján: $T\left(1;-4\right)$. A parabola $A$-ban és $B$-ben húzott érintői szimmetrikusak a parabola tengelyére, vagyis az $x=1$ egyenletű egyenesen metszik egymást. Ezért elegendő az egyik érintő egyenletét felírnunk, és azt megnézni, hogy hol metszi a parabola tengelyét. Írjuk fel a $B\left(3;0\right)$ pontban húzott érintő egyenletét. Az érintő iránytangensét (meredekségét) deriválással kapjuk: $\left(x^2-2x-3\right)\text{'}=2x-2$. Az $x=3$ abszcisszájú ponthoz tehát $2\cdot 3-2=4$ meredekségű érintő tartozik. A $B$ pont és a meredekség ismeretében az érintő egyenlete: $y=4x-12$. Ennek az érintőnek és a parabola $x=1$ egyenletű tengelyének a metszéspontja: $C\left(1;-8\right)$. Ezzel beláttuk az $F\left(1;0\right)$, $T\left(1;-4\right)$, $C\left(1;-8\right)$ pontokra, hogy $T$ valóban az $FC$ szakasz felezőpontja.   Megjegyzés. A $b)$ feladat állítását deriválás nélkül is megmutathatjuk. Az $F\left(1;0\right)$ és a $T\left(1;-4\right)$ ismeretében már megadható annak a $C$ pontnak a koordinátája, amelyre $T$ az $FC$ szakasz felezőpontja lesz: $C\left(1;-8\right)$. Ezek után meg kell mutatnunk, hogy $CA$ és $CB$ egyenesek a parabola érintői. Természetesen a szimmetria miatt ezt elegendő az egyikről belátnunk. A $C$ és a $B$ ismeretében a $CB$ egyenes egyenlete: $y=4x-12$. Határozzuk meg a parabola és a $CB$ egyenes közös pontjainak számát. Ehhez a következő egyenletrendszert kell megoldanunk: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle y}& {\displaystyle =x^2-2x-3}\hfill \\ \hfill {\displaystyle y}& {\displaystyle =4x-12}\hfill \end{array}}\}\mathrm{.}}\end{array}$ Az egyenletrendszer egyedüli megoldása: $x=3$, $y=0$. Mivel az $y=4x-12$ egyenletű egyenes nem merőleges az $x$ tengelyre, ezért érintője a parabolának. Ezzel beláttuk a feladat állítását.   8. Határozzuk meg azt a legkisebb pozitív $x$ értéket, amelyre $a)$ $\text{lg}x$ és $\text{lg}2x$ egy derékszögű háromszög befogói, $\text{lg}3x$ pedig az átfogója; $b)$ $\text{sin}x$ és $\text{sin}2x$ egy derékszögű háromszög befogói, $\text{sin}3x$ pedig az átfogója.  (16 pont)   Megoldás. $a)$ A $\text{lg}{}^{2}x+\text{lg}{}^{2}2x=\text{lg}{}^{2}3x$ egyenletet kell megoldanunk. Alakítsuk az egyenletet: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{lg}{}^{2}x+{\left(\text{lg}2+\text{lg}x\right)}^2}& {\displaystyle ={\left(\text{lg}3+\text{lg}x\right)}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{lg}{}^{2}x+\text{lg}{}^{2}2+2\text{lg}2\text{lg}x+\text{lg}{}^{2}x}& {\displaystyle =\text{lg}{}^{2}3+2\text{lg}3\text{lg}x+\text{lg}{}^{2}x\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{lg}{}^{2}x+2\left(\text{lg}2-\text{lg}3\right)\text{lg}x+\text{lg}{}^{2}2-\text{lg}{}^{2}3}& {\displaystyle =0.}\hfill \end{array}}$ Az egyenlet $\text{lg}x$-re másodfokú, a megoldóképlettel meghatározzuk a gyököket: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(\text{lg}x\right)}_{1;2}}& {\displaystyle =\frac{-2\left(\text{lg}2-\text{lg}3\right)\pm \sqrt[]{4{\left(\text{lg}2-\text{lg}3\right)}^2-4\left(\text{lg}{}^{2}2-\text{lg}{}^{2}3\right)}}{2}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =-\left(\text{lg}2-\text{lg}3\right)\pm \sqrt[]{{\left(\text{lg}2-\text{lg}3\right)}^2-\left(\text{lg}{}^{2}2-\text{lg}{}^{2}3\right)}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\text{lg}\frac{3}{2}\pm \sqrt[]{\text{lg}{}^{2}2-2\text{lg}2\text{lg}3+\text{lg}{}^{2}3-\text{lg}{}^{2}2+\text{lg}{}^{2}3}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\text{lg}\frac{3}{2}\pm \sqrt[]{-2\text{lg}2\text{lg}3+2\text{lg}{}^{2}3}=\text{lg}\frac{3}{2}\pm \sqrt[]{2\text{lg}3\left(\text{lg}3-\text{lg}2\right)}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\text{lg}\frac{3}{2}\pm \sqrt[]{2\text{lg}3\text{lg}\frac{3}{2}}\mathrm{.}}\hfill \end{array}}$ Számológéppel: ${\displaystyle \begin{array}{cccc}\hfill {\displaystyle {\left(\text{lg}x\right)}_1}& {\displaystyle \approx 0\mathrm{,}\mathrm{586,}}\hfill & {\displaystyle \text{ahonnan }{x}_1}\hfill & \hfill {\displaystyle \approx 3\mathrm{,}\mathrm{85,}}\\ \hfill {\displaystyle {\left(\text{lg}x\right)}_2}& {\displaystyle \approx -0\mathrm{,}\mathrm{234,}}\hfill & {\displaystyle \text{ahonnan }{x}_2}\hfill & \hfill {\displaystyle \approx 0\mathrm{,}58.}\end{array}}$ A feltételeknek megfelelő legkisebb pozitív szám kerekítve $3\mathrm{,}85$. $b)$ A $\text{sin}{}^{2}x+\text{sin}{}^{2}2x=\text{sin}{}^{2}3x$ egyenletet kell megoldanunk. Ezt az egyenletet $\text{sin}{}^{2}2x=\text{sin}{}^{2}3x-\text{sin}{}^{2}x=\left(\text{sin}3x-\text{sin}x\right)\left(\text{sin}3x+\text{sin}x\right)$ alakra tudjuk hozni. Tovább alakítva: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{sin}{}^{2}2x}& {\displaystyle =\left(2\text{cos}2x\text{sin}x\right)\left(2\text{sin}2x\text{cos}x\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{sin}{}^{2}2x}& {\displaystyle =2\text{sin}2x\text{cos}2x\left(2\text{sin}x\text{cos}x\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{sin}{}^{2}2x}& {\displaystyle =2\text{sin}{}^{2}2x\text{cos}2x\mathrm{,}}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle =\text{sin}{}^{2}2x\left(2\text{cos}2x-1\right)\mathrm{.}}\hfill \end{array}}$ Az egyenlet megoldásai: $x_1=k_1\cdot \frac{\pi }{2}\mathrm{,}$ ahol $k_1\in \text{Z}$; $x_2=\frac{\pi }{6}+k_2\pi$, ahol $k_2\in \text{Z}$; $x_3=-\frac{\pi }{6}+k_3\pi$, ahol $k_3\in \text{Z}$. A feltételeknek megfelelő legkisebb pozitív szám a $\frac{\pi }{6}$.   9. A magyar kártyában négy szín található (zöld, makk, tök, piros) és minden színhez nyolc figura tartozik (VII, VIII, IX, X, alsó, felső, király, ász). Gyuri, Csaba és István ultiznak. Ezt a kártyajátékot magyar kártyával játsszák. Az osztás során mindenki tíz lapot kap, és két lap marad talonban. $a)$ Számítsuk ki annak a valószínűségét, hogy a talonba kerülő két lapon különböző figura lesz. $b)$ Mennyi annak a valószínűsége, hogy Gyuri megkapja mind a négy ászt? $c)$ Számítsuk ki annak a valószínűségét, hogy Csabánál nem lesz VII-es lap. $d)$ Ha tudjuk, hogy István kapott legalább egy VII-es lapot az osztáskor, akkor számítsuk ki annak a valószínűségét, hogy mind a négy VII-es hozzá kerül.  (16 pont)   Megoldás. $a)$ Összesen $\left(\genfrac{}{}{0ex}{}{32}{2}\right)=\frac{32\cdot 31}{1\cdot 2}=496$-féleképpen lehet 2 lapot kiválasztani a 32 lapos magyar kártyából. A két különböző figura $\left(\genfrac{}{}{0ex}{}{8}{2}\right)=\frac{8\cdot 7}{1\cdot 2}=28$-féleképpen fordulhat elő, és mindkettőnek 4 színe lehet. Ez $28\cdot 4\cdot 4=448$ eset. A keresett valószínűség: $\frac{448}{496}\approx 0\mathrm{,}903$. $b)$ Gyuri összesen $\left(\genfrac{}{}{0ex}{}{32}{10}\right)$-féleképpen kaphatja meg a lapjait. Mivel a kedvező esetben mind a négy ász nála van, ezért a maradék 28 lapból fog kapni még 6 lapot, ami $\left(\genfrac{}{}{0ex}{}{28}{6}\right)$-féleképpen történhet. Vagyis a keresett valószínűség: $\begin{array}{c}{\displaystyle \frac{\left(\genfrac{}{}{0ex}{}{28}{6}\right)}{\left(\genfrac{}{}{0ex}{}{32}{10}\right)}\approx 0\mathrm{,}006.}\end{array}$ $c)$ Csaba összesen $\left(\genfrac{}{}{0ex}{}{32}{10}\right)$-féleképpen kaphatja meg a lapjait. Mivel a most vizsgált (kedvező) esetben nincs nála VII-es, ezért a többi 28 lapból fogja megkapni a tíz lapját, ami $\left(\genfrac{}{}{0ex}{}{28}{10}\right)$-féleképpen történhet. Vagyis a keresett valószínűség: $\begin{array}{c}{\displaystyle \frac{\left(\genfrac{}{}{0ex}{}{28}{10}\right)}{\left(\genfrac{}{}{0ex}{}{32}{10}\right)}\approx 0\mathrm{,}203.}\end{array}$ $d)$ A feltételes valószínűség definíciója szerint: $P\left(B\mid A\right)=\frac{P\left(BA\right)}{P\left(A\right)}$. Jelen esetben $B$ azt az eseményt jelöli, hogy mind a négy VII-es lap Istvánhoz került, $A$ pedig azt, hogy van Istvánnál VII-es. Tudjuk, hogy $P\left(BA\right)=P\left(B\right)$, hiszen ha minden VII-es Istvánnál van, akkor van nála VII-es. A négy VII-es $\left(\genfrac{}{}{0ex}{}{28}{6}\right)$-féleképpen kerülhet Istvánhoz, ezért $\begin{array}{c}{\displaystyle P\left(B\right)=\frac{\left(\genfrac{}{}{0ex}{}{28}{6}\right)}{\left(\genfrac{}{}{0ex}{}{32}{10}\right)}\mathrm{.}}\end{array}$ Mivel $\frac{\left(\genfrac{}{}{0ex}{}{28}{10}\right)}{\left(\genfrac{}{}{0ex}{}{32}{10}\right)}$ annak a valószínűsége, hogy egy megadott játékosnál nincs VII-es lap, ezért $\begin{array}{c}{\displaystyle P\left(A\right)=1-\frac{\left(\genfrac{}{}{0ex}{}{28}{10}\right)}{\left(\genfrac{}{}{0ex}{}{32}{10}\right)}\mathrm{.}}\end{array}$ Ezek alapján a keresett valószínűség: $\begin{array}{c}{\displaystyle P\left(B\mid A\right)=\frac{\frac{\left(\genfrac{}{}{0ex}{}{28}{6}\right)}{\left(\genfrac{}{}{0ex}{}{32}{10}\right)}}{1-\frac{\left(\genfrac{}{}{0ex}{}{28}{10}\right)}{\left(\genfrac{}{}{0ex}{}{32}{10}\right)}}\approx 0\mathrm{,}007.}\end{array}$