Cím:	Emelt szintű gyakorló feladatsor
Szerző(k):	Czinki József
Füzet:	2014/október, 396 - 398. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész   1. $a)$ Ábrázoljuk derékszögű koordinátarendszerben az $\begin{array}{c}{\displaystyle f:x\in \left[-3;13\right[\mathrm{,}x\mapsto -\sqrt[]{x+3}+5}\end{array}$ függvényt. $b)$ Ábrázoljuk az előzővel azonos koordinátarendszerben a $\begin{array}{c}{\displaystyle g:x\in \left[-3;13\right[\mathrm{,}x\mapsto \left|-\left|x-3\right|+3\right|+2}\end{array}$ függvényt. $c)$ Vizsgáljuk meg a függvényeket szélsőértékek szempontjából. $d)$ A függvényábrák segítségével oldjuk meg a következő egyenlőtlenséget: $f\left(x\right)\ge g\left(x\right)$.  (11 pont)   2. Tekintsük a következő öt állítást: $A$: Nem létezik olyan pozitív egészekből álló, öttagú számtani sorozat, amelyre igaz, hogy bármely két elemének a legnagyobb közös osztója 1. $B$: Ha egy síkbeli négyszög húrnégyszög, akkor létezik a síkjában egy olyan pont, amelytől a négyszög minden csúcsa azonos távolságra van. $C$: Egy $n$ elemű halmaz összes részhalmazainak száma $n^2$. $D$: Ha egy $e$ egyenest 2014 db különböző sugarú kör ugyanabban az $E$ pontban érint, akkor e körök középpontjai egy egyenesre illeszkednek. $E$: Ha egy függvény periodikus, akkor képe szimmetrikus az $y$ tengelyre. $a)$ Állapítsuk meg, hogy melyik állítás igaz, és melyik állítás hamis. Indokoljuk válaszainkat. $b)$ Írjuk fel a $B$ és az $E$ állítások megfordítását, és állapítsuk meg az igazságértéküket. $c)$ Fogalmazzuk meg egy mondatban a $B$ állítást és a megfordítását. Igaz-e a kapott állítás? $d)$ Melyik a következő mondatok közül az $E$ állítás tagadása? I. Ha egy függvény nem periodikus, akkor képe szimmetrikus az $y$ tengelyre. II. Van olyan periodikus függvény, melynek képe nem szimmetrikus az $y$ tengelyre.  (12 pont)   3. Egy magashegységben meteorológiai kutatóállomás működik. A tereptárgyak pontos helyét térbeli koordinátarendszerbeli koordinátahármasok segítségével tartják nyilván, melynek egységét minden tengelyen 1 méternek választották, és origójában van a kutatóállomás. A koordinátarendszer $x$ tengelye délről észak felé mutat, $y$ tengelye keletről nyugat felé irányul, $z$ tengelye pedig függőleges, és felfelé irányul. A pontok koordinátáit $x$, $y$, $z$ sorrendben adják meg. A környéken három meghatározó hegycsúcs van, melyek koordinátái: $A\left(8200;21;1214\right)$; $B\left(-28;7600;1021\right)$; $C\left(-1200;-4550;900\right)$. $a)$ Melyik hegy van a kutatóállomástól megközelítőleg északi irányban? Milyen emelkedési szög alatt látja ennek a csúcsát a kutatóállomáson tartózkodó megfigyelő? $b)$ Mekkora az$A$, $B$ és a $C$ hegycsúcsok tengerszint feletti magassága, ha a $K\left(5120;-4170;-4752\right)$ pont éppen a tengerszinten található? $c)$ A kutatóállomásról havonta helikopter indul. A személyzet feladata az $A$, $B$ és a $C$ csúcsokon kihelyezett műszerekben az akkumulátorcsere. Mekkora utat tesz meg egy ilyen alkalommal a helikopter, ha a csúcsokat $A$ csúcs, $B$ csúcs, $C$ csúcs sorrendben járja be, majd visszatér a kutatóállomásra?  (14 pont)   4. $a)$ Egy számtani sorozat második eleme $\frac{5\sqrt[]{5}-2}{3}$, differenciája pedig $\sqrt[]{5}+1$. Mekkora az ötödik tag? Mennyi az első kilenc tag összege? $b)$ Ha egy számtani sorozat első tagjából levonunk kettőt, második tagjából levonunk egyet, és a harmadik tagjához hozzáadunk ötöt, akkor egy mértani sorozat első három elemét kapjuk. Melyik ez a számtani sorozat, ha tudjuk, hogy a kapott mértani sorozat első két elemének összege egyenlő az eredeti számtani sorozat harmadik tagjával? $c)$ Számítsuk ki a következő határértéket: $\begin{array}{c}{\displaystyle \underset{n\to \infty }{\overset{}{\text{lim}}}\frac{1}{\sqrt[]{2n+1}-\sqrt[]{n}}\mathrm{.}}\end{array}$  (14 pont)   II. rész     5. Az ábrán látható téglalap alakú csempéről tudjuk, hogy $DTA\sphericalangle =CSB\sphericalangle ={90}^{\circ }$, valamint $AT=6$ cm, $TS=14$ cm.     $a)$ Mekkora egy ilyen csempe területe? $b)$ Hány db ilyen csempét kell rendelnünk egy 25 m alapkörsugarú, 2,5 m mély, henger alakú medence kicsempézéséhez, ha a vágások és a törések miatt 15%-os ráhagyás szükséges? (A csempéket csomagokban árusítják, de számításaink során ezzel ne foglalkozzunk.) $c)$ Hány fordulóval képes ezt egy 4 tonna teherbírású teherautó elhozni, ha egy csempe 5 mm vastag, és anyagának sűrűsége $2520\frac{\text{<span style="font-weight: normal;font-style: normal;">kg</span>}}{{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}^3}$? $d)$ Rendelkezésünkre áll egy olyan szivattyú, amely a 10 cm átmérőjű csövében a vizet $1\frac{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}{\text{<span style="font-weight: normal;font-style: normal;">s</span>}}$ sebességgel képes áramoltatni. Mennyi idő alatt tudja majd ez a szivattyú a színültig teletöltött medencét kiüríteni?  (16 pont)   6. $a)$ Egy osztályba 16 fiú és 14 leány jár. Egy alkalommal 11 egyforma könyvet sorsolnak ki köztük úgy, hogy egy tanuló csak egy könyvet kaphat. Mennyi a valószínűsége, hogy fiú is és lány is lesz a nyertesek között? $b)$ Egy középiskolai menzán az ebédhez süteményt lehet választani. Kétféle sütemény van, édes és sós. A tapasztalatok szerint annak valószínűsége, hogy egy diák édes süteményt választ 0,75. Mennyi annak a valószínűsége, hogy négy egymás után következő diákra nem lesz igaz, hogy azonos típusú süteményt választanak, ha mindegyikük pontosan egy süteményt visz magával? $c)$ Egy harminc fős alsó tagozatos osztályban van egy ikerpár. A tanító néni egy játékhoz véletlenszerűen két 15 fős csapatba fogja őket sorsolni. Mennyi a valószínűsége annak, hogy az ikerpár két tagja nem azonos csapatba kerül?  (16 pont)   7. $a)$ Igazoljuk, hogy a $2^{2n}-1$ minden pozitív egész $n$ számra osztható hárommal. $b)$ Igazoljuk, hogy a $\frac{n-n^3}{6}$ kifejezés bármely $n$ egész szám behelyettesítése esetén egész számot ad eredményül. $c)$ Hány pozitív osztója van a ${{2014}^{11}\cdot 11}^{2014}$ számnak? $d)$ Négyzetszám-e a 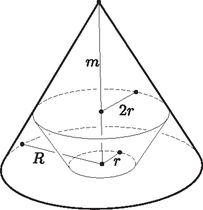$3^{2014}-1$?  (16 pont)   8. A képen látható $R=30$ cm alapkörsugarú, és $m=50$ cm magasságú egyenes kúpba egyenes csonkakúpokat írunk a következő feltételekkel:     ‐ A csonkakúp kisebb alapkörének sugara a nagyobb alapköre sugarának felével egyenlő. ‐ A csonkakúp nagyobb alapkörének körvonala a kúp palástjára illeszkedik. ‐ A csonkakúp kisebb alapköre a kúp alapsíkjára illeszkedik. $a)$ Mennyi az ilyen csonkakúpok közül a maximális térfogatú magassága? $b)$ Mekkora a csonkakúp felszíne és térfogata, ha $r=\frac{R}{3}$?  (16 pont)   9. $a)$ Oldjuk meg a következő egyenletet: $\begin{array}{c}{\displaystyle \frac{\text{sin}{}^{4}x+2\text{cos}x}{2\text{cos}{}^{4}x+2}={\sqrt[]{2}}^{\left(-\text{sin}{}^{2}x-\text{cos}{}^{2}x-1\right)}\mathrm{.}}\end{array}$ $b)$ Igazoljuk a következő egyenlőtlenséget: $\begin{array}{c}{\displaystyle \text{lg}\left(\frac{a^2}{3bc}+\frac{b^2}{3ac}+\frac{c^2}{3ab}\right)\ge \mathrm{0,}}\end{array}$ ahol $a$, $b$, $c$ tetszőleges pozitív valós számok.  (16 pont)