Kezdőlap


Cím:	Az 55. Nemzetközi Matematikai Diákolimpia feladatainak megoldásai
Füzet:	2014/október, 386 - 395. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A hagyományoknak megfelelően ebben az évben is közöljük a nyári matematikai diákolimpia feladatainak a megoldásait; lényegében úgy, ahogyan a legilletékesebbek, a magyar csapat tagjai leírták. Közreműködésüket köszönjük és ezúton is gratulálunk eredményeikhez.

A szerkesztőség

1. Legyen

a_{0} < a_{1} < a_{2} < ...

pozitív egészeknek egy végtelen sorozata. Bizonyítsuk be, hogy létezik egy egyértelműen meghatározott

n \geq 1

egész szám, amire

\begin{matrix} a_{n} < \frac{a_{0} + a_{1} + ... + a_{n}}{n} \leq a_{n + 1} . \end{matrix}

Homonnay Bálint megoldása. Tegyük fel, hogy egy

n

-re

\begin{matrix} \frac{a_{0} + a_{1} + ... + a_{n}}{n} \leq a_{n + 1} . \end{matrix}

Szorozva

n

-nel, hozzáadva

a_{n + 1}

-et és osztva

n + 1

-gyel azt kapjuk, hogy

\begin{matrix} \frac{a_{0} + a_{1} + ... + a_{n + 1}}{n + 1} \leq a_{n + 1}, \end{matrix}

tehát ha

n

-re igaz az állítás, akkor

n + 1

-re nem lehet az. Mivel a sorozat szigorúan monoton nő, ezért semmilyen

n

-nél nagyobb számra nem lehet igaz, tehát legfeljebb egy számra lehet igaz az állítás.
Mivel

a_{1} < \frac{a_{0} + a_{1}}{1}

, csak akkor nem lehet megoldás, ha minden

n

-re

\begin{matrix} \frac{a_{0} + a_{1} + ... + a_{n}}{n} > a_{n + 1} . \end{matrix}

Indukcióval belátjuk, hogy ha nincs megoldás, akkor minden

i

-re

\begin{matrix} a_{i + 1} < \frac{a_{0} + a_{1} + ... + a_{i}}{i} és a_{i} < a_{0} + a_{1} . \end{matrix}

Szorozva, majd használva az indukciós feltevést és a sorozat monotonitását:

\begin{matrix} i \cdot a_{i + 1} < a_{0} + a_{1} + ... + a_{i} < a_{0} + a_{1} + (i - 1) (a_{0} + a_{1}) = i (a_{0} + a_{1}), a_{i + 1} < a_{0} + a_{1}, \end{matrix}

illetve

i

-vel szorozva és

a_{i + 1}

-et hozzáadva

\begin{matrix} (i + 1) a_{i + 1} < a_{0} + a_{1} + ... + a_{i + 1}, azaz a_{i + 1} < \frac{a_{0} + a_{1} + ... + a_{i + 1}}{i + 1}; \end{matrix}

ha nincs megoldás, ekkor ebből valóban

a_{i + 2} < \frac{a_{0} + a_{1} + ... + a_{i + 1}}{i + 1}

következik. Mivel a sorozat szigorúan monoton növekszik,

i = a_{0} + a_{1} + 1

-re ez az állítás nem lehet igaz, tehát mindig van megoldás, és feljebb már igazoltuk, hogy ez egyértelmű.

2. Legyen

n \geq 2

egész szám. Tekintsünk egy

n^{2}

egységnégyzetből álló

n \times n

-es sakktáblát.

n

bástyának az elhelyezését ezen a sakktáblán békésnek nevezzük, ha minden sorban és minden oszlopban pontosan egy bástya áll. Határozzuk meg a legnagyobb olyan

k

pozitív egész számot, amire igaz az, hogy

n

bástya minden békés elhelyezéséhez található egy olyan

k \times k

-as négyzet, amelynek a

k^{2}

egységnégyzete egyikén sem áll bástya.

Maga Balázs megoldása. Be fogjuk bizonyítani, hogy amennyiben

i^{2} < n \leq {(i + 1)}^{2}

, ahol

i

pozitív egész, akkor

k = i

.
Ennek igazolásához két dolgot kell tennünk. Egyrészt bizonyítanunk kell, hogy minden lehetséges békés elrendezés esetén marad szabadon

i \times i

-s négyzet. Másrészt meg kell mutatnunk, hogy létezik a bástyáknak olyan békés elrendezése, ami esetén nem marad szabadon ennél nagyobb négyzet. Ezen lépéseket ebben a sorrendben tesszük meg.
I. Számozzuk meg az oszlopokat 1-től

n

-ig balról jobbra, a sorokat szintén lentről felfelé. Ekkor lesz olyan bástya, ami az 1. oszlopban van. Legyen ennek sorszáma

s_{1}

, ekkor ezen bástya koordinátái

(1, s_{1})

. Tekintsünk most úgy

i

darab szomszédos sort, hogy az

s_{1}

sor köztük van. Mivel

n > i^{2} \geq i

, ez lehetséges. Ezen

i

sorban még további

i - 1

bástya található

(1, s_{1})

-n kívül, mivel békés elrendezésben minden sorban pontosan egy bástya van. Indirekte tegyük fel, hogy ebben az

i

darab sorban nem marad szabadon

i \times i

-s négyzet. Ez azt jelenti, hogy bármely szomszédos

i

oszlopba kerül bástya ezen az

i

darab soron. Azaz ha tekintjük ezen bástyák oszlopszámát növekvő sorrendben (ezeket jelölje

1 = o_{1} < o_{2} < ... < o_{i}

), akkor tetszőleges

j \in 1,2, ..., i - 1

esetén

o_{j + 1} - o_{j} \leq i

. Ebből adódik, hogy

o_{i} \leq o_{1} + i \cdot (i - 1) = i^{2} - i + 1

. Mivel viszont

n > i^{2}

n \geq i^{2} + 1

, ezen

o_{i}

sorszámú oszlop után még legalább

i

darab oszlopban nincs bástya ezen az

i

darab soron. Ez viszont éppen azt jelenti, hogy szabadon marad egy

i \times i

-s négyzet. Ez ellentmondás, tehát valóban mindig marad szabadon

i \times i

-s négyzet.
II. Itt elegendő egy konstrukciót létrehoznunk, aminél nem marad szabadon

(i + 1) \times (i + 1)

-s négyzet. Helyezzük el bástyáinkat a következő módon: az 1. sorban levő bástya legyen az

(1,1)

mezőn. A második sorban levő legyen az

(i + 2,1 + 1)

mezőn. És így tovább, amint egy sorral feljebb lépünk, mindig

i + 1

oszloppal lépjünk jobbra, amíg ez lehetséges, azaz amíg az így kapott oszlopszám nem lépi túl az

n

-t. Ha viszont túllépi, válasszuk a legkisebb üres sor- és oszlopszámokkal rendelkező mezőt, azaz a

(2, s_{2})

-t. Innen indulva megint a fenti algoritmust követjük: 1 sorral feljebb,

i + 1

oszloppal jobbra, amíg ez lehetséges. Ha nem, a

(3, s_{3})

mezőt választjuk. Ezt az algoritmust folytatva pakoljuk fel a bástyákat, míg a sorszám el nem éri az

n

-t. Azt állítom, hogy az így kapott elrendezésben nem marad szabadon

(i + 1) \times (i + 1)

-s négyzet, azaz ez az elrendezés megfelel számunkra.
Először azt kell meggondolnunk, hogy egyáltalán békés elrendezéshez jutottunk-e, azaz igaz-e, hogy minden sorban és oszlopban pontosan 1 bástya van. Mivel

n

bástyát helyeztünk el, ez ekvivalens azzal, hogy egyik sorban vagy oszlopban sincs 1-nél több bástya. A sorokra ez nyilvánvaló, mivel a bástyák elhelyezése során egyesével lépdeltünk fel rajtuk. Egy oszlopban pedig azért nem lehet két bábu, mert először az

i + 1

-gyel 1 maradékot adó oszlopokon mentünk végig 1-től indulva

n

-ig, aztán a 2 maradékot adókon stb. Így a bástyák elhelyezése során maradékosztályonként soroltuk fel a számokat 1-től

n

-ig. Ekkor világos, hogy ugyanabba a maradékosztályba nem kezdhettünk bele kétszer, hiszen akkor már

n

-nél több bástyát kellett volna elhelyeznünk. Tehát valóban békés az elrendezésünk.
Tehát már csak azzal kell foglalkoznunk, hogy nem maradhatott

(i + 1) \times (i + 1)

-s négyzet szabadon. Ez ekvivalens azzal, hogy tetszőleges módon választva

i + 1

szomszédos sort, nincs úgy

i + 1

szomszédos oszlop, hogy mindegyik üres lenne ezen

i + 1

soron belül. Ezt fogjuk tehát bizonyítani.
Először nézzük azt az esetet, amikor van olyan

i + 1

-es maradékosztály, amit teljes egészében tartalmaz a kiválasztott

i + 1

darab sorunk, azaz a megjelenő oszlopszámok között ott van az összes 1 és

n

közötti szám, ami

i + 1

-gyel osztva egy adott

m

maradékot ad. Ekkor nyilván nincs olyan

i + 1

szomszédos oszlop, ami üres lenne ezen az

i + 1

soron, mivel tetszőleges

i + 1

szomszédos oszlop között van olyan, melynek sorszáma

m

maradékot ad

i + 1

-gyel osztva. Ezzel az esettel tehát készen vagyunk.
Tehát már csak azzal az esettel kell foglalkoznunk, amikor nincs olyan maradékosztály, ami teljes egészében fel lenne sorolva ebben az

i + 1

sorban. Ekkor tehát legalább 2 maradékosztály elemei jelennek meg, mint oszlopszámok. Másrészt mivel csak akkor váltunk maradékosztályt, ha az aktuálisat már teljes egészében felsoroltuk, nem lehetséges, hogy legalább 3 maradékosztály elemei jelenjenek meg, mint oszlopszámok, hiszen ekkor a nem szélsők összes 1 és

n

közötti reprezentánsa megjelenik az oszlopszámok között, márpedig azt ebben az esetben kizártuk.
Tehát valójában most már csak azzal foglalkozunk, amikor az

i + 1

szomszédos sorból álló blokkunk pontosan 2 maradékosztályból tartalmaz oszlopszámot. Legyenek ezek

m

és

m + 1

. Ekkor

m \neq 0

, mivel a maradékosztályokat 1-től indulva soroljuk fel, így ez a maradékosztály az utolsó.

m + 1

viszont lehet 0, ekkor rendhagyó módon

i + 1

-es maradéknak tekintjük mod

i + 1

az egyszerűség kedvéért. Ekkor az oszlopszámok a konstrukció megalkotási algoritmusa alapján lentről felfelé haladva:

a (i + 1) + m

(a + 1) (i + 1) + m

...

(a + a_{1}) (i + 1) + m

m + 1

(i + 1) + m + 1

...

b \cdot (i + 1) + m + 1

. Ekkor

b \geq a - 1

. Indirekte tegyük fel, hogy nincs így. Az imént

i + 1

sort vettünk fel, így a fent megjelenő

i + 1

együtthatók (

a

a + 1

...

a + a_{1}

, 0, 1,

...

b

) száma

i + 1

b < a - 1

esetén ezek mind eltérőek, továbbá

b + 1

is eltér mindtől. Így a

0 \cdot (i + 1)

1 \cdot (i + 1)

...

b \cdot (i + 1)

(b + 1) \cdot (i + 1)

a \cdot (i + 1)

(a + 1) \cdot (i + 1)

...

(a + a_{1}) \cdot (i + 1)

számok mind eltérőek, valamint mindegyik legalább 0 és kisebb, mint

n

, mivel a legnagyobb közülük

(a + a_{1}) \cdot (i + 1)

, s még

(a + a_{1}) \cdot (i + 1) + m \leq n

is igaz.
Tehát a nemnegatív,

n

-nél kisebb

i + 1

többszörösök száma legalább

i + 2

. Másrészt

n \leq {(i + 1)}^{2}

miatt a legnagyobb ilyen többszörös az

i \cdot (i + 1)

, a legkisebb pedig a

0 \cdot (i + 1)

, azaz az ilyen többszörösök száma valójában

i + 1

. Ez ellentmondás, tehát valóban

b \geq a - 1

. Ugyanakkor

b < a + a_{1}

. Ellenkező esetben ugyanis

n \geq b \cdot (i + 1) + m + 1 > (a + a_{1}) \cdot (i + 1) + m

. Ez utóbbi itt a legnagyobb

n

-nél nemnagyobb,

i + 1

-gyel osztva

m

maradékot adó szám. Így nyilván

b \cdot (i + 1) + m + 1

a legnagyobb

n

-nél nemnagyobb

i + 1

-gyel osztva

m + 1

maradékot adó szám. Ez viszont azt jelenti, hogy az

m + 1

-es maradékosztály összes

n

-nél nemnagyobb pozitív reprezentánsa megjelenik ebben az

i + 1

sorban, mint oszlopszám, ami ellentmond az esetünk kiinduló feltételével. Tehát

a - 1 \leq b < a + a_{1}

, azaz

a \leq b + 1 \leq a + a_{1}

. Tehát

(b + 1) \cdot (i + 1) + m

az itt megjelenő oszlopszámok között van. Ebből viszont már rövid úton következik, hogy nem maradhat üresen

i + 1

szomszédos oszlop ebben az

i + 1

sorban.
Először is a legkisebb oszlopszám

m + 1 \leq i + 1

, így az első

i + 1

oszlop biztosan nem üres. Utána

b \cdot (i + 1) + m + 1

-ig végig legfeljebb

i + 1

a különbség a szomszédos sorszámok között, nincs gond, továbbra sem maradhat üresen

i + 1

szomszédos oszlop. Ezt követően nem maradhat üresen

i + 1

oszlop, hiszen

(b + 1) \cdot (i + 1) + m - b \cdot (i + 1) + (m + 1) = i - 1

két oszlopszám különbsége. Innen viszont

(a + a_{1}) \cdot (i + 1) + m

-ig ismét végig

i + 1

a különbség az oszlopszámok között, mint az imént, azaz most sem maradhat üresen

i + 1

szomszédos oszlop. Ezen iménti oszlop pedig nem lehet

i + 1

-nél távolabb a tábla szélétől, mivel ez a legnagyobb

n

-nél nemnagyobb reprezentánsa egy

i + 1

-es maradékosztálynak. Azaz akárhogy választunk ki

i + 1

szomszédos sort, nem lesz bennük

i + 1

szomszédos üres oszlop. Tehát a konstrukciónk valóban megfelel az elvárásainknak. Ezzel készen vagyunk, valóban minden

n \geq 2

esetén, ha

i^{2} < n \leq {(i + 1)}^{2}

, akkor

k = i

3. Az

A B C D

konvex négyszögben

A B C ∢ = C D A ∢ = 90^{\circ}

. A

H

pont az

A

-ból

B D

-re bocsátott merőleges talppontja. Az

S

, illetve

T

pont úgy helyezkedik el az

A B

, illetve

A D

oldalszakaszon, hogy

H

S C T

háromszög belsejében van, és

\begin{matrix} C H S ∢ - C S B ∢ = 90^{\circ}, T H C ∢ - D T C ∢ = 90^{\circ} . \end{matrix}

Bizonyítsuk be, hogy a

B D

egyenes érintője a

T S H

háromszög körülírt körének.

Fehér Zsombor megoldása. Mindenekelőtt a

C H S ∢ - C S B ∢ = 90^{\circ}

feltételt fogjuk értelmezni. Ehhez vegyük fel az

A B

egyenesen azt az

X

pontot, melyre

S H X ∢

derékszög (1. ábra). Ekkor

C H X ∢ = C H S - 90^{\circ} = C S B ∢

. Tehát

C H X ∢ = C S X ∢

, így

C H S X

húrnégyszög. És mivel

S H X ∢ = 90^{\circ}

, ezért a Thalész-tétel alapján a

C H S X

kör középpontja

S X

felezőpontja, ami legyen

P

1. ábra

T S H

háromszög körülírt körének középpontját az

S H

és

T H

oldalak szakaszfelező merőlegesének metszéspontjaként fogjuk meghatározni (2. ábra).

S H

felezőmerőlegese ugyanaz, mint

S P H ∢

szögfelezője, hiszen

P S H

egyenlőszárú háromszög. Ezáltal az ábra már is sokat egyszerűsödött: csak vesszük

H C

felezőmerőlegesét, ez

P

-ben és

Q

-ban metszi

A B

-t és

A D

-t, majd tekintjük a

H P A ∢

és

H Q A ∢

szögfelezőjét (a belső szögfelezőt, mert az

S

és a

T

pont az

A P

, illetve az

A Q

szakasz belsejében helyezkedik el). Azt kell belátnunk, hogy ezek metszéspontja rajta van az

A H

szakaszon, hiszen ekkor

A H ⊥ B D

miatt

B D

valóban érinteni fogja a

T H S

k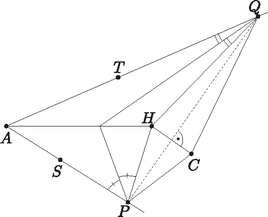ört.

2. ábra

Lemma. Tetszőleges

K L M N

négyszögre a

K

-ból és

M

-ből kiinduló belső szögfelezők pontosan akkor metszik egymást az

L N

átlón, mint amikor az

L

-ből és

N

-ből kiinduló szögfelezők a

K M

átlón.

Bizonyítás. A szögfelezőtétel alapján, ha a

K

M

szögfelezők mindketten az

O

pontban metszik

L N

-t, akkor

K L / K N = O L / O N = M L / M N

. Így

K L / M L = K N / M N

alapján az

L

N

szögfelezők ugyanolyan arányban osztják a

K M

szakaszt, azaz ugyanott metszik a

K M

átlót. Vagyis mindkettő pontosan akkor teljesül, ha a négyszög szemközti oldalainak szorzata egyenlő.
A lemmát alkalmazva az

A P H Q

négyszögre, azt kell belátnunk, hogy a

P A Q ∢

és

P H Q ∢

szögfelezője a

P Q

egyenesen metszi egymást.
Még nem használtuk a feladat

A B C ∢ = C D A ∢ = 90^{\circ}

feltételét (3. ábra). Ez alapján

A B C D

húrnégyszög, így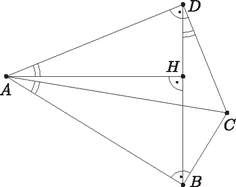

B A C ∢ = B D C ∢ = 90^{\circ} - A D H ∢ = H A D ∢

3. ábra

Megjegyzés. A feladat

B

és

D

pontját, illetve az ott lévő derékszögeket tulajdonképpen csak arra használjuk, hogy

B A C ∢ = H A D ∢

teljesüljön. Valójában a

C

pontot szabadon mozgathatjuk az

A C

egyenesen, az állítás érvényben marad.

Legyen az

A H C

kör és a

P Q

egyenes metszéspontja

E

(4. ábra). Mivel

H C

felezőmerőlegesén van

E

, a

H C

ív felezőpontja

E

, ezért

H A E ∢ = E A C ∢

. És mivel

Q A H ∢ = C A P ∢

, a

Q A P

szögfelezője nem más, mint

A E

. Az

A H C

kör középpontja rajta van

H C

felezőmerőlegesén,

P Q

-n, ezáltal a kör tükrös

P Q

-ra. Azon pontok halmaza, melyek

P

-től és

Q

-tól mért távolságainak aránya állandó, és ez az állandó

A P / A Q

, egy Apollóniusz-kör. Mégpedig egy olyan Apollóniusz-kör, ami átmegy

A

-n, és a szögfelezőtétel miatt

E

-n, emellett tükrös a

P Q

egyenesre. Így ez a kör csak az

A H C

kör lehet. Tehát

H

is rajta van az Apollóniusz-körön, így

H P / H Q = A P / A Q

, és

P H Q ∢

szögfelezője is átmegy

E

-n. Ezzel a feladat állítását bebizonyítottuk.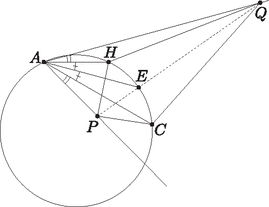

4. ábra

Megjegyzések. 1. Amennyiben az

A

H

C

pontok egy egyenesre esnek, az Apollóniusz-kör helyét egy felező merőleges veszi fel. Ebben az esetben az egész ábra szimmetrikus, a feladat állítása pedig triviális. Annak ellenére, hogy ráadásul a fenti bizonyítás is lényegében ugyanúgy működik, a versenyzők ezen megjegyzés hiányában ‐ mint minden speciális eset elmulasztásáért ‐ maximálisan 6 pontot kaphattak.
2. A megoldás utolsó lépésének alapja a következő egyszerű, de mégis meglepő tétel, amit érdemes lehet megjegyezni:

Tétel. Ha

A B C D

deltoid, akkor a

{P ∣ A P B ∢ \equiv D P C ∢ (mod 180^{\circ})}

halmaz, vagyis azon pontok mértani helye, melyekből az

A B

és

D C

szakaszok ugyanakkora irányított szögben látszanak, egy kör és egy egyenes (rombusz esetén két egyenes). A kör a fent látott Apollóniusz-kör, az egyenes pedig a deltoid szimmetriatengelye.

Ezt a tételt alkalmaztuk feladatunkban a

P H Q C

deltoidra: mivel

P A C ∢ = H A Q ∢

, ezért

A P / A Q = H P / H Q

, készen vagyunk. Ugyanakkor a tétel használatával pl. Lapunk B. 4448. feladata (2012. április) is könnyen adódik ‐ ezt Olvasónkra bízzuk, hogyan.

P

és

Q

A B C

hegyessszögű háromszög

B C

oldalszakaszán úgy helyezkednek el, hogy

P A B ∢ = B C A ∢

és

C A Q ∢ = A B C ∢

. Az

M

, illetve

N

pontok az

A P

, illetve

A Q

egyenesen úgy helyezkednek el, hogy

P

A M

szakasz felezőpontja és

Q

A N

szakasz felezőpontja. Bizonyítsuk be, hogy a

B M

és

C N

egyenesek az

A B C

háromszög körülírt körén metszik egymást.

Janzer Barnabás megoldása. Legyen a háromszög három oldala a szokásos jelölésekkel

a

b

és

c

. A

C A Q

és

C B A

háromszögek hasonlóak, mert a feladat feltételei miatt két megfelelő szögük azonos nagyságú. Így

\frac{A Q}{C A} = \frac{B A}{C B}

, vagyis

A Q = \frac{C A}{C B} \cdot B A = \frac{b c}{a}

. Ebből

A N = 2 \cdot \frac{b c}{a}

.
Legyen

H

B C

szakasz felezőpontja. Ekkor

B A H

és

A N C

háromszögek hasonlók, mivel egy szögük és a mellette lévő két oldal aránya azonos:

A B H ∢ = N A C ∢

, va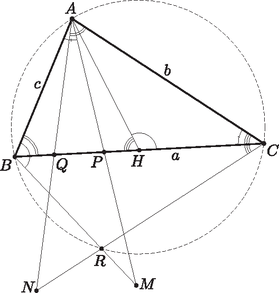lamint

\begin{matrix} \frac{B A}{B H} = \frac{c}{\frac{a}{2}} = \frac{2 c}{a} és \frac{A N}{A C} = \frac{2 \cdot \frac{b c}{a}}{b} = \frac{2 c}{a} . \end{matrix}

Így a hasonlóságból

A C N ∢ = B H A ∢

. Hasonlóan

A B M ∢ = A H C ∢

. Így ha a

B M

és

C N

egyenesek metszéspontja

R

A B R ∢ + R C A ∢ = A H C ∢ + B H A ∢ = 180^{\circ}

, így

A B R C

húrnégyszög, és ezt kellett belátni.

5. Minden pozitív egész

n

-re a Fokvárosi Bank

\frac{1}{n}

címletű érméket bocsát ki. Ha adott egy véges készlet ilyen (nem feltétlenül különböző címletű) érmékből, mely készletnek az összértéke legfeljebb

99 + \frac{1}{2}

, bizonyítsuk be, hogy a készletet feloszthatjuk

100

vagy kevesebb csoportra úgy, hogy minden csoportban az érmék összértéke legfeljebb

1

Di Giovanni Márk megoldása. Lássuk be a feladat általánosítását, azaz

n - \frac{1}{2}

összértékű érmékre és

n

dobozra, teljes indukcióval (

n = 100

-ra a feladat állítását kapjuk).

n = 1

-re az állítás triviális, mert az összes érmét berakhatjuk egyetlen dobozba.
Tegyük fel most, hogy

m - 1

-ig igaz az állítás (

m \geq 2

) és lássuk be

m

-re.
Ha van néhány érme, amelyek összértéke 1, akkor azokat berakhatjuk az első dobozba, ezzel visszavezetve az

m - 1

-es esetre, amit már beláttunk. Tehát mostantól feltehetjük, hogy nincsenek ilyen érmék.
Továbbá ha van kettő darab

1 / 2 t

értékű érménk, akkor azokat lecserélhetjük egy darab

1 / t

értékű érmére, mivel ha így el tudjuk végezni az elhelyezést, akkor az eredeti érméket is el tudjuk helyezni. Tehát feltehetjük, hogy minden páros nevezőjű érméből legfeljebb 1 darab van.
Rakjuk bele a dobozokba az érméket mohó algoritmussal, azaz vesszük a legnagyobb, addig nem elhelyezett érmét és belerakjuk az egyik dobozba (mint majd kiderül, lényegtelen, hogy melyikbe). Ha ezzel az algoritmussal sikerült elhelyezni az összes érmét, akkor készen vagyunk és az állítást beláttuk. Ha nem, akkor elakadtunk egy

\frac{1}{b}

értékű érménél. Eddig a dobozokban csak olyan érmék szerepelhetnek, amelyek legalább

1 / b

értékűek (a mohó algoritmus miatt). Továbbá minden dobozban a kimaradt hely kisebb mint

1 / b

, különben oda be tudnánk rakni még legalább egy kimaradt érmét. Legyen az üres hely mérete az

i

-edik dobozban

a_{i}

. Ekkor

\frac{1}{b} > {max}_{}^{} {a_{i}}

. Továbbá

\begin{matrix} (m - 1) \cdot {max}_{}^{} {a_{i}} \geq \sum a_{i} - {max}_{}^{} {a_{i}} > \sum a_{i} - \frac{1}{b} \geq \frac{1}{2} . \end{matrix}

Az utolsó egyenlőtlenség azért teljesül, mert az összes érme értékösszege legfeljebb

m - \frac{1}{2}

, így a dobozokban lévő érmék értékösszege meg az

1 / b

-s érmének az összege is legfeljebb

m - \frac{1}{2}

.
Ebből adódik:

\begin{matrix} {max}_{}^{} {a_{i}} > \frac{1}{m - 1} \cdot \frac{1}{2}, \end{matrix}

azaz

\frac{1}{b} > \frac{1}{2 m - 2}

, de mivel

b

egész, ezért

\frac{1}{b} \geq \frac{1}{2 m - 3}

.
Rakjuk bele az eddigi dobozokban lévő érméket értékeik szerint a következő táblázatba (egy mezőre akár több érme is kerülhet):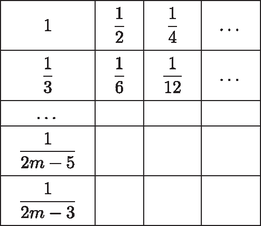

Nyilvánvalóan mivel

b \leq 2 m - 3,

ezért a táblázatba kerülő legkisebb elem legalább

\frac{1}{2 m - 3}

értékű.
Most nézzünk meg egy sort: az első mező kivételével minden mező nevezője páros, feltevésünk szerint tehát legfeljebb 1 érme lehet rajta. Vizsgáljuk meg az értékösszeget abban a sorban, ahol az első mező

\frac{1}{2 t - 1}

. A mezők összértéke az első mezőt leszámítva legfeljebb akkora, mint a mezőkön lévő számok összege (hiszen minden mezőn legfeljebb egy érme lehet). Ez az összeg pedig biztosan kisebb, mint annak a végtelen mértani sornak az összege, melynek első néhány eleme szerepel a mezőkön.
Tehát

\begin{matrix} összeg < \sum_{i = 1}^{\infty} \frac{1}{2 t - 1} \cdot \frac{1}{2^{i}} = \frac{1}{2 t - 1} \cdot \sum_{i = 1}^{\infty} \frac{1}{2^{i}} = \frac{1}{2 t - 1} . \end{matrix}

Az első mezőn legfeljebb

2 t - 2

darab érme lehet, különben ki lehetne választani közülük

2 t - 1

darabot, melyek összege 1. Így az értékösszeg a sorban biztosan kisebb, mint

\begin{matrix} (2 t - 2) \cdot \frac{1}{2 t - 1} + \frac{1}{2 t - 1} = 1. \end{matrix}

Mivel ezt a gondolatmenetet elvégezhetjük az összes sorra, ezért minden sorösszeg kisebb, mint 1. Mivel a táblázat

m - 1

darab sorból áll, így a táblázatban lévő érmék összértéke kisebb, mint

m - 1

. Innen

\begin{matrix} \sum a_{i} = m - \sum táblázat > m - (m - 1) = 1. \end{matrix}

Ekkor

{max}_{}^{} {a_{i}} > \frac{1}{m}

, azaz

\frac{1}{b} > \frac{1}{m}

.
Adjuk össze újra az érméket a táblázatos módszerrel, viszont most csak

1 / (m - 1)

-ig tartanak a sorok (vagy

1 / (m - 2)

-ig,

m

paritásától függően.)
Így a táblázatban lévő érmék értékösszege kisebb, mint

\frac{m}{2}

, azaz

\begin{matrix} \sum a_{i} = m - \sum táblázat > m - \frac{m}{2} = m / 2, azaz {max}_{}^{} {a_{i}} > \frac{1}{2}, \end{matrix}

azaz 1/b nagyobb, mint

1 / 2

. Ebből az következik, hogy

b = 1

, azaz egy 1 értékű érménél akadunk el. De korábban már feltettük, hogy semelyik néhány érmének az összege sem 1, így nincsen 1 értékű érménk sem, tehát ellentmondásra jutottunk.
Tehát a pakolással nem tudunk elakadni, azaz működik a módszer, így beláttuk

m

-re is. Ezzel beláttuk az indukciós lépést, így minden

n

-re igaz az állítás, azaz speciális esetként

n = 100

-ra is.

6. A sík egyeneseinek egy halmazát általános helyzetűnek nevezzük, ha közöttük nincs két párhuzamos egyenes, és semelyik három egyenesnek nincs közös pontja. Általános helyzetű egyenesek egy halmaza a síkot tartományokra bontja, amelyek közül némelyek véges területűek; ezeket az egyeneshalmaz véges tartományainak nevezzük.
Bizonyítsuk be, hogy minden elég nagy

n

-re teljesül az, hogy bármely,

n

általános helyzetű egyenesből álló halmaz egyenesei közül legalább

\sqrt[]{n}

egyenest kékre tudunk színezni úgy, hogy nincs olyan véges tartomány, aminek a határa teljesen kék.
Megjegyzés: Olyan megoldásokra is adható pont, amelyek az állítást

\sqrt[]{n}

helyett

c \sqrt[]{n}

-re bizonyítják; a pontszám a

c

konstans értékétől függ.

Ágoston Péter megoldása. Vegyük úgy, hogy az egyenesek kezdetben feketék, és jelentse egy egyenes pirosra színezése azt, hogy azt az egyenest már nem színezhetjük kékre.
Ekkor teljes indukcióval belátható, hogy minden

\sqrt[]{n}

-nél nem nagyobb

k

-ra ki lehet színezni

k

darab egyenest kékre úgy, hogy legfeljebb

k^{2} - k

darabot színeztünk pirosra, és minden két szomszédos kék oldallal rendelkező véges tartománynak van piros oldala.
Kezdőlépés: egy egyenest ki lehet így színezni, hiszen ekkor 0 egyenest kell pirosra színeznünk, mivel nyilvánvalóan nincs olyan véges tartomány, amelynek két szomszédos kék oldala lenne.
Indukciós lépés: ha

k - 1

egyenest már sikerült így kékre színezni, akkor kiszínezhetünk a feketék közül egy tetszőlegesen választott

k

-adikat is kékre és néhány alkalmasan választottat pirosra úgy, hogy a színezés megfeleljen az indukciós feltételnek. A pirosakat ugyanis elég úgy megválasztani, hogy az újonnan keletkezett szomszédos kék oldalpárú véges tartományoknak legyen ilyen oldala (a többire már biztosítva van), vagyis azoknak, amelyeknek az egyik oldala a szomszédos kékek közül az új kék egyenes. Vegyük fel az új kék egyenesnek a korábbi

k - 1

kék egyenessel vett metszéspontjaihoz egyik, illetve másik irányban legközelebb levő egyenes metszéspontjait, és amennyiben ezekben nem kék egyenes metszi az új kék egyenest, színezzük ezeket az egyeneseket pirosra (vagy hagyjuk meg annak) (1. ábra).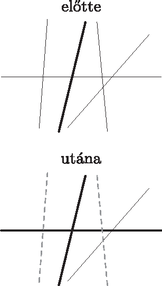

1. ábra

Ezzel legfeljebb

2 \cdot (k - 1) = 2 k - 2

egyenest színeztünk pirosra, és ,,szerencsés'' esetben biztosítottuk a feltétel teljesülését az összes olyan véges tartományra, amelynek a két szomszédos kék oldalegyenese között szerepel az új egyenes. Előfordulhat azonban, hogy a legszélső, kék egyenessel vett metszéspont a legszélső metszéspont is egyben, ekkor nincs mit kiszínezni azon az oldalon, de nem is kell, hiszen az ezen az oldalon levő tartományok nyilvánvalóan végtelenek. Az is előfordulhat, hogy két pirosra színezendő egyenes egybeesik (ha csak egy metszéspont van két kék egyenessel vett metszéspont között), de ezzel is csak megspórolunk egy pirosra színezést (2. ábra).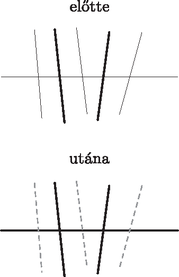

2. ábra

Ugyanakkor ha két kék egyenessel vett metszéspont szomszédos, akkor nem tudunk köztük semmit sem pirosra színezni, de így megspóroltunk két egyenesszínezést, amit a feltétel teljesítése érdekében még felhasználhatunk. Ennyi elég is, ugyanis ha a szomszédos kék egyenesek között levő, az új kék egyenessel mint oldallal rendelkező tartományok közül valamelyik véges, annak biztosan van piros vagy fekete oldala, hiszen ha csak kék lenne, lett volna eddig is két szomszédos kék oldala, így az indukciós feltétel szerint legalább egy piros is, ami ellentmondás. Ezt az oldalt tehát pirosra lehet színezni (vagy meghagyni annak) (3. ábra). (Az ábrákon a vastag vonal kék egyenest jelöl, a vékony vonal feketét, a szaggatott pedig pirosat.)

3. ábra

Tehát legfeljebb két egyenesszínezéssel ekkor is biztosítani lehet a két sokszögre a feltételt, vagyis összességében nem nőtt a pirosra színezett egyenesek száma, azaz továbbra is legfeljebb

2 k - 2

új piros egyenes keletkezett. Így mivel eddig legfeljebb

{(k - 1)}^{2} - (k - 1) = k^{2} - 2 k + 1 - k + 1 = k^{2} - 3 k + 2

egyenes volt piros, ezután legfeljebb

k^{2} - 3 k + 2 + 2 k - 2 = k^{2} - k

egyenes piros, és az indukciós feltételnek eleget tettünk.
Tehát amíg

k

nem haladja meg

\sqrt[]{n}

-et, tudunk olyan színezést, amely összesen legfeljebb

k^{2}

egyenest színez ki kékre vagy pirosra, és minden olyan véges tartomány, amelynek van két szomszédos kék oldala, rendelkezik piros oldallal is. Tehát ha kiszíneztünk

[\sqrt[]{n}]

egyenest kékre így, és

[\sqrt[]{n}] \neq \sqrt[]{n}

, akkor még van fekete egyenes, amelyet így nyugodtan kékre színezhetünk, hiszen a két szomszédos kék oldallal rendelkező véges tartományokból már nem csinálhat teljesen kék kerületű véges tartományt, és nyilvánvalóan a többiből sem. Így viszont kiszíneztünk legalább

\sqrt[]{n}

egyenest kékre (ha

[\sqrt[]{n}] = \sqrt[]{n}

, akkor is), és nincs csupa kék véges tartomány, vagyis az állítást beláttuk minden

n

-re.