| Cím: | Gráfalgoritmusok 1. | |
| Szerző(k): | Schmieder László | |
| Füzet: | 2015/október, 414 - 419. oldal |  PDF | MathML PDF | MathML |
| Hivatkozás(ok): | 2015/december: Gráfalgoritmusok 3.
2016/február: Gráfalgoritmusok 4. 2016/március: Gráfalgoritmusok 5. 2016/május: Gráfalgoritmusok 7. 2015/november: Gráfalgoritmusok 2. 2016/április: Gráfalgoritmusok 6. | |
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A gráfok sok hétköznapi probléma szemléltetésére és vizsgálatára alkalmasak. Ezekben a feladatokban a gráfok csúcsai például egy elemet, helyet, állapotot jelölnek, míg a gráf élei az egyes elemek közötti kapcsolatot, az állapotok közötti átmenetet mutatják. Ábrázolhatjuk például gráffal egy terület úthálózatát, ahol a csúcsok a városoknak és a közlekedési csomópontoknak felelnek meg, míg az utak az éleknek. Alkalmazhatjuk a gráfokat a sakkjáték menetének leírására is: a kezdőállásból elérhető összes állásnak megfeleltetünk egy-egy csúcsot, míg a szabályos lépéseknek a csúcsok közötti irányított éleket. 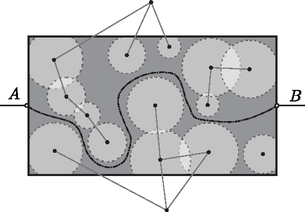 A kérdés eldöntése tehát azt igényli, hogy keressünk utat a gráf két lemezen kívüli csúcsa között. Ha kézzel, ceruzával kellene megoldani a feladatot egy papírra rajzolt gráfnál, akkor feltehetőleg megoldanánk a problémát; egy kisebb gráfon ránézésre, egy nagyobb gráfon némi ügyességgel. Ha az útkeresést egy számítógép végzi (mert pl. rendkívül nagy és bonyolult a gráf), akkor egy olyan műveletsorozatot kell megadnunk a számára, amely tetszőleges gráfon elvezet a kiinduló csúcstól a célba, vagy megadja, hogy a cél nem elérhető. Ez utóbbi választ persze csak akkor adhatja, ha a kiinduló csúcsból elérhető összes csúcsot már megvizsgálta, és azok között nem volt a cél. Általánosságban egy tetszőleges gráfban az útkereső algoritmus valamilyen sorrendben bejárja a start csúcsból elérhető teljes részét a gráfnak. Például a következő egyszerű eljárással: ha a start csúcs egyben nem a cél, akkor megnézi, hogy a start csúcsból közvetlenül elérhető csúcsok (szomszédok) között van-e a cél. Ha itt sem találja, akkor a szomszédok szomszédjait nézi meg, és így tovább. Ha eljutottunk közben a célig, akkor van út; ha pedig már nincs olyan él, amelyen új, még nem érintett csúcshoz érhetünk, akkor a keresés szintén véget ér, mert nincs út. A gráfok ilyen módszeres átvizsgálását leíró algoritmusokat a gráf bejárásának nevezzük. Vizsgáljuk meg, hogy milyen tudással rendelkezünk mi a gráf bejárásakor, és készítsünk ennek megfelelően algoritmust. Észrevehetjük, hogy a már egyszer megvizsgált csúcsokat úgy kerülhetjük el, ha valahogyan megjelöljük őket, pl. átszínezzük. Ezt a program is meg tudja tenni, pl. jelzi minden csúcsnál, hogy jártunk-e már ott. Kezdetben csak a start csúcs kap ilyen jelzést, a többi nem. Ezenkívül tudnunk kell, hogy egy csúcs szomszédjainak vizsgálata után melyik csúcson folytassuk a keresést. Az eddig megvizsgált részgráfot és a még nem érintett csúcsokat összekötő éleken kell továbbhaladnunk. Az így elérhető csúcsok egy-egy korábban elért csúcs szomszédjai. Tegyük azt, hogy minden új csúcs elérésekor följegyezzük a még meg nem látogatott szomszédokat. Kezdetben csak a start csúcs legyen a jegyzetben. A számítógép haladjon végig a följegyzett csúcsokon, vizsgálja meg, hogy elértük-e a célt, illetve bővítse a jegyzetet, amikor új szomszédokat talál. Legyen egy gráfban két csúcs távolsága az egyiktől a másikig vezető útvonalak közül a legkevesebb élen áthaladó út éleinek száma; illetve végtelen, ha nincs közöttük út. Ha a jegyzetünknek mindig a végére írunk, és az elejéről vesszük a következő vizsgálandó csúcsot, akkor először a start csúcsot érintjük (0 távolság), aztán az ő szomszédjait (a start csúcstól 1 távolság), majd ezek szomszédjait (2 távolság), és így tovább. A gráf csúcsait így a start csúcstól való távolságuk monoton növekvő sorrendjében érjük el. Ez azt jelenti, hogy a távolságban lévő csúcsok vizsgálata után kezdjük vizsgálni a távolságra lévő csúcsokat, tehát ez az algoritmus egyben a legrövidebb utat fogja megtalálni a start és a cél között (ha van út). Az algoritmus működése közben megjelöli a már meglátogatott csúcsokat. Kereséskor azok a csúcsok, amelyekben már jártunk, de még vannak nem érintett szomszédjai, egyfajta ,,határvonalat'' alkotnak a bejárt és nem bejárt csúcsok között. Ez a határ fokozatosan bővül, amikor a feljegyzésből egy újabb csúcsot megvizsgálunk. A keresés folyamatosan növeli a határ távolságát a kiinduló csúcstól, ugyanakkor a határvonal egyre hosszabb, mivel egyre több csúcs tartozik hozzá. Ezen tulajdonságok miatt a fent leírt útkereső algoritmust szélességi keresésnek nevezték el. jártunk(csúcsok start kivételével) := nem jártunk(start) := igen följegyzés := üres följegyzéshez fűz := start megvan_a_cél := hamis Ciklus amíg van följegyzés és nincs meg a cél csúcs := vegyük a következő csúcsot a följegyzésből Ha csúcs a cél akkor megvan_a_cél := igaz különben szomszéd := csúcs első szomszédja Ciklus amíg van szomszéd Ha nem jártunk(szomszéd) akkor följegyzéshez := szomszéd jártunk(szomszéd) := igaz Elágazás vége szomszéd := csúcs következő szomszédja Ciklus vége Elágazás vége Ciklus vége Szélességi keresés vége Az algoritmus befejeződésekor a megvan_a_cél nevű logikai változóból tudhatjuk meg, hogy sikerült-e utat találni. Ezzel gyakorlatilag megoldottuk a fémlap vezetésével kapcsolatos feladatot. Természetesen föl kell előtte építenünk a gráfot, azaz tudnunk kell, hogy mely csúcsok között van él. Mivel a feladatban legföljebb 100 körről van szó (és kell még két csúcs a körökön kívül), ezért megtehetjük, hogy fölveszünk egy -es táblázatot, amelynél az 5. sor 16. oszlopában lévő érték jelzi, hogy az 5. és 16. gráfcsúcs között van-e él. Mivel a kapcsolat itt szimmetrikus, azaz a gráf nem irányított, így nyilván ugyanez az érték szerepel a 16. sor 5. oszlopában. Legyen például 0, ha nincs él és 1, ha van él. A feladatban logikai értékek is állhatnának a táblázatban, de a későbbiek miatt maradjunk mégis a számoknál. Az így létrejövő táblázatot a gráf szomszédsági mátrixának hívjuk. A mátrix kitöltése geometriai számításokkal történhet a körök sugarai és koordinátái, valamint a fémlap méretei alapján. Ha egy másik feladatban az útról többet is szeretnénk megtudni, például hogy milyen hosszú, illetve hogy mely csúcsokon halad keresztül, akkor bővítenünk kell az algoritmust. Keresés közben még nem tudhatjuk, hogy azok közül az élek közül, amelyeken áthaladunk, melyek lesznek benne az útban, tehát nem tudjuk megadni az utat. De bármely csúcs elérésekor tudjuk, hogy honnan értünk az adott csúcsba, ezért ha ezt az információt megőrizzük, akkor a cél csúcsból visszafelé kiolvasható a start csúcsig az út. Ehhez vegyünk föl minden csúcshoz egy értéket, amely megadja, hogy melyik csúcsból érkeztünk ide. Ha egy csúcsot nem értünk el, vagy az a start csúcs (ahová nem érkezünk sehonnan), akkor az érték jelentse azt, hogy nincs a keresés során megelőző csúcs. Ha a csúcsokat pl. 1-től sorszámozzuk, akkor legyen ez az érték . Nézzük meg a szélességi keresés algoritmusának megvalósítását abban az esetben, ha szeretnénk megkapni a keresés által talált utat. Legyenek a gráf csúcsai -től -ig sorszámozottak, és legyen adott egy -es szomszédsági mátrix. Szükségünk van még két méretű tömbre, melyek keresés közben megmutatják, hogy mely csúcsokban jártunk és hogy az adott csúcsot melyik szomszédjából értük el, illetve egy olyan jegyzetfüzetre, amely segítségével sorra vehetjük a csúcsokat. Ez utóbbihoz egy sor elnevezésű adatszerkezet a leghasznosabb, amelynek a végére tudunk írni és az elejéről tudjuk kiolvasni az elemeket. Könnyen megvalósítható egy tömb és néhány egész változó segítségével. Legyen egy eleje, vége, fhely és darab változó, amely megadja, hogy hol van a tömbben a sor első és utolsó eleme, mennyi a férőhely és most hány elem van a sorban. A sor szokásos műveletei: a végére fűzés és az elejéről való olvasás (ami most egyben az elem eltávolítása is a sor elejéről), valamint annak vizsgálata, hogy a sor üres-e. A kezdetben üres sornál legyen a darab és vége értéke nulla, az eleje pedig egy. A sorba történő befűzés algoritmusa ekkor a következő: Sorba(elem) Ha darab<fhely akkor vége := vége + 1 Ha vége = fhely akkor vége := 1 s[vége] := elem különben Hiba: nincs több hely a sorban Elágazás vége Sorba vége A sor elejének olvasása és az üresség vizsgálatát végző algoritmusok sem bonyolultabbak. Ha mindezekkel készen vagyunk, akkor a szélességi keresés ‐ kiegészítve az útvonal megjegyzésével ‐ a következőképp néz ki ( a gráf csúcsainak száma és a gráf szomszédsági mátrixa): Szélességi keresés útvonallal(gráf, start, cél) Ciklus i := 1-től N-ig jártunk[i] := hamis honnan[i] := -1 Ciklus vége Sor_legyen_üres Sorba(start) jártunk[start] := igaz megvan_a_cél := hamis Ciklus amíg nem üres a sor és nem igaz megvan_a_cél Sorból(csúcs) Ha csúcs = cél akkor megvan_a_cél := igaz különben Ciklus szomszéd := 1-től N-ig Ha m[csúcs][szomszéd] = 1 és nem jártunk[szomszéd] akkor Sorba(szomszéd) jártunk[szomszéd] := igaz honnan[szomszéd] := csúcs Elágazás vége Ciklus vége Elágazás vége Ciklus vége Szélességi keresés útvonallal vége 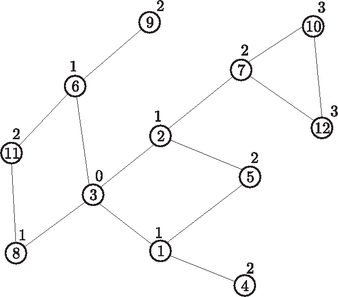 A példaként mellékelt gráfban utat keresünk a 3-as számú csúcstól a 12-es számú csúcsig. A gráfon jelöltük a csúcsok fölött a csúcs start csúcstól vett távolságát is. A sor elemeit tároló tömb állapota keresés közben egy adott pillanatban a következő: Amennyiben a szélességi keresés algoritmusából kihagyjuk a cél csúcs vizsgálatát, akkor egy olyan algoritmust kapunk, amely bejárja a start csúcsból elérhető részét a gráfnak. Ha az (irányítatlan) gráf összefüggő, akkor a teljes gráfot. A cél vizsgálata nélküli szélességi keresés választ ad arra a kérdésre, hogy egy (irányítatlan) gráf összefüggő-e: ha minden csúcsban jártunk, akkor az. Az út megkeresésére a most választott módszertől lényegesen eltérő módszerek is vannak. Próbáljunk meg például kijutni egy labirintusból! Ez a probléma is visszavezethető gráfban út keresésére. Legyen a labirintus járatainak végein és a járatok kereszteződésében egy-egy csúcs a labirintusnak megfeleltethető gráfban, a járatok pedig természetesen legyenek az élek. Induljunk el a labirintus egy pontjáról. A szélességi keresés megtalálja ugyan a kijárathoz vezető legrövidebb utat, de a sorból kivett csúcsok sokszor egészen távol vannak egymástól, ezért a valóságban túl sok fölösleges mozgást jelentenek. Sokkal természetesebb megoldás, hogy elindulunk sorrendben az első bal kézre eső járaton, és ha kiértünk, minden rendben, ha zsákutcába jutottunk, akkor visszamegyünk, és ha kereszteződéshez jutottunk, akkor ott is elindulunk a balra eső első járaton, és így tovább. Ha egy sikertelen keresés után visszaérünk egy kereszteződéshez, akkor ott a következő járaton elindulva végezzük az előbbi lépéseket. Ez az algoritmus is megtalál egy cél csúcsot a start csúcsból indulva, de egészen más csúcsokat és éleket érint. Mivel a gráf bejárásának ez a módja olyan, hogy hosszan előremegy a bal első éleken, vagyis elég hamar a start csúcstól távolra jut, ezért mélységi keresésnek nevezték el. Az algoritmus részleteivel a cikk folytatásában foglalkozunk. 1. Mit jelentenek a sakkot leíró gráfban a kimenő él nélküli csúcsok? Van-e a gráfban kör? 2. Hogyan módosítsuk a szélességi keresést úgy, hogy ne a start csúcstól vezető legrövidebb utakat, hanem csak azok hosszát adja meg minden elérhető csúcsra? 3. Legalább mekkora méretű sorra van szükség egy csúcsból álló gráfban a szélességi keresés közben? Adjunk meg egy gráfot, start és cél csúcsot, amelynél tényleg kell ekkora méretű sor! 4. Tekintsük egy gráf azon részét, amelyet a szélességi keresés érint egy adott csúcsból, vagyis az érintett csúcsokat és a hozzájuk vezető éleket. Lehet-e ebben a gráfban kör? 5. Szeretnénk egy gráf csúcsait kiszínezni két színnel úgy, hogy minden csúcsot kiszínezünk, és a szomszédos csúcsokat mindig különböző színűre festjük. Ez nyilván nem lehetséges bármely gráfban. Módosítsuk úgy a szélességi bejárást, hogy elvégezze a színezést, ha az lehetséges! |