Cím:	Megoldásvázlatok a 2015/6. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Lorántfy László
Füzet:	2015/október, 402 - 408. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Egy közvélemény-kutatás kérdéseire az első hónapban $700$ ember válaszolt, mindenki pontosan egyet választott a felkínált három lehetőségből. A feleletek aránya $4:7:14$ volt. Ezután még néhány ember részt vett a közvélemény-kutatásban, így a feleletek aránya $6:9:16$ lett. Legkevesebb hány ember válaszolt utólag a kérdésekre? Ebben az esetben végül melyik lehetőséget hányan választották?  (11 pont)   Megoldás. A 700 ember válaszát arányosan elosztva a lehetőségeket először 112, 196, 392 ember választotta. A második esetben az arányszámok összege 31, így gondolhatnánk, hogy a 700-at követő 31-el osztható szám megfelelő lesz. Ez a 713. Ezt arányosan elosztva 138, 207, 368 jön ki a lehetőségeket választók számára. Ez azonban nem lehetséges, mert a harmadik lehetőséget választók száma csökkenne ez előző esethez képest. Tehát keressük a legkisebb, 392-nél nagyobb 16-al osztható számot. Ez a $400=25\cdot 16$. Így a végső szavazók száma legkevesebb $25\cdot 31=775$. Tehát legkevesebb 75 ember válaszolt utólag és ekkor az adott lehetőségeket 150, 225 és 400 ember választotta.   2. A mosogatógépünkön háromféle program van. Egy mosogatáshoz az $A$ program $30\%$-kal több elektromos energiát, viszont $20\%$-kal kevesebb vizet használ, mint a $B$ program. A $B$ program $15\%$-kal kevesebb elektromos energiát és $25\%$-kal több vizet használ egy mosogatáshoz, mint a $C$ program. Mindhárom program futtatásakor 50 Ft-ba kerül az alkalmazott mosogatószer. Egy mosogatás az $A$ programmal 165 Ft-ba, a $B$ programmal 150 Ft-ba kerül. Mennyibe kerül a $C$ programmal egy mosogatás?  (12 pont)   Megoldás. A $B$ program $x$ Ft értékű elektromos energiát és $y$ Ft értékű vizet használ egy mosogatás alkalmával: $x+y+50=150$. Az $A$ program $1\mathrm{,}3x$ Ft értékű elektromos energiát, és $0\mathrm{,}8y$ Ft értékű vizet használ egy mosogatás alkalmával. A költségre vonatkozó egyenlet: $1\mathrm{,}3x+0\mathrm{,}8y+50=165$. A következő egyenletrendszert kapjuk $x$-re és $y$-ra: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x+y}& {\displaystyle =\mathrm{100,}}\hfill \\ \hfill {\displaystyle 1\mathrm{,}3x+0\mathrm{,}8y}& {\displaystyle =115.}\hfill \end{array}}$ Az egyenletrendszer megoldása: $x=70$, $y=30$. A feltételek alapján a $C$ program futtatása során az elektromos energia ára: $x/0\mathrm{,}85\approx 82$ Ft, a víz ára: $y/1\mathrm{,}25=24$ Ft. A mosogatószer árát is figyelembe véve a $C$ programmal egy mosogatás $82+24+50=156$ Ft-ba kerül.   3. Hányféleképpen húzhatunk ki a $32$ lapos magyar kártyából $6$ lapot úgy, hogy legyen köztük pontosan két piros, két zöld és két ász?  (14 pont)   Megoldás. 1. eset: A két ász éppen a piros és a zöld ász. Ekkor még egy piros lapot kell választanunk a maradék 7 piros közül, egy zöldet a maradék 7 zöld közül és 2 lapot a nem piros, nem zöld és nem ász 14 lap közül. Az esetek száma: $\begin{array}{c}{\displaystyle N_1=\left(\genfrac{}{}{0ex}{}{7}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{7}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{14}{2}\right)=7\cdot 7\cdot \frac{14\cdot 13}{2}=4459.}\end{array}$ 2. eset: Az egyik ász a piros ász, a másik nem a zöld ász. Ekkor kell egy ászt választanunk a másik két ász közül, majd egy piros lapot a maradék 7 piros közül, két zöld lapot a nem ász 7 zöld közül és még egy lapot a nem piros, nem zöld és nem ász 14 lap közül. Az esetek száma: $\begin{array}{c}{\displaystyle N_2=2\cdot \left(\genfrac{}{}{0ex}{}{7}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{7}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{14}{1}\right)=2\cdot 7\cdot \frac{7\cdot 6}{2}\cdot 14=4116.}\end{array}$ 3. eset: Az egyik ász a zöld ász, a másik nem a piros ász. $N_3=N_2=4116$. 4. eset: A makk és a tök ászt választjuk. Ekkor kell még 2 piros lapot választanunk a nem ász 7 piros közül, 2 zöld lapot pedig a nem ász 7 zöld közül. Az esetek száma: $\begin{array}{c}{\displaystyle N_4=\left(\genfrac{}{}{0ex}{}{7}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{7}{2}\right)=\frac{7\cdot 6}{2}\cdot \frac{7\cdot 6}{2}=441.}\end{array}$ Az összes esetek száma: $N=N_1+N_2+N_3+N_4=4459+2\cdot 4116+441=13132$.   4. Egy kecske egy kerítéssel védett $10\times 3$ m-es virágágy körüli, elegendően nagy réten legel. A kecskét 16 m hosszú kötéllel a kerítés $10$ méteres oldalának felezőpontjánál levert cölöphöz kötötték. Mekkora területen legelheti le a füvet a kecske? Hányadrészére csökken ez a terület, ha a kötél hosszát $10$ méterre csökkentik?  (14 pont)   Megoldás. A 16 méteres kötél esetén a lelegelhető terület egy 16 m sugarú félkörből és két-két 11 és 8 m sugarú negyed körből áll. A virágágyás mögött a 8 m sugarú negyed körök átfedik egymást (1. ábra). Ezt a területet duplán számoljuk a fél és negyed körök területének összegzésekor, tehát egyszer le kell vonni. A keletkező $JKL$ idomot egy egyenes szakasz és két körív határolja. Állítsunk merőlegest az $L$ pontból a $JK$ szakaszra. A merőleges szakasz $M$ talppontja a $JK$ szakasz és az $AD$ szakasz felezőpontja lesz. Így két egybevágó fél körszelet jött létre. A fél körszelethez tartozó középponti szögre a $DML$ derékszögű háromszögben: $\text{cos}\alpha =5/8$, amiből $\alpha \approx 51\mathrm{,}{32}^{\circ }$. A két fél körszeletből egy egész körszeletet összeállítva a 8 cm sugarú körben, a hozzá tartozó körcikk középponti szöge: 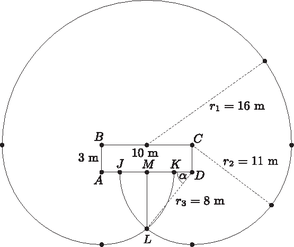$2\alpha \approx \mathrm{102,}{64}^{\circ }$.   1. ábra   A körszelet területe, amit majd le kell vonnunk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_{\text{szelet}}}& {\displaystyle =T_{\text{cikk}}-T_{▵}=\frac{8^2\pi }{{360}^{\circ }}\cdot 102\mathrm{,}{64}^{\circ }-\frac{8^2\text{sin}\left({102\mathrm{,}64}^{\circ }\right)}{2}\approx 57\mathrm{,}32-31\mathrm{,}22=26\mathrm{,}1{\text{m}}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle T_{16}}& {\displaystyle =\frac{\left({16}^2+{11}^2+8^2\right)\cdot \pi }{2}-T_{\text{szelet}}\approx 692\mathrm{,}72-26\mathrm{,}1=666\mathrm{,}62{\text{m}}^2\mathrm{.}}\hfill \end{array}}$ A megrövidített, 10 m hosszú kötél esetén (2.ábra): 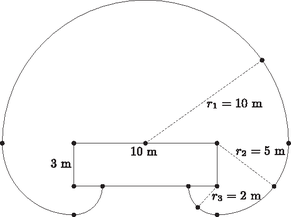${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_{10}}& {\displaystyle =\frac{\left({10}^2+5^2+2^2\right)\cdot \pi }{2}=64\mathrm{,}5\pi \approx 202\mathrm{,}6{\text{ m}}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{T_{10}}{T_{16}}}& {\displaystyle =\frac{202\mathrm{,}6{\text{m}}^2}{666\mathrm{,}62{\text{m}}^2}\approx 0\mathrm{,}304.}\hfill \end{array}}$   2. ábra   A lelegelhető terület közel 30%-ára csökken a kötél lerövidítésével.   II. rész     5. Oldjuk meg az alábbi egyenletet: $\begin{array}{c}{\displaystyle \text{log}{}_4\left(4\text{sin}{}^{2}2x\right)=2-\text{log}{}_2\left(-2\text{tg}x\right)\mathrm{.}}\end{array}$ (16 pont)   Megoldás. $\text{sin}2x=2\text{sin}x\text{cos}x\ne 0$ és $\text{tg}x<0$ esetén átalakítva az egyenlet bal, majd jobb oldalát: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{log}{}_4\left(4\text{sin}{}^{2}2x\right)}& {\displaystyle =\frac{\text{log}{}_2\left(4\text{sin}{}^{2}2x\right)}{\text{log}{}_{2}4}=\frac{\text{log}{}_2\left(4\text{sin}{}^{2}2x\right)}{2};}\hfill \\ \hfill {\displaystyle 2-\text{log}{}_2\left(-2\text{tg}x\right)}& {\displaystyle =\text{log}{}_{2}4-\text{log}{}_2\left(-2\text{tg}x\right)=\text{log}{}_2\frac{4}{-2\text{tg}x}\mathrm{.}}\hfill \end{array}}$ Ezután az egyenlet: $\begin{array}{c}{\displaystyle \frac{\text{log}{}_2\left(4\text{sin}{}^{2}2x\right)}{2}=\text{log}{}_2\frac{4}{-2\text{tg}x}\mathrm{,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle \text{log}{}_2\left(4\text{sin}{}^{2}2x\right)=\text{log}{}_2{\left(\frac{2}{-\text{tg}x}\right)}^2\mathrm{.}}\end{array}$ Mivel a $\text{log}{}_{2}x$ függvény szigorúan monoton növekvő, így $\begin{array}{c}{\displaystyle 4\text{sin}{}^{2}2x={\left(\frac{2}{-\text{tg}x}\right)}^2\mathrm{,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle 4\cdot 4\text{sin}{}^{2}x\text{cos}{}^{2}x=\frac{4\text{cos}{}^{2}x}{\text{sin}{}^{2}x}\mathrm{,}\text{és így}4\text{sin}{}^{4}x\text{cos}{}^{2}x=\text{cos}{}^{2}x\mathrm{.}}\end{array}$ Mivel $\text{cos}x\ne 0$, ezért $4\text{sin}{}^{4}x=1$, vagyis $\text{sin}{}^{2}x=\frac{1}{2}$, amiből $\text{sin}x=\pm \frac{\sqrt[]{2}}{2}$. Mivel $\text{tg}x<0$, ezért a megoldás $x=-\frac{\pi }{4}+k\pi$, ahol $k\in \text{Z}$.   6. Mennyi annak a valószínűsége, hogy a hatoslottó húzáson a $45$ számból (visszatevés nélkül) $6$-ot kihúzva, a hat lottószámot növekvő sorrendbe rakva egy számtani sorozat egymást követő tagjait kapjuk?  (16 pont)   Megoldás. Az összes lehetséges eset száma $C_{45}^6=\left(\genfrac{}{}{0ex}{}{45}{6}\right)=8145060$. Kedvező eset az, ahol a kihúzott számokat növekvő sorrendbe rendezve azok a következő alakúak: $a$, $a+r$, $a+2r$, $a+3r$, $a+4r$, $a+5r$, ahol $a\mathrm{,}r\in {\text{N}}^{+}$, $a\le 40$, $r\le 8$. Az $a$ lehetséges értékei $r=1$ esetén $\mathrm{1,2,}\text{...}\mathrm{,40}$; $r=2$ esetén $\mathrm{1,2,}\text{...}\mathrm{,35}$; $r=3$ esetén $\mathrm{1,2,}\text{...}\mathrm{,30}$; $\text{...}$; $r=8$ esetén $\mathrm{1,2,3,4,5}$. Összesítve a kedvező eseteket: $40+35+30+\text{...}+5=\frac{40+5}{2}\cdot 8=180$ eset. Tehát a valószínűség: $\begin{array}{c}{\displaystyle p=\frac{180}{8145060}\approx 2\mathrm{,}210\cdot {10}^{-5}\mathrm{.}}\end{array}$   7. Milyen görbét ír le az $y=x^2-2\left(m-3\right)x+m-8$ parabola csúcsa, ha az $m$ paraméter értéke végigfut a valós számok halmazán? Az $m$ paraméter mely értékénél lesz a csúcs ordinátája maximális? Adjuk meg ebben az esetben a parabola $P\left(0;-5\right)$ ponton átmenő érintőinek egyenletét.  (16 pont)   Megoldás. $\begin{array}{c}{\displaystyle y=x^2-2\left(m-3\right)x+m-8={\left(x-\left(m-3\right)\right)}^2-{\left(m-3\right)}^2+m-8.}\end{array}$ A parabola csúcsa $x=m-3$-nál van, ordinátája ekkor $y=-{\left(m-3\right)}^2+m-8=-{\left(m-3\right)}^2+\left(m-3\right)-5$, vagyis a csúcs az $y=-x^2+x-5$ egyenletű parabolán fog mozogni. Az $\begin{array}{c}{\displaystyle y=-x^2+x-5=-{\left(x-\frac{1}{2}\right)}^2-4\frac{3}{4}}\end{array}$ függvény maximuma $x=\frac{1}{2}$-nél van, értéke $y=-4\frac{3}{4}$. Tehát a parabola csúcsa $x=m-3=\frac{1}{2}$, azaz $m=3\mathrm{,}5$ esetén lesz a legmagasabban. 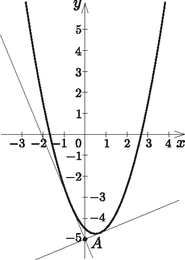  3. ábra   Az érintő egyenlete $y=kx-5$ alakú. A parabola egyenlete $y=x^2-x-4\mathrm{,}5$. Keressük a $k$ paraméter értékeit, ha az egyenes a parabola érintője. Ez akkor lesz, ha az egyenesnek és a parabolának egy közös pontja van. $\begin{array}{c}{\displaystyle kx-5=x^2-x-4\mathrm{,}\mathrm{5,}\text{vagyis}{x}^2-\left(1+k\right)x+0\mathrm{,}5=0.}\end{array}$ A másodfokú egyenlet diszkriminánsa: $D={\left(1+k\right)}^2-2=0$, amiből ${\left(1+k\right)}^2=2$, vagyis $1+k=\pm \sqrt[]{2}$. Így $k_1=\sqrt[]{2}-1$ és $k_2=-\sqrt[]{2}-1$ a két lehetséges érték. Tehát az érintők egyenlete: $\begin{array}{c}{\displaystyle y=\left(\sqrt[]{2}-1\right)x-5\text{és}y=\left(-\sqrt[]{2}-1\right)x-5\text{(<span style="font-style: italic;">3. ábra</span>).}}\end{array}$   8. Az azonos tengerszint feletti magasságban fekvő Hencida és Boncida között a távolság 5 km. Hencidából egy közeli hegy csúcsa $30{}^{\circ }$-os, Boncidából pedig $11{}^{\circ }$-os szög alatt látszik. Hencidából a hegy csúcsát és Boncidát összekötő szakasz látószöge ${120}^{\circ }$-os. $a)$ Milyen magas a hegy? $b)$ A két várost összekötő szakasz felénél elindítanak egy távirányításos repülőgép modellt, ami végig a szakaszfelező merőleges síkjában mozog. Mennyire közelítheti meg repülés közben a hegy csúcsát?  (16 pont)   Megoldás. $a)$ A 4. ábra jelöléseit használjuk. Legyen $x$ a hegy magassága. A $CTH$ és $CTB$ derékszögű háromszögekben $\text{sin}{30}^{\circ }=\frac{x}{a}$, illetve $\text{sin}{11}^{\circ }=\frac{x}{b}$, ebből $a=2x$ és $b=\frac{x}{\text{sin}{11}^{\circ }}\approx 5\mathrm{,}24x$. A $CHB$ háromszögben felírhatjuk a koszinusztételt a $b$ oldalra, majd behelyettesítjük az előbb kapott összefüggéseket: $b^2=a^2+5^2-2\cdot a\cdot 5\cdot \text{cos}{120}^{\circ }$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(5\mathrm{,}24x\right)}^2}& {\displaystyle ={\left(2x\right)}^2+25-2\cdot 2x\cdot 5\cdot \left(-0\mathrm{,}5\right)\mathrm{,}\text{ebből}}\hfill \\ \hfill {\displaystyle 27\mathrm{,}4576x^2}& {\displaystyle =4x^2+25+10x\mathrm{,}\text{bal oldalra rendezve}}\hfill \\ \hfill {\displaystyle 23\mathrm{,}4576x^2-10x-25}& {\displaystyle =0.}\hfill \end{array}}$ Az egyenletet megoldva és a magasságra kapott negatív megoldást elvetve: $x=1\mathrm{,}2673$. Tehát a hegy magassága (ahhoz a tengerszint feletti magassághoz képest, ahol Hencida és Boncida is fekszik) kb. 1267 m. 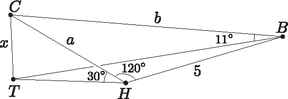  4. ábra   $b)$ Az 5. ábra jelöléseit használjuk. A legkisebb távolság esetén a repülőgép ($R$) rajta van a $HB$ szakasz $\text{S}$ felező merőleges síkján, a hegy csúcsának magasságában. A keresett távolság $CR$. Ennek a vízszintes szakasznak a vízszintes síkra eső merőleges vetülete $TN$, amely a $TNFH$ derékszögű trapéz hosszabbik alapja lesz. A 4. ábra szerint $\begin{array}{c}{\displaystyle TH=\frac{x}{\text{tg}{30}^{\circ }}\approx 2\mathrm{,}195\text{és}TB=\frac{x}{\text{tg}{11}^{\circ }}\approx 6\mathrm{,}520.}\end{array}$ Jelölje a $TN$ szakaszon $P$ azt a pontot, amelyre $PHB\sphericalangle ={90}^{\circ }$, és legyen $\alpha =THP\sphericalangle$. A $THB$ háromszögben a koszinusz tétel alapján $\begin{array}{c}{\displaystyle 6\mathrm{,}{520}^2=2\mathrm{,}{195}^2+5^2-2\cdot 5\cdot 2\mathrm{,}195\cdot \text{cos}\left(\alpha +{90}^{\circ }\right)\mathrm{,}}\end{array}$ amiből $\text{cos}\left(\alpha +{90}^{\circ }\right)\approx -0\mathrm{,}5782$, azaz $\alpha +{90}^{\circ }\approx {125\mathrm{,}32}^{\circ }$, vagyis $\alpha \approx {35\mathrm{,}32}^{\circ }$. A $TPH$ derékszögű háromszögben: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle TP}& {\displaystyle =TH\cdot \text{sin}\alpha \approx 2\mathrm{,}195\cdot 0\mathrm{,}5777\approx 1\mathrm{,}\mathrm{268,}}\hfill \\ \hfill {\displaystyle RC}& {\displaystyle =TN=TP+PN=1\mathrm{,}268+2\mathrm{,}5=3\mathrm{,}768.}\hfill \end{array}}$ Tehát a repülőgép a hegycsúcsot kb. 3768 méterre közelítheti meg.   5. ábra     9. János egy vízzel teli hordó aljára 4 mm átmérőjű lyukat fúrt és a kifolyó víz sebességét vizsgálta. A Bernoulli-egyenletből levezette, hogy $v=\sqrt[]{2gx}$, ahol $x$ a vízszint pillanatnyi magassága. Megmérte, hogy a teli hordóból az első másodpercben 62,8 cm${}^3$ víz folyt ki. (A sebességet itt állandónak vehetjük, a rövid mérési idő miatt.) Ezután megállapította, hogy $5$ perc alatt pontosan 10 cm-rel csökkent a vízszint. Feltételezzük, hogy a vízszint exponenciálisan csökken az $x=h\cdot 2^{-t/T}$ függvény szerint, ahol $h$ a kezdeti vízszint magassága, $T$ pedig a hordóban lévő víz ,,felezési ideje''. A hordót üresnek tekinthetjük, ha már csak 1 cm magas a vízszint benne. A teli állapotból mennyi idő alatt ürül ki a hordó?  (16 pont)   Megoldás. A lyuk átmérője $d=4$ mm, sugara $r=2\text{ mm}=0\mathrm{,}2\text{ cm}$. Keresztmetszete $A=r^2\pi =0\mathrm{,}{2}^2\pi \approx 0\mathrm{,}1257{\text{cm}}^2$. A $t=1$ sec alatt kifolyó vízmennyiség $V=Avt$, amiből a sebesség $\begin{array}{c}{\displaystyle v=\frac{V}{At}=\frac{\mathrm{62,8}{\text{cm}}^3}{0\mathrm{,}1257{\text{cm}}^2\cdot 1\text{sec}}\approx 499\mathrm{,}6\frac{\text{cm}}{\text{sec}}\approx 5\frac{\text{m}}{\text{s}}\mathrm{.}}\end{array}$ A $v=\sqrt[]{2gx}$ képletből kiszámíthatjuk a hordóban lévő víz kezdeti magasságát: $\begin{array}{c}{\displaystyle h=\frac{v^2}{2g}=\frac{5^2}{2\cdot 10}=1\mathrm{,}25\text{m}=125\text{cm}\mathrm{.}}\end{array}$ A vízszint 5 perc alatt 10 cm-rel csökken, így $t=300$ sec esetén $x=115$ cm. Ezeket behelyettesítve a képletbe a felezési idő meghatározható: $115=125\cdot 2^{-300/T}$, amiből $\begin{array}{c}{\displaystyle T=\frac{-300\cdot \text{lg}2}{\text{lg}\frac{115}{125}}=2494\text{ sec}\approx 41\mathrm{,}6\text{perc}\mathrm{.}}\end{array}$ $T$ ismeretében kiszámítható az $x=1$ cm vízmagassághoz tartozó idő, ami a hordó kiürülését jelenti: $1\text{cm}=125\text{cm}\cdot 2^{-t/2494}$, amiből $\begin{array}{c}{\displaystyle t=\frac{-2494\cdot \text{lg}\frac{1}{125}}{\text{lg}2}\approx 17373\text{sec}=\text{4 óra 49 perc 33 sec}}\end{array}$ alatt ürül ki a hordó.