Kezdőlap


Cím:	Rajzoljuk meg a másik metszéspontot is!
Szerző(k):	Kós Géza
Füzet:	2015/október, 395 - 399. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jótanács: Ha egy feladat egy kör és egy egyenes, vagy két kör egy bizonyos metszéspontját kéri, akkor rajzoljuk meg a bizonyítandó állítást a másik metszésponttal is, és vizsgáljuk a kétféle esetet egyszerre, ugyanazon az ábrán.

Két példát szeretnék mutatni arra, hogy ez az elv hogyan használható versenyfeladatok megoldásában. Mindkét példa a Nemzetközi Matematikai Diákolimpián szerepelt. Az elsőt, amit a nemzetközi zsűri közepes nehézségű feladatnak szánt, a közel száz országból válogatott 548 versenyző közül csak 86 tudta megoldani ‐ ennyien kapták meg a maximális 7 pontot ‐, és további 7 kapott 6-ot vagy 5-öt. (A magyar csapat összesen

1 + 1

pontot szerzett.) A másik példa az idei 3. feladat, ezt az 577 versenyő közül 30 oldotta meg kifogástalanul, és még egyvalaki kapott 6 pontot. (A magyarok közül négyen kaptak egy-egy pontot.)

Gondoljuk meg, hogy mi is van a Jótanács mögött. Képzeljük el, hogy egy feladatot, ahol valamilyen geometriai egybeesést (pl. három egyenes egy ponton megy át) kell bizonyítani, koordinátákkal oldunk meg. Először különböző betűket választunk a szabadon megválasztható paraméterek, például a különböző pontok koordinátáinak jelölésére, utána pedig ezekkel a betűkkel kifejezzük a korábbiaktól függő pontok koordináit és a különböző görbék, egyenesek egyenleteiben szereplő együtthatókat. Ha pontosan számolunk, a végén a bizonyítandó állítás egy algebrai azonosság kell, hogy legyen.
Kör és egyenes, illetve két kör metszéspontjának kiszámításához másodfokú egyenletet kell megoldanunk. Az eredmény egy gyökös kifejezés lesz: a metszéspont koordinátáiban megjelenik egy kellemetlen négyzetgyök (a másodfokú egyenlet két gyökének különbsége), amit azután magunkkal kell cipelnünk. A megoldás végén egy négyzetgyökös azonosságot kell ellenőriznünk. Itt jön a lényeg. Tapasztalhattuk, hogy a négyzetgyökös azonosságok többnyire akkor is igazak maradnak, ha a pozitív négyzetgyök helyett a negatívat vesszük; ezért a legtöbb esetben a bizonyítandó állítás a másik metszésponttal is igaz. Az is előfordul, hogy egy feladaton belül több ilyen metszéspontpár is szerepel; ilyenkor a bizonyítandó állításnak még több példányát fedezhetjük fel az ábrában.
A Vite-formulák egyszerű összefüggéseket biztosítanak egy másodfokú egyenlet gyökei között; a geometriai ábránkban ezeknek a metszéspontpárok közötti geometriai kapcsolatok felelnek meg. Úgy is mondhatjuk, hogy a feladat által leírt alakzat csupán része egy nagyobb ábrának, és a nagyobb ábráról, ahol a másik metszéspontot is felvesszük, több geometriai összefüggést olvashatunk le. Természetesen a nagyobb ábra még nem jelenti azt, hogy a megoldás innen kezdve automatikus, de több esélyünk van meglátni a megoldást, mintha az ábrának csak egy kicsi részletében keresgélnénk.

1. feladat (IMO 2012/5).

Legyen az

A B C

háromszögben

B C A ∢ = 90^{\circ}

, és legyen

D

C

-ből induló magasságvonal talppontja. Legyen

X

C D

szakasz belső pontja. Legyen

K

A X

szakasznak az a pontja, amire

B K = B C

. Hasonlóan, legyen

L

B X

szakasznak az a pontja, amire

A L = A C

. Legyen

M

A L

és

B K

egyenesek metszéspontja. Bizonyítsuk be, hogy

M K = M L

Mit is jelent az a mondat, hogy ,,Legyen

K

A X

szakasznak az a pontja, amire

B K = B C

''? Hogy szerkesztenénk meg a

K

pontot? Egyszerű: az

A X

szakaszt elmetsszük a

B

középpontú,

C

-n átmenő

k_{B}

körrel. Hasonlóan, az

L

pont a

B X

szakasz és az

A

középppontú,

C

-n átmenő

k_{A}

kör metszéspontja.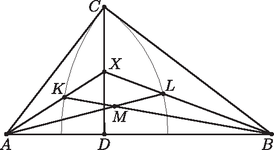

Most keressük elő a tarisznyánkból az otthonról hozott hamuban sült Jótanácsot, és alkalmazzuk. Az

A X

egyenes két pontban metszi a

k_{B}

kört, az egyik a már ismert

K

pont; a másikat jelöljük

K'

-vel. Hasonlóan, a

B X

egyenes kétszer metszi a

k_{A}

kört; az egyik metszéspont az

L

; a másikat jelölje

L'

. Végül, a

k_{A}

és a

k_{B}

kör is kétszer metszi egymást; az egyik metszéspont

C

; a másik a

C

tükörképe az

A B

egyenesre; legyen ez

C'

.
Az

X

pontnak a

k_{B}

és a

k_{A}

körre vonatkozó hatványa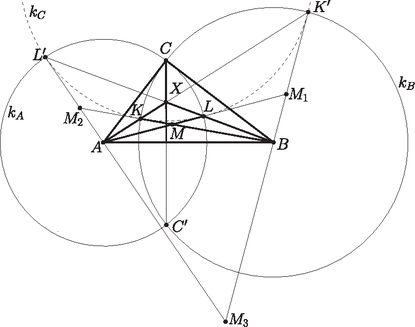

\begin{matrix} X K \cdot X K' = X C \cdot X C' = X L \cdot X L', \end{matrix}

ebből pedig láthatjuk, hogy a

K, K', L, L'

pontok egy körön vannak; jelöljük ezt a kört

k_{C}

-vel.

A megoldás kulcsa az az észrevétel, hogy az

A L

és

B K

szakasz érinti a

k_{C}

kört. Az

A

pont a

k_{B}

és

k_{C}

körök hatványvonalán, az

K K'

egyenesen van, tehát az

A

pontnak a

k_{B}

és

k_{C}

körre vonatkozó hatványa ugyakkora; az

A

pontból ugyanolyan hosszú érintőket húzhatunk a két körhöz. Az egyik ilyen érintő az

A C

szakasz, amely merőleges a

k_{B}

kör

B C

sugarára. Ezért az összesen négy érintési pontot a

k_{A}

kör metszi ki a

k_{B}

és

k_{C}

körökből; ez a négy pont a

k_{B}

körön

C

és

C'

, a

k_{C}

körön pedig

L

és

L'

. Az

A L

és

A L'

szakaszok tehát érintik

k_{C}

-t. Hasonlóan láthatjuk, hogy a

B K

és a

B K'

szakasz is érinti

k_{C}

-t.
Végül, az

M K

és

M L

szakaszok éppen az

M

pontból a

k_{C}

körhöz húzott érintő szakaszok, tehát egyforma hosszúak.
Ha maradéktalanul végre akarjuk hajtani a Jótanácsot, akkor megrajzoljuk az

A L'

és

B K'

egyenesek további metszéspontjait is; az ábrán ezeket jelöli

M_{1}

M_{2}

és

M_{3}

. A bizonyítandó állításnak összesen négy példányát találhatjuk meg az ábrában:

\begin{matrix} M K = M L, M_{1} K' = M_{1} L, M_{2} K = M_{2} L' és M_{3} K' = M_{3} L' . \end{matrix}

2. feladat (IMO 2015/3).¹

Legyen

A B C

egy hegyesszögű háromszög, amiben

A B > A C

. Legyen

Γ

ezen háromszög körülírt köre,

H

a magasságpontja és

F

A

-ból kiinduló magasság talppontja. Legyen

M

B C

szakasz felezőpontja. Legyen

Q

Γ

-nak az a pontja, amire

H Q A ∢ = 90^{\circ}

, és

K

Γ

-nak az a pontja, amire

H K Q ∢ = 90^{\circ}

. Feltesszük, hogy az

A

B

C

K

Q

pontok mind különbözőek, és ilyen sorrendben követik egymást a

Γ

körön.
Bizonyítsuk be, hogy a

K Q H

és

F K M

háromszögek körülírt körei érintik egymást.

A megoldás első lépése egy egyszerű észrevétel: a

Q

pont az

M H

félegyenesen van. Jól ismert, hogy egy háromszög magasságpontjának az oldalegyenesekre, illetve az oldalak felezőpontjaira vonatkozó tükörképei a körülírt körön vannak, utóbbiak a körülírt körön a csúcsokkal átellenes pontok. Legyen

H

tükörképe a

B C

egyenesre

K'

, az

M

pontra

Q'

. (Hogy miért ilyen furcsán jelöljük ezt a két pontot, rövidesen kiderül.) Ekkor tehát

A Q'

a körnek átmérője. Mivel

A Q H ∢

derékszög, a Thalész-tétel megfordítása miatt a

Q H

egyenes átmegy a kör

A

-val átellenes pontján,

Q'

-n. Tehát a

H Q

egyenes tartalmazza a

H Q'

szakaszt és annak felezőpontját,

M

-et. Ebből láthatjuk, hogy a

Q

H

M

Q'

pontok, ebben a sorrendben, egy egyenesen vannak.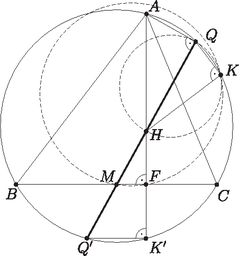

Innentől kezdve már nem lesz szükségünk az

A

pontra.
Most alkalmazzuk a Jótanácsot. A

Q

pont a körülírt kör és az

M H

egyenes egyik metszéspontja; a másik metszéspont

Q'

. Mi történne, ha a

Q

pont helyett a

Q'

ponttal kellene megoldanunk a feladatot? Először is észrevehetjük, hogy a

K

pont helyett a

K'

pontot kell használnunk: ez az a pont a körön, amire

Q' K' H ∢ = 90^{\circ}

. Mivel

Q' K' H ∢ = 90^{\circ}

, a

K' Q' H

kör középpontja az

M

pont; az

M K'

szakasz ennek a körnek egy sugara. Hasonlóan, mivel

K' F M ∢ = 90^{\circ}

, az

F K' M

körnek

K' M

egy átmérője. Így a

K' Q' H

és az

F K' M

kör középpontja is az

M K'

egyenesre esik, a két kör a

K'

pontban érinti egymást. Ha tehát a feladatban a

Q

pontot kicseréljük a

Q'

pontra, egy könnyen ellenőrizhető állítást kapunk.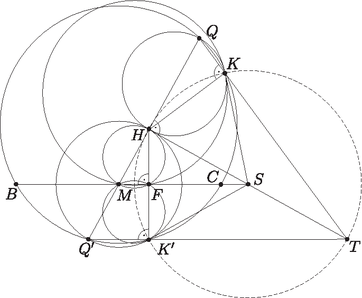

Tekintsük most a háromszög körülírt körét, a

H Q K

kört és

H Q' K'

kört, valamint ezek páronként vett hatványvonalait. A

H Q K

körben

H Q

, a

H Q' K'

körben

H Q'

átmérő és

Q

H

Q'

egy egyenesen vannak. Ezért a

H Q K

és a

H Q' K'

körök érintik egymást. Tehát a három kör páronként vett hatványvonalai a metszéspontokat összekötő

Q K

, illetve a

Q' K'

egyenesek, valamint a

H Q K

és

H Q' K'

körök belső közös érintője, az

M H

egyenesre

H

-ban állított merőleges. Ezek egy ponton, a három kör hatványpontján mennek át; jelöljük ezt

T

-vel. A

K

-nál és

K'

-nél levő derékszögek miatt

H K' T K

húrnégyszög, a köré írt körben

H T

átmérő. Legyen most

S

H K' T K

kör középpontja, ami nem más, mint a

H T

szakasz felezőpontja; ekkor tehát

S H = S K = S K' = S T

. A

H K'

húr felező merőlegese, a

B M F C

egyenes is átmegy

S

-en, a kör középpontján.
Az

S H

szakasz érinti a

H K Q

és a

H K' Q'

kört is. Mivel pedig

S H = S K = S K'

, az

S K

szakasz a

K

pontban érinti a

H K Q

kört, az

S K'

szakasz pedig

K'

-ben érinti a

H K' Q'

kört. Az

S

pontnak a

H M F

körre vonatkozó hatványa

S M \cdot S F = S H^{2} = S K^{2}

; ebből következik, hogy az

F K M

kör a

K

pontban érinti az

S K

szakaszt. Az

S K

szakaszt tehát az

F K M

kör és a

H K Q

kör is érinti a

K

pontban; a két kör tehát egymást is érinti.

¹Az idei olimpiai feladatok megoldását a 386‐395. oldalakon közöljük.