|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A hagyományoknak megfelelően ebben az évben is közöljük a nyári matematikai diákolimpia feladatainak a megoldásait; lényegében úgy, ahogyan a legilletékesebbek, a magyar csapat tagjai leírták. Közreműködésüket köszönjük és ezúton is gratulálunk eredményeikhez.
1. A sík pontjainak egy véges halmazát kiegyensúlyozottnak nevezzük, ha bármely két különböző , pontjához van -nek olyan pontja, amire . -et centrum-nélkülinek nevezzük, ha bármely három páronként különböző , , pontjára teljesül az, hogy nincs -nek olyan pontja, amire .
Mutassuk meg, hogy bármely egész számhoz létezik elemű kiegyensúlyozott halmaz.
Határozzuk meg azokat az egészeket, amelyekre létezik elemű kiegyensúlyozott, centrum-nélküli halmaz.
Di Giovanni Márk megoldása. Ha páratlan, akkor tekintsünk egy szabályos -szöget és lássuk be, hogy ez egy kiegyensúlyozott halmaz. Ehhez tekintsünk két tetszőleges, különböző és pontot és a távolságukat ívhosszban mérve (a sokszög körülírt köre mentén). Ekkor a két távolság (a hosszabb és rövidebb ív mentén) összege , azaz páratlan, ezért az egyik távolság páratlan a másik pedig páros. Ha viszont az egyik ív hossza páros, akkor tartalmazza az ívfelezőpontot, ami ugyanakkora távolságra van -tól és -től.
Ha páros, akkor tekintsünk egy kört és legyen a következő pontok halmaza: a kör középpontja és a kör kerületének néhány pontja az ábra szerint: , , úgy, hogy rombusz legyen, továbbá tetszőleges darab pont , illetve ezen pontok körüli -os pozitív iránybeli elforgatottja .
Nyilván megválaszthatjuk a -pontokat úgy, hogy az összes általunk kiválasztott pont különböző legyen. Ekkor -nek pontosan darab eleme van (ahol tetszőleges nemnegatív egész). Tekintsünk most két különböző -beli pontot. Ha mindkettő a kör kerületén van, akkor a kör középpontja egyenlő távol van tőlük. Ha az egyik a kör középpontja, akkor mivel -nek, -nek, illetve -nek a -os elforgatottja, ezért a szabályos háromszögek miatt azonnal találunk olyan pontot, ami a két kiválasztott ponttól egyenlő távolságra van. Ezzel beláttuk, hogy kiegyensúlyozott. Továbbá felveszi az összes 3-nál nagyobb páros számot.
Tehát minden egészre létezik elemű kiegyensúlyozott halmaz.
Azt állítjuk, hogy pontosan a páratlan -ekre létezik elemű kiegyensúlyozott, centrum-nélküli halmaz.
Ha páratlan, akkor a szabályos -szög kiegyensúlyozott halmaz (ezt már korábban beláttuk), továbbá bármely három pontját is választjuk ki, az a pont, amely mindhármuktól egyenlő távolságra van, éppen a körülírt körük középpontja, ami nyilván megegyezik a szabályos -szög körülírt körének középpontjával. Ez a pont viszont nem -beli, tehát centrum-nélküli.
Lássuk most be, hogy páros -re nem létezik ilyen halmaz. Legyen és tegyük fel indirekt, hogy találtunk ilyen -et. Ekkor egy tetszőleges csúcshoz legfeljebb darab -beli pontpár található úgy, hogy rajta legyen a felezőmerőlegesükön, mert ha létezne ilyen pár, akkor a csúcs közül lenne olyan pont, amihez tartozó két felezőmerőlegesen is rajta lenne az pont. Tekintsük ezen felezőmerőlegeseket meghatározó szakaszokat: -t és -t. Ekkor és -ből következik, tehát -nek van centruma, ami ellentmond eredeti feltevésünknek. Tehát -nek minden csúcsa legfeljebb darab különböző -beli pontpár által meghatározott felezőmerőlegesen lehet rajta. Viszont összesen darab pontpár van, amelyek mindegyikéhez tartozik egy felezőmerőleges, továbbá minden pontpár által meghatározott felezőmerőlegesen van legalább egy darab -beli pont.
Tehát , azaz , ami nyilvánvalóan ellentmondás. Így páros -re nincsen kiegyensúlyozott, centrum-nélküli halmaz.
Összefoglalva: pontosan a páratlan -ekre létezik kiegyensúlyozott, centrum-nélküli halmaz.
2. Határozzuk meg azokat a pozitív egész számokból álló számhármasokat, amelyekre az számok mindegyike -hatvány.
(-hatvány egy alakú egész szám, ahol egy nemnegatív egész szám.)
Szabó Barnabás megoldása. A szokásos módon jelöli egy pozitív egész prímfelbontásában a 2 hatványkitevőjét. A továbbiakban hivatkozás nélkül fel fogjuk használni azt az ismert állítást, mely szerint esetén , és esetén . Ha , akkor és közül az egyik nem pozitív, így nem lehet 2-hatvány. Tehát , hasonlóan .
1. eset: minden változó páros. A szimmetria miatt feltehetjük, hogy . Ekkor , de 2-hatvány, így , azaz . A egyenlőségből kapjuk, hogy . A két egyenlőtlenséget összeszorozva nyerjük, hogy , de , így . Ezt visszahelyettesítve kapjuk, hogy és , azaz , viszont ekkor , tehát lesz, ahonnan . Az első eset tehát az számhármast adja, ami valóban megfelelő.
2. eset: egyik változó páratlan. Feltehető, hogy lesz páratlan. Tegyük fel, hogy , mondjuk . Ekkor páros, tehát páratlan, azaz . Másrészt, , így osztója -nek, . Ekkor , ahonnan , így és , ami ellentmond -nek.
Tehát . Először tegyük fel, hogy . Ekkor , így . A -t behelyettesítve
ahol feltehető, hogy . A kettőt kivonva, adódik. Hogyha , akkor lesz, és . Mivel páros, , így , adódik. Ebből kapjuk a számhármast.
Ha , akkor miatt , de , így . Ebből , de miatt . Másrészt miatt , azaz . Legyen és , ekkor az egyenletbe helyettesítve és -vel osztva , tehát , ezért . Ebből miatt , ahonnan . Ha , akkor , innen (hiszen ), innen ismét kapjuk a számhármast. Hasonló vizsgálattal adódik, hogy esetén nincs megoldás, míg esetén kapjuk a hármast.
Most azt az esetet vizsgáljuk, amikor , azaz mindhárom szám páratlan. Legyen , , . Feltehető, hogy . Ekkor és . Nyilván vagy , innen . Viszont , de , tehát . esetén lenne, ami ellentmondás. Tehát csak lehetséges. Mivel , így tehát vagy . Az előbbi esetből egyszerű számolás után ellentmondásra jutunk, míg az utóbbiból a megoldást kapjuk, ami valóban jó. A megoldások tehát: , , és és persze ezek permutációi.
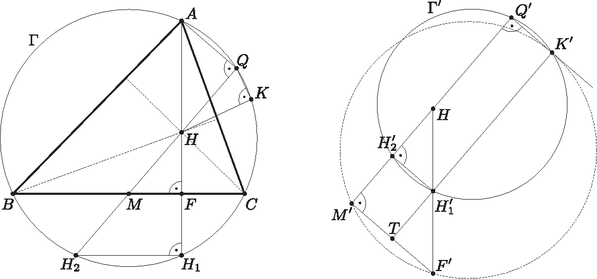
3. Legyen egy hegyesszögű háromszög, amiben . Legyen ezen háromszög körülírt köre, a magasságpontja és az -ból kiinduló magasság talppontja. Legyen a szakasz felezőpontja. Legyen -nak az a pontja, amire , és -nak az a pontja, amire . Feltesszük, hogy az , , , , pontok mind különbözőek, és ilyen sorrendben követik egymást a körön.
Bizonyítsuk be, hogy a és háromszögek körülírt körei érintik egymást.
Janzer Barnabás megoldása. Legyen a pont tükörképe a egyenesre (vagyis az pontra) , az pontra . Ismert, hogy és a körön vannak, továbbá az -val átellenes pont. A Thalész-tétel megfordításából a egyenes -t az -val átellenes pontban, vagyis -ben metszi. Ezért és is átmegy -n, vagyis , , és egy egyenesen vannak. Az , és pontok egy egyenesen vannak, ezért a Thalész-tételből . Az , , pontokra a továbbiakban nincs szükségünk a megoldás során.
Invertáljunk középponttal. Ekkor , , , ilyen sorrendben egy egyenesen vannak. Thalész-köre (melyen rajta van) egy -re merőleges egyenesbe megy át (hiszen középpontja rajta van a egyenesen). Hasonlóan és Thalész-körének képe is egy -re merőleges egyenes, előbbi körön , utóbbin rajta van. Továbbá és rendre a és szakasz felezőpontja. egy kör, mely áthalad a , , , pontokon.
négyszög derékszögű trapéz és húrnégyszög egyben, ezért téglalap. Messe egyenes -t a pontban. -ban középvonal, mivel felezőpont és párhuzamos -vel. Ezért egyenes szakaszfelező merőlegese az szakasznak, így a szimmetria miatt körülírt köre érinti (az -vel párhuzamos) egyenest. Így ősképeik is érintik egymást, ami pont a bizonyítandó állítás.
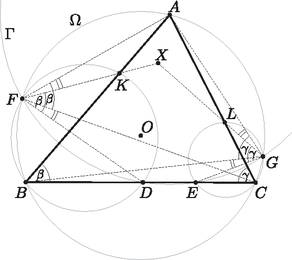
4. Az háromszög körülírt köre , a körülírt kör középpontja . Egy középpontú kör a szakaszt a és pontokban metszi, ahol , , , páronként különböző pontok, amelyek a egyenesen ebben a sorrendben fekszenek. Legyenek és a és körök metszéspontjai, ahol , , , , ebben a sorrendben követik egymást az körön. Legyen a háromszög körülírt körének és az szakasznak a másik metszéspontja. Legyen a háromszög körülírt körének és a szakasznak a másik metszéspontja.
Tegyük fel, hogy az és egyenesek különbözők és az pontban metszik egymást. Bizonyítsuk be, hogy az pont az egyenesen fekszik.
Baran Zsuzsanna megoldása. Először belátom, hogy .
, mert körnek azonos ívén nyugvó kerületi szögek.
Az háromszögben .
Mivel húrnégyszög, az is igaz, hogy .
Ezek szerint .
A kerületi szögek tétele miatt az is igaz, hogy
Ezek szerint AFX∢=AFK∢=AGL∢=AGX∢.
Az AFG háromszög egyenlőszárú (AF és AG egyaránt Γ sugarai), ezért AFG∢=AGF∢ és A illeszkedik az FG szakasz felezőmerőlegesére.
OF=OG (Ω sugarai), ezért O is illeszkedik az FG szakasz felezőmerőlegesére. Így az AO egyenes az FG szakasz felezőmerőlegese. | XFG∢=|AFG∢-AFX∢|=|AGF∢-AGX∢|=XGF∢. |
Ezek szerint az XFG háromszög egyenlőszárú, így az X pont illeszkedik az FG szakasz felezőmerőlegesére, azaz az AO egyenesre. Ezt akartuk belátni.
Mivel a feladatban megadták, hogy a pontok milyen sorrendben helyezkednek el a BC szakaszon, illetve az Ω körön, diszkusszióra nincs szükség.
5. Jelölje R a valós számok halmazát. Határozzuk meg az összes olyan f:R→R függvényt, amelyre teljesül | f(x+f(x+y))+f(xy)=x+f(x+y)+yf(x) | (1) |
minden x, y valós számra.
Williams Kada megoldása. Mindenekelőtt keressük meg (1) lineáris megoldásait, vagyis az f(x)=ax+b alakúakat! Beírva (1)-be, majd kibontva és átrendezve:
a(x+a(x+y)+b)+b+axy+b=x+a(x+y)+b+y(ax+b),(a2-1)x+(a2-a-b)y+(ab+b)=0.(*)
Meggondolható, hogy ez éppen akkor állhat fenn minden x, y-ra, hogyha (*)-ban mindhárom együttható nulla, ami csak akkor lehet igaz, ha (a,b)=(1,0) vagy (-1,2), azaz f(x)=x vagy f(x)=2-x. Ennek a meggondolása nem tartozik a megoldáshoz, viszont ebből sejthető meg, hogy ez a kettő lesz (1)-nek az összes megoldása. Jól látható, hogy ezeknél (*) együtthatói tényleg mind nullák lesznek, vagyis hogy f(x)=x és f(x)=2-x valóban megoldása (1)-nek.
Helyettesítsünk x=0-t, majd pedig y=1-et (1)-be, nyerjük:
f(f(y))+f(0)=f(y)+yf(0),(2)f(x+f(x+1))=x+f(x+1).(3)
Kezdésképpen könnyű megtalálni f(0) lehetséges értékeit: írjunk (2)-be előbb y=0-t: f(f(0))=0 adódik, amiért (2)-be most y=f(0)-t helyettesítve | f(f(f(0)))+f(0)=f(f(0))+f(0)2, |
azaz 2f(0)=f(0)2 adódik, ahonnan f(0)=2 vagy f(0)=0.
1. eset: f(0)=2, itt az f(x)=2-x megoldást várjuk.
Ez az eset egy trükkös észrevétellel elintézhető. Figyeljük meg ugyanis, hogy (3) szerint x+f(x+1) minden x-re fixpontja f-nek. Ellenben a megcélzott x↦2-x függvénynek csak az 1 a fixpontja. Ha belátnánk, hogy f(0)=2 esetén f-nek csak az 1 lehet fixpontja, abból következne, hogy x+f(x+1) fixpont lévén minden x-re, azonosan 1 kell legyen, vagyis f(x+1)=1-x minden x-re, azaz f(t)=2-t bármely t-re (t:=x+1).
Belátjuk tehát, hogy f(0)=2-re f(a)=a-ból a=1 következik. Ehhez (2)-t vegyük szemügyre, y=a-t helyettesítve: f(f(a))+2=f(a)+2a, a=1 adódik. Ez igazolja, hogy f(0)=2 esetén f(x)=2-x.
2. eset: f(0)=0, itt az f(x)=x megoldást várjuk.
Ezúttal bonyolultabban járunk el: azt vesszük észre, hogy ha (1)-be x, y helyett -x, -y-t helyettesítünk, azzal f(xy) ugyanúgy jelen marad, és ezért kiejthetjük:
f(xy)=-f(x+f(x+y))+(x+f(x+y))+yf(x)f(xy)=-f(-x+f(-x-y))+(-x+f(-x-y))-yf(-x).
Itt gyakran üti fel fejét x+y és ellentettje, kényelmesebb az y:=k-x jelölést használni:
-f(x+f(k))+(x+f(k))+(k-x)f(x)=(4)=-f(-x+f(-k))+(-x+f(-k))-(k-x)f(-x).
A megoldáshoz először meghatározunk néhány f(±k) értéket, majd pedig az adódó összefüggéseket összehasonlítjuk, amikből már némi munka árán kifejezhetjük f(x)-et.
Már tudjuk, hogy f(0)=0, írjunk hát (4)-be k=0-t, rögtön barátságosabb lesz:
-f(x)+x-xf(x)=-f(-x)-x+xf(-x),2x=(x+1)f(x)+(x-1)f(-x).(5)
Ha (3)-ba x=-1-et írunk, akkor f(0)=0 miatt f(-1)=-1 nyerhető, illetve (5)-be x=1-et írva, megkapjuk, hogy 2=2f(1), f(1)=1. Vagyis (4)-be már írhatunk k=1-et is: | -f(x+1)+(x+1)+(1-x)f(x)=-f(-x-1)-(x+1)-(1-x)f(-x). |
Itt viszont (5) szerint -(1-x)f(-x) helyére 2x-(x+1)f(x) írható, vagyis
-f(x+1)+2(x+1)=(x-1)f(x)-f(-x-1)+2x-(x+1)f(x),2+2f(x)=f(x+1)-f(-x-1).
Ha ezt x helyett x-1-re írjuk fel, akkor adódik.
Beszorozva (6)-ot (x-1)-gyel, majd hozzáadva (5)-öt:
2(x-1)+2(x-1)f(x-1)+2x=(x-1)f(x)+(x+1)f(x),(x-1)f(x-1)+(2x-1)=xf(x).(7)
Ezután (6)-ba x=-1-et írva, f(-2)=-2, majd pedig (6)-ba x=2-t írva, f(2)=2 nyerhető.
A befejezéshez írjunk (4)-be k=2-t: | -f(x+2)+(x+2)+(2-x)f(x)=-f(-x-2)+(-x-2)-(2-x)f(-x), |
ahol f(x+2)-f(-x-2)=2+2f(x+1) érvényes (6) szerint, így | 2(x+2)+(2-x)⋅(f(x)+f(-x))=2+2f(x+1). |
Beszorozva (x+1)-gyel, (7) miatt adódik:
2(x+2)(x+1)-(x-2)(x+1)⋅(f(x)+f(-x))=2(x+1)+2(xf(x)+2x+1),2(x2+3x+2)-2(x+1)-2(2x+1)=(x2-x-2)(f(x)+f(-x))+2xf(x),2x2=(x2+x-2)f(x)+(x2-x-2)f(-x).
Ezt pedig (x-1)-gyel tovább szorozva és (5)-öt használva:
2x2(x-1)=(x-1)(x2+x-2)f(x)+(x2-x-2)(2x-(x+1)f(x)),2x2(x-1)-2x(x2-x-2)=[(x-1)(x2+x-2)-(x+1)(x2-x-2)]f(x),2x(x2-x-(x2-x-2))==[x((x2+x-2)-(x2-x-2))-((x2+x-2)+(x2-x-2))]f(x),4x=[x⋅(2x)-(2x2-4)]f(x),
amiből már világos, hogy f(x)=x, bármely x-re.
Tehát két megoldásunk van: f(x)=x és f(x)=2-x, és ezeket már leellenőriztük.
6. Egész számok egy a1,a2,... sorozata rendelkezik az alábbi két tulajdonsággal:
(i) 1≤aj≤2015 minden j≥1-re;
(ii) k+ak≠ℓ+aℓ minden 1≤k<ℓ-re.
Bizonyítsuk be, hogy van két olyan pozitív egész: b és N, hogy teljesül minden olyan m és n egész számra, amire fennáll n>m≥N.
Fehér Zsombor megoldása. Legyen cj=aj+j. Ekkor az (i) feltétel azt mondja ki, hogy j+1≤cj≤j+2015, a (ii) feltétel pedig azt, hogy a cj számok mind különbözőek.
Megmutatjuk, hogy a c1,c2,... sorozat véges sok kivétellel minden pozitív egész számot felvesz. Tegyük fel ugyanis, hogy legalább 2016-ot nem vesz fel, és legyen t egy olyan pozitív egész, ami nagyobb ennél a 2016 számnál. Ekkor az (i) feltétel alapján a {c1,c2,...,ct} halmaz minden eleme az [1,t+2015] intervallumba esik, és mivel (ii) szerint t különböző elemről van szó, ezért ebből az intervallumból {c1,c2,...,ct} éppen 2015 pozitív egész számot nem vesz fel. Azonban feltevésünk szerint az ennél bővebb {c1,c2,...} halmaz legalább 2016 darab t-nél kisebb pozitív egész számot nem vesz fel, ami pedig ellentmondás.
A feladatnak megfelelő b számot válasszuk meg annyinak, amennyi a c1,c2,... sorozat által fel nem vett pozitív egészek száma, N pedig legyen egy olyan szám, ami nagyobb ennél a b darab kimaradó számnál. A fenti gondolatmenetből az is látható, hogy b≤2015. Az m, n pozitív egészekre a továbbiakban feltesszük, hogy N≤m<n.
A feladatunk lényegében az, hogy egy ∑aj kifejezést megfelelő korlátok közé szorítsunk, ami nyilván ugyanaz, mint ∑cj megfelelő korlátok közé szorítása. Tudjuk, hogy {cm+1,...,cn} minden eleme az [m+2,n+2015] intervallumba esik, és mivel ezen intervallum n-m+2014 egész számából n-m van az előző halmazban, ezért 2014 egész szám marad ki. Vizsgáljuk meg közelebbről ezt a 2014 számot: ki fog derülni, hogy közülük b-1 darab az [m+2,n+2015] intervallum ,,elején'', 2015-b pedig a ,,végén'' helyezkedik el.
Mivel a {c1,c2,...} halmaz b darab egész számot nem vesz fel az [1,∞) intervallumból, ezért a {cm+1,cm+2,...} halmaz b+m számot nem vesz fel [1,∞)-ből. Ez cj>j alapján azt jelenti, hogy a {cm+1,cm+2,...} halmaz b-1 számot nem vesz fel [m+2,∞)-ből. Mivel azonban m+2>N, ezért ezen b-1 számot is felveszi valahol a c1,c2,... sorozat, csak még cm+1 előtt. Így ez a b-1 szám mindegyike olyan ck, melyre k≤m, így ck≤k+2015≤m+2015 alapján ezek a számok mind az [m+2,m+2015] intervallumba esnek.
Tehát azon 2014 egész közül, melyek az [m+2,n+2015] intervallumban benne vannak, de a {cm+1,...,cn} halmazban nem, b-1 darab az {c1,...,cm} halmazban van, a maradék 2015-b darab pedig szükségképpen a {cn+1,...} halmazban. Ezen 2015-b szám mindegyike legalább n+2, így ezek az [n+2,n+2015] intervallumba esnek.
Ezen a ponton álljunk meg egy pillanatra, és vegyük észre, hogy a feladat megoldásával lényegében készen vagyunk. Csak az alapján, hogy a 2014 kimaradó szám valahol az [m+2,n+2015] intervallumban van, még nem tudnánk pontos becslést mondani, hiszen m,n-et kicsivel megváltoztatva az egyik kimaradó szám szabadon ,,átugorhatna'' az intervallum elejéről a végére, ezzel nagy (n-m nagyságrendű) változást eredményezve. De azáltal, hogy a 2014 kimaradó szám közül mindig b-1 van az intervallum elején, és 2015-b a végén (ahol a b egy univerzális paramétere a sorozatnak!), ilyen ugrások nem történhetnek meg, csak az intervallum szélein lévő rövid (2014 hosszú) intervallumok belsejében mozoghatnak a kimaradó számok. Így lehetséges az, hogy m, n-től független, 10072 nagyságrendű becslést fogunk tudni mondani.
Nem maradt más hátra, minthogy kiszámoljuk a 2014 kimaradó szám összegének lehetséges legkisebb és legnagyobb értékét, majd ezt visszavezessük a feladatbeli összegre. Tudjuk, hogy a 2014 szám felbontható valahogy egy b-1 és egy 2015-b elemű csoportra, melyek elemei rendre az [m+2,m+2015], illetve az [n+2,n+2015] intervallumból valók. (Előfordulhat, hogy ez a két intervallum átfedi egymást, de ez nem okoz gondot.) Mivel a számok különbözőek, ezért a 2014 szám összege legalább
((m+2)+(m+3)+⋯+(m+b))++((n+2)+(n+3)+⋯+(n+2016-b))==(b-1)(2m+b+2)2+(2015-b)(2n+2018-b)2=hmin,
legfeljebb pedig
((m+2017-b)+⋯+(m+2015))+((n+b+1)+⋯+(n+2015))==(b-1)(2m+4032-b)2+(2015-b)(2n+2016+b)2=hmax.
Ha H jelöli az előbbi 2014 kimaradó szám összegét, akkor a feladatban szereplő összeg így írható:
∑j=m+1n(aj-b)=∑j=m+1n(cj-j-b)=∑i=m+2n+2015i-H-∑j=m+1nj-∑j=m+1nb==(n+2014-m)(n+m+2017)2-H-(n-m)(n+m+1)2-b(n-m).
A hmin≤H≤hmax becslést alkalmazva, a kifejezések egyszerűsítése után végül a következőt kapjuk: | b2-2016b+2015≤∑j=m+1n(aj-b)≤-b2+2016b-2015. |
Így tehát valóban, | |∑j=m+1n(aj-b)|≤-b2+2016b-2015=10072-(b-1008)2≤10072. |
|
 PDF | MathML
PDF | MathML