Kezdőlap


Cím:	A Kunfalvi Rezső Olimpiai Válogatóverseny elméleti feladatainak megoldása
Füzet:	2015/október, 433 - 441. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

¹
1. feladat.

1.A. Ez a részfeladat megegyezik a jelen számunkban kitűzött P. 4767. feladattal, emiatt a megoldását később közöljük (‐ a szerk.).

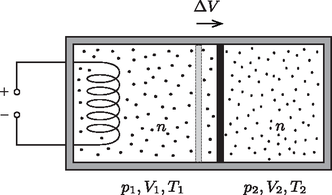
1.B. Jelöljük a gázok kezdeti állapotjelzőit

p_{0}

-lal,

V_{0}

-lal és

T_{0}

-lal, mólszámukat pedig

n

-nel (ezek a bal és a jobb oldali rekeszre ugyanakkorák), egy kicsiny hő közlése után kialakuló állapotot pedig jellemezzük az 1. ábrán látható mennyiségekkel.

1. ábra

A dugattyú egyensúlya miatt

p_{1} = p_{2}

, az össztérfogat állandósága miatt pedig

\begin{matrix} V_{1} = V_{0} + Δ V, V_{2} = V_{0} - Δ V \end{matrix}

írható. A jobb oldali rekeszben lévő gáz nem vett fel hőt, állapotváltozása adiabatikus, így fennáll

\begin{matrix} p_{0} V_{0}^{κ} = p_{2} {(V_{0} - Δ V)}^{κ}, (héliumra κ = \frac{f + 2}{f} = \frac{5}{3}), \end{matrix}

ebből (

Δ V ≪ V_{0}

esetén)

\begin{matrix} p_{2} = p_{0} {(\frac{1}{1 - \frac{Δ V}{V_{0}}})}^{κ} \approx p_{0} (1 + κ \frac{Δ V}{V_{0}}) \end{matrix}

(1)

következik. A bal oldali rekeszben lévő gázra a hőtan I. főtétele szerint

\begin{matrix} C n Δ T = \frac{f}{2} n R Δ T + p_{2} Δ V, \end{matrix}

ahol

C

a mólhőt jelöli. Az (1) összefüggés felhasználásával és a

{(Δ V)}^{2}

-tel arányos (másodrendűen kicsiny) tagokat elhagyva

\begin{matrix} C = \frac{f}{2} R + p_{0} \frac{Δ V}{n Δ T} \end{matrix}

(2)

adódik. Az ideális gázok állapotegyenletéből

\begin{matrix} n R Δ T = p_{0} Δ V + V_{0} Δ p, \end{matrix}

ahonnan (1)-et felhasználva

\begin{matrix} n R Δ T = (1 + κ) p_{0} Δ V, \end{matrix}

tehát

\begin{matrix} \frac{Δ V}{n Δ T} = \frac{R}{p_{0}} \frac{1}{1 + κ} \end{matrix}

következik. Ezt (2)-be helyettesítve (tudván, hogy héliumra

f = 3

) megkapjuk a keresett mólhőt:

\begin{matrix} C = \frac{f}{2} R + \frac{1}{1 + κ} R = \frac{f^{2} + 2 f}{2 (f + 1)} R = \frac{15}{8} R . \end{matrix}

1.C. A cél a voltmérő által jelzett

U

feszültség és a lemezbe vezetett

I

áramerősség közötti összefüggés megállapítása. Ha ismernénk a kialakuló kétdimenziós árameloszlás (helyfüggő)

j (r)

áramsűrűségét, akkor az

E (r) = ϱ j (r)

differenciális Ohm-törvényből meghatározhatnánk az elektromos térerősséget a lemez belsejében. A térerősségből a

C

és

D

pontok közötti feszültséget integrálással már ki tudnánk számítani. Ez matematikailag nehéz feladat, de szerencsére van egy sokkal könnyebb út.
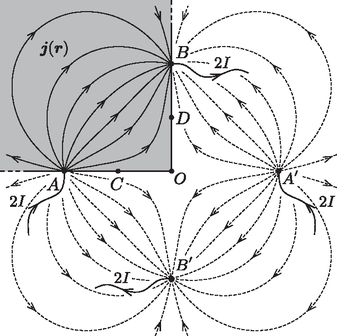
A fémlemez éleinél a

j (r)

áramsűrűség-vektor élre merőleges komponensének el kell tűnnie. Ez a szokatlan határfeltétel könnyen kezelhető, ha az elektrosztatikában használt tükörtöltés-módszerhez hasonló gondolatmenetet követünk (lásd a 2. ábrát). Ehhez tükrözzük az

A

és

B

pontokat a lemez

B D

és

A C

oldaléleire; az így kapott pontokat jelölje

A'

és

B'

. A véges lemezbeli árameloszlás éppen olyan, amilyen egy végtelen kiterjedésű fémlemez egyik negyedében alakulna ki, ha abba az

A

és

A'

pontokban egyaránt

2 I

erősségű áramot vezetnénk be, a

B

és

B'

pontokból pedig

2 I

áramot vezetnénk el.

2. ábra

Ha csak egyetlen elektródán keresztül vezetnénk

2 I

áramot a végtelen fémlemezbe, akkor az áramsűrűség nagysága

\begin{matrix} j (r) = \frac{2 I}{2 π r δ} \end{matrix}

lenne a bevezetési ponttól

r

távolságra. A lemezbeli térerősség ugyanitt

\begin{matrix} E (r) = \frac{ϱ I}{π r δ} \end{matrix}

értékű, a potenciál pedig (egy önkényesen választható,

r_{0}

távolságra lévő ponthoz képest)

\begin{matrix} Φ (r) = - \int_{r_{0}}^{r} E (r) d r = \frac{ϱ I}{π δ} ln \frac{r_{0}}{r} . \end{matrix}

C

pont potenciálját a valódi és a ,,tükörelektródák'' hatásainak szuperpozíciójaként számolhatjuk. Ha a potenciált a négyzet

O

csúcsában választjuk nullának (ez a pont valamennyi áram be- és kivezetési pontjától

r_{0} = 2 d

távol van), a kérdéses potenciál tehát

\begin{matrix} Φ_{C} = \frac{ϱ I}{π δ} (ln \frac{2 d}{d} + ln \frac{2 d}{3 d} - ln \frac{2 d}{\sqrt[]{5} d} - ln \frac{2 d}{\sqrt[]{5} d}), \end{matrix}

egyszerűsítések után:

\begin{matrix} Φ_{C} = \frac{ϱ I}{π δ} ln \frac{5}{3} . \end{matrix}

Hasonlóan számolhatjuk a

D

pont potenciálját is, és könnyen látszik, hogy

Φ_{D} = - Φ_{C}

. A

C

és

D

pontok közötti feszültség tehát

2 Φ_{C}

, ennyit jelez tehát a véges kiterjedésű lemezre kapcsolt voltmérő is:

\begin{matrix} U = \frac{2 ϱ I}{π δ} ln \frac{5}{3} . \end{matrix}

Ebből a lemez

ϱ

fajlagos ellenállása kifejezhető:

\begin{matrix} ϱ = \frac{π δ}{2 ln (5 / 3)} \frac{U}{I} . \end{matrix}

Érdekes, hogy az eredmény nem függ

d

-től (egészen addig, amíg

d

sokkal kisebb a négyzetlap oldaléleinél, és sokkal nagyobb

δ

-nál.)

2. feladat. Furfangos szökőkút

2.1. A ,,bemerülő'' rész térfogata:

\begin{matrix} V = (\frac{2 θ_{{max}_{}^{}}}{2 π} R^{2} π - 2 sin θ_{{max}_{}^{}} R \cdot cos θ_{{max}_{}^{}} R \cdot \frac{1}{2}) L = \frac{R^{2} L}{2} (2 θ_{{max}_{}^{}} - sin 2 θ_{{max}_{}^{}}) . \end{matrix}

A keresett hányados:

\begin{matrix} \frac{F_{fel}}{m g} = \frac{ϱ_{víz} \frac{R^{2} L}{2} (2 θ_{{max}_{}^{}} - sin 2 θ_{{max}_{}^{}}) g}{ϱ R^{2} π L g} = \frac{ϱ_{víz}}{ϱ} \frac{1}{2 π} (2 θ_{{max}_{}^{}} - sin 2 θ_{{max}_{}^{}}) = 0, 010. \end{matrix}

A felhajtóerő tehát a gránithengerre ható nehézségi erőnek mindössze csak

1 %

-a.

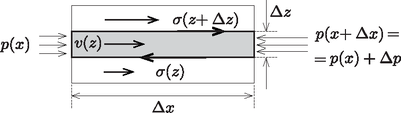
2.2. Tekintsünk három, egymás feletti folyadékréteget (3. ábra). A középső,

Δ z

vastagságú,

ℓ'

szélességű és

Δ x

hosszúságú réteg nem gyorsul, a rá ható erők tehát egyensúlyban vannak:

[σ (z) - σ (z + Δ z)] Δ x ℓ' = [p (x) - p (x + Δ x)] Δ z ℓ'

, ebből valóban

\begin{matrix} \frac{σ (z + Δ z) - σ (z)}{Δ z} = \frac{p (x + Δ x) - p (x)}{Δ x}, vagyis \frac{Δ σ}{Δ z} = \frac{Δ p}{Δ x} \end{matrix}

következik.

3. ábra

2.3. Mivel

\frac{Δ σ}{Δ z} = - K

, így

σ (z) = σ_{0} - K z

. Másrészt a nyírófeszültség definíciója szerint

\begin{matrix} σ (z) = η \frac{d v}{d z}, ezért v (z) = \frac{σ_{0}}{η} z - \frac{K}{2 η} z^{2} + C . \end{matrix}

A folyadék sebessége a határokon (

z = 0

-nál és

z = h

-nál) zérus, tehát

\begin{matrix} v (z) = \frac{K h}{2 η} z - \frac{K}{2 η} z^{2} \equiv \frac{K}{2 η} z (h - z) . \end{matrix}

Ezek szerint a kérdezett együtthatók:

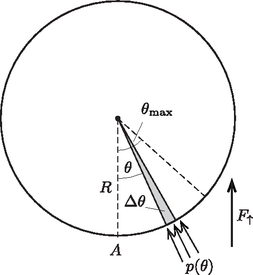
\begin{matrix} A = - \frac{K}{2 η}, B = \frac{K h}{2 η}, C = 0. \end{matrix}

2.4. A nyomás

θ

függvényében a

\frac{Δ p}{Δ x} = - K

feltételből határozható meg (4. ábra):

\begin{matrix} p (θ) = p_{A} - K R θ . \end{matrix}

Mivel

p (θ_{{max}_{}^{}}) = p_{0},

így

p_{A} = p_{0} + K R θ_{{max}_{}^{}},

vagyis

\begin{matrix} p (θ) = p_{0} + K R (θ_{{max}_{}^{}} - θ) . \end{matrix}

A hengerpalást egy kicsiny,

Δ θ

szöggel jellemezhető darabkájára ható nyomásból származó erő függőleges komponense:

\begin{matrix} Δ F_{↑} = L R Δ θ (p (θ) - p_{0}) cos θ, \end{matrix}

hiszen a hengerre mindenhol ható

p_{0}

légnyomás járuléka nyilván kiesik.

4. ábra

Az eredő függőleges irányú erő (a feladatok szövegének végén szereplő matematikai segítség felhasználásával)

\begin{matrix} F_{↑} = 2 R^{2} K L \int_{0}^{θ_{{max}_{}^{}}} (θ - θ_{{max}_{}^{}}) cos θ d θ = 2 R^{2} K L (1 - cos θ_{{max}_{}^{}}) . \end{matrix}

Ennek az erőnek kell egyensúlyt tartania a gránithenger

R^{2} π L ϱ g

súlyával:

\begin{matrix} 2 R^{2} K L (1 - cos θ_{{max}_{}^{}}) = R^{2} π L ϱ g, \end{matrix}

ahonnan megkapjuk az eddig ismeretlen

K

állandót:

\begin{matrix} K = \frac{π ϱ g}{2 (1 - cos θ_{{max}_{}^{}})}, \end{matrix}

valamint a beáramlási pontban a túlnyomást:

\begin{matrix} p_{A} - p_{0} = \frac{π ϱ g R θ_{{max}_{}^{}}}{2 (1 - cos θ_{{max}_{}^{}})} . \end{matrix}

Megjegyzés. A hengerre nemcsak a nyomásból, hanem az áramló folyadékban ébredő nyírófeszültségekből származó erő is hat. A

v (z)

sebességeloszlás ismeretében

σ (z)

is könnyen kiszámítható. Belátható, hogy a nyíróerők járuléka a függőleges irányú erőhöz

h / R

-szer kisebb, mint a nyomásból adódó járulék, tehát az előbbi valóban elhanyagolható.

2.5. A vályú alján található nyíláson beáramló víz ,,hozamát'' az áramlási sebességprofilból tudjuk meghatározni:

\begin{matrix} Q_{be} = 2 \int_{0}^{h} v (z) L d z = 2 \int_{0}^{h} \frac{K}{2 η} z (h - z) L d z = \frac{K L h^{3}}{6 η} = \frac{π ϱ g L h^{3}}{12 η (1 - cos θ_{{max}_{}^{}})} . \end{matrix}

2.6. A

v (0, ω) = 0

és

v (h, ω) = R ω

határfeltételekből következik, hogy

D = R ω / h

, vagyis az áramlási sebességprofil:

\begin{matrix} v (z, ω) = \frac{K h}{2 η} z - \frac{K}{2 η} z^{2} \pm \frac{R ω}{h} z . \end{matrix}

2.7. Amíg a henger nem forog, a jobb és a bal oldalhoz tartozó nyírófeszültségek forgatónyomatéka kiegyenlíti egymást. A forgáskor ez az egyensúly felborul. A sebességprofilnak csak az új,

\pm \frac{R ω}{h} z

tagjából származó járulékot kell vizsgálnunk. A nyírófeszültségekben ennek megfelelő járulék:

\begin{matrix} σ' (z) = η \frac{d}{d z} (\frac{R ω}{h} z) = η \frac{R ω}{h} . \end{matrix}

Ez a (helytől független, de a szögsebességgel arányos) nyírófeszültség mindkét oldalon fékezi a forgást, a forgatónyomatéka

\begin{matrix} M = σ' (z) \cdot L R \cdot 2 θ_{{max}_{}^{}} \cdot R = \frac{2 η L R^{3} θ_{{max}_{}^{}}}{h} ω . \end{matrix}

m = R^{2} π L ϱ

tömegű,

Θ = \frac{1}{2} m R^{2}

tehetetlenségi nyomatékú henger forgásegyenlete:

\begin{matrix} - M = Θ \frac{d ω}{d t}, \end{matrix}

ami a fentebb kiszámított mennyiségek behelyettesítése után így írható:

\begin{matrix} \frac{d ω (t)}{d t} = - \frac{4 η θ_{{max}_{}^{}}}{ϱ π h R} ω (t) \equiv - λ ω (t) . \end{matrix}

Ez a (differenciál)egyenlet a radioaktív bomlások egyenletével analóg, így a megoldása a bomlástörvény ismert alakja:

\begin{matrix} ω (t) = ω_{0} e^{- λ t} \equiv ω_{0} e^{- \frac{4 η θ_{{max}_{}^{}}}{ϱ π h R} t} . \end{matrix}

3. feladat: Fehér törpék keletkezése

3.1. A csillag tömegsűrűsége

\begin{matrix} ϱ = \frac{M}{\frac{4 π}{3} R^{3}} . \end{matrix}

,,Rakjuk össze'' (gondolatban) a csillagot vékony gömbhéjakból (5. ábra)! Amikor a csillag éppen

r

sugarú, a következő,

Δ r

vastagságú gömbhéj darabkáinak a ,,végtelenből'' történő ideszállításakor

\begin{matrix} Δ W = - γ \frac{ϱ \frac{4 π r^{3}}{3} r^{3}}{r} \cdot ϱ 4 π r^{2} Δ r \end{matrix}

munkát végzünk. A teljes energia ezen munkák összege:

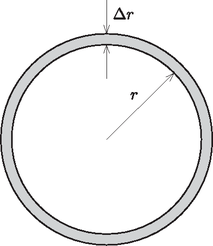\begin{matrix} E_{grav} = \sum Δ W = - γ ϱ^{2} \frac{16 π^{2}}{3} \int_{0}^{R} r^{4} d r = - \frac{3}{5} \cdot γ \frac{M^{2}}{R} . \end{matrix}

5. ábra

Megjegyzés. A gravitáció és az elektrosztatika egyenletei közötti hasonlóság felismerésével, majd az

\frac{1}{2} ε_{0} E^{2}

energiasűrűség integrálásával ugyanerre az eredményre juthatunk.

3.2. Az elektron lehetséges hullámhosszaira (a kocka mindhárom oldalélével párhuzamos irányban) a következő feltétel teljesül (6. ábra):

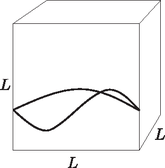\begin{matrix} n \frac{λ}{2} = L (aholnpozitív egész) . \end{matrix}

6. ábra

A hullámhossz és az impulzus közötti kapcsolatot a de Broglie-féle

λ = h / p

összefüggés adja meg. Az elektron lehetséges impulzuskomponensei tehát

\begin{matrix} p_{x} = \pm \frac{n_{x} h}{2 L}; p_{y} = \pm \frac{n_{y} h}{2 L}; p_{z} = \pm \frac{n_{z} h}{2 L}, \end{matrix}

ahol

n_{x}

n_{y}

és

n_{z}

pozitív egészek.

3.3. Az elektron energiája

\begin{matrix} E = \sqrt[]{p_{x}^{2} + p_{y}^{2} + p_{z}^{2}}, \end{matrix}

így alapállapotban az összes elektron egy

\begin{matrix} p_{{max}_{}^{}} = \sqrt[]{2 m_{e} E_{{max}_{}^{}}} \end{matrix}

sugarú gömbön belül helyezkedik el a

p

vektor komponensei által ,,kifeszített'' ún. impulzustérben (lásd a 7. ábrát, amelyen az áttekinthetőség kedvéért csak két dimenzióban ábrázoltuk az elektronállapotokat). Egy-egy elektronállapot

{(\frac{h}{2 L})}^{3}

térfogatot foglal el az impulzustérben, így az elektronállapotok száma (jó közelítéssel)

\begin{matrix} N = 2 \cdot \frac{\frac{4}{3} π p_{{max}_{}^{}}^{3}}{{(\frac{h}{2 L})}^{3}} . \end{matrix}

(A jobb oldalon a 2-es faktor a Pauli-elv miatt jelent meg.) Ebből

p_{{max}_{}^{}}

értéke

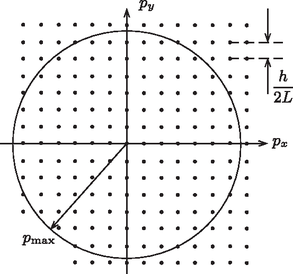\begin{matrix} p_{{max}_{}^{}} = \frac{h}{4 L} {(\frac{3}{π} N)}^{1 / 3} . \end{matrix}

7. ábra

3.4. Az impulzustérben a

p

sugarú,

Δ p

vastagságú gömbhéjban lévő elektronállapotok száma:

\begin{matrix} Δ N = 2 \frac{4 π p^{2}}{{(\frac{h}{2 L})}^{3}} Δ p . \end{matrix}

(A 2-es faktor a jobb oldalon ismét a Pauli-elv miatt szerepel.) Ebben a héjban mindegyik elektron energiája

\frac{p^{2}}{(2 m_{e})}

, ezért a héj összes energiája

\begin{matrix} Δ E = \frac{8 π p^{2}}{{(\frac{h}{2 L})}^{3}} Δ p \cdot \frac{p^{2}}{(2 m_{e})} = \frac{32 π L^{3}}{h^{3} m_{e}} p^{4} Δ p . \end{matrix}

A teljes elektronrendszer energiája tehát

\begin{matrix} E_{N} = \frac{32 π L^{3}}{h^{3} m_{e}} \int_{0}^{p_{{max}_{}^{}}} p^{4} d p = \frac{32 π L^{3}}{h^{3} m_{e}} \cdot \frac{p_{{max}_{}^{}}^{5}}{5} = \frac{32 π}{5} {(\frac{3}{64 π})}^{5 / 3} \cdot \frac{h^{2}}{m_{e}} \cdot N^{\frac{5}{3}} \cdot L^{- 2} . \end{matrix}

Leolvashatjuk, hogy a keresett dimenziótlan állandók:

\begin{matrix} α = \frac{32 π}{5} {(\frac{3}{64 π})}^{5 / 3} \approx 0, 018; β = \frac{5}{3}; γ = - 2. \end{matrix}

3.5. A csillag teljes energiája

\begin{matrix} E_{teljes} = E_{grav} + E_{N} = - \frac{3}{5} γ \frac{M^{2}}{R} + α' \frac{h^{2}}{m_{e}} N^{5 / 3} R^{- 2}, ahol α' = \frac{3}{10 \cdot 2^{2 / 3}} {(\frac{3}{4 π})}^{4 / 3} . \end{matrix}

A csillag egyensúlyi állapotát az

E_{teljes} (R)

függvény minimuma adja meg. A szélsőértékhez tartozó

R_{ft}

csillagsugarat deriválással, vagy

E_{teljes} (R)

(ami az

1 / R

változó másodfokú függvénye) teljes négyzetté alakításával lehet meghatározni. A fehér törpe egyensúlyi sugarára így az

\begin{matrix} R_{ft} = \frac{10}{3} \frac{h 161; N^{5 / 3} α'}{γ M^{2} m_{e}} \end{matrix}

kifejezést kapjuk. Mivel a csillag össztöltése 0,

N

nemcsak az elektronok, hanem a protonok számával is egyenlő. A csillag össztömegét lényegében a benne lévő (egyenként

m_{p}

tömegű) protonok adják, így

N \approx M / m_{p}

. Ezt felhasználva és az ismert adatokat behelyettesítve végül megkapjuk a Naphoz hasonló tömegű fehér törpe sugarát:

\begin{matrix} R_{ft} = \frac{10}{3} \frac{h 161; α'}{γ M^{1 / 3} m_{e} m_{p}^{5 / 3}} = \frac{1}{2^{2 / 3}} {(\frac{3}{4 π})}^{4 / 3} \frac{h^{2}}{γ M^{1 / 3} m_{e} m_{p}^{5 / 3}} \approx 22 800 km . \end{matrix}

¹A feladatok szövegét múlt havi számunkban közöltük.