Kezdőlap


Cím:	Kunfalvi Rezső Olimpiai Válogatóverseny
Füzet:	2015/szeptember, 365 - 370. oldal	PDF \| MathML
Témakör(ök):	Nemzetközi Fizika Diákolimpia

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

¹
1. forduló, elméleti rész²

1. feladat. (Ez a feladat három független, kisebb részből áll.) (150 p)

1.A. Egy függőleges tengelyű mérőhenger falába sűrűn, egyenletes elrendezésben apró lyukakat fúrtunk. A hengert

H

magasságig feltöltjük vízzel, melynek következtében a lyukakon (a mérőhenger falára merőlegesen) vékony vízsugarak lövellnek ki. Milyen alakú a vízsugarak burkolófelülete? (A vízsugarak nem akadályozzák egymást, és folyamatos utántöltéssel gondoskodunk a hengerben a vízszint állandóságáról.) (50 p)

1.B. Hőszigetelt hengert egy könnyen mozgó, hőszigetelő dugattyú oszt két részre az 1. ábrán látható módon. A két rekeszben azonos anyagmennyiségű és (kezdetben) azonos hőmérsékletű héliumgáz van. A bal oldali térrészben lévő gázt egy fűtőszál segítségével lassan melegíteni kezdjük. Mekkora ebben a folyamatban a bal oldali gáz mólhője, amikor a dugattyú elmozdulása még kicsi? (50 p)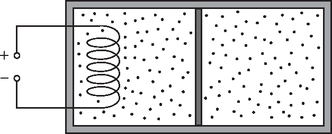

1. ábra

1.C. Egy nagyméretű, négyzet alakú, vékony fémlemez anyagának fajlagos ellenállását szeretnénk megmérni. Ehhez a lemez egyik csúcsának közelében kiválasztjuk a két szomszédos oldalélen található

A

B

C

és

D

pontokat a 2. ábrán látható módon. (Az

A

és

B

pontok távolsága a kiválasztott csúcstól

2 d

, a

C

és

D

pontoké pedig

d

, ahol

d

sokkal kisebb a fémlemez oldalhosszánál.)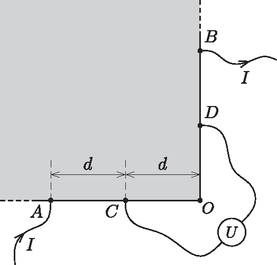

2. ábra

Ha az

A

pontba

I

erősségű áramot vezetünk, a

B

pontból pedig elvezetjük azt, akkor a

C

és

D

pontok közé kapcsolt voltmérő

U

feszültséget jelez. Határozzuk meg a fémlemez

ϱ

fajlagos ellenállását, ha tudjuk, hogy a lemez vastagsága

δ

! (50 p)

2. feladat. Furfangos szökőkút (150 p)

Köztereken, parkokban gyakran láthatunk olyan szökőkutat, amely ,,vízen úszó'' gránitgömbből vagy gránithengerből áll (lásd a 3. ábrát). Az ilyen szökőkutak felépítése a következő: a (rendszerint tömör) gránitgömb vagy gránithenger egy jól illeszkedő vályúban található, melynek alján rés van. A résen keresztül egy szivattyú folyamatosan vizet pumpál a vályúba, amely a vályú pereménél kifolyik. A gránittömb és a vályú között vékony (általában 1‐2 milliméter vastagságú) vízréteg alakul ki, így a gránit nem érintkezik a vályú falával, csak a vízzel. Vajon hogyan képes megtartani a víz a nála sokkal nagyobb sűrűségű gránittömb súlyát? Ez a feladat ezzel a kérdéssel foglalkozik.

3. ábra

Az egyszerűség kedvéért a gránittömböt egy

L

hosszúságú,

R

sugarú,

ϱ

sűrűségű tömör hengernek tekintjük, ahol

L ≫ R

. A vályú alján található befolyónyílás legyen egy

L

hosszúságú, keskeny rés, így a feladat során elegendő csupán a 4. ábrán látható síkmetszetben vizsgálódnunk. A vályú magasságát a

θ_{max}

szöggel jellemezhetjük. A résen áthaladó vízhozamot az időegység alatt befolyó víz térfogatával írhatjuk le, amely időben állandó:

\begin{matrix} Q_{be} \equiv \frac{Δ V}{Δ t} . \end{matrix}

A feladatban vizsgált konkrét szökőkútnál legyen

L = 2 m

R = 0, 3

θ_{{max}_{}^{}} = 30^{\circ}

; a gránit

ϱ

sűrűsége pedig a víz

ϱ_{víz}

sűrűségének

2, 75

-szerese.

4. ábra

2.1. A víz hidrosztatikai felhajtóereje nyilván nem képes megtartani a gránithenger súlyát. Adjuk meg a felhajtóerő és a gránithengerre ható nehézségi erő hányadosát

ϱ

ϱ_{víz}

és

θ_{max}

segítségével, majd adjuk meg az eredményt számszerűen is! (10 p)
A továbbiakban a felhajtóerő szerepét hanyagoljuk el! A gránithengert megtartó erő megértéséhez figyelembe kell vennünk az áramló víz belső súrlódását. Ehhez tekintsünk egy folyadékot, amely két vízszintes, párhuzamos, egymástól

h

távolságra lévő síklap között lassan áramlik

x

irányban (lásd az 5. ábrát).

5. ábra

Ha két szomszédos folyadékréteg (például az 5. ábrán látható, az alsó síklaptól

z

és

z + Δ z

távolságra található rétegek) különböző sebességgel mozog, akkor közöttük a

Δ v

relatív sebességükkel és az érintkezési felületük nagyságával arányos súrlódási erő ébred (Newton-féle súrlódási törvény):

\begin{matrix} F = η A \frac{Δ v}{Δ z}, \end{matrix}

(1)

ahol

η

a folyadék anyagára jellemző állandó, a viszkozitás. Ez az erő benne van a folyadékok érintkezési felületének síkjában, és a relatív sebességgel ellentétes irányba mutat. A

σ = F / A

mennyiséget nyírófeszültségnek nevezzük.

2.2. Mivel a folyadék

z

irányban nem áramlik, így ebben az irányban nem hat nyírófeszültség, ezért a folyadékban a nyomás csak az

x

koordinátától függ,

z

-től nem. Mutassuk meg, hogy stacionárius (időben állandó) áramlás esetén a

σ (z)

nyírófeszültség térbeli változása (gradiense) és a

p (x)

nyomás gradiense között fennáll a

\begin{matrix} \frac{Δ p}{Δ x} = \frac{Δ σ}{Δ z} \end{matrix}

(2)

összefüggés. (20 p)

2.3. A

(2)

egyenlet bal oldala csak

x

-től, jobb oldala pedig csak

z

-től függ, ezért mindkét oldalnak külön-külön állandónak kell lennie. Jelöljük ezt az állandót

- K

-val, ahol

K

pozitív mennyiség:

\begin{matrix} \frac{Δ p}{Δ x} = \frac{Δ σ}{Δ z} = - K . \end{matrix}

Lássuk be, hogy a síklapok között a folyadék sebessége a

\begin{matrix} v (z) = A z^{2} + B z + C \end{matrix}

(3)

függvénnyel írható le, és határozzuk meg az

A

B

és

C

konstansok értékét

η

h

és

K

segítségével! (A folyadék sebessége a síklapoknál nulla.) (25 p)

2.4. A szökőkút esetében a vízréteg vastagsága sokkal kisebb a gránithenger sugaránál, ezért használhatjuk a 2.2‐2.3 részfeladatokban kapott eredményeket. Határozzuk meg, mekkorának kell lennie a túlnyomásnak a vályú alján (a víz beáramlási pontjánál) ahhoz, hogy a gránithenger egyensúlyban legyen! Válaszunkat

ϱ

R

θ_{{max}_{}^{}}

és a

g

nehézségi gyorsulás segítségével adjuk meg! (Számításainkban a hengerre érintőirányban ható nyírófeszültség hatását és a Bernoulli-törvényből származó nyomáscsökkenést hanyagoljuk el.) (30 p)

2.5. Határozzuk meg a vályú alján található nyíláson beáramló víz

Q_{be}

hozamát, ha ismert, hogy a vályú és a gránithenger közötti vízréteg vastagsága

h

. A választ az

η

ϱ

θ_{{max}_{}^{}}

g

L

és

h

mennyiségek felhasználásával adjuk meg. (25 p)

2.6. Ha a gránithengert tengelye körül forgásba hozzuk, a 2.3. részfeladatban a víz sebességprofiljára kapott

(3)

formulát módosítani kell egy

z

-vel egyenesen arányos tag hozzáadásával: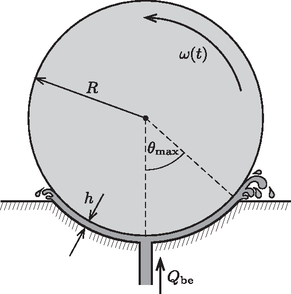

\begin{matrix} v (z, ω) = v (z) \pm D z, \end{matrix}

ahol

v (z, ω)

a henger

ω

szögsebességétől függő sebességprofil,

D

a szögsebességet tartalmazó arányossági tényező, a

\pm

előjel pedig a henger két oldalán áramló folyadékrészre utal. Fejezzük ki

D

értékét

ω

R

és

h

segítségével, ha továbbra is fennáll, hogy a víz falakhoz viszonyított relatív sebessége zérus. (15 p)

6. ábra

2.7. Forgás közben a víz által kifejtett nyírófeszültség fékezi a gránithengert. Milyen mozgást végez ekkor a henger? Adjuk meg a henger szögsebességét az idő függvényében, ha a kezdeti szögsebessége

ω_{0}

. A választ

ϱ

R

h

θ_{{max}_{}^{}}

ω_{0}

és

η

segítségével adjuk meg! (25 p)

3. feladat. Fehér törpék keletkezése (150 p)
A Naphoz hasonló, életük derekán járó csillagok stabil objektumok. A csillag belsejében magfúzió útján folyamatosan termelődő energia igyekezne a csillag anyagát kifelé lökni; ez az effektus akadályozza meg a gravitációs összeomlást és tartja fenn a stabil egyensúlyt. Az egyensúlyi állapot mindaddig fennáll, amíg el nem fogy az összes hidrogén: ekkor a gravitációs vonzás elkezdi összeroppantani a csillagot. A Nappal megegyező (vagy ahhoz közeli) tömegű csillagok esetében ez az összeroskadás nem tart örökké: a fehér törpe állapot elérésével a csillag stabilizálódik, az összeroppanás befejeződik. Ez a feladat a fehér törpék keletkezésének fizikájával foglalkozik.

3.1. Vizsgáljunk egy gömb alakú,

R

sugarú,

M

tömegű csillagot. Az egyszerűség kedvéért tegyük fel, hogy a csillag tömegeloszlása egyenletes. Határozzuk meg a csillag teljes

E_{grav}

gravitációs energiáját! (30 p)
A magfúzió leállásakor a gravitáció összehúzó hatását kezdetben semmi sem tudja ellensúlyozni, ezért a csillag sugara csökkenni kezd. Ez a folyamat azonban egy kvantummechanikai hatásnak (a csillagban lévő elektronok ún. degenerációs nyomásának) köszönhetően megállhat, és a csillag stabil végállapotba kerülhet (fehér törpe). A 3.2.‐3.4. részfeladatok a degenerációs nyomás fizikai okával foglalkoznak.

3.2. Tekintsünk egy

L

oldalélű, kocka alakú dobozba zárt elektront. A derékszögű koordináta-rendszerünk tengelyeit válasszuk a kocka oldaléleivel párhuzamosnak. Adjuk meg az elektron

(p_{x}, p_{y}, p_{z})

impulzuskomponenseinek lehetséges értékeit

L

és a

h

Planck-állandó segítségével! (20 p)

3.3. Ha a 3.2. részfeladatban szereplő kocka alakú dobozba nem egy, hanem

N

darab (

N ≫ 1

) elektront helyezünk, akkor alapállapotban az elektronok a lehetséges legalacsonyabb energiájú állapotokat töltik be. (Most és a továbbiakban az elektronok közötti Coulomb-kölcsönhatást hanyagoljuk el, mert az a kvantumos viselkedésből származó erőhatásnál sokkal gyengébb.) A Pauli-elv értelmében azonban egyszerre legfeljebb két elektron lehet ugyanabban a

(p_{x}, p_{y}, p_{z})

számhármassal jellemzett kvantumállapotban. Mutassuk meg, hogy alapállapotban azok az elektronállapotok betöltöttek, melyek impulzusára fennáll a

\sqrt[]{p_{x}^{2} + p_{y}^{2} + p_{z}^{2}} \leq p_{{max}_{}^{}}

egyenlőtlenség, és adjuk meg

p_{max}

(közelítő) értékét

L

és

N

függvényében! (30 p)

3.4. Mutassuk meg, hogy ekkor az

N

elektront tartalmazó rendszer teljes (kinetikus) energiája

\begin{matrix} E_{N} = α \cdot \frac{h^{2}}{m_{e}} N^{β} L^{γ} \end{matrix}

alakú, ahol

α

β

és

γ

dimenziótlan konstansok. Határozzuk meg ezen konstansok számszerű értékét! (Vegyük figyelembe, hogy

N

nagy, ezért a szummázást integrállal közelíthetjük. A kocka alakú doboz mérete elegendően nagy ahhoz, hogy a bezárt elektronok viselkedése nemrelativisztikus legyen.) (40 p)
Mivel a csillagok nem kocka alakúak, a degenerációs energia pontos kiszámításához a 3.4. részfeladatban kapott egyenlet kis változtatásra szorul.

L

helyére a csillag

R

sugarát helyettesítve, valamint

α

értékét módosítva azonban helyes formulához jutunk:

\begin{matrix} E_{N} = \frac{3}{10 \cdot 2^{2 / 3}} {(\frac{3}{4 π})}^{4 / 3} \frac{h^{2}}{m_{e}} N^{β} R^{γ}, \end{matrix}

ahol

β

és

γ

a korábban kapott értékek,

N

pedig az elektronok száma. (A csillag összességében semleges, és feltehetjük, hogy ugyanannyi protont tartalmaz, mint elektront. A protonok is létrehoznak degenerációs nyomást, ez azonban a nagy tömegük miatt sokkal kisebb, mint az elektronok járuléka, ezért elhanyagolható.)

3.5. A csillag teljes energiája az

E_{grav}

gravitációs energia és az

E_{N}

degenerációs energia összege. Írjuk fel a teljes energiát a csillag sugarának függvényében, majd határozzuk meg a csillag végső, egyensúlyi

R_{ft}

sugarát, az úgynevezett fehér törpe rádiuszt! Számítsuk is ki számszerű értékét a Nap esetére! (30 p)

Fizikai állandók táblázata

\begin{matrix} univerzális gázállandó: & R = 8, 314 J / (mol \cdot K) \\ gravitációs állandó: & G = 6, 67 \cdot 10^{- 11}m^{3}/(kg s^{2}) \\ Planck-állandó: & h = 6, 626 \cdot 10^{- 34}Js \\ elektron tömege: & m_{e} = 9, 109 \cdot 10^{- 31}kg \\ proton tömege: & m_{p} = 1, 673 \cdot 10^{- 27}kg \\ a Nap tömege: & M_{⊙} = 1, 989 \cdot 10^{30}kg \end{matrix}

Hasznos matematikai összefüggések

\begin{matrix} \int x^{n} d x = \frac{x^{n + 1}}{n + 1} + C (n \neq - 1); \int \frac{1}{x} d x = ln | x | + C; \\ \int cos x d x = sin x + C; \int x cos x d x = x sin x + cos x + C . \end{matrix}

¹Kunfalvi Rezső (1905‐1998) a Nemzetközi Fizikai Diákolimpiák egyik alapítója és sok éven keresztül a magyar csapat felkészítője, vezetője volt. 1959-től 1975-ig ő szerkesztette a KöMaL (korábban KML) fizika ,,rovatát''. Emlékét az olimpiai válogatóverseny is őrzi.

²Az elméleti forduló időtartama 4 óra volt. A feladatok hibátlan megoldásával összesen 450 pontot lehetett szerezni. Az összes feladathoz egyetlen, közös adattáblázat tartozik (lásd a feladatsor végét), ami a feladatokban szereplő konstansokat, fizikai állandókat és hasznos matematikai összefüggéseket tartalmazza.
A feladatok megoldásához író- és rajzeszközökön, valamint kétsoros (nem grafikus) számológépen kívül semmilyen segédeszköz (könyv, füzet, internet, számítógép, mobiltelefon stb.) nem volt használható.
A verseny igyekezett követni a Nemzetközi Fizikai Diákolimpia elméleti versenyeinek stílusát, nehézségi fokát, és azok formai követelményeihez igazodott.
A feladatokat Vigh Máté (ELTE), a magyar csapat egyik felkészítője állította össze.
A feladatok megoldását a jövő havi számunkban közöljük.