Cím:	Megoldásvázlatok a 2014/1. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Czinki József
Füzet:	2014/február, 73 - 84. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Zsebszámológép használata nélkül adjuk meg a következő kifejezés értékét: $\begin{array}{c}{\displaystyle \frac{2010201120122010\cdot 2010201120122016}{2010201120122015}:\left(1-\frac{5}{2010201120122015}\right)\mathrm{.}}\end{array}$ $b)$ Milyen $k$ valós számok esetén van a $k{x}^2-3x^2-k\left(2x-6\right)=0$ egyenletnek pozitív valós gyöke?  (11 pont)   Megoldás. $a)$ Legyen $a=2010201120122013$. Ekkor a kifejezés így írható: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{\left(a-3\right)\cdot \left(a+3\right)}{a+2}:\left(1-\frac{5}{a+2}\right)}& {\displaystyle =\frac{\left(a-3\right)\cdot \left(a+3\right)}{a+2}:\frac{a+2-5}{a+2}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{\left(a-3\right)\cdot \left(a+3\right)}{a+2}\cdot \frac{a+2}{a-3}=a+3.}\hfill \end{array}}$ Vagyis a kifejezés értéke: 2 010 201 120 122 016. $b)$ Átalakítva az egyenletet, kapjuk: $\left(k-3\right)x^2-2kx+6k=0$. I. Ha $k=3$, akkor az egyenlet elsőfokú, megoldása $x=3$, ami pozitív. II. Ha $k\ne 3$, akkor az egyenlet másodfokú. II.1. Két különböző valós gyöke van az egyenletnek, ha a diszkriminánsa pozitív: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(-2k\right)}^2-4\cdot \left(k-3\right)\cdot 6k}& {\displaystyle >\mathrm{0,}}\hfill \\ \hfill {\displaystyle 4k^2-24k^2+72k}& {\displaystyle >\mathrm{0,}}\hfill \\ \hfill {\displaystyle -5k^2+18k}& {\displaystyle >\mathrm{0,}}\hfill \\ \hfill {\displaystyle k\left(5k-18\right)}& {\displaystyle <0.}\hfill \end{array}}$ Az egyenlőtlenség megoldása: $k\in ]0;\frac{18}{5}[$. II.1.1. Két pozitív gyöke van az egyenletnek, ha $k\in ]0;\frac{18}{5}[$, és ezen kívül teljesül: $\begin{array}{c}{\displaystyle x_1{x}_2=\frac{6k}{k-3}>0\text{és}{x}_1+x_2=-\frac{-2k}{k-3}>0.}\end{array}$ Mindkét egyenlőtlenség megoldása a $k\in \left]-\infty ;0\right[\cup \left]3;+\infty \right[$. Mindent egybevetve az egyenletnek két különböző pozitív gyöke van, ha $k\in ]3;\frac{18}{5}[$. II.1.2. Egy pozitív és egy negatív valós gyöke van az egyenletnek, ha $k\in ]0;\frac{18}{5}[$ és ezen kívül teljesül: $\begin{array}{c}{\displaystyle x_1{x}_2=\frac{6k}{k-3}<0.}\end{array}$ Mivel az egyenlőtlenség megoldása: $k\in \left]0;3\right[$, adódik, hogy az egyenletnek egy pozitív és egy negatív gyöke van, ha $k\in \left]0;3\right[$. II.1.3. Egy pozitív és egy 0 valós gyöke nem lehet az egyenletnek. Ehhez a $k=0$ szükséges feltétel kellene, de ekkor mindkét gyök 0 lenne. II.2. Két egybeeső valós gyöke van az egyenletnek, ha a diszkriminánsa 0, vagyis: $\begin{array}{c}{\displaystyle k\left(5k-18\right)=0.}\end{array}$ Ez $k=0$, illetve $k=\frac{18}{5}$ esetén áll fenn. Ha $k=0$, akkor a $\left(k-3\right)x^2-2kx+6k=0$ egyenlet a $-3x^2=0$ alakot ölti. Ekkor a két egybeeső gyök: $x_{\mathrm{1,2}}=0$. Ha $k=\frac{18}{5}$, akkor az egyenlet a  $\begin{array}{c}{\displaystyle \frac{3}{5}{x}^2-\frac{36}{5}x+\frac{108}{5}=0}\end{array}$ alakot ölti. Ezt a következő alakra hozhatjuk: $x^2-12x+36={\left(x-6\right)}^2=0$. Ekkor a két egybeeső gyök: $x_{\mathrm{1,2}}=6$. Összefoglalva: az egyenletnek akkor van pozitív valós gyöke, ha $k\in ]0;\frac{18}{5}]$.   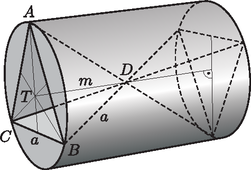2. Egy henger alakú rézalkatrészből hiányzik az ábrán látható módon két darab 4 cm élű szabályos tetraéder alakú rész. A gyártó cégtől 65 000 darab ilyen alkatrészt rendeltek meg. Hány tonna rezet rendeljen a cég, ha a gyártás során fellépő veszteségek miatt a szükséges mennyiségnél 15%-kal több rezet kell felhasználniuk? (A réz sűrűsége 8960 kg/m${}^3$.)  (12 pont)       Megoldás. Az $ABCD$ szabályos tetraéder $ABC$ alapháromszögében bármely súlyvonal kétharmad részét számolva a henger alapkörének $CT$ sugarát kapjuk. $\begin{array}{c}{\displaystyle CT=a\cdot \frac{\sqrt[]{3}}{2}\cdot \frac{2}{3}=\frac{4\sqrt[]{3}}{3}\mathrm{.}}\end{array}$ A $CTD$ derékszögű háromszögből Pitagorasz-tétellel számolható a $TD$ szakasz hossza, amely a tetraéder magassága, és egyben a henger magasságának a fele is: $\begin{array}{c}{\displaystyle TD=\sqrt[]{a^2-{CT}^2}=\sqrt[]{16-\frac{16\cdot 3}{9}}=\sqrt[]{\frac{32}{3}}=4\cdot \sqrt[]{\frac{2}{3}}\mathrm{.}}\end{array}$ Az $ABCD$ szabályos tetraéder térfogata: $\begin{array}{c}{\displaystyle V_{ABCD}=\frac{\frac{a^2\sqrt[]{3}}{4}\cdot TD}{3}=\frac{\frac{16\sqrt[]{3}}{4}\cdot 4\cdot \sqrt[]{\frac{2}{3}}}{3}=\frac{16\sqrt[]{2}}{3}\approx 7\mathrm{,}54.}\end{array}$ A henger térfogata: $\begin{array}{c}{\displaystyle V_{\text{henger}}={CT}^2\cdot \pi \cdot 2\cdot TD={\left(\frac{4\sqrt[]{3}}{3}\right)}^2\cdot \pi \cdot 8\cdot \sqrt[]{\frac{2}{3}}=\frac{128}{3}\cdot \sqrt[]{\frac{2}{3}}\cdot \pi \approx 109\mathrm{,}44.}\end{array}$ A test térfogata: $\begin{array}{c}{\displaystyle V_{\text{henger}}-2\cdot V_{ABCD}=109\mathrm{,}44-2\cdot 7\mathrm{,}54=94\mathrm{,}36\left({\text{cm}}^3\right)\mathrm{.}}\end{array}$ 65 000 darab ilyen test térfogata: $65000\cdot 94\mathrm{,}36{\text{cm}}^3=6133400{\text{cm}}^3=6\mathrm{,}1334{\text{m}}^3$. A 15%-os ráhagyással együtt: $6\mathrm{,}1334{\text{m}}^3\cdot 1\mathrm{,}15=7\mathrm{,}05341{\text{m}}^3$. Ennek a térfogatnak megfelelő tömeg: $\begin{array}{c}{\displaystyle 7\mathrm{,}05341{\text{m}}^3\cdot 8960\frac{\text{kg}}{{\text{m}}^3}\approx 63198\mathrm{,}6\text{kg}\approx 63\mathrm{,}2\text{t}\mathrm{.}}\end{array}$ Vagyis kb. 63,2 tonna rezet kell rendelnie a cégnek.   3. $a)$ Az $a$-val és $b$-vel prímszámok négyzeteit jelöljük. Mennyi az $a$ és $b$ értéke, ha a $\sqrt[]{a}-\sqrt[]{2b}$ és $\sqrt[]{a}+\sqrt[]{2b}$ kifejezések egymás reciprokai? $b)$ Mutassuk meg, hogy $10\mid 2^{2014}+2^{2015}+2^{2016}+2^{2017}$. $c)$ Mutassuk meg, hogy $11\mid {100}^{2014}-1$.  (14 pont)   Megoldás. $a)$ Ha két kifejezés egymás reciproka, akkor szorzatuk 1, vagyis felírható: $\begin{array}{c}{\displaystyle \left(\sqrt[]{a}-\sqrt[]{2b}\right)\cdot \left(\sqrt[]{a}+\sqrt[]{2b}\right)=1.}\end{array}$ Alkalmazva az ismert azonosságot kapjuk: $\begin{array}{c}{\displaystyle a-2b=1.}\end{array}$ Vegyük észre, hogy $a$ páratlan (mivel páros számot vonunk ki belőle és 1-et kapunk), vagyis $a$ egy páratlan prímszám négyzete. Átrendezve az egyenletet, kapjuk: $a-1=2b$. Az egyenlet bal oldala osztható néggyel, hiszen páratlan szám négyzete néggyel osztva 1 maradékot ad. Ebből adódik, hogy $2b$ osztható néggyel, vagyis $b$ osztható kettővel. Prímszám négyzete csak akkor lehet osztható 2-vel, ha az a 2-nek a négyzete. Vagyis $b=4$, és ebből adódik, hogy $a=9$. $b)$ Tudjuk, hogy a $2^{\alpha }$ (ahol $\alpha$ pozitív természetes szám) hatvány utolsó számjegye: $\begin{array}{c}\end{array}$2, ha $\alpha$ néggyel osztva 1 maradékot ad; $\begin{array}{c}\end{array}$4, ha $\alpha$ néggyel osztva 2 maradékot ad; $\begin{array}{c}\end{array}$8, ha $\alpha$ néggyel osztva 3 maradékot ad; $\begin{array}{c}\end{array}$6, ha $\alpha$ néggyel osztható. Ebből adódóan a $2^{2014}+2^{2015}+2^{2016}+2^{2017}$összegben a tagok utolsó számjegyei meghatározhatók.   ${\displaystyle \begin{array}{|ccccc|}\hline \hfill {\displaystyle \text{hatvány}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>2</mn></mrow><mrow><mn>2014</mn></mrow></msup></mrow></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>2</mn></mrow><mrow><mn>2015</mn></mrow></msup></mrow></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>2</mn></mrow><mrow><mn>2016</mn></mrow></msup></mrow></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>2</mn></mrow><mrow><mn>2017</mn></mrow></msup></mrow></math> }}\hfill \\ \hfill {\displaystyle \text{végződés}}\hfill & \hfill {\displaystyle \text{ 4}}\hfill & \hfill {\displaystyle \text{ 8}}\hfill & \hfill {\displaystyle \text{ 6}}\hfill & \hfill {\displaystyle \text{2 }}\hfill \\ \hline\end{array}}$   A végződések összege: $4+8+6+2=20$. Mivel természetes számok összegének utolsó számjegyét a tagok utolsó számjegyei összegének az utolsó számjegye határozza meg, azért a $2^{2014}+2^{2015}+2^{2016}+2^{2017}$ összeg a tízes számrendszerben 0-ra végződik, tehát osztható 10-zel. $c)$ Ha a ${100}^{2014}$ számot leírnánk, akkor egy darab 1-esre és utána 4028 darab 0-ra lenne szükségünk. Ha ebből a számból kivonunk 1-et, akkor egy olyan számot kapunk, amelyben 4028 darab 9-es szerepel: $\begin{array}{c}{\displaystyle {100}^{2014}-1=\underset{\text{4028 db}}{\overset{}{\underbrace{9999\text{...}99}}}\mathrm{.}}\end{array}$ Ha elvégezzük az osztást, akkor látható lesz, hogy ez a 4028 jegyű szám valóban osztható 11-gyel: $\begin{array}{c}{\displaystyle \underset{\text{4028 db}}{\overset{}{\underbrace{9999\text{...}99}}}:11=\underset{\text{4027 db számjegy}}{\overset{}{\underbrace{90909\text{...}909}}}\mathrm{.}}\end{array}$   Megjegyzés. Használhatjuk a 11-es oszthatósági szabályt is. Könnyű belátni, hogy a szám páratlan helyiértékein lévő számjegyeinek összege (ami 2014 darab 9-es), ugyanannyi, mint a páros helyiértékein lévő számjegyek összege (ami szintén 2014 darab 9-es). Ez azt jelenti, hogy ${100}^{2014}-1$ osztható 11-gyel.   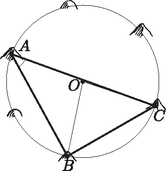4. $a)$ Egy ősi kultikus helyen több tonnás kőtömbök vannak elhelyezve egy körvonal mentén. Egy régész a következő módon határozta meg a kör sugarát: kiválasztott egy $A$ kőtömböt, és megmérte a távolságát egy $B$, illetve egy $C$ kőtömbtől. A mérések eredményeként 184 m és 241 m adódott. Majd megmérte, hogy az $A$ kőtömb helyéről a $B$ és a $C$ kőtömb által meghatározott szakasz milyen szögben látszik. A mérés szerint ez a szög ${41}^{\circ }23\text{'}$ nagyságú. Számoljuk ki mi is a kör sugarát. $b)$ Milyen távol van az $a)$ feladatrészben szereplő kultikus kör középpontjától az a fa, amely éppen ott áll, ahol a körhöz a $B$ és a $C$ pontokban húzott érintőegyenesek metszik egymást?  (14 pont)   Megoldás. $a)$ Az $ABC$ háromszögből koszinusztétellel számolható a $BC$ szakasz hossza: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {BC}^2}& {\displaystyle ={AC}^2+{AB}^2-2\cdot AC\cdot AB\cdot \text{cos}\left(CAB\sphericalangle \right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={241}^2+{184}^2-2\cdot 241\cdot 184\cdot \text{cos}{41}^{\circ }23\text{'}\approx 25394\mathrm{,}09.}\hfill \end{array}}$ Ebből adódik: $BC\approx 159\mathrm{,}36$.     Alkalmazzuk az $a=2r\text{sin}\alpha$ összefüggést: $\begin{array}{c}{\displaystyle 159\mathrm{,}36=2r\cdot \text{sin}{41}^{\circ }23\text{'}\mathrm{.}}\end{array}$ Ebből a kör sugara: $r=OC\approx 120\mathrm{,}53$ m. 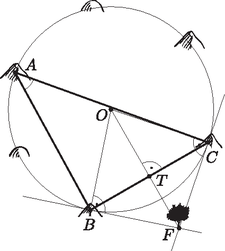$b)$ A körhöz a $B$ és a $C$ pontokban húzott érintőegyenesek metszéspontja legyen $F$. Mivel a külső pontból a körhöz húzott érintőszakaszok egyenlők, azért $CF=BF$, továbbá $OC=OB$, mivel ezek a kör sugarai. Vagyis az $OCFB$ négyszög deltoid, és $OF$ a szimmetriaátlója. Ennek a szakasznak a hosszát keressük. (Tehát az $O$ pont, a $T$ pont, vagyis a $BC$ húr felezőpontja és az $F$ pont egy egyenesre esnek.) A középponti és a kerületi szögek közötti összefüggés alapján: $\begin{array}{c}{\displaystyle COT\sphericalangle =\frac{1}{2}\cdot COB\sphericalangle =CAB\sphericalangle ={41}^{\circ }23\text{'}\mathrm{.}}\end{array}$     Mivel a kör érintője merőleges az adott pontba húzott sugárra, azért az $OCF$ háromszög derékszögű, tehát felírható: $\begin{array}{c}{\displaystyle \frac{OC}{OF}=\frac{120\mathrm{,}53}{OF}=\text{cos}{41}^{\circ }23\text{'}\mathrm{.}}\end{array}$ Ebből $OF\approx 160\mathrm{,}64$ méter adódik. Vagyis a fa kb. 160,64 méterre van a kör középpontjától.   II. rész     5. $a)$ Egy hordóban alkohol vizes oldatából $10$ litert tároltunk. Először kivettünk belőle két litert, amit két liter tiszta vízzel pótoltunk. Majd kivettünk belőle $1$ litert. Végül hozzáadtunk $6$ liter alkoholt, amely $77$ térfogatszázalékos vizes oldat volt. Így $50$ térfogatszázalékos vizes oldatot kaptunk. Hány térfogatszázalékos volt az eredeti oldat? $($Egy oldat térfogatszázaléka: $\frac{\text{oldott anyag térfogata}}{\text{oldat térfogata}}\cdot 100$.) $b)$ Oldjuk meg a  $\begin{array}{c}{\displaystyle \text{cos}x={\left(x-2\pi \right)}^2+1}\end{array}$ egyenletet. $c)$ A radioaktív bomlási törvény $\begin{array}{c}{\displaystyle N=N_0\cdot {\left(\frac{1}{2}\right)}^{\frac{t}{T}}}\end{array}$ megadja, hogy a $T$ felezési idejű és kezdetben $N_0$ számú atommagot tartalmazó radioaktív anyagból $t$ idő eltelte után mennyi a megmaradt el nem bomlott atommagok $N$ száma. Egy ősrégi növényi kövület esetén megmérték, hogy jelenleg benne a ${}^{14}\text{C}$ szénizotóp koncentrációja $65$ százaléka annak a ${}^{14}\text{C}$ koncentrációnak, mely a növényt akkor jellemezte, amikor élt. A ${}^{14}\text{C}$ szénizotóp felezési ideje 5730 év. Mikor élt a növény?  (16 pont)   Megoldás. $a)$ Az utolsó lépésben 9 liter $y$ térfogatszázalékos oldathoz adtunk 6 liter 77 térfogatszázalékos oldatot. Az $y$ számolható a következő egyenletből: $\begin{array}{c}{\displaystyle 9\cdot \frac{y}{100}+6\cdot \frac{77}{100}=15\cdot \frac{50}{100}\mathrm{.}}\end{array}$ Az egyenlet megoldása: $y=32$. Tehát a 6 liter 77 térfogatszázalékos oldatot 9 liter 32 térfogatszázalékos oldathoz adtuk hozzá. A 9 liter 32 térfogatszázalékos oldat úgy jött létre, hogy egy litert kivettünk, vagyis 10 liter 32 térfogatszázalékos oldatunk volt. Ez a 10 liter 32 térfogatszázalékos oldat keletkezett a két liternyi tiszta víz 8 liter $x$ térfogatszázalékos oldatba való visszapótlásakor. Az $x$ számolható a következő egyenletből: $\begin{array}{c}{\displaystyle 8\cdot \frac{x}{100}+2\cdot \frac{0}{100}=10\cdot \frac{32}{100}\mathrm{.}}\end{array}$ Az egyenlet megoldása: $x=40$. A nyolc liter 40 térfogatszázalékos oldat úgy keletkezett, hogy az eredeti oldatból kivettünk 2 litert, vagyis az eredeti oldat térfogatszázalékát ezzel a művelettel nem változtattuk meg, ami azt jelenti, hogy eredetileg 40 térfogatszázalékos oldat volt a hordóban. 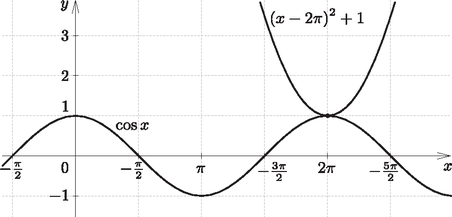$b)$ Tudjuk, hogy az egyenlet bal oldalán álló kifejezés értékkészlete: $-1\le \text{cos}x\le 1$, és tudjuk, hogy az egyenlet jobb oldalán álló kifejezés értékkészlete pedig: ${\left(x-2\pi \right)}^2+1\ge 1$. Egyenlőség csak akkor lehet, ha a két oldal ugyanazon $x$ esetén veszi fel az 1 értéket. A jobb oldal csak $x=2\pi$-nél egyenlő 1-gyel, és ekkor a bal oldal értéke is 1. Vagyis az egyenlet egyetlen megoldása: $x=2\pi$.   Megjegyzés. A grafikus megoldás is járható út.     A grafikonról leolvasható, hogy $x=2\pi$. Visszahelyettesítéssel látható, hogy ez valóban gyök. $c)$ Az $N$ értéke kifejezhető $N_0$ segítségével: $N=N_0\cdot 0\mathrm{,}65$. Az adatok behelyettesítése után: $\begin{array}{c}{\displaystyle N_0\cdot 0\mathrm{,}65=N_0\cdot {\left(\frac{1}{2}\right)}^{\frac{t}{5730}}\mathrm{.}}\end{array}$ $N_0$-val oszthatunk, majd mindkét oldal tízes alapú logaritmusát véve: $\begin{array}{c}{\displaystyle \text{lg}0\mathrm{,}65=\text{lg}{\left(\frac{1}{2}\right)}^{\frac{t}{5730}}\mathrm{.}}\end{array}$ A megfelelő azonosság alkalmazása után: $\text{lg}0\mathrm{,}65=\frac{t}{5730}\cdot \text{lg}\frac{1}{2}$. Ebből $t\approx 3561$ év adódik.   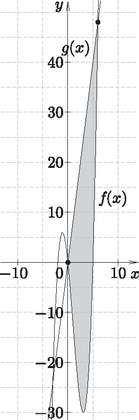6. Tekintsük az $f:\text{R}\to \text{R}$, $x\mapsto x^2\cdot \left(x-3\right)-10x$ függvényt. $a)$ Adjuk meg az $f$ függvény $-\infty$-ben és $+\infty$-ben vett határértékét. $b)$ Határozzuk meg az $f$ függvény monotonitását. $c)$ Az $f$ függvény, valamint a $g:\left[0;6\right]\to \text{R}$, $x\mapsto 8x$ függvény grafikonja által közbezárt alakzatot egy építész díszítőelemként szeretné felhasználni. Ehhez olyan koordinátarendszerben rajzolta fel a függvényeket, melyben a tengelyeken az egy egység 1 cm hosszú, és ebből az ábrából készítette el a sablont a festéshez. Hány doboz festék kell $2014$ díszítőelem felfestéséhez, ha egy doboz festék $4$ négyzetméterre elegendő?  (16 pont)   Megoldás. $a)$ Célszerű a hozzárendelési utasításban megadott kifejezést átalakítani: $\begin{array}{c}{\displaystyle x^2\cdot \left(x-3\right)-10x=x^3-3x^2-10x\mathrm{.}}\end{array}$ Az $f$ függvény $+\infty$-ben vett határértéke: $\begin{array}{c}{\displaystyle \underset{x\to +\infty }{\overset{}{\text{lim}}}\left(x^3-3x^2-10x\right)=\underset{x\to +\infty }{\overset{}{\text{lim}}}\frac{x^3-3x^2-10x}{1}=\underset{x\to +\infty }{\overset{}{\text{lim}}}{x}^3\left(1-\frac{3}{x}-\frac{10}{x^2}\right)=+\infty \mathrm{.}}\end{array}$ Az első tényező $+\infty$-hez tart, a zárójelen belüli kifejezés pedig az egyhez tart (ugyanis a $\frac{3}{x}$ és a $\frac{10}{x^2}$ a nullához tartanak), ezért a szorzat a $+\infty$-hez tart. Az $f$ függvény $-\infty$-ben vett határértéke: $\begin{array}{c}{\displaystyle \underset{x\to -\infty }{\overset{}{\text{lim}}}\left(x^3-3x^2-10x\right)=\underset{x\to -\infty }{\overset{}{\text{lim}}}\frac{x^3-3x^2-10x}{1}=\underset{x\to -\infty }{\overset{}{\text{lim}}}{x}^3\left(1-\frac{3}{x}-\frac{10}{x^2}\right)=-\infty \mathrm{.}}\end{array}$ Az első tényező $-\infty$-hez tart, a zárójelen belüli kifejezés pedig az egyhez tart, ezért a szorzat a $-\infty$-hez tart. $b)$ A függvény növekedési és fogyási viszonyaira az első deriváltból lehet következtetni: $\begin{array}{c}{\displaystyle \left[x^3-3x^2-10x\right]\text{'}=3x^2-6x-10.}\end{array}$ Az első derivált zérushelyei a $3x^2-6x-10=0$ egyenlet megoldásai: $x_{\mathrm{1,2}}=1\pm \sqrt[]{\frac{13}{3}}$.   ${\displaystyle \begin{array}{|cccccc|}\hline \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false"><</mo><mn>1</mn><mo stretchy="false">-</mo><mrow><mroot><mrow><mrow><mfrac><mrow><mn>13</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></mrow><mrow></mrow></mroot></mrow></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">=</mo><mn>1</mn><mo stretchy="false">-</mo><mrow><mroot><mrow><mrow><mfrac><mrow><mn>13</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></mrow><mrow></mrow></mroot></mrow></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1</mn><mo stretchy="false">-</mo><mrow><mroot><mrow><mrow><mfrac><mrow><mn>13</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></mrow><mrow></mrow></mroot></mrow><mo stretchy="false"><</mo><mi>x</mi><mo stretchy="false"><</mo></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">=</mo><mn>1</mn><mo stretchy="false">+</mo><mrow><mroot><mrow><mrow><mfrac><mrow><mn>13</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></mrow><mrow></mrow></mroot></mrow></math> }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1</mn><mo stretchy="false">+</mo><mrow><mroot><mrow><mrow><mfrac><mrow><mn>13</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></mrow><mrow></mrow></mroot></mrow><mo stretchy="false"><</mo><mi>x</mi></math> }}\hfill \\ \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false"><</mo><mn>1</mn><mo stretchy="false">+</mo><mrow><mroot><mrow><mrow><mfrac><mrow><mn>13</mn></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></mrow><mrow></mrow></mroot></mrow></math>}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mo stretchy="false">'</mo><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>x</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">+</mo></math>}}\hfill & \hfill {\displaystyle \text{ 0}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo></math>}}\hfill & \hfill {\displaystyle \text{ 0}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">+</mo></math> }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>x</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>}}\hfill & \hfill {\displaystyle \text{ növekedő}}\hfill & \hfill {\displaystyle \text{ lokális maximum}}\hfill & \hfill {\displaystyle \text{ fogyó}}\hfill & \hfill {\displaystyle \text{ lokális minimum}}\hfill & \hfill {\displaystyle \text{ növekedő }}\hfill \\ \hline\end{array}}$   $c)$ Az $f\left(x\right)=x^2\cdot \left(x-3\right)-10x$ függvény és az $x\in \left[0;6\right]$ intervallumon értelmezett $g\left(x\right)=8x$ függvény metszéspontjai az $x^3-3x^2-10x=8x$ egyenletből kaphatók. Átrendezve az egyenletet, és $x$-et kiemelve adódik: $x\cdot \left(x^2-3x-18\right)=0$. Ennek megoldásai az adott intervallumon: $x_1=0$; $x_2=6$ ($x_3=-3$ nincs az adott intervallumban), ezért az $f\left(x\right)$ és a $g\left(x\right)$ függvények $x\in \left[0;6\right]$ intervallumra eső görbéi által meghatározott zárt terület nagyságát kell kiszámolnunk. A keresett terület: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle \underset{0}{\overset{6}{\int }}\left(g\left(x\right)-f\left(x\right)\right)dx=\underset{0}{\overset{6}{\int }}\left(8x-\left(x^3-3x^2-10x\right)\right)dx=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\underset{0}{\overset{6}{\int }}\left(-x^3+3x^2+18x\right)dx=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={\left[-\frac{x^4}{4}+x^3+9x^2\right]}_0^6=-\frac{6^4}{4}+216+324=216\left({\text{cm}}^2\right)\mathrm{.}}\hfill \end{array}}$ 2014 darab ilyen motívum összterülete: $\begin{array}{c}{\displaystyle 2014\cdot 216\text{c<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}=435024{\text{cm}}^2=43\mathrm{,}5024{\text{m}}^2\mathrm{.}}\end{array}$     Lefestésükhöz 11 doboz festék szükséges.   7. $a)$ Adjuk meg a következő állítások megfordítását. Döntsük el az eredeti állításokról és a megfordításaikról, hogy melyik igaz, melyik hamis. $1.$ Ha egy háromszögnek van két hegyesszöge, akkor van egy tompaszöge. $2.$ Ha két vektor tompaszöget zár be egymással, akkor skaláris szorzatuk negatív. $3.$ Ha egy függvénynek egy adott $x_0$ pontbeli deriváltja $0$, akkor a függvénynek az adott $x_0$ helyen szélsőértéke van. $4.$ Ha egy sokszög szabályos, akkor középpontosan szimmetrikus. $5.$ Ha egy négyszög középpontosan szimmetrikus, akkor paralelogramma. $b)$ Fogalmazzuk meg az $5.$ állítást és megfordítását egyetlen mondatban. $c)$ Egy kalapban golyók, játékkockák és papírkorongok vannak. A következőket tudjuk biztosan: ‐ A kalapban golyóból is, játékkockából is és papírkorongból is van legalább kettő. ‐ A tárgyak színe különböző is lehet, de mindegyik tárgy színe egyértelmű. ‐ A kalapban minden golyó lila. ‐ A kalapban nincs lila játékkocka. Egy robot véletlenszerűen kiválaszt egy tárgyat a kalapból, de ezt nem mutatja meg nekünk. Döntsük el melyik állítás igaz és melyik hamis a következők közül. Indokoljuk válaszainkat. I. Ha a kalapból kiválasztott tárgy nem golyó, akkor biztosan nem lila. II. Ha a kalapból kiválasztott tárgy nem lila, akkor biztosan nem golyó. III. Ha a kalapból kiválasztott tárgy nem lila, akkor biztosan játékkocka. IV. Ha a kalapból kiválasztott tárgy nem játékkocka, akkor biztosan lila. $d)$ A szünetben gyerekek szaladgálnak az iskola udvarán, megszámolni őket képtelenség. Semmit nem tudunk ezekről a gyerekekről, de azt az egy információt megkaptuk, hogy van köztük $54$ fő, akiknek azonos hónapban van a születésnapjuk. I. Legalább hány gyerek van az udvaron? II. Mennyinek kell lennie egy számunkra ismeretlen születési adatokkal rendelkező, tetszőlegesen kiválasztott gyerekekből álló csoport létszámának, hogy biztonsággal állíthassuk, hogy van köztük $20$ fő, akiknek ugyanabban a hónapban van a születésnapjuk?  (16 pont)   Megoldás. $a)$ Az állítások megfordítása: 1. Ha egy háromszögnek van egy tompaszöge, akkor van két hegyesszöge. 2. Ha két vektor skaláris szorzata negatív, akkor tompaszöget zárnak be egymással. 3. Ha egy függvénynek egy adott $x_0$ helyen szélsőértéke van, akkor a függvény adott$x_0$ pontbeli deriváltja 0. 4. Ha egy sokszög középpontosan szimmetrikus, akkor szabályos. 5. Ha egy négyszög paralelogramma, akkor középpontosan szimmetrikus.   ${\displaystyle \begin{array}{|ccc|}\hline {\displaystyle }\hfill & \hfill {\displaystyle \text{ Állítás}}\hfill & \hfill {\displaystyle \text{ Megfordítása }}\hfill \\ {\displaystyle \text{1. állítás}}\hfill & \hfill {\displaystyle \text{ hamis}}\hfill & \hfill {\displaystyle \text{ igaz }}\hfill \\ {\displaystyle \text{2. állítás}}\hfill & \hfill {\displaystyle \text{ igaz}}\hfill & \hfill {\displaystyle \text{ hamis }}\hfill \\ {\displaystyle \text{3. állítás}}\hfill & \hfill {\displaystyle \text{ hamis}}\hfill & \hfill {\displaystyle \text{ igaz }}\hfill \\ {\displaystyle \text{4. állítás}}\hfill & \hfill {\displaystyle \text{ hamis}}\hfill & \hfill {\displaystyle \text{ hamis }}\hfill \\ {\displaystyle \text{5. állítás}}\hfill & \hfill {\displaystyle \text{ igaz}}\hfill & \hfill {\displaystyle \text{ igaz }}\hfill \\ \hline\end{array}}$   $b)$ Egy négyszög akkor és csak akkor paralelogramma, ha középpontosan szimmetrikus. $c)$ Az I. állítás hamis, mert lehet, hogy papírkorongot választott a robot, azok között pedig lehet lila. A II. állítás igaz, mert annak, hogy golyó legyen, szükséges feltétele, hogy lila is legyen. A III. állítás hamis, mert ha a kiválasztott tárgy nem lila, akkor az akár papírkorong is lehet. A IV. állítás hamis, mert ha a tárgy nem játékkocka, akkor nemcsak golyó lehet, hanem papírkorong is, ami viszont nem feltétlenül lila. $d)$ I. Nyilvánvaló, hogy legalább 54-en kell, hogy legyenek. II. A skatulya elvet felhasználva $12\cdot 19+1=229$ számú gyerekről teljes biztonsággal állíthatjuk, hogy van köztük 20 fő, akiknek ugyanabban a hónapban van a születésnapja.   8. Egy cipőbolt vásárlói közül $60$ felnőtt férfit kérdeztünk meg a lábméretéről. Az így kapott adatokat az alábbi táblázatban rögzítettük.   ${\displaystyle \begin{array}{|cccccccccc|}\hline \hfill {\displaystyle \text{39}}\hfill & \hfill {\displaystyle \text{44}}\hfill & \hfill {\displaystyle \text{42}}\hfill & \hfill {\displaystyle \text{40}}\hfill & \hfill {\displaystyle \text{45}}\hfill & \hfill {\displaystyle \text{43}}\hfill & \hfill {\displaystyle \text{40}}\hfill & \hfill {\displaystyle \text{42}}\hfill & \hfill {\displaystyle \text{45}}\hfill & \hfill {\displaystyle \text{43 }}\hfill \\ \hfill {\displaystyle \text{43}}\hfill & \hfill {\displaystyle \text{41}}\hfill & \hfill {\displaystyle \text{45}}\hfill & \hfill {\displaystyle \text{41}}\hfill & \hfill {\displaystyle \text{46}}\hfill & \hfill {\displaystyle \text{43}}\hfill & \hfill {\displaystyle \text{44}}\hfill & \hfill {\displaystyle \text{43}}\hfill & \hfill {\displaystyle \text{48}}\hfill & \hfill {\displaystyle \text{45 }}\hfill \\ \hfill {\displaystyle \text{46}}\hfill & \hfill {\displaystyle \text{42}}\hfill & \hfill {\displaystyle \text{44}}\hfill & \hfill {\displaystyle \text{47}}\hfill & \hfill {\displaystyle \text{38}}\hfill & \hfill {\displaystyle \text{42}}\hfill & \hfill {\displaystyle \text{45}}\hfill & \hfill {\displaystyle \text{44}}\hfill & \hfill {\displaystyle \text{44}}\hfill & \hfill {\displaystyle \text{39 }}\hfill \\ \hfill {\displaystyle \text{40}}\hfill & \hfill {\displaystyle \text{46}}\hfill & \hfill {\displaystyle \text{43}}\hfill & \hfill {\displaystyle \text{41}}\hfill & \hfill {\displaystyle \text{45}}\hfill & \hfill {\displaystyle \text{46}}\hfill & \hfill {\displaystyle \text{45}}\hfill & \hfill {\displaystyle \text{40}}\hfill & \hfill {\displaystyle \text{43}}\hfill & \hfill {\displaystyle \text{44 }}\hfill \\ \hfill {\displaystyle \text{45}}\hfill & \hfill {\displaystyle \text{43}}\hfill & \hfill {\displaystyle \text{46}}\hfill & \hfill {\displaystyle \text{44}}\hfill & \hfill {\displaystyle \text{42}}\hfill & \hfill {\displaystyle \text{43}}\hfill & \hfill {\displaystyle \text{41}}\hfill & \hfill {\displaystyle \text{45}}\hfill & \hfill {\displaystyle \text{42}}\hfill & \hfill {\displaystyle \text{40 }}\hfill \\ \hfill {\displaystyle \text{44}}\hfill & \hfill {\displaystyle \text{42}}\hfill & \hfill {\displaystyle \text{41}}\hfill & \hfill {\displaystyle \text{45}}\hfill & \hfill {\displaystyle \text{42}}\hfill & \hfill {\displaystyle \text{44}}\hfill & \hfill {\displaystyle \text{45}}\hfill & \hfill {\displaystyle \text{41}}\hfill & \hfill {\displaystyle \text{44}}\hfill & \hfill {\displaystyle \text{45 }}\hfill \\ \hline\end{array}}$   $a)$ Határozzuk meg az egyes cipőméretek gyakoriságát és relatív gyakoriságát. Az eredményeket foglaljuk táblázatba. 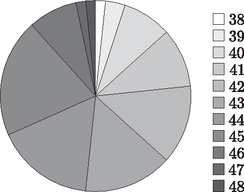$b)$ Készítsünk kördiagramot az egyes cipőméretek előfordulási számáról. $c)$ Határozzuk meg a $60$ felnőtt férfi átlagos cipőméretét, és számoljuk ki a cipőméretek szórását. $d)$ Mennyi a cipőméretek módusza, mediánja és terjedelme?  (16 pont)   Megoldás. $a)$     $b)$        $c)$ A cipőméretek átlaga: $\begin{array}{c}{\displaystyle \frac{38+2\cdot 39+5\cdot 40+6\cdot 41+8\cdot 42+9\cdot 43+10\cdot 44+12\cdot 45+5\cdot 46+47+48}{60}\approx \mathrm{43,17.}}\end{array}$ A cipőméretek szórása: $\begin{array}{c}{\displaystyle \sqrt[]{\frac{{\left(43\mathrm{,}17-38\right)}^2+2{\left(43\mathrm{,}17-39\right)}^2+\text{...}+{\left(43\mathrm{,}17-47\right)}^2+{\left(43\mathrm{,}17-48\right)}^2}{60}}\approx 2\mathrm{,}15.}\end{array}$ $d)$ A cipőméretek módusza: 45, mediánja: 43, terjedelme: 10.   9. $a)$ Felírtunk egy papírra $5$ számot. Az első három szám egy számtani sorozat három egymást követő eleme. A harmadik, a negyedik és az ötödik szám szintén egy számtani sorozat három egymást követő eleme. Az első, a harmadik és a negyedik szám szintén egy számtani sorozat egymást követő elemei. A második, a harmadik és a negyedik szám egy mértani sorozat három egymást követő eleme. A számok összege $26$. Melyik ez az öt szám? $b)$ Összeadtuk a $2^1$; $2^2$; $2^3$; $\text{...}$; $2^{99}$; $2^{100}$ hatványok $x$ alapú logaritmusát és $10100$-at kaptunk. Mennyi az $x$ értéke?  (16 pont)   Megoldás. $a)$ Legyen az öt szám: $x_1$, $x_2$, $x_3$, $x_4$, $x_5$. A feladat szövege alapján a következő egyenletrendszer írható fel: $\begin{array}{c}{\displaystyle \{{\displaystyle \begin{array}{cc}\hfill {\displaystyle x_2-x_1}& {\displaystyle =x_3-x_2\mathrm{,}}\hfill \\ \hfill {\displaystyle x_4-x_3}& {\displaystyle =x_5-x_4\mathrm{,}}\hfill \\ \hfill {\displaystyle x_3-x_1}& {\displaystyle =x_4-x_3\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{x_3}{x_2}}& {\displaystyle =\frac{x_4}{x_3}\mathrm{,}}\hfill \\ \hfill {\displaystyle x_1+x_2+x_3}& {\displaystyle +x_4+x_5=26.}\hfill \end{array}}}\end{array}$ Az egyenletrendszert az ismeretlenek fokozatos kiküszöbölésének módszerével oldjuk meg. Az első egyenletből kapjuk, hogy $x_1=2x_2-x_3$, ezt behelyettesítve a harmadik és az utolsó egyenletbe, négy egyenletünk marad: $\begin{array}{c}{\displaystyle \{{\displaystyle \begin{array}{cc}\hfill {\displaystyle x_4-x_3}& {\displaystyle =x_5-x_4\mathrm{,}}\hfill \\ \hfill {\displaystyle x_3-\left(2x_2-x_3\right)}& {\displaystyle =x_4-x_3\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{x_3}{x_2}}& {\displaystyle =\frac{x_4}{x_3}\mathrm{,}}\hfill \\ \hfill {\displaystyle \left(2x_2-x_3\right)+x_2}& {\displaystyle +x_3+x_4+x_5=26.}\hfill \end{array}}}\end{array}$ Néhány egyenlet átrendezése után kapjuk: $\begin{array}{c}{\displaystyle \{{\displaystyle \begin{array}{cc}\hfill {\displaystyle 2x_4-x_3}& {\displaystyle =x_5\mathrm{,}}\hfill \\ \hfill {\displaystyle {3x}_3-2x_2}& {\displaystyle =x_4\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{x_3}{x_2}}& {\displaystyle =\frac{x_4}{x_3}\mathrm{,}}\hfill \\ \hfill {\displaystyle 3x_2+x_4}& {\displaystyle +x_5=26.}\hfill \end{array}}}\end{array}$ Az $x_5=2x_4-x_3$ kifejezést behelyettesítve az utolsó egyenletbe: $\begin{array}{c}{\displaystyle \{{\displaystyle \begin{array}{cc}\hfill {\displaystyle {3x}_3-2x_2}& {\displaystyle =x_4\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{x_3}{x_2}}& {\displaystyle =\frac{x_4}{x_3}\mathrm{,}}\hfill \\ \hfill {\displaystyle 3x_2+x_4}& {\displaystyle +\left(2x_4-x_3\right)=26.}\hfill \end{array}}}\end{array}$ Az utolsó egyenlet rendezése és az $x_4=3x_3-2x_2$ behelyettesítése után: $\begin{array}{c}{\displaystyle \{{\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{x_3}{x_2}=\frac{{3x}_3-2x_2}{x_3}\mathrm{,}}\hfill \\ \hfill {\displaystyle 3x_2-x_3+3\left({3x}_3-2x_2\right)=26.}\hfill \end{array}}}\end{array}$ A második egyenletből kifejezett $x_2=\frac{8x_3-26}{3}$ érték behelyettesítése után másodfokú egyenletet kapunk: $\begin{array}{c}{\displaystyle x_3^2=3\cdot \frac{8x_3-26}{3}{x}_3-2{\left(\frac{8x_3-26}{3}\right)}^2\mathrm{.}}\end{array}$ Az egyenlet nullára redukált alakja: $5x_3^2-46x_3+104=0$. A megoldóképlet alkalmazása után $x_3$-ra két érték adódik: $x_{3_1}=4$; $x_{3_2}=5\mathrm{,}2$. Elvégezve a megfelelő visszahelyettesítéseket a következő két megoldást kapjuk: 1. $x_1=x_2=x_3=x_4=x_5=5\mathrm{,}2$. 2. $x_1=0$; $x_2=2$; $x_3=4$; $x_4=8$; $x_5=12$. $b)$ A feladat feltételei alapján a következő egyenlet írható fel: $\begin{array}{c}{\displaystyle \text{log}{}_x{2}^1+\text{log}{}_x{2}^2+\text{log}{}_x{2}^3+\text{...}+\text{log}{}_x{2}^{99}+\text{log}{}_x{2}^{100}=10\mathrm{100,}\text{ahol }x>0;x\ne 1.}\end{array}$ A megfelelő azonosságot alkalmazva kapjuk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{log}{}_x\left(2^1\cdot 2^2\cdot 2^3\cdot \text{...}\cdot 2^{99}\cdot 2^{100}\right)}& {\displaystyle =10\mathrm{100,}}\hfill \\ \hfill {\displaystyle \text{log}{}_x\left(2^{\frac{\left(100+1\right)100}{2}}\right)}& {\displaystyle =10\mathrm{100,}}\hfill \\ \hfill {\displaystyle \text{log}{}_x{2}^{5050}}& {\displaystyle =10\mathrm{100,}}\hfill \\ \hfill {\displaystyle 5050\cdot \text{log}{}_{x}2}& {\displaystyle =10\mathrm{100,}}\hfill \\ \hfill {\displaystyle \text{log}{}_{x}2}& {\displaystyle =2.}\hfill \end{array}}$ A logaritmus definíciója miatt az egyedüli megoldás: $x=\sqrt[]{2}$.