Cím:	Megoldásvázlatok a 2013/9. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Számadó László
Füzet:	2014/január, 10 - 17. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldásvázlatok a 2013/9. sz. emelt szintű gyakorló feladataihoz   I. rész     1. Egy televíziós tehetségkutató műsorban négy mentor énekesei versenyeznek. A nézők telefonos szavazatai alapján alakul ki a sorrend. A műsorvezető az izgalom fokozása miatt minden mentornak ad egy kis információt a szavazás állásáról. Sorban ezek az állítások hangzottak el: A három versenyződ közül pontosan kettő nincs az utolsó három hely egyikén. A két versenyződ közül pontosan egy áll az utolsó három hely egyikén. A két versenyződ közül legalább egy az utolsó három hely egyikén áll. A két versenyződ közül legalább egy biztosan nincs az utolsó három hely egyikén. $a)$ A négy mentor közül gondolhatja-e ekkor valamelyik azt, hogy a versenyzői közül semelyik sincs az utolsó három hely egyikén? $b)$ Hányféle sorrend képzelhető el az elhangzott mondatok alapján?  (11 pont)   Megoldás. $a)$ Az elhangzottak alapján az első mentornak pontosan egy versenyzője az utolsó három hely valamelyikén áll. Hasonlóan a második mentornak is pontosan egy versenyzője áll az utolsó három hely valamelyikén. A harmadik mentor egy vagy kettő versenyzője lehet ezeken a helyeken, de az eddigiek alapján tudható, hogy már csak egy ilyen versenyző lehet. Mindezeket figyelembe véve a negyedik mentor két versenyzője közül ,,a legalább egy biztosan nincs az utolsó három hely egyikén'' úgy valósulhat meg, hogy egyik sincs az utolsó három hely egyikén. Vagyis a negyedik mentor nyugodt lehet, mert az utolsó három hely egyikén sincs versenyzője. $b)$ Legyen az első mentor három versenyzője: $A_1$, $A_2$, $A_3$, a második mentoré: $B_1$, $B_2$, a harmadik mentoré: $C_1$, $C_2$, a negyedik mentoré pedig: $D_1$, $D_2$. Ezt a kilenc versenyzőt kell a megfelelő információk alapján az összes lehetséges módon sorba rendezve elképzelnünk. Tudjuk, hogy az első, második és harmadik mentor egy-egy versenyzője az utolsó három hely valamelyikén áll (például az $A_1$, $B_1$, $C_1$ versenyzők). A további hat versenyző ezeket $6!$-féle sorrendben előzheti meg. A három versenyző pedig $3!$-féle sorrendben állhat az utolsó három helyen. Ez $6!\cdot 3!=4320$ eset. A három gyengén szereplő kiválasztására is több lehetőségünk van. Összesen $3\cdot 2\cdot 2=12$-féleképpen képzelhető az utolsó három helyen végzettek kiválasztása. Vagyis az összes elképzelhető sorrendek száma: $12\cdot 4320=51840$.   2. Oldjuk meg a következő egyenletet: $\begin{array}{c}{\displaystyle \text{lg}\left(2-x\right)\cdot \sqrt[]{6-x-x^2}\cdot \text{sin}\left(x-\frac{\pi }{6}\right)=0.}\end{array}$ (12 pont)   Megoldás. A logaritmus miatt: $2-x>0$. Ezek szerint: $x\in \left]-\infty ;2\right[$. A négyzetgyök miatt: $6-x-x^2\ge 0$, azaz $\left(2-x\right)\left(x+3\right)\ge 0$. Ezek szerint: $x\in \left[-3;2\right]$. Vagyis a feladat értelmezési tartománya: $x\in \left[-3;2\right[$. A három tényező zérushelyeit külön-külön megvizsgáljuk. Az első tényező zérushelye az 1, és ez benne van a feladat értelmezési tartományában. A második tényező zérushelyei a $-3$ és a 2. Ebből csak a $-3$ van benne a feladat értelmezési tartományában. A harmadik tényező zérushelyei a $\frac{\pi }{6}+k\pi$, ahol $k$ egész szám. A feladat értelmezési tartománya miatt csak a $k=-1$ és a $k=0$ ad megfelelő értéket. 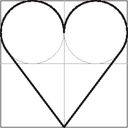Ezek alapján a feladat megoldásai: $\begin{array}{c}{\displaystyle -\mathrm{3,}-\frac{5\pi }{6}\mathrm{,}\frac{\pi }{6}\mathrm{,}1.}\end{array}$     3. Enikő pólóján egy olyan szív alakú forma látható, amelyet egy 24 cm oldalú négyzetbe lehet rajzolni az ábrán látható módon. Mekkora az így kapott szív kerülete, területe?  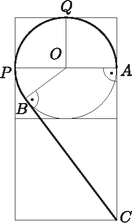(14 pont)       Megoldás. Az ábra függőlegesen szimmetrikus, ezért elég a felével foglalkoznunk. A körök sugara a nagy négyzet oldalának negyedével egyenlő hosszú, azaz 6 cm. Adott körhöz külső pontból két azonos hosszúságú érintőszakasz húzható, ezért $CA=CB$. A $CA$ pedig a nagy négyzet oldalának háromnegyedével egyenlő. Vagyis $CA=$ =CB=18 cm. Ezek alapján a $CAOB$ derékszögű deltoid területe: $\begin{array}{c}{\displaystyle T_1=6\cdot 18=108{\text{(cm}}^2)\mathrm{.}}\end{array}$ Az $OBC$ derékszögű háromszögben   az $O$-nál lévő $\alpha$ hegyesszögre: $\text{tg}\alpha =\frac{18}{6}=3$, vagyis $2\alpha \approx 143\mathrm{,}{13}^{\circ }$.     A ${360}^{\circ }-143\mathrm{,}{13}^{\circ }=216\mathrm{,}{87}^{\circ }$-os $AB$ körívhez tartozó körcikk területe: $\begin{array}{c}{\displaystyle T_2=6^2\cdot \pi \cdot \frac{216\mathrm{,}{87}^{\circ }}{{360}^{\circ }}\approx 68\mathrm{,}13{\text{(cm}}^2)\mathrm{.}}\end{array}$ A szív alakú forma területe: $\begin{array}{c}{\displaystyle 2\left(T_1+T_2\right)=2\left(108+68\mathrm{,}13\right)=352\mathrm{,}26{\text{(cm}}^2)\mathrm{.}}\end{array}$ A ${360}^{\circ }-143\mathrm{,}{13}^{\circ }=216\mathrm{,}{87}^{\circ }$-os $AB$ körív hossza: $\begin{array}{c}{\displaystyle I=2\cdot 6\cdot \pi \cdot \frac{216\mathrm{,}{87}^{\circ }}{{360}^{\circ }}\approx 22\mathrm{,}71\text{(cm). }}\end{array}$ A szív alakú forma kerülete: $\begin{array}{c}{\displaystyle K=2\left(I+BC\right)=2\left(22\mathrm{,}71+18\right)=81\mathrm{,}42\text{(cm). }}\end{array}$   4. Kiválasztottunk nyolc olyan várost, amelyek közül bármelyik kettő között közvetlen repülőgép összeköttetés van. Egy téli napon a rendkívüli időjárási viszonyok miatt az összes ilyen útvonalból kilencen szüneteltetik a közlekedést. Mennyi annak a valószínűsége, hogy négy véletlenszerűen választott útvonalból pontosan kettőn van közlekedés?  (14 pont)   Megoldás.   Mivel bármelyik kettő között közvetlen repülőgép összeköttetés van, ezért a nyolc város között összesen $\left(\genfrac{}{}{0ex}{}{8}{2}\right)$, azaz 28 útvonal van.   Összeszámoljuk az összes lehetőségek számát. A 28 útvonal közül négyet választunk véletlenszerűen. Ezt $\left(\genfrac{}{}{0ex}{}{28}{4}\right)$-féleképpen tehetjük meg. Most a vizsgált esemény szempontjából a kedvező eseteket számoljuk össze. A két útvonalat, amelyen nincs közlekedés kilencből választhatjuk, a két útvonalat, amelyen pedig van közlekedés, 19-ből választhatjuk. Vagyis ezek száma összesen: $\left(\genfrac{}{}{0ex}{}{9}{2}\right)\left(\genfrac{}{}{0ex}{}{19}{2}\right)$. A keresett valószínűséget a kedvező esetek számának és az összes esetek számának hányadosa adja: $\begin{array}{c}{\displaystyle p=\frac{\left(\genfrac{}{}{0ex}{}{9}{2}\right)\left(\genfrac{}{}{0ex}{}{19}{2}\right)}{\left(\genfrac{}{}{0ex}{}{28}{4}\right)}\approx 0\mathrm{,}3.}\end{array}$   II. rész     5. Oldjuk meg a valós számok halmazán a következő egyenletet: $\begin{array}{c}{\displaystyle {\left(\frac{\sqrt[]{5}}{4}\right)}^{\frac{12-2\text{lg}x}{-5+\text{lg}x}-\frac{4}{1+\text{lg}x}}=10\mathrm{,}24.}\end{array}$ (16 pont)   Megoldás. Csak pozitív számnak van logaritmusa, ezért $x>0$, továbbá a nevezők nem lehetnek 0-val egyenlők, ezért $x\ne {10}^5$, valamint $x\ne {10}^{-1}$. Vagyis a feladat értelmezési tartománya: ${\text{R}}^{+}\setminus \left\{{10}^{-1};{10}^5\right\}$. Mivel $\begin{array}{c}{\displaystyle 10\mathrm{,}24=\frac{1024}{100}=\frac{256}{25}=\frac{4^4}{{\sqrt[]{5}}^4}={\left(\frac{\sqrt[]{5}}{4}\right)}^{-4}\mathrm{,}}\end{array}$ azért az eredeti egyenletünk így írható: $\begin{array}{c}{\displaystyle {\left(\frac{\sqrt[]{5}}{4}\right)}^{\frac{12-2\text{lg}x}{-5+\text{lg}x}-\frac{4}{1+\text{lg}x}}={\left(\frac{\sqrt[]{5}}{4}\right)}^{-4}\mathrm{.}}\end{array}$ Az exponenciális függvény kölcsönös egyértelműsége alapján kapjuk, hogy: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{12-2\text{lg}x}{-5+\text{lg}x}-\frac{4}{1+\text{lg}x}=-\mathrm{4,}}\hfill \\ \hfill {\displaystyle \left(12-2\text{lg}x\right)\left(1+\text{lg}x\right)-4\left(-5+\text{lg}x\right)=-4\left(-5+\text{lg}x\right)\left(1+\text{lg}x\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{lg}{}^{2}x-5\text{lg}x+6=0.}\hfill \end{array}}$ Ez $\text{lg}x$-re másodfokú, az egyenlet két megoldása: $\text{lg}{x}_1=2$, $\text{lg}{x}_2=3$. Vagyis: $x_1=100$, $x_2=1000$. Ezek benne vannak az értelmezési tartományban, valóban megoldásai az egyenletnek.   6. 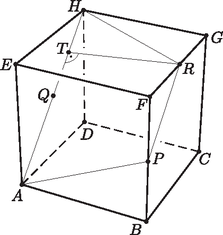Az $ABCDEFGH$ kockát kettévágtuk az $A$ csúcsra, a $BF$ él $P$ felezőpontjára és az $ADHE$ oldallap $Q$ középpontjára illeszkedő síkkal. $a)$ Mekkora a vágásfelület területe a kocka élével kifejezve? $b)$ Hogyan aránylik egymáshoz a kocka két részének térfogata?  (16 pont)   Megoldás. $a)$ A vágás síkjában lévő $AQ$ egyenesre illeszkedik a $H$ pont, ezért $H$ is rajta van a vágásfelületen. Az $ADHE$ és $BCGF$ párhuzamos lapjai a kockának, ezért a vágási síkkal alkotott metszésvonaluk párhuzamos egymással. Az egyik metszésvonal az $AH$ egyenes, a vele párhuzamos $P$ ponton áthaladó metszésvonal az $FG$ élt az $R$ felezőpontban metszi. Vagyis az $APRH$ síkidom (ami egy húrtrapéz) a vágásfelület, ennek a területét kell meghatároznunk. Az $AH=a\sqrt[]{2}$, mert az $a$ oldalú négyzet átlójáról van szó. A $PR=a\frac{\sqrt[]{2}}{2}$, mert ez a szakasz az $a$ oldalú négyzet átlójának felével egyenlő hosszúságú. A $HR=AP$ szárak hosszát meghatározhatjuk a $HGR$ derékszögű háromszögben Pitagorasz-tétel segítségével: $\begin{array}{c}{\displaystyle HR=\sqrt[]{a^2+{\left(\frac{a}{2}\right)}^2}=a\frac{\sqrt[]{5}}{2}\mathrm{.}}\end{array}$ A vágás síkjában lévő $RTH$ derékszögű háromszögben $\begin{array}{c}{\displaystyle TH=\frac{AH-PR}{2}=a\frac{\sqrt[]{2}}{4}\mathrm{.}}\end{array}$     Pitagorasz-tétel alkalmazásával megkapjuk az $APRH$ trapéz $TR$ magasságát: $\begin{array}{c}{\displaystyle TR=\sqrt[]{{HR}^2-{TH}^2}=\sqrt[]{\frac{5}{4}{a}^2-\frac{1}{8}{a}^2}=a\frac{3}{2\sqrt[]{2}}=a\frac{3\sqrt[]{2}}{4}\mathrm{.}}\end{array}$ A vágásfelület területe: $\begin{array}{c}{\displaystyle T=\frac{(a\sqrt[]{2}+a\frac{\sqrt[]{2}}{2})\cdot a\frac{3\sqrt[]{2}}{4}}{2}=\frac{9}{8}{a}^2\mathrm{.}}\end{array}$ $b)$ Az egyik rész egy $AEH$ (egyenlő szárú, derékszögű háromszög) alaplapú és $PFR$ fedőlapú csonkagúla. Alaplapjának területe: $T=\frac{a\cdot a}{2}=\frac{a^2}{2}$, fedőlapjának területe: $\begin{array}{c}{\displaystyle t=\frac{\frac{a}{2}\cdot \frac{a}{2}}{2}=\frac{a^2}{8}\mathrm{.}}\end{array}$ A két sík távolsága $a$, ez adja a csonkagúla $m$ magasságát. Most már alkalmazhatjuk a csonkagúla térfogatképletét: $\begin{array}{c}{\displaystyle V_1=\frac{m}{3}\left(T+\sqrt[]{Tt}+t\right)=\frac{a}{3}\left(\frac{a^2}{2}+\sqrt[]{\frac{a^2}{2}\cdot \frac{a^2}{8}}+\frac{a^2}{8}\right)=\frac{a}{3}\cdot \frac{7a^2}{8}=\frac{7}{24}{a}^3\mathrm{.}}\end{array}$ A másik rész térfogata: $\begin{array}{c}{\displaystyle V_2=a^3-\frac{7}{24}{a}^3=\frac{17}{24}{a}^3\mathrm{.}}\end{array}$ Tehát a két rész aránya: $\begin{array}{c}{\displaystyle \frac{V_1}{V_2}=\frac{\frac{7}{24}{a}^3}{\frac{17}{24}{a}^3}=\frac{7}{17}\mathrm{.}}\end{array}$     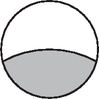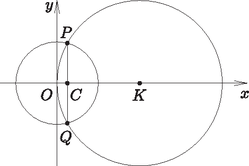7. Az ábrán Ibolya egyik fülbevalójának vázlatrajza látható. A körlemez középpontján áthaladó körív sugara kétszerese az eredeti körlemez sugarának. A fülbevaló hány százaléka sötétebb árnyalatú?  (16 pont)       Megoldás. Nem megy az általánosság rovására, ha a fülbevaló sugarát 1-nek, a benne lévő körív sugarát pedig 2-nek vesszük. Helyezzük az ábrát koordinátarendszerbe olyan módon, hogy a kör $O$ középpontja az origó, a körív középpontja a $K\left(2;0\right)$ koordinátájú pont legyen. Ekkor a két kör egyenlete: $\begin{array}{c}{\displaystyle x^2+y^2=\mathrm{1,}{\left(x-2\right)}^2+y^2=4.}\end{array}$     Meg szeretnénk határozni a két kör metszéspontjainak koordinátáit, ezért megoldjuk az egyenletrendszert. A második egyenletben a négyzetre emelés elvégzése után az $x^2+y^2$ helyére 1-et írhatunk: $\begin{array}{c}{\displaystyle -4x+4+1=\mathrm{4,}x=\frac{1}{4}\mathrm{.}}\end{array}$ Ezt visszahelyettesítve például az első egyenletbe, kapjuk a két metszéspont koordinátáit: $\begin{array}{c}{\displaystyle P\left(\frac{1}{4};\frac{\sqrt[]{15}}{4}\right)\mathrm{,}Q\left(\frac{1}{4};-\frac{\sqrt[]{15}}{4}\right)\mathrm{.}}\end{array}$ A fülbevaló sötétebb részét a $PQ$ szakasz két körszeletre vágja. Ezeknek megadjuk külön-külön a területét. Alkalmazzuk a körszelet területképletét: $T=\frac{1}{2}\left[ri-h\left(r-m\right)\right]$, ahol $r$ a körív sugara, $i$ a körív hossza, $h$ a határoló húr hossza, $m$ pedig a körszelet magassága. Az 1 sugarú körszelet területéhez már a következő adatok a rendelkezésünkre állnak: $\begin{array}{c}{\displaystyle r_1=\mathrm{1,}{h}_1=PQ=2\cdot \frac{\sqrt[]{15}}{4}=\frac{\sqrt[]{15}}{2}\mathrm{,}{m}_1=\frac{3}{4}\mathrm{.}}\end{array}$ Meg kell még adnunk a megfelelő $PQ$ körív hosszát. Ehhez a $POQ$ nagyságát kell ismernünk. A $POC$ derékszögű háromszögben (ahol a $PQ$ és a vízszintes tengely metszéspontja a $C$ pont) az $O$-nál lévő $\beta$ szögre: $\begin{array}{c}{\displaystyle \text{tg}\beta =\frac{\frac{\sqrt[]{15}}{4}}{\frac{1}{4}}=\sqrt[]{15}\mathrm{,}}\end{array}$ ahonnan $POQ=2\beta \approx 151\mathrm{,}{04}^{\circ }$. Vagyis $\begin{array}{c}{\displaystyle \frac{i_1}{2\pi }=\frac{151\mathrm{,}{04}^{\circ }}{{360}^{\circ }}\mathrm{,}\text{azaz}{i}_1\approx 2\mathrm{,}636.}\end{array}$ Behelyettesítünk a területképletbe: $\begin{array}{c}{\displaystyle T_1=\frac{1}{2}\left[1\cdot 2\mathrm{,}636-\frac{\sqrt[]{15}}{2}\left(1-\frac{3}{4}\right)\right]\approx 1\mathrm{,}076.}\end{array}$ A 2 sugarú körszelet területéhez pedig a következő adatok állnak a rendelkezésünkre: $\begin{array}{c}{\displaystyle r_2=\mathrm{2,}{h_2=h}_1=\frac{\sqrt[]{15}}{2}\mathrm{,}{m}_2=\frac{1}{4}\mathrm{.}}\end{array}$ Most is meg kell adnunk a megfelelő $PQ$ körív hosszát. Ehhez a $PKQ$ nagyságát kell ismernünk. A $PKC$ derékszögű háromszögben a $K$-nál lévő $\alpha$ szögre: $\begin{array}{c}{\displaystyle \text{tg}\alpha =\frac{\frac{\sqrt[]{15}}{4}}{\frac{7}{4}}=\frac{\sqrt[]{15}}{7}\mathrm{,}}\end{array}$ ahonnan $PKQ=2\alpha \approx 57\mathrm{,}{91}^{\circ }$. Vagyis $\begin{array}{c}{\displaystyle \frac{i_2}{4\pi }=\frac{57\mathrm{,}{91}^{\circ }}{{360}^{\circ }}\mathrm{,}\text{azaz}{i}_2\approx 2\mathrm{,}021.}\end{array}$ Megint behelyettesítünk a területképletbe: $\begin{array}{c}{\displaystyle T_2=\frac{1}{2}\left[2\cdot 2\mathrm{,}021-\frac{\sqrt[]{15}}{2}\left(2-\frac{1}{4}\right)\right]\approx 0\mathrm{,}327.}\end{array}$ A sötétebb színnel színezett rész területe $T_1+T_2=1\mathrm{,}076+0\mathrm{,}327=1\mathrm{,}403$, a fülbevaló területe pedig $\pi$. Vagyis a fülbevaló kb. 44,7%-a sötétebb árnyalatú.   8. Egy harmadfokú függvényről tudjuk, hogy $f\left(2\right)=f\left(4\right)=4$, a harmadfokú tag együtthatója $1$, továbbá $\begin{array}{c}{\displaystyle \underset{2}{\overset{6}{\int }}f\left(x\right)dx=16.}\end{array}$ Írjuk fel a függvénygörbe érintőjének egyenletét a görbe $5$ abszcisszájú pontjában.  (16 pont)   Megoldás. A harmadfokú függvény hozzárendelési szabálya: $f\left(x\right)=x^3+b{x}^2+cx+d$. Tudjuk, hogy: $\begin{array}{c}{\displaystyle f\left(2\right)=8+4b+2c+d=\mathrm{4,}f\left(4\right)=64+16b+4c+d=4.}\end{array}$ Továbbá: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \underset{2}{\overset{6}{\int }}f\left(x\right)dx}& {\displaystyle =\underset{2}{\overset{6}{\int }}\left(x^3+b{x}^2+cx+d\right)dx={\left[\frac{x^4}{4}+b\cdot \frac{x^3}{3}+c\cdot \frac{x^2}{2}+d\cdot x\right]}_2^6=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left(\frac{6^4}{4}+b\cdot \frac{6^3}{3}+c\cdot \frac{6^2}{2}+d\cdot 6\right)-\left(\frac{2^4}{4}+b\cdot \frac{2^3}{3}+c\cdot \frac{2^2}{2}+d\cdot 2\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left(324+72b+18c+6d\right)-\left(4+\frac{8}{3}b+2c+2d\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{208}{3}b+16c+4d+320=16.}\hfill \end{array}}$ A kapott három egyenlet rendezése után a következő egyenletrendszert kapjuk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 4b+2c+d}& {\displaystyle =-\mathrm{4,}}\hfill \\ \hfill {\displaystyle 16b+4c+d}& {\displaystyle =-\mathrm{60,}}\hfill \\ \hfill {\displaystyle 208b+48c+12d}& {\displaystyle =-912.}\hfill \end{array}}$ Az egyenletrendszer megoldása: $b=-12$, $c=44$, $d=-44$, azaz a harmadfokú függvény hozzárendelési szabálya: $f\left(x\right)=x^3-12x^2+44x-44$. Meghatározzuk a keresett érintő meredekségét. Mivel $f\text{'}\left(x\right)={3x}^2-24x+44$, így $f\text{'}\left(5\right)={3\cdot 5}^2-24\cdot 5+44=-1$. Az érintő meredeksége: $m=-1$. Mivel $f\left(5\right)=5^3-12\cdot 5^2+44\cdot 5-44=1$, ezért az érintési pont koordinátái: $E\left(5;1\right)$. Az $E\left(5;1\right)$ pontra illeszkedő, $m=-1$ meredekségű érintő egyenlete: $x+y=6$.     9. Oldjuk meg a következő egyenletet: $\begin{array}{c}{\displaystyle {\left(x^2-{2013}^2\right)}^2-1=8052x\mathrm{.}}\end{array}$ (16 pont)     Megoldás. Végezzük el a négyzetre emelést és adjunk mindkét oldalhoz 1-et: $\begin{array}{c}{\displaystyle x^4-2\cdot {2013}^2\cdot x^2+{2013}^4=8052x+1.}\end{array}$ Adjunk mindkét oldalhoz $4\cdot {2013}^2\cdot x^2$-et, ekkor a bal oldalon továbbra is teljes négyzet lesz, és a jobb oldalon is kialakul egy teljes négyzet: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(x^2+{2013}^2\right)}^2}& {\displaystyle =4\cdot {2013}^2\cdot x^2+8052x+\mathrm{1,}}\hfill \\ \hfill {\displaystyle {\left(x^2+{2013}^2\right)}^2}& {\displaystyle ={\left(2\cdot 2013x+1\right)}^2\mathrm{.}}\hfill \end{array}}$ Rendezzük nullára az egyenletet, és bontsuk szorzattá az $a^2-b^2=\left(a-b\right)\left(a+b\right)$ azonosság segítségével: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(x^2+{2013}^2\right)}^2-{\left(2\cdot 2013x+1\right)}^2}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle \left(x^2+{2013}^2-2\cdot 2013x-1\right)\left(x^2+{2013}^2+2\cdot 2013x+1\right)}& {\displaystyle =0.}\hfill \end{array}}$ Mindkét tényezőt tovább alakíthatjuk: $\begin{array}{c}{\displaystyle \left[{\left(x-2013\right)}^2-1\right]\cdot \left[{\left(x+2013\right)}^2+1\right]=0.}\end{array}$ Az első tényezőt tovább bonthatjuk szorzattá: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \left(x-2013-1\right)\cdot \left(x-2013+1\right)\cdot \left[{\left(x+2013\right)}^2+1\right]}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle \left(x-2014\right)\cdot \left(x-2012\right)\cdot \left[{\left(x+2013\right)}^2+1\right]}& {\displaystyle =0.}\hfill \end{array}}$ A harmadik tényező minden $x$ esetén pozitív. Az első két tényezőből kapunk megoldást: $x_1=2014$, $x_2=2012$. Mivel átalakításaink ekvivalensek voltak, ezért ezek az eredeti egyenletnek is a megoldásai.