Cím:	Megoldásvázlatok a 2011/4. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Számadó László
Füzet:	2011/május, 269 - 275. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldásvázlatok a 2011/4. sz. emelt szintű gyakorló feladataihoz   I. rész     1. Oldjuk meg a valós számok halmazán az alábbi egyenletet: $\begin{array}{c}{\displaystyle \frac{2x^2-1961x+4000}{x^2-2011x+2010}-\frac{x^2+51x-20}{\left(x-2010\right)\left(x-1\right)}=0.}\end{array}$ (11 pont)     Megoldás. A két nevező egyenlő. A feladat értelmezési tartománya: $x\in \text{R}\backslash \left\{1;2010\right\}$. A számlálók különbségének nullát kell adnia: $\begin{array}{c}{\displaystyle \left(2x^2-1961x+4000\right)-\left(x^2+51x-20\right)=0.}\end{array}$ A következő másodfokú egyenletet kapjuk: $x^2-2012x+4020=0$. A gyökök: $x_1=2$, $x_2=2010$. A feladat megoldása az $x_1=2$, mert csak ez van benne az értelmezési tartományban.   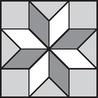2. Nagymama konyháját az ábrán látható négyzet alakú járólapokkal burkolták. A lap belsejében a mintát alkotó szakaszok mindegyike $\mathrm{5,8}\text{cm}$ hosszú. A nyolc egybevágó rombuszból négy fehér, négy piros, a lap többi része szürke.     $a)$ Adjuk meg egy járólap méretét milliméterre kerekítve.   $b)$ A járólap területének hány százaléka piros, és hány százaléka szürke?   $c)$ Egy járólapot a középpontján át, két fehér rombusz átlója mentén kettévágunk. Milyen hosszú a vágás?  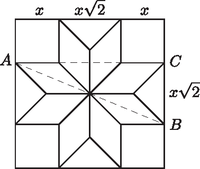(13 pont)   Megoldás. $a)$ A rombuszok egybevágók, ezért mindegyiknek a hegyesszöge ${45}^{\circ }$-os (hiszen nyolc darab alkot egy teljesszöget). A rombuszok tompaszögei ezek alapján ${135}^{\circ }$-osak. Tovább számolva kapjuk, hogy a sarkokban négyzetek láthatók, a háromszögek pedig egyenlő szárú derékszögű háromszögek. Ezek alapján használhatjuk az ábra jelöléseit. A négyzet alakú járólap oldala: $a=2x+x\sqrt[]{2}=x\left(2+\sqrt[]{2}\right)$, ahol $x=5\mathrm{,}8$ cm. Vagyis milliméterre kerekítve: $a\approx 19\mathrm{,}8$ cm.     $b)$ A járólap területe: $T=5\mathrm{,}{8}^2\cdot {\left(2+\sqrt[]{2}\right)}^2\approx 392\mathrm{,}14$ (cm${}^2)$. A szürke rész hat darab 5,8 cm oldalhosszúságú négyzet területével egyenlő: $\begin{array}{c}{\displaystyle t_{\text{szürke}}=6\cdot 5\mathrm{,}{8}^2=201\mathrm{,}84{\text{(cm}}^2)\mathrm{.}}\end{array}$ A maradék fele piros: $\begin{array}{c}{\displaystyle t_{\text{piros}}=\frac{392\mathrm{,}14-201\mathrm{,}84}{2}=95\mathrm{,}15{\text{(cm}}^2)\mathrm{.}}\end{array}$ Százalékokat kell meghatároznunk: $\begin{array}{c}{\displaystyle \frac{201\mathrm{,}84\cdot 100}{392\mathrm{,}14}\approx 51\mathrm{,}\mathrm{47,}\text{illetve}\frac{95\mathrm{,}15\cdot 100}{392\mathrm{,}14}\approx 24\mathrm{,}26.}\end{array}$ Vagyis a szürke rész kb. 51,47%, a piros rész pedig kb. 24,26%. $c)$ Az $ABC$ derékszögű háromszög $AB$ átmérőjének hosszát kell meghatároznunk. Tudjuk, hogy $BC=5\mathrm{,}8\cdot \sqrt[]{2}$, $AC=5\mathrm{,}8\cdot \left(2+\sqrt[]{2}\right)$. Alkalmazzuk a Pitagorasz-tételt: $\begin{array}{c}{\displaystyle AB=\sqrt[]{{\left(5\mathrm{,}8\cdot \sqrt[]{2}\right)}^2+5\mathrm{,}{8}^2\cdot {\left(2+\sqrt[]{2}\right)}^2}\approx 21\mathrm{,}4.}\end{array}$ Vagyis a vágás hossza kb. 21,4 cm.     3. Határozzuk meg azt a pozitív egész $x$ értéket, amelyre a következő összeg egészekre kerekítve $2540$ lesz. $\begin{array}{c}{\displaystyle \text{log}{}_x\left(5\cdot \sqrt[]{\frac{1}{2}}\right)+\text{log}{}_x\left(5^2\cdot \sqrt[]{\frac{2}{3}}\right)+\text{log}{}_x\left(5^3\cdot \sqrt[]{\frac{3}{4}}\right)+\text{...}+\text{log}{}_x\left(5^{99}\cdot \sqrt[]{\frac{99}{100}}\right)\mathrm{.}}\end{array}$ $$(13 pont)     Megoldás. Használjuk a szorzat logaritmusára vonatkozó azonosságot: $\begin{array}{c}{\displaystyle \text{log}{}_{x}5+\text{log}{}_x\sqrt[]{\frac{1}{2}}+\text{log}{}_x{5}^2+\text{log}{}_x\sqrt[]{\frac{2}{3}}+\text{log}{}_x{5}^3+\text{log}{}_x\sqrt[]{\frac{3}{4}}+\text{...}+\text{log}{}_x{5}^{99}+\text{log}{}_x\sqrt[]{\frac{99}{100}}\mathrm{.}}\end{array}$ Csoportosítsuk a tagokat: $\begin{array}{c}{\displaystyle \left(\text{log}{}_{x}5+\text{log}{}_x{5}^2+\text{...}+\text{log}{}_x{5}^{99}\right)+\left(\text{log}{}_x\sqrt[]{\frac{1}{2}}+\text{log}{}_x\sqrt[]{\frac{2}{3}}+\text{...}+\text{log}{}_x\sqrt[]{\frac{99}{100}}\right)\mathrm{.}}\end{array}$ Az első zárójeles kifejezést tovább alakítjuk a hatvány logaritmusára vonatkozó azonosság felhasználásával: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{log}{}_{x}5+\text{log}{}_x{5}^2+\text{...}+\text{log}{}_x{5}^{99}=1\cdot \text{log}{}_{x}5+2\cdot \text{log}{}_{x}5+\text{...}+99\cdot \text{log}{}_{x}5=}\hfill \\ \hfill {\displaystyle =\left(1+2+3+\text{...}+99\right)\cdot \text{log}{}_{x}5=\frac{99\cdot \left(99+1\right)}{2}\cdot \text{log}{}_{x}5=4950\cdot \text{log}{}_{x}5.}\hfill \end{array}}$ Most a második zárójelben lévő összeget hozzuk egyszerűbb alakra: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{log}{}_x\sqrt[]{\frac{1}{2}}+\text{log}{}_x\sqrt[]{\frac{2}{3}}+\text{...}+\text{log}{}_x\sqrt[]{\frac{99}{100}}=\text{log}{}_x\left(\sqrt[]{\frac{1}{2}}\sqrt[]{\frac{2}{3}}\text{...}\sqrt[]{\frac{99}{100}}\right)=}\hfill \\ \hfill {\displaystyle =\text{log}{}_x\sqrt[]{\frac{1}{2}\cdot \frac{2}{3}\cdot \text{...}\cdot \frac{99}{100}}=\text{log}{}_x\sqrt[]{\frac{1}{100}}=\text{log}{}_x\frac{1}{10}\mathrm{.}}\hfill \end{array}}$ Vagyis: $\begin{array}{c}{\displaystyle 4950\cdot \text{log}{}_{x}5+\text{log}{}_{x}0\mathrm{,}1=4950\cdot \frac{\text{lg}5}{\text{lg}x}-\frac{1}{\text{lg}x}=\frac{4950\cdot \text{lg}5-1}{\text{lg}x}\mathrm{.}}\end{array}$   Mivel $\frac{4950\cdot \text{lg}5-1}{\text{lg}x}$ egészekre kerekített értéke 2540, azért $2539\mathrm{,}5<\frac{4950\cdot \text{lg}5-1}{\text{lg}x}<2541\mathrm{,}5$, amiből következik az is, hogy $\text{lg}x$ pozitív. Átrendezés után: $\begin{array}{c}{\displaystyle 1\mathrm{,}360<\frac{4950\cdot \text{lg}5-1}{2541\mathrm{,}5}<\text{lg}x\le \frac{4950\cdot \text{lg}5-1}{2539\mathrm{,}5}<1\mathrm{,}363.}\end{array}$ Mivel a 10-es alapú exponenciális függvény növekedő függvény, azért az egyenlőtlenségek iránya nem változik: $22\mathrm{,}9<x<23\mathrm{,}07$. Egyetlen egész tesz eleget a feladat követelményeinek, mégpedig a 23.     4. Adjuk meg a következő hozzárendeléssel adott függvények legbővebb értelmezési tartományát és a hozzátartozó értékkészletet, ha mindkét halmaz csak egész számokból áll: $\begin{array}{c}{\displaystyle a)f\left(x\right)=\sqrt[]{\frac{5-x}{x+7}};b)g\left(x\right)=\left|\frac{5-x}{x+7}\right|\mathrm{.}}\end{array}$ (14 pont)     Megoldás. $a)$ A négyzetgyök miatt $\frac{5-x}{x+7}\ge 0$, vagyis $x\in \left]-7;5\right]$. Mivel $x$ egész szám, ezért az intervallumot tovább kell szűkítenünk: $x\in \left\{-6;-5;-4;-3;-2;-1;0;1;2;3;4;5\right\}$. Ezek közül csak azok a számok maradhatnak, amelyekre $f\left(x\right)$ is egész. A tizenkét számot könnyen ellenőrizhetjük és két lehetőséget kapunk: $f\left(-1\right)=1$, $f\left(5\right)=0$. Vagyis az $f\left(x\right)$ értelmezési tartománya: $x\in \left\{-1;5\right\}$, az értékkészlete: $f\left(x\right)\in \left\{0;1\right\}$. $b)$ A nevező miatt: $x\ne -7$. Ezen túl csak azok az egész számok maradhatnak, amelyekre $g\left(x\right)$ is egész. Végezzük el a következő átalakítást: $\begin{array}{c}{\displaystyle g\left(x\right)=\left|\frac{5-x}{x+7}\right|=\left|\frac{-\left(x+7\right)+12}{x+7}\right|=\left|-1+\frac{12}{x+7}\right|\mathrm{.}}\end{array}$ Ez csak akkor lehet egész szám, ha $-1+\frac{12}{x+7}$ egész, azaz $x+7$ osztója a 12-nek. Ezek alapján a megfelelő értékeket táblázatban rögzítettük. $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{|ccccccccccccc|}\hline \hfill {\displaystyle x+7}\hfill & \hfill {\displaystyle -12}\hfill & \hfill {\displaystyle -6}\hfill & \hfill {\displaystyle -4}\hfill & \hfill {\displaystyle -3}\hfill & \hfill {\displaystyle -2}\hfill & \hfill {\displaystyle -1}\hfill & \hfill {\displaystyle 1}\hfill & \hfill {\displaystyle 2}\hfill & \hfill {\displaystyle 3}\hfill & \hfill {\displaystyle 4}\hfill & \hfill {\displaystyle 6}\hfill & \hfill {\displaystyle 12}\hfill \\ \hfill {\displaystyle x}\hfill & \hfill {\displaystyle -19}\hfill & \hfill {\displaystyle -13}\hfill & \hfill {\displaystyle -11}\hfill & \hfill {\displaystyle -10}\hfill & \hfill {\displaystyle -9}\hfill & \hfill {\displaystyle -8}\hfill & \hfill {\displaystyle -6}\hfill & \hfill {\displaystyle -5}\hfill & \hfill {\displaystyle -4}\hfill & \hfill {\displaystyle -3}\hfill & \hfill {\displaystyle -1}\hfill & \hfill {\displaystyle 5}\hfill \\ \hfill {\displaystyle g\left(x\right)}\hfill & \hfill {\displaystyle 2}\hfill & \hfill {\displaystyle 3}\hfill & \hfill {\displaystyle 4}\hfill & \hfill {\displaystyle 5}\hfill & \hfill {\displaystyle 7}\hfill & \hfill {\displaystyle 13}\hfill & \hfill {\displaystyle 11}\hfill & \hfill {\displaystyle 5}\hfill & \hfill {\displaystyle 3}\hfill & \hfill {\displaystyle 2}\hfill & \hfill {\displaystyle 1}\hfill & \hfill {\displaystyle 0}\hfill \\ \hline\end{array}}}\end{array}$ Vagyis a $g\left(x\right)$ értelmezési tartománya: $x\in \left\{-19;-13;-11;-10;-9;-8;-6;-5;-4;-3;-1;5\right\}$, az értékkészlete: $g\left(x\right)\in \left\{0;1;2;3;4;5;7;11;13\right\}$.   II. rész       5. Az $f\left(x\right)$ egy másodfokú függvény, a $g\left(x\right)$ pedig egy lineáris törtfüggvény. Tudjuk, hogy $f\left(0\right)=g\left(0\right)=0$, $f\left(1\right)=g\left(1\right)=-1$, $f\left(3\right)=3$, a $g\left(3\right)$ pedig nem értelmezhető. $a)$ Határozzuk meg az $f\left(44\right)$ értékét. $b)$ Határozzuk meg a $g\left(9\right)$ értékét. $c)$ Hány megoldása lehet az $f\left(x\right)=g\left(x\right)$ egyenletnek? Adjuk meg a gyököket. $\begin{array}{c}\end{array}$ (16 pont)   Megoldás. $a)$ Legyen $f\left(x\right)=a{x}^2+bx+c$ hozzárendelésű másodfokú függvény. Tudjuk, hogy $f\left(0\right)=c=0$, $f\left(1\right)=a+b=-1$, $f\left(3\right)=9a+3b=3$. Az így kapott egyenletrendszer megoldása: $a=1$, $b=-2$, azaz $f\left(x\right)=x^2-2x$. Vagyis $f\left(44\right)={44}^2-2\cdot 44=1848$. $b)$ Legyen $g\left(x\right)=\frac{ax+b}{cx+d}$ hozzárendelésű lineáris törtfüggvény ($c\ne 0$).   Tudjuk, hogy $g\left(0\right)=\frac{b}{d}=0$, ezért $b=0$.   Tudjuk, hogy $g\left(3\right)$ nincs értelmezve, vagyis $g\left(x\right)=\frac{ax}{cx-3c}$. Tudjuk továbbá, hogy $g\left(1\right)=\frac{a}{c-3c}=\frac{a}{-2c}=-1$, azaz $a=2c$. Mindent összevetve: $\begin{array}{c}{\displaystyle g\left(x\right)=\frac{2cx}{cx-3c}=\frac{2x}{x-3}\mathrm{,}\text{vagyis}g\left(9\right)=\frac{2\cdot 9}{9-3}=3.}\end{array}$ $c)$ Keressük az összes valós $x$ értéket,   amelyre $f\left(x\right)=g\left(x\right)$, vagyis keressük az $x^2-2x=\frac{2x}{x-3}$ egyenlet megoldásait. $\left(x-3\right)$-mal szorozhatunk ($x\ne 3)$. Mivel harmadfokú egyenletet kapunk, ezért legfeljebb három megoldást kaphatunk. A műveletek elvégzése és a rendezés után: $x^3-5x^2+4x=0$. A bal oldalon álló kifejezést szorzattá alakíthatjuk: $x\left(x-1\right)\left(x-4\right)=0$. Vagyis az egyenlet gyökei: 0, 1, 4. 6. Az ábrán látható szürkére festett vaskerítés nyolc egymás melletti résén szeretnénk átdobni egy kislabdát. A kerítés $4\text{cm}$ széles vasrudakból készült. Egy kerítéselem szélessége $164\text{cm}$, magassága $78\text{cm}$ , a labda átmérője $8\text{cm}$. Dobásunk véletlenszerűnek tekinthető, de a kerítéselem téglalapját biztosan eltaláljuk (a labda középpontjával). 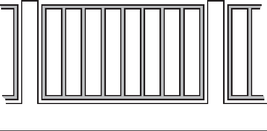    1. ábra   $a)$ Mekkora valószínűséggel tudjuk átdobni a labdát a kerítés résein úgy, hogy az ne érintkezzen a kerítéssel? $b)$ Mekkora labda esetén lesz ez a valószínűség $\mathrm{0,5}$?  (16 pont)   Megoldás. $a)$ Az adatok alapján egy rés mérete 70 cm-szer 16 cm-es téglalap. A labda középpontja ezektől a határvonalaktól legalább 4 cm-re kell, hogy legyen, mert egyébként a labda nekiütközik a vasnak. Vagyis a labda középpontja egy 62 cm-szer 8 cm-es téglalapon haladhat át. A kerítés elem teljes területe: $T=78\cdot 164=12792$ (cm${}^2)$. A kedvező rész területe: $t=8\cdot 62\cdot 8=3968$ (cm${}^2)$. A keresett valószínűség: $\begin{array}{c}{\displaystyle p\left(\text{jó dobás}\right)=\frac{3968}{12792}\approx 0\mathrm{,}31.}\end{array}$ Vagyis kb. 0,31 valószínűséggel tudjuk átdobni a labdát a kerítés résein. $b)$ Legyen a labda sugara $x$ cm. Egy rés mérete 70 cm-szer 16 cm-es téglalap. A labda középpontja ezektől a határvonalaktól legalább $x$ cm-re kell, hogy legyen. A labda középpontja egy $\left(70-2x\right)$ cm-szer $\left(16-2x\right)$ cm-es téglalapon haladhat át. A kerítés elem teljes területe: $T=12792$ cm${}^2$. Most a kedvező rész területe: $t=8\left(70-2x\right)\left(16-2x\right)$ cm${}^2$. A keresett valószínűség: ${\displaystyle \begin{array}{c}\hfill {\displaystyle p\left(\text{jó dobás}\right)=\frac{8\left(70-2x\right)\left(16-2x\right)}{12792}=0\mathrm{,}\mathrm{5,}}\hfill \\ \hfill {\displaystyle \left(70-2x\right)\left(16-2x\right)=799\mathrm{,}\mathrm{5,}}\hfill \\ \hfill {\displaystyle 4x^2-172x+320\mathrm{,}5=\mathrm{0,}}\hfill \\ \hfill {\displaystyle x_{1;2}=\frac{172\pm \sqrt[]{{172}^2-5128}}{8}\approx \{{\displaystyle \begin{array}{c}{\displaystyle 41\mathrm{,}\mathrm{05,}}\hfill \\ {\displaystyle 1\mathrm{,}95.}\hfill \end{array}}}\hfill \end{array}}$ Mivel egy rés 16 cm széles, ezért a labda sugara nem lehet nagyobb, mint 8 cm. Vagyis a labda sugara csak az $x_2$ lehet. Ezek alapján a labda átmérője milliméter pontossággal: 3,9 cm.     7. Adott a koordinátarendszerben az $S\left(-1;3\right)$ és az $L\left(9;3\right)$ pont. $a)$ Adjuk meg azokat a $Z$ pontokat koordinátáikkal, amelyekre az $SZL$ háromszög derékszögű és a területe $20$. $b)$ Adjuk meg azoknak a $Z\left(x;y\right)$ pontoknak a halmazát, amelyekre $S{Z}^2+L{Z}^2=68$. $\begin{array}{c}\end{array}$ (16 pont)   Megoldás. $a)$ Három eset lehetséges. I. eset: a derékszög az $S$ csúcsnál található. Mivel $SL=10$, ezért $SZ=4$, hiszen így lesz a háromszög területe 20. Azaz két megfelelő pont létezik: $Z_1\left(-1;7\right)$, $Z_2\left(-1;-1\right)$. II. eset: a derékszög az $L$ csúcsnál van. Az előző esethez hasonlóan kapjuk a következő két pontot: $Z_3\left(9;7\right)$, $Z_4\left(9;-1\right)$. III. eset: a derékszög a $Z$ csúcsnál helyezkedik el. Ekkor a keresett pontok az $SL$ átmérőjű Thalész-körre illeszkednek, továbbá az $SL$ egyenestől 4 egységre párhuzamosan futó egyenesre. Ilyen egyenes kettő van, azaz még négy megfelelő pontot találunk. A Thalész-kör egyenlete: ${\left(x-4\right)}^2+{\left(y-3\right)}^2=25$, a két egyenes egyenlete pedig $y=7$, illetve $y=-1$. Ezek alapján a négy pont: $Z_5\left(1;7\right)$, $Z_6\left(1;-1\right)$, $Z_7\left(7;7\right)$, $Z_8\left(7;-1\right)$. Vagyis nyolc megfelelő $Z$ pont található. $b)$ Írjuk fel a két pont távolságára ismert összefüggést: ${\displaystyle \begin{array}{c}\hfill {\displaystyle S{Z}^2+L{Z}^2=\left[{\left(x+1\right)}^2+{\left(y-3\right)}^2\right]+\left[{\left(x-9\right)}^2+{\left(y-3\right)}^2\right]=\mathrm{68,}}\hfill \\ \hfill {\displaystyle x^2+2x+1+y^2-6y+9+x^2-18x+81+y^2-6y+9=\mathrm{68,}}\hfill \\ \hfill {\displaystyle x^2-8x+y^2-6y=-\mathrm{16,}}\hfill \\ \hfill {\displaystyle {\left(x-4\right)}^2+{\left(y-3\right)}^2=9.}\hfill \end{array}}$ A keresett ponthalmaz a $K\left(4;3\right)$ középpontú, $r=3$ sugarú kör.     8. Oldjuk meg a következő egyenletet: $\begin{array}{c}{\displaystyle \sqrt[]{\text{sin}{}^{6}x+\text{cos}{}^{6}x}+\sqrt[]{\text{sin}{}^{4}x+\text{cos}{}^{4}x}+\sqrt[]{\text{sin}{}^{2}x+\text{cos}{}^{2}x}=\frac{3\sqrt[]{2}+2}{2\sqrt[]{2}}\mathrm{.}}\end{array}$ (16 pont)     Megoldás. Tudjuk, hogy $\text{sin}{}^{2}x+\text{cos}{}^{2}x=1$ minden $x$-re, ezért ennyivel csökkenthetjük mindkét oldal értékét: $\begin{array}{c}{\displaystyle \sqrt[]{\text{sin}{}^{6}x+\text{cos}{}^{6}x}+\sqrt[]{\text{sin}{}^{4}x+\text{cos}{}^{4}x}=\frac{\sqrt[]{2}+2}{2\sqrt[]{2}}\mathrm{.}}\end{array}$ A négyzetgyök alatti kifejezéseket átalakítjuk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle A}& {\displaystyle =\text{sin}{}^{6}x+\text{cos}{}^{6}x={\left(\text{sin}{}^{2}x+\text{cos}{}^{2}x\right)}^3-3\text{sin}{}^{2}x\text{cos}{}^{2}x\left(\text{sin}{}^{2}x+\text{cos}{}^{2}x\right)=1-\frac{3}{4}\text{sin}{}^{2}2x\mathrm{,}}\hfill \\ \hfill {\displaystyle B}& {\displaystyle =\text{sin}{}^{4}x+\text{cos}{}^{4}x={\left(\text{sin}{}^{2}x+\text{cos}{}^{2}x\right)}^2-2\text{sin}{}^{2}x\text{cos}{}^{2}x=1-\frac{1}{2}\text{sin}{}^{2}2x\mathrm{.}}\hfill \end{array}}$ Mivel $0\le \text{sin}{}^{2}2x\le 1$, ezért $\frac{1}{4}\le A\le 1$ és $\frac{1}{2}\le B\le 1$. Az egyenlet bal oldalán lévő két négyzetgyökös kifejezés minimumértékének összege: $\sqrt[]{\frac{1}{4}}+\sqrt[]{\frac{1}{2}}$, ami $\frac{\sqrt[]{2}+2}{2\sqrt[]{2}}$ alakban is írható.   Vagyis egyenletünknek akkor van megoldása, ha mindkét négyzetgyökös kifejezés a minimumértéket veszi fel. Ez csak a $\text{sin}{}^{2}2x=1$ esetén valósul meg, azaz $\text{sin}2x=1$ vagy $\text{sin}2x=-1$. Ebből kapjuk, hogy $2x=\frac{\pi }{2}+k\pi$ ($k\in \text{Z}$). Tehát az egyenlet megoldása: $\begin{array}{c}{\displaystyle x=\frac{\pi }{4}+k\cdot \frac{\pi }{2}\left(k\in \text{Z}\right)\mathrm{.}}\end{array}$     9. 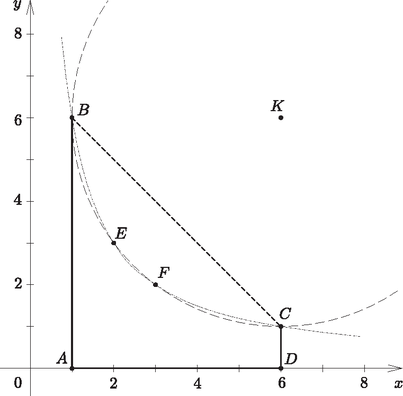Az $A\left(1;0\right)$, $B\left(1;6\right)$, $C\left(6;1\right)$, $D\left(6;0\right)$ pontok által meghatározott négyszög $BC$ oldalát először helyettesítsük a $K\left(6;6\right)$ középpontú és $r=5$ sugarú kör $B$ és $C$ közötti rövidebb ívével, másodszor pedig az $f\left(x\right)=\frac{6}{x}$ hozzárendeléssel adott függvény grafikonjának a $B$ és $C$ közötti darabjával. $a)$ Határozzuk meg mindkét esetben az $ABCD$ síkidom területét. Melyik a nagyobb? $b)$ Adjuk meg a $B$ és $C$ pontokat összekötő két görbe vonal közös pontjainak koordinátáit.  (16 pont)   Megoldás. $a)$ Az első esetben az $ABKD$ téglalapból hiányzik egy $K$ középpontú, $r=5$ sugarú negyedkör. Vagyis ebben az esetben a terület: $\begin{array}{c}{\displaystyle T_1=5\cdot 6-\frac{5^2\cdot \pi }{4}=\frac{120-25\pi }{4}\approx 10\mathrm{,}365.}\end{array}$     A második esetben a területet a következő integrállal számíthatjuk ki: $\begin{array}{c}{\displaystyle T_2=\underset{1}{\overset{6}{\int }}\frac{6}{x}dx=6\cdot \underset{1}{\overset{6}{\int }}\frac{1}{x}dx=6\cdot {\left[\text{ln}|x|\right]}_1^6=6\cdot \left(\text{ln}6-\text{ln}1\right)=6\cdot \text{ln}6\approx 10\mathrm{,}751.}\end{array}$ Vagyis a második esethez tartozó síkidom területe a nagyobb 0,386-del. $b)$ Az első esethez tartozó körív egyenlete: ${\left(x-6\right)}^2+{\left(y-6\right)}^2=25$. A $BC$ húrhoz tartozó rövidebb körív, mint grafikon, a következő függvényhez tartozik: $\begin{array}{c}{\displaystyle g\left(x\right)=6-\sqrt[]{25-{\left(x-6\right)}^2}\mathrm{,}\text{ahol}x\in \left[1;6\right]\mathrm{.}}\end{array}$ A második esetben az $f\left(x\right)=\frac{6}{x}$ hozzárendelésű függvényről van szó, ahol $x\in \left[1;6\right]$. A feladat az $f\left(x\right)=g\left(x\right)$ egyenlet megoldása az $\left[1;6\right]$ intervallumon: $\begin{array}{c}{\displaystyle \frac{6}{x}=6-\sqrt[]{25-{\left(x-6\right)}^2}\mathrm{.}}\end{array}$ A vizsgált intervallumon végezzük el a következő átalakításokat: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \sqrt[]{25-x^2+12x-36}=6-\frac{6}{x}\mathrm{,}}\hfill \\ \hfill {\displaystyle x\sqrt[]{-x^2+12x-11}=6x-\mathrm{6,}}\hfill \\ \hfill {\displaystyle x^2\left(-x^2+12x-11\right)=36x^2-72x+\mathrm{36,}}\hfill \\ \hfill {\displaystyle 0=x^4-12x^3+47x^2-72x+36.}\hfill \end{array}}$ A feladat szövegéből következik, hogy az $x_1=1$, valamint az $x_2=6$ megoldása az egyenletnek (hiszen mindkét görbére illeszkedik a $B$ és a $C$ pont). Ezért az egyenlet a következő alakban is írható: $0=\left(x-1\right)\left(x-6\right)\left(x^2+ax+b\right)$. Végezzük el a szorzásokat, az együtthatókat összehasonlítva az előbb kapott negyedfokú egyenlet megfelelő együtthatóival kapjuk, hogy $b=6$, $a=-5$. Vagyis $\begin{array}{c}{\displaystyle 0=\left(x-1\right)\left(x-6\right)\left(x^2-5x+6\right)=\left(x-1\right)\left(x-6\right)\left(x-2\right)\left(x-3\right)\mathrm{.}}\end{array}$ További két megoldás: $x_3=2$, $x_4=3$. Tehát a $B\left(1;6\right)$ és a $C\left(6;1\right)$ pontok mellett még két közös pontja van a két görbének: $E\left(2;3\right)$, $F\left(3;2\right)$.