Cím:	Megoldásvázlatok a 2011/3. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Gedeon Veronika
Füzet:	2011/április, 196 - 203. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. A királyfi Csipkerózsikához sietett a toronyba. Először egyesével, majd kettesével, végül már hármasával vette a lépcsőfokokat a $232$ fokos csigalépcsőn. Ha az elején lépett volna hármasával, majd kettesével, végül egyesével rendre ugyanennyit, akkor egy $276$ fokos lépcsősor tetejére is feljuthatott volna. $a)$ Mennyit lépett a királyfi, míg felért a lépcső tetejére? $b)$ Hány lépcsőt lépett egyesével, ha kettesével másfélszer annyit lépett, mint hármasával?  (10 pont)   Megoldás. $a)$ Legyen az egyesével tett lépések száma $x$, a kettes lépéseké $y$, a hármasoké $z$. A feladat szövege szerint: $\begin{array}{c}{\displaystyle x+2y+3z=\mathrm{232,}3x+2y+z=276.}\end{array}$ Adjuk össze a két egyenletet, és osszunk 4-gyel: $x+y+z=127$. Vagyis 127 lépéssel ért fel a lépcső tetejére. $b)$ Tudjuk, hogy $y=1\mathrm{,}5z$. A három ismeretlenre így már három egyenletünk van. Ennek megoldása: $x=52$, $y=45$, $z=30$. Tehát a királyfi 52 lépcsőt lépett egyesével.   2. Három kétjegyű prímszám egy számtani sorozat három egymást követő tagja. Az összegük olyan háromjegyű szám, melyben a számjegyek egy növekvő számtani sorozat három egymást követő tagját adják. A számjegyek közötti különbségnek a másfélszerese a prímszámok közötti különbség. Melyik ez a három prímszám?  (13 pont)   Megoldás. Mivel a prímszámok kétjegyűek, így az összegük 300-nál kisebb, és tudjuk, hogy a számjegyek is számtani sorozatot alkotnak. Ilyen háromjegyű számok a következők: 123, 135, 147, 159, 234, 246, 258. Az összeg harmada adja a középső prímszámot. A harmadolás után csak két esetben kapunk prímszámot: 123, 159. I. eset: Ha az összeg 123, akkor a középső prímszám a 41. Mivel a számjegyek különbsége 1, ezért a prímeknél 1,5 lesz a különbség. Ezek alapján nem kapunk egész számokat. II. eset: Ha az összeg 159, akkor a középső prímszám az 53. Mivel a számjegyek különbsége 4, ezért a prímeknél 6 lesz a különbség. Ezek alapján a három szám: 47, 53, 59, és ezek mindegyike prímszám, vagyis megfelel a feladat feltételeinek.   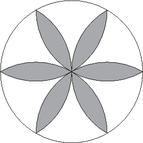3. Bori a körzőjével hatszirmú virágot szerkesztett az ábrán látható módon, majd kiszínezte.     $a)$ Mekkorára nyitotta a körzőjét Bori, ha a hatszirmú virág határvonalának hossza $18\pi$ cm-ben? $b)$ A kör területének hány százalékát színezte ki?  (14 pont)   Megoldás. $a)$ Legyen a kör sugara $r$, ekkor kerülete $K=2r\pi$. A virág egy szirmának egyik íve a kör ${60}^{\circ }$-os középponti szögéhez tartozó ív hosszával egyenlő, tehát a kör kerületének hatoda. A virág 12 db ugyanekkora ívből áll. Tehát összesen a kör kerületének kétszerese a virág határvonalának hossza, azaz: $2K=4r\pi =18\pi$. Ebből $r=4\mathrm{,}5$. Vagyis 4,5 cm-re nyitotta ki Bori a körzőjét. $b)$ A kör területe: $T=r^2\pi$. A virág egy szirmának (a kör sugara által levágott) fele a kör ${60}^{\circ }$-os középponti szögéhez tartozó körszelet. A körszelet ívének hossza: $i=\frac{2r\pi }{6}=\frac{r\pi }{3}$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_{\text{körszelet}}}& {\displaystyle =\frac{ir}{2}-\frac{r^2\text{sin}{60}^{\circ }}{2}=\frac{\frac{r\pi }{3}r}{2}-\frac{r^2\frac{\sqrt[]{3}}{2}}{2}=\frac{r^2}{12}\left(2\pi -3\sqrt[]{3}\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle T_{\text{virág}}}& {\displaystyle =12\cdot T_{\text{körszelet}}=r^2\left(2\pi -3\sqrt[]{3}\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{T_{\text{virág}}}{T}}& {\displaystyle =\frac{r^2\left(2\pi -3\sqrt[]{3}\right)}{r^2\pi }=\frac{2\pi -3\sqrt[]{3}}{\pi }\approx 0\mathrm{,}346.}\hfill \end{array}}$ Tehát kb. a kör 34,6%-át színezte ki Bori.   4. Oldjuk meg az alábbi egyenletet a valós számok halmazán: $\begin{array}{c}{\displaystyle \text{log}{}_5\left(x-2\right)+\text{log}{}_{25}\left(4x^3+29x^2+16x\right)=\text{log}{}_5\left(x^3-8\right)\mathrm{.}}\end{array}$ (14 pont)   Megoldás. A feladat értelmezési tartománya: $x>2$. A logaritmus azonosságait és a logaritmus függvény kölcsönös egyértelműségét felhasználva: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{\text{log}{}_5\left(4x^3+29x^2+16x\right)}{\text{log}{}_{5}25}}& {\displaystyle =\text{log}{}_5\left(x^3-8\right)-\text{log}{}_5\left(x-2\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{\text{log}{}_5\left(4x^3+29x^2+16x\right)}{2}}& {\displaystyle =\text{log}{}_5\left(x^2+2x+4\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{log}{}_5\left(4x^3+29x^2+16x\right)}& {\displaystyle =\text{log}{}_5{\left(x^2+2x+4\right)}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle 4x^3+29x^2+16x}& {\displaystyle =x^4+4x^3+12x^2+16x+\mathrm{16,}}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle =x^4-17x^2+16.}\hfill \end{array}}$ Ez $x^2$-re másodfokú egyenlet, a gyökök: $x_1=-1$, $x_2=1$, $x_3=-4$, $x_4=4$, melyek közül csak az $x=4$ a megoldás az értelmezési tartomány miatt.   II. rész     5. Adott a síkon $2011$ egyenes, melyek között nincsenek párhuzamosok, továbbá $1011$ egyenes átmegy a sík $P$ pontján. A $P$-n kívül a sík egyetlen pontjára sem illeszkedik kettőnél több egyenes. $a)$ Hány metszéspontja van a $2011$ egyenesnek? $b)$ Mekkora valószínűséggel van $3$ véletlenszerűen választott egyenesnek közös pontja? $c)$ Mekkora a valószínűsége annak, hogy $3$ véletlenszerűen választott egyenes egy háromszög három oldalegyenese? $d)$ Az egyenesek közül kiválasztunk ötöt. Az általuk meghatározott tartományokat kiszínezzük a lehető legkevesebb színnel úgy, hogy az élben szomszédos részek ne legyenek azonos színűek. Hány színre lesz szükségünk?  (16 pont)   Megoldás. $a)$ A 2011 darab egyenesnek $\left(\genfrac{}{}{0ex}{}{2011}{2}\right)$ metszéspontja lehet maximálisan. Most ebből 1011 egyenesnek az $\left(\genfrac{}{}{0ex}{}{1011}{2}\right)$ metszéspontja helyett csak egy metszéspont van. Ezek szerint a metszéspontok száma: $\left(\genfrac{}{}{0ex}{}{2011}{2}\right)-\left(\genfrac{}{}{0ex}{}{1011}{2}\right)+1=1510501$. A feltételeknek megfelelő 2011 darab egyenesnek 1 510 501 metszéspontja van. $b)$ Véletlenszerűen választunk három egyenest, ekkor az összes lehetőségek száma: $\left(\genfrac{}{}{0ex}{}{2011}{3}\right)$. Csak az a kedvező, ha az 1011-ből választunk hármat. A kedvező esetek száma: $\left(\genfrac{}{}{0ex}{}{1011}{3}\right)$. A keresett valószínűség: $\begin{array}{c}{\displaystyle \frac{\left(\genfrac{}{}{0ex}{}{1011}{3}\right)}{\left(\genfrac{}{}{0ex}{}{2011}{3}\right)}\approx 0\mathrm{,}127.}\end{array}$ $c)$ Mivel közülük semelyik kettő nem párhuzamos, azért ha a három egyenes nem egy pontban metszi egymást, akkor háromszöget határoznak meg. Tudjuk, hogy a véletlenszerűen választott három egyenes kb. 0,127 valószínűséggel metszi egy pontban egymást, ezért annak valószínűsége, hogy a három egyenes egy háromszög három oldalegyenese lesz, 0,873. $d)$ Egy egyenes a síkot két részre osztja, ekkor két szín biztosan elég a színezéshez. Ezután egy újabb egyenes hozzávételekor mindig az egyik félsík összes darabjának színét ellenkezőjére változtatjuk, így biztosítva, hogy a szomszédos területek továbbra is különböző színűek maradjanak. Tehát a színezéshez két szín elég.       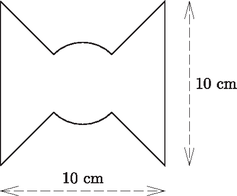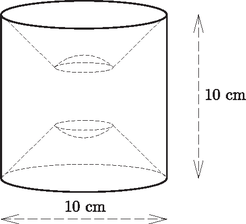6. Egy esztergályos megrendelést kapott forgásszimmetrikus díszítőelemek készítésére. A megrendelő az ábrán látható tengelymetszetet adta le, de elfelejtette bejelölni a forgástengelyt.     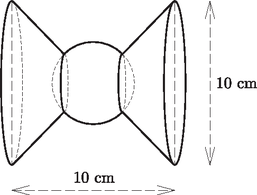A díszítőelemeket olyan hengerből kell elkészíteni, amelyek átmérője és magassága is 10 cm, a kész elem közepén látható gömb átmérője pedig 5 cm. Az esztergályos mindkét lehetséges változatból elkészített egy-egy mintapéldányt. Hány százalék a hulladék az egyes esetekben?  (16 pont)   I. megoldás. Mindkét esetben ugyanakkora a kiindulásnak vett henger térfogata: $V_{\text{henger}}=5^2\pi \cdot 10=250\pi \approx 785\mathrm{,}40$, és a gömb térfogata: $\begin{array}{c}{\displaystyle V_{\text{gömb}}=\frac{4\pi }{3}2\mathrm{,}{5}^3=\frac{62\mathrm{,}5\pi }{3}\approx 65\mathrm{,}45.}\end{array}$     1. eset: A forgástengely vízszintes. Ennek a változatnak a térfogata: $\begin{array}{c}{\displaystyle V_1=2V_{\text{csonkakúp}}+V_{\text{gömb}}-2V_{\text{gömbszelet}}\mathrm{.}}\end{array}$ A csonkakúp alapkörének sugara megegyezik a henger sugarával, vagyis 5 cm. Meg kell határoznunk a magasságának és a fedőkör sugarának a hosszát. Használjuk a keresztmetszetről készített ábra jelöléseit.     A $KPB$ és a $KFA$ egyenlőszárú derékszögű háromszögek, ezért hasonlók. Tudjuk, hogy $AF=5$, $KA=5\sqrt[]{2}$, $KB=2\mathrm{,}5$, így a megfelelő oldalak aránya: $\frac{BP}{2\mathrm{,}5}=\frac{5}{5\sqrt[]{2}}$. Ebből kapjuk a csonkakúp fedőkörének sugarát: $BP=1\mathrm{,}25\sqrt[]{2}$. A háromszögek egyenlőszárúságát felhasználva a csonkakúp magassága is kifejezhető: $PF=KF-KP=5-1\mathrm{,}25\sqrt[]{2}$. A csonkakúp térfogata: $\begin{array}{c}{\displaystyle V_{\text{csonkakúp}}=\frac{\pi }{3}\left(5-1\mathrm{,}25\sqrt[]{2}\right)[5^2+5\left(1\mathrm{,}25\sqrt[]{2}\right)+{\left(1\mathrm{,}25\sqrt[]{2}\right)}^2]\approx 125\mathrm{,}11.}\end{array}$ A gömb sugara: $KB=2\mathrm{,}5$, a gömbszelet magassága: $PR=KR-KP=2\mathrm{,}5-1\mathrm{,}25\sqrt[]{2}$. A gömbszelet térfogata: $\begin{array}{c}{\displaystyle V_{\text{gömbszelet}}=\frac{\pi }{3}{\left(2\mathrm{,}5-1\mathrm{,}25\sqrt[]{2}\right)}^2[3\cdot 2\mathrm{,}5-\left(2\mathrm{,}5-1\mathrm{,}25\sqrt[]{2}\right)]\approx 3\mathrm{,}80.}\end{array}$ A kapott eredmények felhasználásával: ${\displaystyle \begin{array}{c}\hfill {\displaystyle V_1=2V_{\text{csonkakúp}}+V_{\text{gömb}}-2V_{\text{gömbszelet}}=2\cdot 125\mathrm{,}11+65\mathrm{,}45-2\cdot 3\mathrm{,}80=308\mathrm{,}\mathrm{07,}}\hfill \\ \hfill {\displaystyle \frac{V_1}{V_{\text{henger}}}=\frac{308\mathrm{,}07}{785\mathrm{,}40}\approx 0\mathrm{,}3922.}\hfill \end{array}}$ Tehát az első esetben az anyagveszteség kb. 60,78%-os.     2. eset: A forgástengely függőleges. Ennek a változatnak a térfogata: $\begin{array}{c}{\displaystyle V_2=V_{\text{henger}}-2V_{\text{csonkakúp}}+2V_{\text{gömbszelet}}\mathrm{.}}\end{array}$ Az előző rész eredményeit felhasználva: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle V_2}& {\displaystyle =V_{\text{henger}}-2V_{\text{csonkakúp}}+2V_{\text{gömbszelet}}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =785\mathrm{,}40-2\cdot 125\mathrm{,}11+2\cdot 3\mathrm{,}80=542\mathrm{,}\mathrm{78,}}\hfill \\ \hfill {\displaystyle \frac{V_2}{V_{\text{henger}}}}& {\displaystyle =\frac{542\mathrm{,}78}{785\mathrm{,}40}=0\mathrm{,}6911.}\hfill \end{array}}$ Tehát a második esetben az anyagveszteség 30,89%-os.   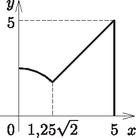II. megoldás. 1. eset: A forgástengely vízszintes.     A kör egyenlete: $x^2+y^2=6\mathrm{,}25$ (ahol $0\le x\mathrm{,}y\le 2\mathrm{,}5)$, ebből $y=\sqrt[]{6\mathrm{,}25-x^2}$. Az egyenes egyenlete: $y=x$. A kör és az egyenes metszéspontja: $\left(1\mathrm{,}25\sqrt[]{2};1\mathrm{,}25\sqrt[]{2}\right)$. A forgástest térfogatát integrállal határozzuk meg: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle V_1}& {\displaystyle =2\pi \left(\underset{0}{\overset{1\mathrm{,}25\sqrt[]{2}}{\int }}\left(6\mathrm{,}25-x^2\right)dx+\underset{1\mathrm{,}25\sqrt[]{2}}{\overset{5}{\int }}{x}^{2}dx\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =2\pi \left({\left[6\mathrm{,}25x-\frac{x^3}{3}\right]}_0^{1\mathrm{,}25\sqrt[]{2}}+{\left[\frac{x^3}{3}\right]}_{1\mathrm{,}25\sqrt[]{2}}^5\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =2\pi \left(6\mathrm{,}25\cdot 1\mathrm{,}25\sqrt[]{2}-\frac{{\left(1\mathrm{,}25\sqrt[]{2}\right)}^3}{3}+\frac{5^3}{3}-\frac{{\left(1\mathrm{,}25\sqrt[]{2}\right)}^3}{3}\right)\approx 308\mathrm{,}08.}\hfill \end{array}}$ Az eredeti henger térfogata: $V_{\text{henger}}=5^2\pi \cdot 10=250\pi \approx 785\mathrm{,}40$. $\begin{array}{c}{\displaystyle \frac{V_1}{V_{\text{henger}}}=\frac{308\mathrm{,}08}{785\mathrm{,}40}\approx 0\mathrm{,}3922.}\end{array}$ Tehát az első esetben az anyagveszteség kb. 60,78%-os. 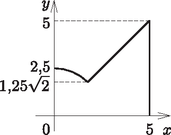II. eset: A forgástengely függőleges.     A forgástest térfogatát integrállal határozzuk meg: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle V_2}& {\displaystyle =2\pi \left(\underset{0}{\overset{5}{\int }}25dy-\underset{1\mathrm{,}25\sqrt[]{2}}{\overset{5}{\int }}{y}^{2}dy+\underset{1\mathrm{,}25\sqrt[]{2}}{\overset{2\mathrm{,}5}{\int }}\left(6\mathrm{,}25-y^2\right)dy\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =2\pi \left({\left[25y\right]}_0^5-{\left[\frac{y^3}{3}\right]}_{1\mathrm{,}25\sqrt[]{2}}^5+{\left[6\mathrm{,}25y-\frac{y^3}{3}\right]}_{1\mathrm{,}25\sqrt[]{2}}^{2\mathrm{,}5}\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =2\pi \left(25\cdot 5-\frac{5^3}{3}+\frac{{\left(1\mathrm{,}25\sqrt[]{2}\right)}^3}{3}+6\mathrm{,}25\cdot 2\mathrm{,}5-\frac{2\mathrm{,}{5}^3}{3}-6\mathrm{,}25\cdot 1\mathrm{,}25\sqrt[]{2}+\frac{{\left(1\mathrm{,}25\sqrt[]{2}\right)}^3}{3}\right)\approx }\hfill \\ \hfill {\displaystyle }& {\displaystyle \approx 542\mathrm{,}77.}\hfill \end{array}}$ Az eredeti henger térfogata: $V_{\text{henger}}\approx 785\mathrm{,}40$. $\begin{array}{c}{\displaystyle \frac{V_2}{V_{\text{henger}}}=\frac{542\mathrm{,}77}{785\mathrm{,}40}\approx 0\mathrm{,}6911.}\end{array}$ Tehát a második esetben az anyagveszteség kb. 30,89%-os.   7. Egy háromszög csúcsainak koordinátái: $A\left(-7;-2\right)$, $B\left(11;-2\right)$, $C\left(-1;10\right)$. $a)$ Adjuk meg a háromszög mindhárom csúcsától egyenlő távolságra található $K$ pont koordinátáit. $b)$ Adjuk meg a háromszög $M$ magasságpontjának koordinátáit. $c)$ Igazoljuk számítással, hogy az $ABC$ háromszögben az $S$ súlypont harmadolja az $MK$ szakaszt.  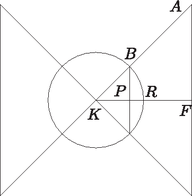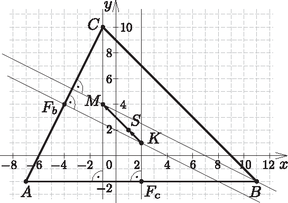(16 pont)   Megoldás. A megoldás során a mellékelt ábra jelöléseit használjuk.     $a)$ A $K$ pont az oldalfelező merőlegesek metszéspontjában található. Írjuk fel a $c$ oldalhoz tartozó $f_c$ felezőmerőleges egyenletét. Ennek az egyenesnek egyik pontja az $AB$ oldal felezőpontja: $F_c\left(2;-2\right)$. Mivel a $c$ oldal párhuzamos az $x$ tengellyel, azért az $f_c$ egyenes az $y$ tengellyel lesz párhuzamos, így egyenlete: $x=2$. Írjuk fel a $b$ oldalhoz tartozó $f_b$ felezőmerőleges egyenletét is. Ennek az egyenesnek egyik pontja az $AC$ oldal felezőpontja: $F_b\left(-4;4\right)$. Az $f_b$ egyenes egy normálvektora: $\overrightarrow{AC}\left(6;12\right)$, aminek számolhatunk a hatodával. Vagyis az $f_b$ egyenes egyenlete: $x+2y=1\cdot \left(-4\right)+2\cdot 4$, amiből $y=-\frac{1}{2}x+2$. Az $f_c$ és $f_b$ egyenesek egyenletéből kapjuk: $K\left(2;1\right)$. $b)$ Az $M$ magasságpont a háromszög magasságainak metszéspontja. Írjuk fel a $c$ oldalhoz tartozó $m_c$ magasság egyenesének egyenletét. Ennek egyik pontja $C\left(-1;10\right)$, és merőleges a $c$ oldalra, ezért egyenlete: $x=-1$. Írjuk fel a $b$ oldalhoz tartozó $m_b$ magasság egyenesének egyenletét. Ennek egyik pontja $B\left(11;-2\right)$, és merőleges a $b$ oldalra, tehát normálvektora megegyezik az oldalfelező merőleges normálvektorával. Vagyis az $m_b$ egyenes egyenlete: $x+2y=1\cdot 11+2\cdot \left(-2\right)$, amiből: $y=-\frac{1}{2}x+\frac{7}{2}$. Az $m_c$ és $m_b$ egyenesek egyenletéből kapjuk: $M\left(-1;4\right)$. $c)$ A súlypont koordinátáit a csúcspontok megfelelő koordinátáinak számtani közepe adja, vagyis: $S\left(1;2\right)$. Mivel $M\left(-1;4\right)$ és $K\left(2;1\right)$, ezért $\overrightarrow{MS}\left(2;-2\right)$, illetve $\overrightarrow{SK}\left(1;-1\right)$. A két vektorra: $\overrightarrow{MS}=2\overrightarrow{SK}$, tehát az $S$ pont az $MK$ szakasz $K$ végpontjához közelebbi harmadolópont.   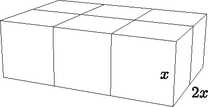8. Anna ajándékba olyan $56{\text{dm}}^3$ térfogatú csomagot kapott, melynek csomagolásához (az ábrán látható módon) a lehető legkevesebb zsineget használták. Mekkora a téglatest alakú doboz éleinek hossza, ha az egyik alapélének hossza egyenlő a magasság kétszeresével az ábra szerint?  (16 pont)       Megoldás. A téglatest élei legyenek $x$, $2x$, $y$. A zsineg hosszúsága a téglatest éleinek függvényében: $l\left(x\mathrm{,}y\right)=6x+4\cdot 2x+2y=14x+2y$, ahol $x\mathrm{,}y>0$. Az ajándék térfogata: $V=56=2x^{2}y$. Ebből kifejezzük $y$-t: $y=\frac{28}{x^2}$, és behelyettesítjük a zsineg hosszúságát leíró függvénybe: $\begin{array}{c}{\displaystyle l\left(x\right)=14x+2y=14x+\frac{56}{x^2}\mathrm{,}}\end{array}$ ahol $x>0$. Ennek a függvénynek keressük a minimumát. Az $l$ függvény deriváltja: $\begin{array}{c}{\displaystyle l\text{'}\left(x\right)=14-\frac{112}{x^3}\mathrm{.}}\end{array}$ Az $l$ függvénynek ott lehet minimuma, ahol a derivált függvény értéke nulla, azaz: $14-\frac{112}{x^3}=0$, ebből $x=2$. Mivel itt a derivált negatívból pozitívba vált, ezért ezen a helyen a függvénynek valóban minimuma van. Ezt visszahelyettesítve kapjuk a doboz éleinek hosszát: 2 dm, 4 dm és 7 dm.   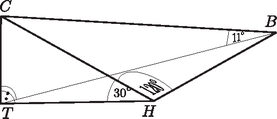9. Az azonos tengerszint feletti magasságban fekvő Hencida és Boncida között a távolság 5 km. Hencidából egy közeli hegy csúcsa ${30}^{\circ }$-os, Boncidából pedig ${11}^{\circ }$-os szögben látszik. Hencidából a hegy csúcsát és Boncidát összekötő szakasz látószöge ${120}^{\circ }$-os. $a)$ Mennyivel van magasabban a hegy csúcsa a két város szintjéhez képest? $b)$ A két várost összekötő egyenes út felénél felröppen egy madár. Röppályájának minden pontja egyenlő távolságra van a két várostól. Mennyire közelítheti meg röpülés közben a hegy csúcsát?  (16 pont)       Megoldás. $a)$ Az ábrán látható jelöléseket használjuk. A hegy magassága $x$. A $CTH$ derékszögű háromszögben $\text{sin}{30}^{\circ }=\frac{x}{a}$, ebből $a=2x$. Ugyanígy a $CTB$ derékszögű háromszögben $\text{sin}{11}^{\circ }=\frac{x}{b}$, ebből $b=\frac{x}{\text{sin}{11}^{\circ }}\approx 5\mathrm{,}24x$. Írjuk fel a $CHB$ háromszögben a koszinusztételt a $b$ oldalra, majd helyettesítsük be az imént kapott összefüggéseket: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle b^2}& {\displaystyle =a^2+5^2-2\cdot a\cdot 5\cdot \text{cos}{120}^{\circ }\mathrm{,}}\hfill \\ \hfill {\displaystyle {\left(5\mathrm{,}24x\right)}^2}& {\displaystyle ={\left(2x\right)}^2+25-2\cdot 2x\cdot 5\cdot \left(-0\mathrm{,}5\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle 27\mathrm{,}4576x^2}& {\displaystyle =4x^2+25+10x\mathrm{,}}\hfill \\ \hfill {\displaystyle 23\mathrm{,}4576x^2}& {\displaystyle -10x-25=0.}\hfill \end{array}}$ Ebből: $x_1\approx -0\mathrm{,}841$ (ami nem megoldás, mert a magasság csak pozitív lehet), $x_2\approx 1\mathrm{,}267$. Tehát a hegy 1267 méter magas.     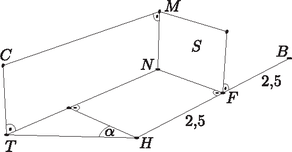$b)$ A madár ($M$) rajta van a $HB$ szakasz $S$ felezőmerőleges síkján, a hegy csúcsának magasságában. Helyzetét az ábra szemlélteti. A keresett távolság $MC$, ennek a vízszintes szakasznak a vízszintes síkra eső merőleges vetülete $TN$, és ez a $TNFH$ derékszögű trapéz hosszabbik alapja lesz. A $TP$ szakasz hosszát a $TPH$ derékszögű háromszögben számítjuk ki. A látószögek felhasználásával a $THC$ és a $TBC$ derékszögű háromszögekben: $\begin{array}{c}{\displaystyle TH=\frac{x}{\text{tg}{30}^{\circ }}\approx 2\mathrm{,}195\text{és}TB=\frac{x}{\text{tg}{11}^{\circ }}\approx 6\mathrm{,}518.}\end{array}$ A $THB$ háromszögben a koszinusztétel alapján: $\begin{array}{c}{\displaystyle 6\mathrm{,}{518}^2=2\mathrm{,}{195}^2+5^2-2\cdot 5\cdot 2\mathrm{,}195\cdot \text{cos}\left(\alpha +{90}^{\circ }\right)\mathrm{,}}\end{array}$ ebből $\text{cos}\left(\alpha +{90}^{\circ }\right)\approx -0\mathrm{,}5771$, azaz $\alpha +{90}^{\circ }\approx 125\mathrm{,}{25}^{\circ }$, vagyis $\alpha =35\mathrm{,}{25}^{\circ }$, továbbá a $TPH$ háromszögben $TP=TH\cdot \text{sin}\alpha =2\mathrm{,}195\cdot 0\mathrm{,}5771\approx 1\mathrm{,}267$, $TN=TP+PN=1\mathrm{,}267+2\mathrm{,}5=3\mathrm{,}767$. Tehát a madár a hegycsúcsot 3767 méterre közelítheti meg.