Cím:	Megoldásvázlatok a 2011/2. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Számadó László
Füzet:	2011/március, 144 - 150. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldásvázlatok a 2011/2. sz. emelt szintű gyakorló feladataihoz   I. rész     1. Oldjuk meg a következő egyenletet: $\begin{array}{c}{\displaystyle \left(x-\sqrt[]{x-5}-5\right)\left(x^2-11x+28\right)=0.}\end{array}$  (14 pont)   Megoldás. Értelmezési tartomány: $x\ge 5$. Az egyenlet a következő alakra hozható: $\begin{array}{c}{\displaystyle \left(x-4\right)\cdot \sqrt[]{x-5}\cdot \left(\sqrt[]{x-5}-1\right)\left(x-7\right)=0.}\end{array}$ Egy szorzat akkor nulla, ha legalább egy tényezője nulla. A négy tényező rendre a 4, 5, 6, 7 helyen lesz nulla. Az értelmezési tartományt figyelembe véve az egyenlet megoldásai: $x_1=5$, $x_2=6$, $x_3=7$.   2. Veronika egy olyan programot írt a számítógépre, amely egy pozitív egész számot kér bemenő adatként, majd egy billentyű megnyomására a soron következő egész számmal megnövelt összeg lesz látható a képernyőn. A billentyű újabb megnyomásával mindig az utolsónak kapott összeget növeli a gép, $1$-gyel nagyobb számmal, mint az ezt megelőző lépésben, és az így kapott összeg megjelenik a képernyőn. Egyik alkalommal az $59$. billentyűnyomás után a $2010$ jelent meg a képernyőn. Melyik szám volt ekkor a bemenő adat? $\begin{array}{c}\end{array}$ (12 pont)   Megoldás. Legyen a bemenő adat az $x$. Az első billentyűnyomás utáni összeg $x+\left(x+1\right)$, az 59. után pedig $x+\left(x+1\right)+\text{...}+\left(x+59\right)$. Ez egy számtani sorozat egymást követő hatvan tagjának az összege. A sorozat első tagja $x$, differenciája 1, az összege 2010. Vagyis: $\begin{array}{c}{\displaystyle S_{60}=\frac{60}{2}\left[2x+\left(60-1\right)\cdot 1\right]=30\left(2x+59\right)=2010.}\end{array}$ Ebből kapjuk, hogy $x=4$. Tehát a 4-es volt a bemenő adat. (Valóban: $4+5+6+\text{...}+62+63=2010$).   3. A 2 500 000 Ft-os összeg egyik része egy év alatt 60 000 Ft-ot, a másik része 75 000 Ft-ot kamatozott. Ez utóbbi kamatlába $1\%$-kal kisebb volt, mint az elsőé. Hány százalékos kamatra és mekkora összegeket kötöttünk le?  (14 pont)   Megoldás. Az első lekötés kamatlába legyen $p\%$, ekkor a másik részé $\left(p-1\right)\%$. Az első lekötött rész nagysága: $\begin{array}{c}{\displaystyle \frac{60000}{\frac{p}{100}}=\frac{6000000}{p}\mathrm{.}}\end{array}$ A második lekötött rész nagysága: $\begin{array}{c}{\displaystyle \frac{75000}{\frac{p-1}{100}}=\frac{7500000}{p-1}\mathrm{.}}\end{array}$ A két rész összege adott, ezért felírhatjuk a következő egyenletet: $\begin{array}{c}{\displaystyle \frac{6000000}{p}+\frac{7500000}{p-1}=2500000.}\end{array}$ Az egyenlet mindkét oldalát szorozzuk meg $\frac{p\left(p-1\right)}{500000}$-del: $\begin{array}{c}{\displaystyle 12\left(p-1\right)+15p=5p\left(p-1\right)\mathrm{.}}\end{array}$ A beszorzások, rendezések után a következő másodfokú egyenlethez jutunk: ${\displaystyle \begin{array}{c}\hfill {\displaystyle 5p^2-32p+12=\mathrm{0,}}\hfill \\ \hfill {\displaystyle p_{1;2}=\frac{32\pm \sqrt[]{{32}^2-240}}{10}=\frac{32\pm 28}{10}\mathrm{,}{p}_1=\mathrm{6,}{p}_2=0\mathrm{,}4.}\hfill \end{array}}$ A $p_2$ nem megoldás, hiszen ekkor a $p-1$ negatív lenne. Vagyis 6%-os és 5%-os lekötéseink voltak. Az első lekötött rész: $\begin{array}{c}{\displaystyle \frac{6000000}{p}=\frac{6000000}{6}=1000000.}\end{array}$ A második lekötött rész: $\begin{array}{c}{\displaystyle \frac{7500000}{p-1}=\frac{7500000}{5}=1500000.}\end{array}$ Tehát 1 000 000 Ft volt 6%-os és 1 500 000 Ft pedig 5%-os éves lekötésen. 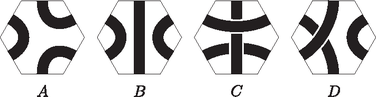(Ezek éves kamata valóban 60 000 Ft, illetve 75 000 Ft.)   4. Egy játék szabályos hatszög alakú lapkákból áll, melyeknek egyik oldalán három különböző színű vonal látható. Egy készlethez négy színt használnak. A vonalak elrendezése alapján négyféle lapka lehetséges, ezeket az ábra mutatja (februári számunk címlapján is).     Hány elemű egy készlet, ha az összes lehetséges lapkából egyet tartalmaz?  (14 pont)   Megoldás. Az $A$ típusú lapkát kétféleképpen színezhetjük. Az egyik szín helyét rögzítjük (legyen ez például a hatszög bal oldalán), a másik kettő helye felcserélhető.     A $B$ típusú lapkát háromféleképpen színezhetjük. Az egyenes vonalat lehet mind a három színnel színezni, de a másik két vonal színét már hiába cseréljük fel, nem kapunk új elrendezést (forgatással egymásba forgathatók).     A $C$ típusú lapkát is háromféleképpen színezhetjük1, hasonlóan az előzőekben elmondottakhoz.     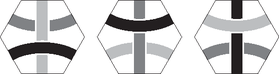A $D$ típusú lapkát hatféleképpen színezhetjük${}^1$. A kis ívet színezhetjük mindhárom színnel, és a másik két ív színeinek felcserélésével új elrendezést kapunk.     Ez eddig 14 darab. Négy színt használhatunk, és négyből hármat kiválasztani négyféleképpen lehet. Bármelyik három szín esetén 14 darab különböző lapka készíthető, így a teljes készlet ennek a négyszerese lesz. Vagyis a készlet 56 darabból áll.   II. rész     5. Egy háromszög két oldalának hossza egész szám. Ha közülük a rövidebbet növeljük $2$-vel, a hosszabbat csökkentjük $2$-vel, az általuk közrezárt szöget pedig változatlanul hagyjuk, akkor a háromszög területe az eredeti terület másfélszerese lesz. Milyen hosszú volt az eredeti háromszög két oldala?  (16 pont)   Megoldás. Legyen a háromszög két oldalhosszának mérőszáma $a$ és $b$ ($a$, $b$ pozitív egész, valamint $a>b$), az általuk közbezárt szög a szokásos jelöléssel $\gamma$. Ekkor a háromszög területe: $t_1=\frac{ab\text{sin}\gamma }{2}$. A megváltoztatott oldalú háromszög területe: $\begin{array}{c}{\displaystyle t_2=\frac{\left(a-2\right)\left(b+2\right)\text{sin}\gamma }{2}\mathrm{.}}\end{array}$ A feladat szövege szerint a megváltoztatott oldalakkal kapott háromszög területe másfélszerese lett az eredeti háromszög területének, ezért: $\begin{array}{c}{\displaystyle \frac{ab\text{sin}\gamma }{2}=\frac{2}{3}\cdot \frac{\left(a-2\right)\left(b+2\right)\text{sin}\gamma }{2}\mathrm{.}}\end{array}$ Ebből kapjuk: $3ab=2\left(a-2\right)\left(b+2\right)$. A beszorzás és rendezés után: $ab-4a+4b+8=0$. Fejezzük ki a $b$-t: $\begin{array}{c}{\displaystyle b=\frac{4a-8}{a+4}=\frac{4\left(a+4\right)-24}{a+4}=4-\frac{24}{a+4}\mathrm{.}}\end{array}$ Az $a+4$ a 24 egész osztója kell, hogy legyen. Ilyen egész szám 16 darab van. Az esetek számának csökkentése érdekében az előző eredményünket így is íratjuk: $\left(a+4\right)\left(b-4\right)=-24$. Mivel $a>b$, ezért $a+4>b-4$. A szorzat csak úgy lehet negatív, hogy az $\left(a+4\right)$-es tényező a 24 pozitív osztója. Tudjuk, hogy az $a-2$ a megváltoztatott oldalú háromszög egyik oldala, így még ennek is pozitívnak kell lenni. Vagyis az $a+4$ a 24, 12, 8, 6, 4, 3, 2, 1 lehetőségek közül csak ez első három lehet. Így kapjuk $a$-ra a 20, 8, 4 értékeket. Ezekhez visszahelyettesítéssel $b$ is számolható. Három megoldást kaptunk:  ${\displaystyle \begin{array}{cc}{\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>20</mn></math>,}}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>b</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>3</mn></math>,}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>8</mn></math>,}}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>b</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>2</mn></math>,}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>3</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>4</mn></math>,}}\hfill & {\displaystyle \text{ <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>b</mi></mrow><mrow><mn>3</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>1</mn></math>. }}\hfill \end{array}}$ Könnyen ellenőrizhető, hogy mindhárom valóban eleget tesz a feladat feltételeinek.   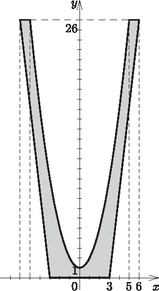6. Egy üvegváza tengelymetszetét koordinátarendszerben ábrázoltuk, melynek egységeit vegyük $1\text{ cm}$ -nek. A forgástest belső felületét az $f\left(x\right)=x^2+1$, a külső felületét a $g\left(x\right)=\frac{26}{3}x-26$ hozzárendelésű függvény $y$  tengely körüli megforgatásával kapjuk. A test magassága $26\text{ cm}$. $a)$ Hány liter víz önthető a vázába anélkül, hogy kicsordulna? $b)$ Mekkora a váza tömege, ha az üveg sűrűsége $2\mathrm{,}6\frac{\text{g}}{{\text{cm}}^3}$?  (16 pont)     Megoldás. $a)$ A váza belső térfogata azonos lesz annak a testnek a térfogatával, amelyet a $h\left(x\right)=\sqrt[]{x}$ hozzárendelésű függvény $x$ tengely körüli megforgatásával kapunk a $\left[0;25\right]$ intervallumon: $\begin{array}{c}{\displaystyle V_1=\pi \underset{0}{\overset{25}{\int }}{\left(\sqrt[]{x}\right)}^{2}dx=\pi \underset{0}{\overset{25}{\int }}xdx=\pi \cdot {\left[\frac{x^2}{2}\right]}_0^{25}=\pi \left(\frac{{25}^2}{2}-\frac{0^2}{2}\right)=312\mathrm{,}5\cdot \pi \approx 982.}\end{array}$     A belső térfogat kb. 982 cm${}^3$, vagyis 0,982 liter víz önthető a vázába. $b)$ A váza alakja csonkakúp, melynek $m$ magassága 26 cm, az alapkör $R$ sugara 3 cm, a fedőkör $r$ sugara 6 cm. A csonkakúp térfogata: $\begin{array}{c}{\displaystyle V_2=\frac{\pi }{3}m\left(R^2+r^2+Rr\right)=\frac{\pi }{3}\cdot 26\cdot \left(3^2+6^2+3\cdot 6\right)=\frac{\pi }{3}\cdot 26\cdot 63=546\pi \mathrm{.}}\end{array}$ Az üveg térfogata cm${}^3$-ben: $\begin{array}{c}{\displaystyle V=V_2-V_1=546\pi -312\mathrm{,}5\pi =233\mathrm{,}5\pi \approx 733\mathrm{,}6.}\end{array}$ Az üveg sűrűsége: $2\mathrm{,}6\frac{\text{g}}{{\text{cm}}^3}$. Az üvegváza tömegét megkapjuk, ha a térfogat és a sűrűség szorzatát vesszük: $\begin{array}{c}{\displaystyle 733\mathrm{,}6\cdot 2\mathrm{,}6=1907\mathrm{,}36.}\end{array}$ Vagyis az üvegváza kb. 1,9 kg tömegű.   7. Igazoljuk, hogy a $8x^3-6x+1=0$ harmadfokú egyenletnek három különböző gyöke van, és ezek egyike a $\text{sin}\frac{\pi }{18}$.  (16 pont)   Megoldás. Vizsgáljuk a minden valós számra értelmezett és mindenütt folytonos $f\left(x\right)=8x^3-6x+1$ hozzárendeléssel megadott függvényt. Mivel az $f\text{'}\left(x\right)=24x^2-6$ függvény zérushelyei a $-\frac{1}{2}$ és az $\frac{1}{2}$, ezért itt lehet az eredeti függvénynek lokális szélsőértéke. Ezeken a helyeken az első derivált előjelet vált (pozitívból negatívba, illetve negatívból pozitívba megy át), így az első helyen lokális maximuma, a második helyen lokális minimuma van a függvénynek. Számolással kapjuk, hogy $f\left(-0\mathrm{,}5\right)=3$ és $f\left(0\mathrm{,}5\right)=-1$. Vagyis a $]-\frac{1}{2};\frac{1}{2}[$ intervallumon a függvénynek zérushelye van. Mivel $\underset{x\to \infty }{\overset{}{\text{lim}}}\left(8x^3-6x-1\right)=\infty$, azért a $]\frac{1}{2};\infty [$ intervallumon is van a függvénynek zérushelye. Mivel $\underset{x\to -\infty }{\overset{}{\text{lim}}}\left(8x^3-6x-1\right)=-\infty$, azért a $]-\infty ;-\frac{1}{2}]$ intervallumon is van zérushelye a függvénynek. Ezek alapján a $8x^3-6x+1=0$ harmadfokú egyenletnek valóban három különböző gyöke van. Meg kell még mutatnunk, hogy a $\text{sin}\frac{\pi }{18}$ gyöke a megadott harmadfokú egyenletnek, azaz $\begin{array}{c}{\displaystyle 8\text{sin}{}^3\frac{\pi }{18}-6\text{sin}\frac{\pi }{18}+1=0.}\end{array}$ A $\frac{\pi }{18}$ háromszorosa $\frac{\pi }{6}$, ami nevezetes szög, és tudjuk, hogy $\text{sin}\frac{\pi }{6}=\frac{1}{2}$. Alkalmazzuk a $\text{sin}3\alpha =3\text{sin}\alpha -4\text{sin}{}^3\alpha$ összefüggést: $\begin{array}{c}{\displaystyle \text{sin}\frac{\pi }{6}=3\text{sin}\frac{\pi }{18}-4\text{sin}{}^3\frac{\pi }{18}\mathrm{.}}\end{array}$ Ezt 2-vel szorozva és rendezve kapjuk: $\begin{array}{c}{\displaystyle 8\text{sin}{}^3\frac{\pi }{18}-6\text{sin}\frac{\pi }{18}+1=0.}\end{array}$ Vagyis a megadott harmadfokú egyenlet egyik gyöke valóban a $\text{sin}\frac{\pi }{18}$.   8. Adott három kör az egyenletével: $x^2+10x+y^2-6y+30=0$, $x^2+4x+y^2+2y+4=0$, $x^2-14x+y^2+4y+44=0$. $a)$ Mekkora a középpontjaik által meghatározott háromszög kerülete? $b)$ Igazoljuk, hogy ennek a háromszögnek a területe racionális szám. $c)$ Adjuk meg annak a pontnak a koordinátáit, amelytől mindhárom középpont egyenlő távolságra van.  (16 pont)   Megoldás. $a)$ Az körök egyenletét átírhatjuk a következő alakba: $\begin{array}{c}{\displaystyle {\left(x+5\right)}^2+{\left(y-3\right)}^2=\mathrm{4,}{\left(x+2\right)}^2+{\left(y+1\right)}^2=\mathrm{1,}{\left(x-7\right)}^2+{\left(y+2\right)}^2=9.}\end{array}$ A három kör középpontja $A\left(-5;3\right)$, $B\left(-2;-1\right)$, $C\left(7;-2\right)$. Mivel $AB=5$, $BC=\sqrt[]{82}$, $AC=13$, azért a háromszög kerülete: $k=18+\sqrt[]{82}\approx 27\mathrm{,}06$.     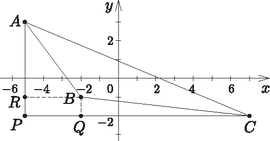$b)$ Az ábrán látható módon rajzoljuk meg az $APC$ derékszögű háromszöget az $ABC$ háromszöghöz. Az ábra jelöléseit és a rendelkezésünkre álló adatokat használva: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle t_{ABC}}& {\displaystyle =t_{APC}-t_{ARB}-t_{RPQB}-t_{BQC}=\frac{5\cdot 12}{2}-\frac{4\cdot 3}{2}-1\cdot 3-\frac{1\cdot 9}{2}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =30-6-3-4\mathrm{,}5=16\mathrm{,}5.}\hfill \end{array}}$ Vagyis az $ABC$ háromszög területe racionális szám. $c)$ A keresett pont az $ABC$ háromszög köré írt körének a középpontja lesz. Ezt a pontot kapjuk például az $AB$ és az $AC$ oldalak felezőmerőlegeseinek metszéspontjaként. Az $AB$ oldal felezőpontja: $F_3(-\frac{7}{2};1)$, a felezőmerőleges egy normálvektora: $\overrightarrow{n_3}\left(3;-4\right)$. A felezőmerőleges egyenlete: $f_3:3x-4y=-14\mathrm{,}5$. Az $AC$ oldal felezőpontja: $F_2(1;\frac{1}{2})$, a felezőmerőleges egy normálvektora: $\overrightarrow{n_2}\left(12;-5\right)$. A felezőmerőleges egyenlete: $f_2:12x-5y=9\mathrm{,}5$. A két egyenletből megkapjuk a keresett pont koordinátáit: $x=\frac{221}{66}$, $y=\frac{135}{22}$.   Tehát a $(\frac{221}{66};\frac{135}{22})$ ponttól mindhárom középpont azonos távolságra van.   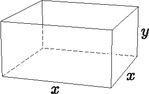9. Egy felülről nyitott négyzet alapú, $4{\text{dm}}^2$ felszínű dobozt szeretnénk készíteni, amelynek a lehető legnagyobb a térfogata. Adjuk meg a doboz maximális térfogatának pontos értékét. Mekkora a doboz éleinek hossza milliméter pontossággal?  (16 pont)   Megoldás. Legyen a doboz alaplapjának éle $x$, a magassága $y$ hosszúságú. Ekkor a doboz felszíne: $A=x^2+4xy=4$, térfogata: $V=x^{2}y$. A felszín adta összefüggésből: $\begin{array}{c}{\displaystyle y=\frac{4-x^2}{4x}\mathrm{.}}\end{array}$     Ezt beírva a $V$ képletébe látható, hogy a doboz térfogata csak $x$-től függ, azaz: $\begin{array}{c}{\displaystyle V\left(x\right)=x^2\cdot \frac{4-x^2}{4x}=x-\frac{1}{4}{x}^3\mathrm{.}}\end{array}$ Vizsgáljuk meg a $V\left(x\right)$ függvényt a maximumhelyek szempontjából. Deriváljuk a függvényt: $V\text{'}\left(x\right)=1-\frac{3}{4}{x}^2$. A derivált zérushelyei: $\begin{array}{c}{\displaystyle x_1=-\frac{2}{\sqrt[]{3}}\mathrm{,}{x}_2=\frac{2}{\sqrt[]{3}}\mathrm{.}}\end{array}$ A negatív gyök a feladatban nem jöhet szóba, mert az $x$ távolságot jelölt, így a $V\left(x\right)$ függvényt a pozitív értékekre leszűkítve vizsgáljuk. Tudjuk, hogy egy függvénynek ott lehet szélsőértéke, ahol a deriváltja nulla. Meg kell még állapítanunk, hogy az $x_2$ helyen valóban van-e szélsőértéke a $V\left(x\right)$ függvénynek, és hogy az maximum-e. Vizsgálatunk részletei a következő táblázatban láthatók:   ${\displaystyle \begin{array}{|cccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn><mo stretchy="false"><</mo><mi>x</mi><mo stretchy="false"><</mo><mrow><mfrac><mrow><mn>2</mn></mrow><mrow><mrow><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot></mrow></mrow></mfrac></mrow></math> <math xmlns="http://www.w3.org/1998/Math/MathML"><mspace backround="\#000" height="14pt" depth="12pt" width="0pt"></mspace></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi><mo stretchy="false">=</mo><mrow><mfrac><mrow><mn>2</mn></mrow><mrow><mrow><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot></mrow></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>2</mn></mrow><mrow><mrow><mroot><mrow><mn>3</mn></mrow><mrow></mrow></mroot></mrow></mrow></mfrac></mrow><mo stretchy="false"><</mo><mi>x</mi></math> }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>V</mi><mo stretchy="false">'</mo><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>x</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">+</mo></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo></math> }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>V</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>x</mi></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>↗</mo></math>}}\hfill & \hfill {\displaystyle \text{maximum}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>↘</mo></math> }}\hfill \\ \hline\end{array}}$   Vagyis az $x=\frac{2}{\sqrt[]{3}}$ valóban maximumhelye a függvénynek. Ennek ismeretében az $y$ is meghatározható: $\begin{array}{c}{\displaystyle y=\frac{4-x^2}{4x}=\frac{4-(\frac{2}{\sqrt[]{3}}{)}^2}{4\cdot \frac{2}{\sqrt[]{3}}}=\frac{\frac{8}{3}}{\frac{8}{\sqrt[]{3}}}=\frac{\sqrt[]{3}}{3}\mathrm{.}}\end{array}$ A maximális térfogat pontos értéke dm${}^3$-ben: $\begin{array}{c}{\displaystyle V=x^{2}y={\left(\frac{2}{\sqrt[]{3}}\right)}^2\cdot \frac{\sqrt[]{3}}{3}=\frac{4\sqrt[]{3}}{9}\mathrm{.}}\end{array}$ Az eddigi számításainkban szereplő hosszúságokat deciméterben adtuk meg, ezért az $x$ és $y$ értékét két tizedes jegyre kell kerekítenünk, hogy milliméter pontosságot   kapjunk. Vagyis: $x=\frac{2}{\sqrt[]{3}}\approx 1\mathrm{,}15$, $y=\frac{\sqrt[]{3}}{3}\approx 0\mathrm{,}58$, vegyük észre, hogy $x=2y$.   Azaz a feladatban szereplő maximális térfogatú doboz alaplapjának éle milliméterre kerekítve 115 mm, a magassága pedig 58 mm.   ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-weight: bold;">Számadó László</span>}}\hfill \end{array}}$   ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{Budapest}}\hfill \end{array}}$ 1Eltekintünk attól, hogy melyik vonal van alul, illetve fölül. Ha ettől nem tekintenénk el, akkor a $C$ esetben is és a $D$ esetben is kétszer ennyi lehetőségünk lenne. A tantrix játékban sem lényeges, hogy melyik vonal van alul, illetve fölül.