Cím:	Nyomozás a Spirál-családban
Szerző(k):	Halász Ágnes
Füzet:	2011/március, 130 - 139. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Nyomozás a Spirál-családban     1. Bevezetés Ezen cikk a spirálok világában való eligazodásban nyújthat segítséget: megkísérli kitisztítani a néhol hallható és olvasható fogalomzavarokat, a felületességből eredő homályos, összemosó, sőt hibás kijelentéseket. Kalandra hívja az olvasót: rendszerezzük mind történetileg, mind matematikailag a legfontosabb spirálokat, és ‐ ha kedvünk van hozzá ‐ találjunk ki magunk is hasonlót, vagy leljünk örömet megrajzolásukban, szerkesztésükben. Végül ‐ legmélyebben fekvő ,,szeletként'' ‐ fényt derítünk a címben ígért rokonságra.   2. A kezdetek A kozmosz legősibb megjelenítése (például a hinduizmusban vagy egyes indián törzseknél) különböző alakzatokkal történt (1. ábra).     1. ábra   Mindkettőnél a ,,nem látható'' közép a lényeget, a bármeddig tágíthatóság pedig a világegyetem végtelenérzetét jelképezi. Geometriailag azonban lényegesen különböznek egymástól. Az 1. ábra jobboldali alakzata nem koncentrikus körökből áll, hanem spirál: síkbeli folytonos görbe. 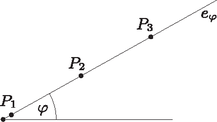Nemcsak szimbólumként, hanem a matematikai megközelíthetőség tárgyaként is vissza-visszatérnek az évszázadok során a spirálok. Kr.e. 225-ből való Arkhimédész leírása arról a fajta spirálról, amely azóta is az ő nevét viseli. Mai terminológiát használva az arkhimédészi spirál egy polárkoordinátákkal megadott egyenlettel meghatározott görbe: $\begin{array}{c}{\displaystyle r=a\phi \mathrm{,}}\end{array}$ ahol $r$ a kiinduló ponttól (origótól) mért távolság; $\phi$ az elfordulás szöge (az $x$-tengely pozitív felével bezárt forgásszög); $a$ tetszőleges pozitív állandó, amely a spirál jellegét (sűrűségét) határozza meg.   $P_1\left(r_1;\phi \right)$, $P_2\left(r_2;\phi +2\pi \right)$, $P_n\left(r_n;\phi +\left(n-1\right)2\pi \right)$, $\text{...}$, ahol $r_i=a\left[\phi +\left(i-1\right)2\pi \right]$   Az Arkhimédész-féle spirál ágai közti távolság az $a$ értékétől függő állandó. (Minél kisebb az $a\ne 0$ értéke, annál sűrűbbek az ágai.) Ugyanis: $\begin{array}{c}{\displaystyle r_n-r_{n-1}=a\left[\phi +\left(n-1\right)2\pi \right]-a\left[\phi +\left(n-2\right)2\pi \right]=2a\pi \mathrm{.}}\end{array}$   Szabadkézzel úgy rajzolhatjuk meg, hogy az első körben minél több értéket kiszámítva, kialakítjuk a kezdő formát, majd az $e_{\phi }$ félegyenesekre a $2a\pi$ közelítő értékének megfelelő távolságot $P_1$-től kezdve felmérjük. Az így kapott spirálpontokat összekötjük.   2. ábra   A 2. ábrán a szürkével rajzolt spirálnál $a=\frac{1}{2}$, a feketénél $a=\frac{1}{4}$. Így az ágak közti távolság az alábbi, a rajzolást segítő táblázat utolsó oszlopában megjelenő érték:   ${\displaystyle \begin{array}{|ccccccccccccccc|}\hline {\displaystyle }\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>φ</mi></math>}}& {\displaystyle \text{ 0}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>π</mi></mrow><mrow><mn>6</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>π</mi></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>π</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>2</mn><mi>π</mi></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>5</mn><mi>π</mi></mrow><mrow><mn>6</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>π</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>7</mn><mi>π</mi></mrow><mrow><mn>6</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>4</mn><mi>π</mi></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>3</mn><mi>π</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>5</mn><mi>π</mi></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>11</mn><mi>π</mi></mrow><mrow><mn>6</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{ 2<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>π</mi></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mspace backround="\#000" depth="7pt" width="0pt"></mspace></math>}}\hfill \\ {\displaystyle \text{szürke:}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>r</mi><mo stretchy="false">=</mo><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></mrow><mi>φ</mi></math>}}& {\displaystyle \text{ 0}}\hfill & \hfill {\displaystyle \text{ 0,3}}\hfill & \hfill {\displaystyle \text{ 0,5}}\hfill & \hfill {\displaystyle \text{ 0,8}}\hfill & \hfill {\displaystyle \text{ 1}}\hfill & \hfill {\displaystyle \text{ 1,3}}\hfill & \hfill {\displaystyle \text{ 1,5}}\hfill & \hfill {\displaystyle \text{ 1,8}}\hfill & \hfill {\displaystyle \text{ 2,1}}\hfill & \hfill {\displaystyle \text{ 2,3}}\hfill & \hfill {\displaystyle \text{ 2,6}}\hfill & \hfill {\displaystyle \text{ 2,8}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">3,1</span> }}\hfill \\ {\displaystyle \text{fekete:}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>r</mi><mo stretchy="false">=</mo><mrow><mfrac><mrow><mn>1</mn></mrow><mrow><mn>4</mn></mrow></mfrac></mrow><mi>φ</mi></math>}}& {\displaystyle \text{ 0}}\hfill & \hfill {\displaystyle \text{ 0,1}}\hfill & \hfill {\displaystyle \text{ 0,3}}\hfill & \hfill {\displaystyle \text{ 0,4}}\hfill & \hfill {\displaystyle \text{ 0,5}}\hfill & \hfill {\displaystyle \text{ 0,7}}\hfill & \hfill {\displaystyle \text{ 0,8}}\hfill & \hfill {\displaystyle \text{ 0,9}}\hfill & \hfill {\displaystyle \text{ 1}}\hfill & \hfill {\displaystyle \text{ 1,1}}\hfill & \hfill {\displaystyle \text{ 1,3}}\hfill & \hfill {\displaystyle \text{ 1,4}}\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">1,6</span> }}\hfill \\ \hline\end{array}}$   Ezt a görbét közelítő értékekkel felvett véges sok pont szabadkézi összekötésével rajzoltuk meg, így ‐ természetesen ‐ euklidészi szerkesztésről nem beszélhetünk.   3. Szerkesszünk spirált! 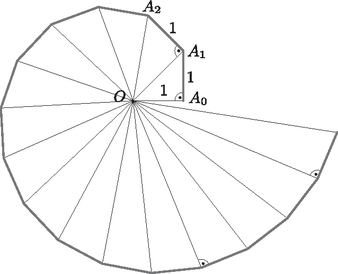3.a. Spirált pontosan is szerkeszthetünk. Szakaszokból áll a rekurzív-módon megadott ún. négyzetgyök-spirál. Induljunk ki egy egyenlő szárú derékszögű háromszögből (3. ábra): $O{A}_0{A}_1▵$, amelyben $O{A}_0=A_0{A}_1=1$ egység. Majd illesszük hozzá az $O{A}_1{A}_2$ derékszögű háromszöget, amelyben $A_1{A}_2=1$ egység. Ez az eljárás bármeddig folytatható. Legyen $O{A}_i=a_i$, ekkor $a_i^2=a_{i-1}^2+1$.     3. ábra   Nevét onnan kapta, hogy igaz rá az a tulajdonság, hogy $a_{n-1}=\sqrt[]{n}$, azaz bármely természetes szám négyzetgyökének megfelelő hosszúságú szakaszt ‐ elvileg ‐ megszerkeszthetünk ezzel a módszerrel. A bizonyítás teljes indukcióval könnyen elvégezhető: $a_0=1$ és $a_1=\sqrt[]{1+1}=\sqrt[]{2}$. Tegyük fel, hogy $a_{k-2}=\sqrt[]{k-1}$. 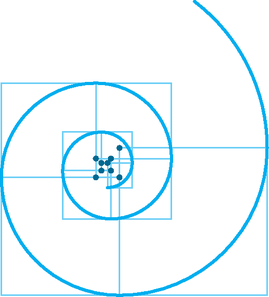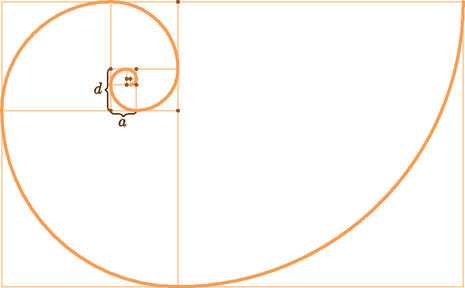Ekkor $\begin{array}{c}{\displaystyle {\left(a_{k-1}\right)}^2={\left(a_{k-2}\right)}^2+1=k-1+1=k\mathrm{,}\text{tehát}{a}_{k-1}=\sqrt[]{k}\mathrm{.}}\end{array}$   3.b. Szakaszok helyett körívekből is létrehozhatunk pontosan szerkeszthető spirált. Kiindulásul válasszunk egy négyzetet vagy egy egyenlőszárú (nem derékszögű) háromszöget és egy $q>1$ valós számot (4. ábra).     4.a. ábra. $q=2$     4.b. ábra. $q=\frac{5}{4}$     4.c. ábra. $q=\frac{1+\sqrt[]{5}}{2}$     4.d. ábra. 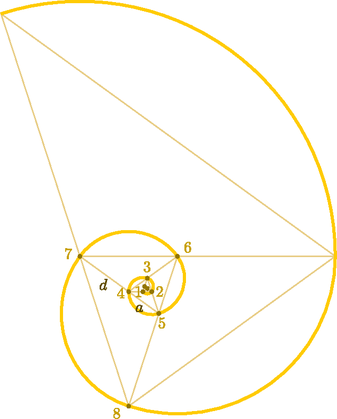A háromszög szárszöge ${60}^{\circ }$ és $q=\frac{3}{2}$     4.e. ábra. A háromszög szárszöge ${108}^{\circ }$ és $q=\frac{1+\sqrt[]{5}}{2}$   A 4. ábra mindegyik spiráljánál a körívek sugarai $q$ hányadosú mértani sorozatot alkotnak. Kitüntetett szerepű a 4.c. és az 4.e. ,,aranyspirál'', ahol a körsugarak $a$, $d$, $a+d$, $a+2d$, $2a+3d$, $\text{...}$ szabály szerint követik egymást (ún. Fibonacci-sorozat, amelyben $f_n=f_{n-2}+f_{n-1}$). Ez utóbbi spirálok ‐ a mértani közép tulajdonság miatt ‐ ,,gyorsan táguló'' formájúak.   3.c. ''Gyorsan örvénylő'' spirált rajzolhatunk, ha az Arkhimédész-féle $\frac{r}{\phi }=\text{állandó}$   szabályt $r\phi =\text{állandóra}$ változtatjuk. Az $r\phi =a$ polárkoordinátás egyenlettel megadott alakzatot ‐ természetesen ‐ ismét csak közelítő módszerrel vázolhatjuk fel (5. ábra, $a=1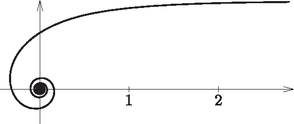$).   5. ábra   Az 5. ábrán látható spirálnak nem lehet kezdőpontja, hiszen $r\ne 0$, és $\phi \to \infty$ esetén megfelelő pontjai egyre közelebb kerülnek az origóhoz. Ez indokolja a hiperbolikus spirál elnevezését. Hasonló jellegű, de kettős spirál rajzolható, ha $r=\frac{a}{\phi }$   helyett az $r^2=\frac{a^2}{\phi }$ egyenletből indulunk ki (6. ábra, $a^2=1$).     6. ábra   A csavarodó, majd kissé hajlottan elnyúló forma emlékeztet a római madárjósok görbe botjára, a ,,lituus''-ra. Innen kapta ez a fajta spirál a lituus nevet.   4. Fermat és Descartes 4.a. A 17. század elején élt Toulouse-ban egy jogász, aki minden idejét és energiáját a matematikának szentelte: az újabb és újabb kérdések izgalma és a gondolkodás élvezete hajtotta. Pierre Fermat jogtanácsos nem mozdult ki városából, nem publikálta tételeit, feljegyzései és levelei maradtak fenn csak. Pascallal valószínűségi problémákról, Descartes-tal pedig az algebra és a geometria egyesítésével kapcsolatos gondolatairól ‐ az analitikus geometriáról ‐ levelezett. Ezekből a levélváltásokból született meg a matematika két új fejezete. Fermat a ,,legzseniálisabb amatőr''-ként él a matematika történetében. Nevét, többek között, egy általa kidolgozott spirál is őrzi. 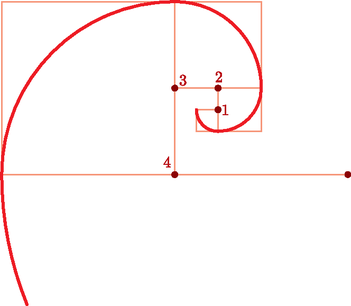A Fermat-féle spirál az archimédészi-ből képez új kettős spirált az $r^2=a^2\phi$ egyenlettel (7. ábra, $a=1$). Ezt a spirált az archimédészi-től eltérően, nem azonos távolságú, hanem ,,lassan sűrűsödő'' ágak alkotják. 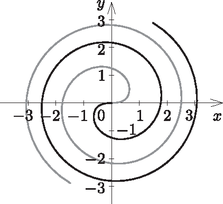  7. ábra   Tekintsük ugyanis a 7. ábrán látható görbének a ${\displaystyle \begin{array}{c}\hfill {\displaystyle P_1\left(r_1;\phi \right)\mathrm{,}{P}_2\left(r_2;\phi +2\pi \right)\mathrm{,}\text{...}\mathrm{,}}\hfill \\ \hfill {\displaystyle P_i\left(r_i;\phi +\left(i-1\right)2\pi \right)}\hfill \end{array}}$ pontjait, ahol $r_i=a\sqrt[]{\phi +\left(i-1\right)2\pi }$. Vizsgáljuk az $\frac{r_{i+1}}{r_i}$ hányadost: $\begin{array}{c}{\displaystyle \frac{r_{i+1}}{r_i}=\sqrt[]{\frac{\phi +i2\pi }{\phi +\left(i-1\right)2\pi }}=\sqrt[]{1+\frac{2\pi }{\phi +\left(i-1\right)2\pi }}\mathrm{.}}\end{array}$ Mivel $i$ értékét növelve a $\frac{2\pi }{\phi +\left(i-1\right)2\pi }$ tört értéke egyre kisebb, azért $\underset{}{\overset{}{\text{lim}}}\frac{r_{i+1}}{r_i}=1$ ($i\to \infty$), ami éppen a sűrűsödést jelenti.   4.b. Descartes ‐ a levelezőtárs ‐ is megalkotta a maga spirálját. Az ő definíciója azonban alapvetően különbözik az összes eddigitől, ahol $r$, illetve $r^2$ és $\phi$ között egyenes- vagy fordított arányosság-jellegű kapcsolat áll fenn. A Descartes-féle spirál egyenlete: ${\displaystyle \begin{array}{c}\hfill {\displaystyle r=a\cdot e^{k\phi }\left(a>0;k\ne 0\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{ln}r=\text{ln}a+k\phi \mathrm{,}}\hfill \\ \hfill {\displaystyle \phi =\frac{1}{k}\text{ln}\frac{r}{a}\mathrm{.}}\hfill \end{array}}$ E sorok indokolttá teszik a logaritmikus spirál elnevezést (8. ábra). 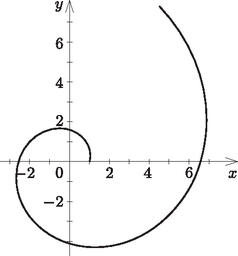  8. ábra   A szabadkézi rajzolást segítő táblázat ($a=1$; $k=\mathrm{0,3}$):   ${\displaystyle \begin{array}{|cccccccccccccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>ϕ</mi></math>}}\hfill & \hfill {\displaystyle \text{ 0}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>π</mi></mrow><mrow><mn>6</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>π</mi></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>π</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>2</mn><mi>π</mi></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>5</mn><mi>π</mi></mrow><mrow><mn>6</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>π</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>7</mn><mi>π</mi></mrow><mrow><mn>6</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>4</mn><mi>π</mi></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>3</mn><mi>π</mi></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>5</mn><mi>π</mi></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>11</mn><mi>π</mi></mrow><mrow><mn>6</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{ 2<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>π</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>13</mn><mi>π</mi></mrow><mrow><mn>6</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>7</mn><mi>π</mi></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></math><math xmlns="http://www.w3.org/1998/Math/MathML"><mspace backround="\#000" depth="7pt" width="0pt"></mspace></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>e</mi></mrow><mrow><mn>0</mn><mn>,</mn><mn>3</mn><mi>ϕ</mi></mrow></msup></mrow></math>}}\hfill & \hfill {\displaystyle \text{ 1}}\hfill & \hfill {\displaystyle \text{ 1,2}}\hfill & \hfill {\displaystyle \text{ 1,4}}\hfill & \hfill {\displaystyle \text{ 1,6}}\hfill & \hfill {\displaystyle \text{ 1,9}}\hfill & \hfill {\displaystyle \text{ 2,2}}\hfill & \hfill {\displaystyle \text{ 2,6}}\hfill & \hfill {\displaystyle \text{ 3}}\hfill & \hfill {\displaystyle \text{ 3,5}}\hfill & \hfill {\displaystyle \text{ 4,1}}\hfill & \hfill {\displaystyle \text{ 4,8}}\hfill & \hfill {\displaystyle \text{ 5,6}}\hfill & \hfill {\displaystyle \text{ 6,6}}\hfill & \hfill {\displaystyle \text{ 7,7}}\hfill & \hfill {\displaystyle \text{9 }}\hfill \\ \hline\end{array}}$   Ha végignézzük az eddigi rajzokat, feltűnik, hogy a 4. ábrán látható spirálfajta ‐ formáját tekintve ‐ közeli rokonságban állhat a logaritmikus spirállal. Izgalmas lehet fényt deríteni e rokoni szálakra, ezért érdemes számba venni a Descartes-féle spirál jellemző tulajdonságait. 1. A görbe derivált görbéje önmagához hasonló: $r\text{'}\left(\phi \right)=ak{e}^{k\phi }=kr\left(\phi \right)$. (Az sem lehetetlen, hogy ez az összefüggés ihlette Descartes-ot e spirál megalkotására.)   2. Az azonos szögelfordulásokhoz tartozó $O{P}_1=r_1$, $O{P}_2=r_2$, $\text{...}$ vezérsugarak mértani sorozatot alkotnak. E sorozat hányadosa: $e^{k\Delta \phi }$. Igazolásként tekintsük az $\frac{r_{n+1}}{r_n}$ hányadost: $\begin{array}{c}{\displaystyle \frac{r_{n+1}}{r_n}=\frac{a{e}^{k{\phi }_{n+1}}}{a{e}^{k{\phi }_n}}=e^{k\Delta \phi }\mathrm{,}}\end{array}$ ahol ${\phi }_1\mathrm{,}{\phi }_2\mathrm{,}\text{...}$ számtani sorozatot képez, melynek differenciája $\Delta \phi$. 3. A görbe bármely pontjába húzott vezérsugár és érintő hajlásszöge állandó. Ha ezt az állandó szöget $\alpha$-val jelöljük, akkor $\text{tg}\alph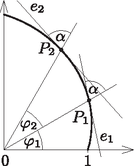a =\frac{1}{k}$ (9. ábra).   9. ábra   A bizonyításhoz térjünk át derékszögű koordinátákra: $\begin{array}{c}{\displaystyle P\left(x;y\right)=P\left(r\left(\phi \right)\text{cos}\phi ;r\left(\phi \right)\text{sin}\phi \right)\mathrm{.}}\end{array}$ Az érintő meredeksége (ha van): $\begin{array}{c}{\displaystyle m_e=\frac{y\text{'}}{x\text{'}}=\frac{r\text{'}\left(\phi \right)\text{sin}\phi +r\left(\phi \right)\text{cos}\phi }{r\text{'}\left(\phi \right)\text{cos}\phi -r\left(\phi \right)\text{sin}\phi }\mathrm{.}}\end{array}$ Az 1. tulajdonság miatt $\begin{array}{c}{\displaystyle m_e=\frac{k\text{sin}\phi +\text{cos}\phi }{k\text{cos}\phi -\text{sin}\phi }\mathrm{.}}\end{array}$ Az $OP$ vezérsugár meredeksége (ha van): $\begin{array}{c}{\displaystyle m_{OP}=\frac{y}{x}=\frac{\text{sin}\phi }{\text{cos}\phi }\mathrm{.}}\end{array}$ A két egyenes hajlásszögének ($\alpha$) meghatározásához használjuk az ismert trigonometrikus összefüggést: $\begin{array}{c}{\displaystyle \text{tg}\alpha =\left|\frac{m_{OP}-m_e}{1+m_{OP}{m}_e}\right|=\left|\frac{\frac{\text{sin}\phi \left(k\text{cos}\phi -\text{sin}\phi \right)-\text{cos}\phi \left(k\text{sin}\phi +\text{cos}\phi \right)}{\text{cos}\phi \left(k\text{cos}\phi -\text{sin}\phi \right)}}{\frac{\text{cos}\phi \left(k\text{cos}\phi -\text{sin}\phi \right)+\text{sin}\phi \left(k\text{sin}\phi +\text{cos}\phi \right)}{\text{cos}\phi \left(k\text{cos}\phi -\text{sin}\phi \right)}}\right|\mathrm{.}}\end{array}$ Elvégezve a kijelölt műveleteket és a lehetséges egyszerűsítéseket: $\begin{array}{c}{\displaystyle \text{tg}\alpha =\left|\frac{-\left(\text{sin}{}^2\phi +\text{cos}{}^2\phi \right)}{k\left(\text{sin}{}^2\phi +\text{cos}{}^2\phi \right)}\right|=\frac{1}{k}\mathrm{.}}\end{array}$   Megjegyzések: 1. Nincs értelmezve az érintő meredeksége, ha $\text{sin}\phi =k\text{cos}\phi$. Ekkor $\alpha ={90}^{\circ }-\phi$, azaz $\text{tg}\alpha =\text{ctg}\phi$, és valóban $\begin{array}{c}{\displaystyle \text{ctg}\phi =\frac{\text{cos}\phi }{\text{sin}\phi }=\frac{1}{k}\mathrm{.}}\end{array}$   2. A vezérsugár meredeksége akkor nincs értelmezve, ha $\text{cos}\phi =0$. Ekkor $\begin{array}{c}{\displaystyle m_e=\frac{k\text{sin}\phi }{-\text{sin}\phi }=-k\mathrm{,}\text{és}\text{tg}\alpha =\frac{1}{-\text{tg}\beta }=\frac{1}{k}\mathrm{.}}\end{array}$   3. A 8. ábrán látható spirál esetén $\begin{array}{c}{\displaystyle \text{tg}\alpha =\frac{10}{3}\mathrm{,}\text{tehát}\alpha \approx {73}^{\circ }\mathrm{.}}\end{array}$   5. Fedezzük fel a rokonságot! Térjünk vissza arra a kérdésre, hogy: Vajon milyen rokonság köti össze a 4. ábra spiráljait a 8. ábrán látható logaritmikus spirállal? A 3. tulajdonság következményeként belátható a következő állítás:   4. Az $r=a\cdot e^{k\phi }$ egyenlettel definiált görbe nem állhat körívdarabokból. A bizonyításhoz használjuk a 10. ábra jelöléseit. Ha feltételezzük, hogy $P_1$ és $P_2$ azonos köríven van, akkor az $e_1$, $e_2$ érintőkre állított $n_1$, $n_2$ merőlegesek $N$ metszéspontja lenne a kör középpontja. De a 3. tulajdonság miatt a $P_1$ és a $P_2$ az $NO$ szakasz (${90}^{\circ }-\alpha$) szögű látókörívének két pontja, mivel $N{P}_{1}O\sphericalangle =N{P}_{2}O\sphericalangle ={90}^{\circ }-\alpha$. E látókör középpontja azonban az $NO$ szakasz felezőmerőlegesén van, tehát nem lehet azonos az $N$ ponttal. Az indirekt feltételezés ellentmondásra vezetett, tehát az állítás igaz. 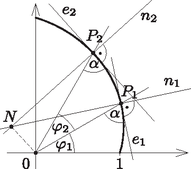  10. ábra   Megjegyzendő még, hogy $\alpha \ne {90}^{\circ }$, (hiszen akkor $\text{ctg}\alpha =0$ lenne, vagyis $k=0$ miatt a spirál elfajulna $a$ sugarú körré), tehát az $N$ és az $O$ pont nem eshet egybe.   5. Ezek után felvetődik a közelíthetőség kérdése. Megközelíthetők-e a spirál-darabok körívekkel? Ha igen, akkor hogyan? Elég jó-e a közelítés? Függ-e $k$-tól? Ha igen, milyen módon? A tengelyeken lévő $P_1$, $P_2$ és $P_3$ spirálpontok (11. ábra) derékszögű háromszög csúcsai. Indoklás: $O{P}_1$; $O{P}_2$ és $O{P}_3$ mértani sorozatot alkotnak. ($q=e^{\frac{k\pi }{2}}>1$). Így $aq=\sqrt[]{a^2{q}^2}$, ami éppen a magasságtétel, tehát $P_1{P}_2{P}_3▵$ derékszögű. 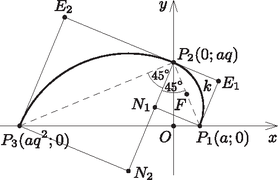  11. ábra   Az 5. megállapítás következménye, hogy:   6. A $P_1{P}_2$ és $P_2{P}_3$ átlójú négyzetek $N_1$ és $N_2$ csúcsa a $P_1{P}_2{P}_3\sphericalangle$ szögfelezőjére esik. Ez a tény biztosítja, hogy a 4.a, b, c. ábra négyzetei $k$-tól függetlenül ráilleszthetők a spirálra (11. ábra). Összehasonlításunk legizgalmasabb állomásához érkeztünk. Az $N_1$ középpontú, $N_1{P}_1$ sugarú $k$ körhöz képest hol helyezkednek el a $P_1{P}_2$ spirálív pontjai? (A 11. ábrát nézve ,,szemléletünk'' teljes egybeesést mutat.) Tekintsük az $N_1{P}_1{E}_1{P}_2$ négyzetet: $\begin{array}{c}{\displaystyle F\left(\frac{a}{2};\frac{aq}{2}\right)\Rightarrow \overrightarrow{F{P}_2}\left(-\frac{a}{2};\frac{aq}{2}\right)\Rightarrow \overrightarrow{F{N}_1}\left(-\frac{aq}{2};-\frac{a}{2}\right)\mathrm{.}}\end{array}$ Ezek szerint a $k$ kör középpontja: $\begin{array}{c}{\displaystyle N_1\left(\frac{a\left(1-q\right)}{2};\frac{a\left(q-1\right)}{2}\right)\mathrm{,}}\end{array}$ sugara: $\begin{array}{c}{\displaystyle \frac{a\sqrt[]{1+q^2}}{\sqrt[]{2}}\mathrm{.}}\end{array}$ A kör egyenlete: $\begin{array}{c}{\displaystyle k:{\left(x-\frac{a\left(1-q\right)}{2}\right)}^2+{\left(y-\frac{a\left(q-1\right)}{2}\right)}^2=\frac{a^2\left(1+q^2\right)}{2}\mathrm{.}}\end{array}$ Átalakítás után: $\begin{array}{c}{\displaystyle x^2+y^2+a\left(q-1\right)\left(x-y\right)=a^{2}q\mathrm{.}}\end{array}$ Behelyettesítve a spirál-pontokat, amelyekre $\begin{array}{c}{\displaystyle x=a\cdot e^{k\phi }\text{cos}\phi \text{és}y=a\cdot e^{k\phi }\text{sin}\phi \mathrm{,}}\end{array}$ azt kapjuk, hogy $\begin{array}{c}{\displaystyle a^2{e}^{2k\phi }+a^2{e}^{k\phi }\left(q-1\right)\left(\text{cos}\phi -\text{sin}\phi \right)=a^{2}q\mathrm{.}}\end{array}$ Elosztva az egyenletet $a^2$-tel, majd átrendezve: $\begin{array}{c}{\displaystyle \left(q-1\right)\left(\text{sin}\phi -\text{cos}\phi \right)=\frac{e^{2k\phi }-q}{e^{k\phi }}\left(\text{ahol }q=e^{\frac{k\pi }{2}}\right)\mathrm{.}}\end{array}$ (1) Ha belátnánk, hogy (1) bal és jobb oldalán álló kifejezés ,,majdnem'' ugyanazokat az értékeket veszi fel a $\phi \in \left[0;\frac{\pi }{2}\right]$ esetben, akkor az azt jelentené, hogy a két vizsgált spirál ,,közelítően'' megegyezik egymással. Mivel $\text{sin}\phi -\text{cos}\phi =\sqrt[]{2}\text{sin}\left(\phi -\frac{\pi }{4}\right)$, azért célszerű bevezetni az $\alpha =\phi -\frac{\pi }{4}$ helyettesítést. Ekkor az (1) bal oldalán álló függvény: $\begin{array}{c}{\displaystyle f\left(\alpha \right)=\sqrt[]{2}\left(e^{\frac{k\pi }{2}}-1\right)\text{sin}\alpha }\end{array}$ az (1) jobb oldalán álló függvény: $\begin{array}{c}{\displaystyle g\left(\alpha \right)=2\frac{e^{k\left(\frac{\pi }{4}+\alpha \right)}-e^{k\left(\frac{\pi }{4}-\alpha \right)}}{2}=2e^{\frac{k\pi }{4}}\text{sinh}\left(k\alpha \right)\left(-\frac{\pi }{4}\le \alpha \le \frac{\pi }{4}\right)\mathrm{.}}\end{array}$ Sőt, az egyes $k$-értékekhez tartozó konstans szorzókat csoportosítva, legyen $\begin{array}{c}{\displaystyle h\left(\alpha \right)=\text{sinh}\left(k\alpha \right)\text{és}j\left(\alpha \right)=\sqrt[]{2}\frac{e^{\frac{k\pi }{2}}-1}{2e^{\frac{k\pi }{4}}}\text{sin}\alpha =\sqrt[]{2}\text{sinh}\left(k\frac{\pi }{4}\right)\text{sin}\alpha \mathrm{.}}\end{array}$ A $h\left(\alpha \right)$ és $j\left(\alpha \right)$ függvények közös tulajdonságai: mindkettő páratlan függvény és $\begin{array}{c}{\displaystyle h\left(\frac{\pi }{4}\right)=j\left(\frac{\pi }{4}\right)\Rightarrow h\left(-\frac{\pi }{4}\right)=j\left(-\frac{\pi }{4}\right)\mathrm{,}\text{valamint}h\left(0\right)=j\left(0\right)\mathrm{.}}\end{array}$ A két függvény ellentétes konvexitású, hiszen $\text{sinh}\text{'}\left(\alpha \right)=\text{cosh}\left(\alpha \right)$ és $\text{sin}\text{'}\left(\alpha \right)=\text{cos}\left(\alpha \right)$, és e két függvény monotonitása a vizsgált intervallumokban ellentétes. Így a $\left[-\frac{\pi }{4};0\right]$-ban $h\left(\alpha \right)$ alulról konkáv, míg $j\left(\alpha \right)$ alulról konvex, a $\left[0;\frac{\pi }{4}\right]$-ben pedig éppen fordítva. Most már felvázolható a két függvény képe.     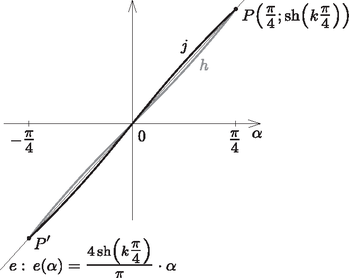12. ábra   Végül becsüljük meg $j$ és $h$ eltérését $e$-től: $\begin{array}{c}{\displaystyle \frac{j\left(\alpha \right)}{e\left(\alpha \right)}=\frac{\sqrt[]{2}\text{sinh}\left(\frac{k\pi }{4}\right)\text{sin}\alpha }{\frac{4\alpha }{\pi }\text{sinh}\left(k\frac{\pi }{4}\right)}=\frac{\sqrt[]{2}\pi }{4}\frac{\text{sin}\alpha }{\alpha }\approx \frac{\pi \sqrt[]{2}}{4}\approx \mathrm{1,}}\end{array}$ mivel ismeretes, hogy $\underset{\alpha \to 0}{\overset{}{\text{lim}}}\frac{\text{sin}\alpha }{\alpha }=1$. $\begin{array}{c}{\displaystyle \frac{e\left(\alpha \right)}{h\left(\alpha \right)}=\frac{\text{sinh}\left(\frac{k\pi }{4}\right)\alpha }{\frac{\pi }{4}\text{sinh}\left(k\alpha \right)}=\frac{\text{sinh}\left(\frac{k\pi }{4}\right)}{\frac{k\pi }{4}}\frac{k\alpha }{\text{sinh}\left(k\alpha \right)}\approx \mathrm{1,}}\end{array}$ mivel $x\to 0$ esetén $\underset{}{\overset{}{\text{lim}}}\frac{\text{sinh}\left(x\right)}{x}=1$. Ezzel beláttuk, hogy az $r\left(\phi \right)=a\cdot e^{k\phi }$ módon definiált logaritmikus spirál közelíthető negyed körívekkel, $a$ és $k$ értékétől függetlenül.     7. Konklúzió Manapság, a könyvesboltok polcain látványos, vonzó kiadványok keresnek rejtett, még fel nem fedezettnek vélt összefüggéseket titokzatos világunkban. Lapozzuk fel egyiket-másikat, és a misztikus következtetések alapjait képező információ-sűrítményt fogadjuk értő háttértudással. Idézet Stephen Skinner: Szakrális geometria című könyvének 48. oldaláról: ,,A logaritmikus vagy szögazonos spirál keletkezésének kulcsszáma a phi (az aranymetszési állandó). A logaritmikus spirál olyan örvénylő négyszögekből áll, amelyek ‐ a középponttól kifelé haladva ‐ a phi által irányított harmonikus rendben növekednek $\text{...}$ kezdőpontja van, vége azonban nincs $\text{...}$'' De mi ‐ tudjuk, hogy a $\Phi =\frac{1+\sqrt[]{5}}{2}$ aranymetszési állandó bármely más $q>1$ valós számmal helyettesíthető; ‐ tudjuk, hogy nem lehet kezdőpontja, mert az $e^{k\phi }$ értéke egyetlen $\phi$ esetén sem 0. Hasonló mondatokat találunk a Vince Kiadó által 2009-ben megjelentetett A titkos kód című könyvben (127. oldal): ‐ ,,$\text{...}$ Ebben a spirálban benne foglaltatik a $\Phi$ harmóniájának és egyensúlyának gyönyörűséges titka.'' A mellékelt szerkesztési utasítás lényegében megegyezik a cikk 4. ábrájának rajzaival. De mi ‐ tudjuk, hogy az így kapott görbe valóban csodás matematikai közelítés, de nem maga a logaritmikus spirál; ‐ tudjuk, hogy miért kapta a ,,logaritmikus'' jelzőt; és ‐ tudjuk, hogy a logaritmikus spirál szépségei, önmagát sokszorozó végtelensége a $\Phi$ különleges aránytól függetlenül is elénk tárul.   ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-weight: bold;">Halász Ágnes</span><br> Eötvös József Gimnázium (Budapest)}}\hfill \end{array}}$