Cím:	Megoldásvázlatok a 2011/1. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Gerőcs László
Füzet:	2011/február, 72 - 79. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldásvázlatok a 2011/1. sz. emelt szintű gyakorló feladataihoz   Gerőcs László Budapest   I. rész   1. Egy vásáros vattacukrot és főtt kukoricát árult a piacon. Egy vattacukron $40\%$, egy főtt kukoricán pedig $25\%$ a haszna. Egy napon kétszer annyi vattacukrot adott el, mint főtt kukoricát, és így $36\%$-os lett a haszna. Másnap viszont kétszer annyi főtt kukoricát adott el, mint vattacukrot. Hány százalék haszna lett ezen a napon?  (11 pont)   Megoldás. Legyen $c$ egy vattacukor, $k$ egy kukorica beszerzési és előállítási költsége. Ha az első napon $x$ db kukoricát adott el az árus, akkor a feltételek szerint: $\begin{array}{c}{\displaystyle 1\mathrm{,}4\cdot 2cx+1\mathrm{,}25\cdot kx=\left(kx+2cx\right)\cdot 1\mathrm{,}36.}\end{array}$ Innen egyszerűsítés és rendezés után kapjuk: $\begin{array}{c}{\displaystyle c=\frac{11}{8}k\mathrm{.}}\end{array}$ Ha másnap $y$ db vattacukrot adott el, és e napon a beszerzési és előállítási költség $z$-szerese lett a bevétele, akkor: $\begin{array}{c}{\displaystyle 1\mathrm{,}4\cdot cy+1\mathrm{,}25\cdot 2ky=\left(cy+2ky\right)\cdot z\mathrm{.}}\end{array}$ Ismét egyszerűsítés és összevonás után, felhasználva az előbb $c$ és $k$ között kapott összefüggést: $\begin{array}{c}{\displaystyle z=\frac{1\mathrm{,}4cy+2\mathrm{,}5ky}{cy+2ky}=\frac{1\mathrm{,}4\cdot \frac{11}{8}k+2\mathrm{,}5k}{\frac{11}{8}k+2k}=\frac{1\mathrm{,}4\cdot 11+2\mathrm{,}5\cdot 8}{11+2\cdot 8}\approx 1\mathrm{,}31.}\end{array}$ Tehát a vásáros haszna másnap kb. 31% lett.   2. A BKV megfigyelései alapján az utasoknak kb. $8\%$-a bliccel, azaz érvényes jegy vagy bérlet nélkül utazik a járatokon. $a)$ Mekkora annak a valószínűsége, hogy egy buszon, amelyen $24$-en utaznak, a jegyellenőr nem talál bliccelőt? $b)$ Hány utas esetén lesz legalább $90\%$ annak az esélye, hogy az ellenőr talál bliccelőt a járaton? $c)$ Egy buszon $24$ utas tartózkodott. Mekkora annak a valószínűsége, hogy pontosan két bliccelőt talál az ellenőr?  (12 pont)   Megoldás. $a)$ Annak a valószínűsége, hogy egy véletlenszerűen kiválasztott utas bliccel 0,08, így annak a valószínűsége, hogy az utasnak van érvényes menetjegye vagy bérlete 0,92%. Ezek szerint annak a valószínűsége, hogy a 24 utas mindegyikének van érvényes menetjegye vagy bérlete $\begin{array}{c}{\displaystyle 0\mathrm{,}{92}^{24}\approx 0\mathrm{,}135.}\end{array}$ (Ez meglehetősen kicsi valószínűség, így 24 utas közül már elég nagy eséllyel (86,5%) talál bliccelőt az ellenőr.) $b)$ Ha annak az esélye, hogy talál bliccelőt az ellenőr legalább 90%, akkor annak az esélye, hogy nem talál bliccelőt kisebb, mint 10%, azaz annak a valószínűsége, hogy nem talál bliccelőt kisebb, mint 0,1. Mivel annak a valószínűsége, hogy $n$ utas között nincs bliccelő $0\mathrm{,}{92}^n$, így a $0\mathrm{,}{92}^n<0\mathrm{,}1$ egyenlőtlenséget kell megoldanunk. Vegyük mindkét oldal 10-es alapú logaritmusát: $\begin{array}{c}{\displaystyle \text{lg}0\mathrm{,}{92}^n<\text{lg}0\mathrm{,}\mathrm{1,}\text{azaz}n\cdot \text{lg}0\mathrm{,}92<\text{lg}0\mathrm{,}1.}\end{array}$ Most elosztjuk az egyenlőtlenség mindkét oldalát $\text{lg}0\mathrm{,}92$-dal, de vigyázzunk, mert $\text{lg}0\mathrm{,}92$ negatív szám, így az egyenlőtlenség iránya megfordul: $\begin{array}{c}{\displaystyle n>\frac{\text{lg}0\mathrm{,}1}{\text{lg}0\mathrm{,}92}\approx \frac{-1}{-0\mathrm{,}0362}\approx 27\mathrm{,}6.}\end{array}$ Tehát 28 utas esetén már legalább 90%-os annak az esélye, hogy találunk bliccelőt a járaton. $c)$ Annak a valószínűsége, hogy egy véletlenszerűen ellenőrzött utas bliccel 0,08, annak a valószínűsége, hogy nem bliccel, 0,92. A 24 utas közül a két bliccelőt $\left(\genfrac{}{}{0ex}{}{24}{2}\right)$-féleképpen választhatjuk ki. Így ‐ a binomiális eloszlás szerint ‐ annak a valószínűsége, hogy a 24 utas között pontosan két bliccelő van: $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{24}{2}\right)\cdot 0\mathrm{,}{08}^2\cdot 0\mathrm{,}{92}^{22}\approx 0\mathrm{,}282.}\end{array}$ Tehát kb. 28,2% az esélye annak, hogy 24 utas között pontosan két bliccelőt találunk.   3. 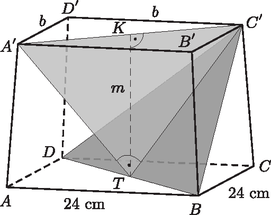Az $ABCDA\text{'}B\text{'}C\text{'}D\text{'}$ négyzet alapú egyenes csonkagúla egyik határoló négyzetének oldala 24 cm (lásd az ábrát). Tudjuk, hogy a $BC\text{'}D$ háromszög szabályos, az $A\text{'}TC\text{'}$ háromszög pedig derékszögű, ahol $T$ a 24 cm oldalú négyzet átlóinak a metszéspontja. Mekkora a gúla térfogata?  (14 pont)     Megoldás. A csonkagúla másik határoló négyzetének oldalát, valamint a testmagasságot kell kiszámítanunk (ábránkon ezeket $b$-vel, illetve $m$-mel jelöltük). A $BDC\text{'}$ szabályos háromszög oldalai az $ABCD$ négyzet átlójával egyenlők: $BD=DC\text{'}=BC\text{'}=24\sqrt[]{2}$. E háromszög $C\text{'}T$ magassága: $\begin{array}{c}{\displaystyle C\text{'}T=\frac{24\sqrt[]{2}\cdot \sqrt[]{3}}{2}=12\sqrt[]{6}\mathrm{.}}\end{array}$ $C\text{'}T$ az $A\text{'}TC\text{'}$ egyenlő szárú derékszögű háromszög befogóival is egyenlő. Ezek szerint az $A\text{'}TC\text{'}$ háromszög $A\text{'}C\text{'}$ átfogója: $\begin{array}{c}{\displaystyle A\text{'}C\text{'}=12\sqrt[]{6}\sqrt[]{2}=12\sqrt[]{12}=24\sqrt[]{3}\mathrm{.}}\end{array}$ Ebből pedig az $A\text{'}B\text{'}C\text{'}D\text{'}$ négyzet $b$ oldala: $\begin{array}{c}{\displaystyle b=\frac{24\sqrt[]{3}}{\sqrt[]{2}}=12\sqrt[]{6}\mathrm{.}}\end{array}$ A csonkagúla $m$ magassága az $A\text{'}TC\text{'}$ egyenlő szárú derékszögű háromszög átfogóhoz tartozó magassága, tehát: $\begin{array}{c}{\displaystyle m=KT=\frac{A\text{'}C\text{'}}{2}=12\sqrt[]{3}\mathrm{.}}\end{array}$ Most már minden megvan ahhoz, hogy meghatározzuk a csonkagúla $V$ térfogatát: $\begin{array}{c}{\displaystyle V=\frac{12\sqrt[]{3}}{3}\cdot \left({24}^2+24\cdot 12\sqrt[]{6}+{\left(12\sqrt[]{6}\right)}^2\right)=4\sqrt[]{3}\cdot \left(576+288\sqrt[]{6}+864\right)\approx 14864\mathrm{,}1.}\end{array}$ Vagyis a térfogat kb. 14 864,1 cm${}^3$.   Megjegyzés. A feladat szövegében az egyik határoló négyzet oldalhossza volt adott. Érdemes észrevenni, hogy a csonkagúla ,,fedőnégyzetének'' $b$ oldala ennél nagyobb lett.   4. Pisti külföldi útja során meglátott egy kirakatban egy igen kedvező árú laptopot, melynek ára euróban háromjegyű pozitív egész szám volt. Bement, hogy megvásárolja, de döbbenten tapasztalta, hogy a pénztárnál $1$ euróval kevesebbet számláztak, mint a kirakatban látott ár kétszerese. Mikor reklamált, kiderült, hogy a kirakatban az árcédulán a számjegyeket véletlenül fordított sorrendben írták ki. Mennyibe került a laptop?  (14 pont)   Megoldás. Ha a kirakatban látott ár $\overline{cba}$, azaz a valódi ár $\overline{abc}$. A pénztárnál $2\cdot \overline{cba}-1$ eurót kértek Pistitől. A feltételek szerint: $\begin{array}{c}{\displaystyle \overline{abc}+1=2\cdot \overline{cba}\mathrm{.}}\end{array}$ Az egyenlet jobb oldala páros, így a bal oldalnak is párosnak, tehát $c$-nek páratlannak kell lennie. De $c<5$ kell, hogy legyen, ugyanis ellenkező esetben az egyenlet jobb oldalán már négyjegyű szám szerepelne, de a bal oldal csak háromjegyű (az $\overline{abc}=999$ eset nyilván kizárható). Ezek szerint $c=1$ vagy $c=3$. Ha $c=1$, akkor az egyenlet bal oldala 2-re végződik. Ekkor a jobb oldalon $a=1$ vagy $a=6$ lehet. De $a=1$ esetén a bal oldal 200-nál kisebb, míg a jobb oldal 200-nál nagyobb lenne, tehát $a=1$ nem lehetséges. Ha $a=6$, akkor a bal oldal 600-nál nagyobb, míg a jobb pedig 400-nál kisebb lenne, így ez is lehetetlen. Ha $c=3$, akkor a bal oldali szám 4-re végződik, így a jobb oldalon $a=2$, vagy $a=7$. Ha $a=2$, akkor a bal oldal 300-nál kisebb, míg a jobb oldal 600-nál nagyobb lenne, ami lehetetlen. Végül, ha $a=7$, akkor az egyenlet így alakul: $\begin{array}{c}{\displaystyle \overline{7b3}+1=2\cdot \overline{3b7}\mathrm{,}\text{azaz}704+10b=614+20b\mathrm{,}\text{ahonnan}b=9.}\end{array}$ Tehát Pisti a kirakatban a 397-et látta, a valóságos ár pedig 793 euró.   II. rész   5. $a)$ A valós számok halmazán értelmezett $f\left(x\right)=a{x}^2+bx+c$ függvényről tudjuk, hogy egyetlen zérushelye az $x=1$-ben van és $f\left(2\right)=2$. Határozzuk meg az $a$, $b$, $c$ együtthatókat. $b)$ Legyenek a valós számok halmazán értelmezett függvények $g\left(x\right)=x^2-3x+2$ és $h\left(x\right)=2x-a$. Határozzuk meg az $a$ valós paraméter értékét úgy, hogy a $g\left(h\left(x\right)\right)=h\left(g\left(x\right)\right)$ egyenletnek ne legyen valós megoldása.  (16 pont)   Megoldás. $a)$ A feltételek alapján az alábbi egyenletrendszert írhatjuk fel: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle b^2-4ac}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle a+b+c}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle 4a+2b+c}& {\displaystyle =2.}\hfill \end{array}}\}\mathrm{.}}\end{array}$ A második egyenletből: $c=-a-b$. Ezt az első és a harmadik egyenletbe helyettesítve kapjuk: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle b^2+4a^2+4ab}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle 3a+b}& {\displaystyle =2.}\hfill \end{array}}\}\mathrm{.}}\end{array}$ A második egyenletből: $b=2-3a$. Ezt az első egyenletbe helyettesítve kapjuk: $\begin{array}{c}{\displaystyle {\left(2-3a\right)}^2+4a^2+4a\left(2-3a\right)=\mathrm{0,}\text{ahonnan}{a}^2-4a+4={\left(a-2\right)}^2=\mathrm{0,}}\end{array}$ tehát $a=2$. Ezt visszahelyettesítve: $b=-4$, $c=2$. A keresett együtthatók: $a=2$, $b=-4$, $c=2$. $b)$ Ha $g\left(x\right)=x^2-3x+2$ és $h\left(x\right)=2x-a$, akkor $\begin{array}{c}{\displaystyle g\left(h\left(x\right)\right)={\left(2x-a\right)}^2-3\left(2x-a\right)+2\text{és}h\left(g\left(x\right)\right)=2\left(x^2-3x+2\right)-a\mathrm{.}}\end{array}$ Tehát $4x^2-4ax+a^2-6x+3a+2=2x^2-6x+4-a$, azaz $2x^2-4ax+a^2+4a-2=0$. Ennek az egyenletnek akkor és csak akkor nincs valós gyöke, ha diszkriminánsa negatív: $\begin{array}{c}{\displaystyle 16a^2-8\left(a^2+4a-2\right)<\mathrm{0,}\text{ahonnan}{a}^2-4a+2<0.}\end{array}$ A másodfokú kifejezés zérushelyei: $a_{\mathrm{1,2}}=2\pm \sqrt[]{2}$, így az egyenlőtlenség megoldása: $2-\sqrt[]{2}<a<2+\sqrt[]{2}$. Ezek lesznek a feladatban keresett $a$ valós paraméterek.   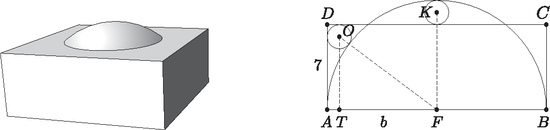6. Egy arab épületet és annak egy tengelymetszetét látjuk az ábrán. A tengelymetszet $ABCD$ téglalapjának $AD$ oldala 7 m, $AB$ oldala pedig nagyobb, mint 14 m. Egy kis kör érinti az $AD$ és $DC$ oldalakat, valamint kívülről érinti az $AB$ oldalra emelt félkört. Egy másik kis kör a $DC$ oldalt és a félkört belülről érintő körök legnagyobbika. Mekkora e kis körök sugara, ha tudjuk, hogy e sugarak egyenlők?  (16 pont)     Megoldás. Legyen $b$ a téglalap hosszabbik oldala, és legyenek $K$ és $O$ a keresett $x$ sugarú körök középpontjai. Az ábra alapján: $\begin{array}{c}{\displaystyle KF=7+x=\frac{b}{2}-x\mathrm{.}}\end{array}$ Az $OTF$ derékszögű háromszögben a Pitagorasz-tétel alapján: $\begin{array}{c}{\displaystyle {\left(\frac{b}{2}+x\right)}^2={\left(\frac{b}{2}-x\right)}^2+{\left(7-x\right)}^2\mathrm{.}}\end{array}$ Az előző egyenletet is felhasználva azt kapjuk, hogy $\begin{array}{c}{\displaystyle {\left(7+3x\right)}^2={\left(7+x\right)}^2+{\left(7-x\right)}^2\mathrm{,}\text{ahonnan}7x^2+42x-49=0.}\end{array}$ Az egyenlet egyetlen pozitív gyöke $x=1$, tehát a kis körök sugara 1 m.   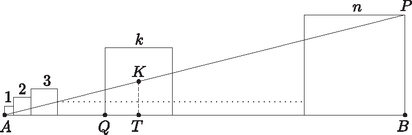7. Egymás mellé rajzoltunk $n$ db négyzetet. Az egyes négyzetek oldalai sorban $\mathrm{1,2,3,}\text{...}\mathrm{,}n$ (lásd az ábrát). Van-e olyan négyzet, melynek területét az $AP$ szakasz felezi?  (16 pont)     Megoldás. Ha egy egyenes felezi egy négyzet területét, akkor át kell haladnia a négyzet középpontján. Ha az $AP$ egyenes a $k$-adik négyzet területét felezi, akkor a $KTA$ és $PBA$ nyilvánvalóan hasonló háromszögekre: $\begin{array}{c}{\displaystyle \frac{AT}{TK}=\frac{AB}{BP}\mathrm{.}}\end{array}$ Az egyenlőségben szereplő egyes szakaszok: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle AT}& {\displaystyle =1+2+3+\text{...}+\left(k-1\right)+\frac{k}{2}=\frac{k\left(k-1\right)}{2}+\frac{k}{2}=\frac{k^2}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle TK}& {\displaystyle =\frac{k}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle AB}& {\displaystyle =1+2+3+\text{...}+n=\frac{n\left(n+1\right)}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle BP}& {\displaystyle =n\mathrm{.}}\hfill \end{array}}$ Ezek szerint: $\begin{array}{c}{\displaystyle \frac{\frac{k^2}{2}}{\frac{k}{2}}=\frac{\frac{n\left(n+1\right)}{2}}{n}\mathrm{,}\text{azaz}k=\frac{n+1}{2}\mathrm{.}}\end{array}$ Ez akkor lesz egész szám, ha $n$ páratlan. Tehát csak akkor lesz olyan négyzet, melynek a területét az $AP$ szakasz felezi, ha a négyzetek száma páratlan, és ekkor a $k=\frac{n+1}{2}$-edik négyzet területét felezi a kérdéses egyenes.   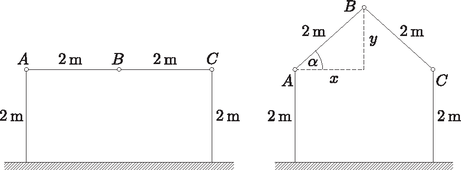8. Egy összecsukható sátor vázát látjuk az ábrán. A két 2 m magas függőleges rúd között az $A$, $B$ és $C$ pontokban található csuklók mentén állítható a sátor keresztmetszetének váza oly módon, hogy a két függőleges rudat közelítjük egymáshoz. A rudak 2 m hosszúak. A sátor használói tapasztalatból tudják, hogy a két függőleges rudat egymáshoz közelítve, a sátor légtere egy darabig növekszik, aztán újra csökken. $a)$ Számítsuk ki $\alpha ={20}^{\circ }$ esetén a sátor keresztmetszetének területét. $b)$ Mekkora $\alpha$ szög esetén lesz a sátor légtere maximális?  (16 pont)     Megoldás. $a)$ A ferde tetőknek a vízszintessel bezárt szöge legyen $\alpha$. A keresztmetszet területe ekkor egy téglalap és egy egyenlő szárú háromszög területének összegével egyenlő. A téglalap egyik oldala 2, a másik oldala $2x$, ahol $x=2\text{cos}\alpha$. Tehát a téglalap területe: $\begin{array}{c}{\displaystyle T_{\text{téglalap}}=2\cdot 2x=4\cdot 2\text{cos}\alpha =8\text{cos}\alpha \mathrm{.}}\end{array}$ Az $ABC$ egyenlő szárú háromszög alapja és $y$ magassága: $\begin{array}{c}{\displaystyle AC=2x=4\text{cos}\alpha \mathrm{,}y=2\text{sin}\alpha \mathrm{.}}\end{array}$ Így az $ABC$ háromszög területe: $\begin{array}{c}{\displaystyle T_{ABC}=\frac{2xy}{2}=xy=2\text{cos}\alpha \cdot 2\text{sin}\alpha =4\text{cos}\alpha \cdot \text{sin}\alpha \mathrm{.}}\end{array}$ Ezek szerint a keresztmetszet területe $\alpha$ függvényében: $\begin{array}{c}{\displaystyle T\left(\alpha \right)=8\text{cos}\alpha +4\text{cos}\alpha \text{sin}\alpha \mathrm{,}\text{ahol}0\le \alpha \le {90}^{\circ }\mathrm{.}}\end{array}$ Vagyis $T\left({20}^{\circ }\right)\approx 8\mathrm{,}803\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}$. $b)$ A tapasztalatok alapján tudjuk, hogy a keresztmetszet területének egy bizonyos $\alpha$-nál maximuma van, vagyis tudjuk, hogy valamely $\alpha$ esetén a $T\left(\alpha \right)$ függvény deriváltja 0-val egyenlő. Ezt az $\alpha$ értéket kell meghatároznunk. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T\text{'}\left(\alpha \right)}& {\displaystyle =8\left(-\text{sin}\alpha \right)+4\left(\text{cos}\alpha \text{sin}\alpha \right)\text{'}=8\left(-\text{sin}\alpha \right)+4\left(-\text{sin}{}^2\alpha +\text{cos}{}^2\alpha \right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =-8\text{sin}\alpha +4\left(-\text{sin}{}^2\alpha +1-\text{sin}{}^2\alpha \right)=-8\text{sin}{}^2\alpha -8\text{sin}\alpha +4=\mathrm{0,}}\hfill \end{array}}$ azaz: $\begin{array}{c}{\displaystyle 2\text{sin}{}^2\alpha +2\text{sin}\alpha -1=0.}\end{array}$ A $\text{sin}\alpha$-ra kapott másodfokú egyenlet megoldása: $\begin{array}{c}{\displaystyle {\left(\text{sin}\alpha \right)}_{\mathrm{1,2}}=\frac{-2\pm \sqrt[]{4+8}}{4}=\frac{-2\pm 2\sqrt[]{3}}{4}=\frac{-1\pm \sqrt[]{3}}{2}\mathrm{.}}\end{array}$ A negatív gyök nyilván nem jöhet számításba, hiszen $\alpha$ hegyesszög, így: $\begin{array}{c}{\displaystyle \text{sin}\alpha =\frac{\sqrt[]{3}-1}{2}\approx 0\mathrm{,}\mathrm{366,}\text{ahonnan}\alpha \approx 21\mathrm{,}{47}^{\circ }\mathrm{.}}\end{array}$ Vagyis kb. 21,47${}^{\circ }$ esetén lesz a sátor légtere a lehető legnagyobb.   9. Legyenek $a$ és $b$ $1$-nél nagyobb valós számok. Egy téglatest élei $\text{log}{}_{a}b$, $\text{log}{}_{b}a$ és $\text{log}{}_{a}ab$. Bizonyítsuk be, hogy a téglatest felszínének mérőszáma a térfogat mérőszámának több mint $4$-szerese.  (16 pont)   Megoldás. A téglatest térfogata: $V=\text{log}{}_{a}b\cdot \text{log}{}_{b}a\cdot \text{log}{}_{a}ab$. Mivel $\text{log}{}_{a}b\cdot \text{log}{}_{b}a=1$, így $V=\text{log}{}_{a}ab=1+\text{log}{}_{a}b$. A téglatest felszíne: $\begin{array}{c}{\displaystyle A=2\cdot \left[\text{log}{}_{a}b\cdot \text{log}{}_{b}a+\text{log}{}_{a}b\cdot \text{log}{}_{a}ab+\text{log}{}_{b}a\cdot \text{log}{}_{a}ab\right]\mathrm{.}}\end{array}$ Ez tovább alakítva: $\begin{array}{c}{\displaystyle A=2\cdot \left[1+\text{log}{}_{a}ab\left(\text{log}{}_{a}b+\text{log}{}_{b}a\right)\right]=2\cdot \left[1+V\cdot \left(\text{log}{}_{a}b+\text{log}{}_{b}a\right)\right]\mathrm{.}}\end{array}$ Osszuk el a kapott egyenlet mindkét oldalát $V$-vel: $\begin{array}{c}{\displaystyle \frac{A}{V}=2\cdot \left[\frac{1}{V}+\text{log}{}_{a}b+\text{log}{}_{b}a\right]\mathrm{.}}\end{array}$ A zárójelen belül a második és a harmadik tag egy pozitív számnak és reciprokának összege. Erről ismert, hogy értéke legalább 2. Ehhez a pozitív $\frac{1}{V}$-t hozzáadva nyilván: $\begin{array}{c}{\displaystyle \frac{1}{V}+\text{log}{}_{a}b+\text{log}{}_{b}a>\mathrm{2,}\text{így}\frac{A}{V}>\mathrm{4,}\text{azaz}A>4V\mathrm{.}}\end{array}$ Tehát a felszín mérőszáma valóban nagyobb a térfogat mérőszámának négyszeresénél.