Cím:	A 2010. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása
Szerző(k):	Fleiner Tamás
Füzet:	2011/február, 67 - 70. oldal	PDF  |  MathML
Témakör(ök):	Matematika, Kürschák József (korábban Eötvös Loránd), Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A 2010. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldása   Fleiner Tamás   1. feladat. Adott $n$ lezárt bőrönd és $n$ kulcs úgy, hogy a bőröndök mindegyikét pontosan egy kulcs nyitja és mindegyik kulcs pontosan egy bőröndöt nyit. Célunk az, hogy az összes bőröndről megállapítsuk, melyik kulcs nyitja. Egy próbálkozás abból áll, hogy valamelyik kulccsal megpróbálunk kinyitni egy bőröndöt. Határozzuk meg azt a legkisebb $p\left(n\right)$ számot, amelyhez létezik olyan eljárás, hogy azt végrehajtva legfeljebb $p\left(n\right)$ próbálkozás után bizonyosan ismerni fogjuk az $n$ összetartozó bőrönd‐kulcs párt.   Megoldás. Megmutatjuk, hogy $n\ge 1$ esetén $p\left(n\right)=\left(\genfrac{}{}{0ex}{}{n}{2}\right)$. Az alábbi eljárás legfeljebb $\left(\genfrac{}{}{0ex}{}{n}{2}\right)$ próbálkozásból oldja meg a feladatot, azaz $p\left(n\right)\le \left(\genfrac{}{}{0ex}{}{n}{2}\right)$. Legyenek a kulcsok $k_1\mathrm{,}{k}_2\mathrm{,}\text{...}\mathrm{,}{k}_n$, és jelölje $b_i$ azt a bőröndöt, amit $k_i$ nyit. Célunk a $b_i$ megtalálása minden $i$-re. A $k_1$ kulcsot próbáljuk bele az első néhány bőröndbe, amíg ki nem derül, melyik a $b_1$. Ehhez legfeljebb $n-1$ próbálkozás kell, mert amint már $\left(n-1\right)$-szer sikertelenül próbálkoztunk, azonnal tudjuk, hogy $k_1$ bizonyosan az utolsó, ki nem próbált bőröndöt nyitja. A $k_2$ kulccsal is tegyük ugyanezt, azzal a megszorítással, hogy a $b_1$ bőrönddel semmiképp se próbálkozzunk. Hasonló okból legfeljebb $n-2$ próbálkozást végzünk addig, amíg meg nem találjuk $b_2$-t. Általában, a $b_1\mathrm{,}{b}_2\mathrm{,}\text{...}\mathrm{,}{b}_{i-1}$ bőröndök megtalálása után a $b_i$-t keressük meg úgy, hogy a $k_i$ kulcsot sorra belepróbáljuk a lehetséges $n-\left(i-1\right)=n-i+1$ bőröndbe. Világos, hogy legfeljebb $n-i$ próbálkozás után megtaláljuk $b_i$-t. Összességében tehát nem több, mint ${\sum }_{i=1}^n\left(n-i\right)=\left(\genfrac{}{}{0ex}{}{n}{2}\right)$ próbálkozást végzünk. Megmutatjuk másrészt, hogy $p\left(n\right)\ge \left(\genfrac{}{}{0ex}{}{n}{2}\right)$, azaz $\left(\genfrac{}{}{0ex}{}{n}{2}\right)$-nél kevesebb próbálkozást megengedve nem lehetünk bizonyosak afelől, hogy mindig megtaláljuk az összetartozó bőrönd-kulcs párokat. Tegyük fel, hogy egy olyan módszer szerint próbáljuk a kulcsokat a bőröndökhöz, amely beazonosítja az összetartozó bőrönd-kulcs párokat, másrészt az ehhez felhasznált próbálkozásszámok lehetséges legnagyobbika is a lehető legkisebb. Világos, hogy ezen stratégia szerint eljárva sosem fogunk belepróbálni egy kulcsot egy bőröndbe akkor, ha már a próba előtt bizonyosak lehetünk afelől, hogy az adott kulcs nyitja a szóban forgó bőröndöt. Ez azt jelenti, hogy fel kell arra készülnünk, hogy csupa sikertelen próbálkozás alapján kell megbizonyosodnunk az összes összetartozó $\left(b_i\mathrm{,}{k}_i\right)$ bőrönd-kulcs párról. Ha ez megtörtént, és valamely $1\le i<j\le n$ esetén nem próbáltuk bele sem a $k_i$ kulcsot a $b_j$ bőröndbe, sem a $k_j$ kulcsot a $b_i$ bőröndbe, akkor az elvégzett próbálkozásaink alapján nem zárhatjuk ki azt a lehetőséget, hogy a $k_i$ kulcs a $b_j$ bőröndöt, a $k_j$ kulcs pedig a $b_i$ bőröndöt nyitja, míg a többi kulcs ahhoz a bőröndhöz tartozik, amelyikhez eddig gondoltuk. Ez pedig azt jelentené, hogy mégsem tudjuk bizonyosan összepárosítani a kulcsokat és bőröndöket. Tehát tetszőleges $1\le i<j\le n$ esetén a $k_i-b_j$ és a $k_j-b_i$ próbák valamelyikét el kell végeznünk. Mivel különböző $\left(i\mathrm{,}j\right)$ párokhoz ezen próbák különböznek, legalább annyi próbálkozásra van szükség, ahányféleképpen különböző $i$-t és $j$-t tudunk választani, vagyis legalább $\left(\genfrac{}{}{0ex}{}{n}{2}\right)$-re. Ezzel megmutattuk, hogy $p\left(n\right)\ge \left(\genfrac{}{}{0ex}{}{n}{2}\right)$, és ezt összevetve a korábban igazolt $p\left(n\right)\le \left(\genfrac{}{}{0ex}{}{n}{2}\right)$ egyenlőtlenséggel éppen a bizonyítani kívánt $p\left(n\right)=\left(\genfrac{}{}{0ex}{}{n}{2}\right)$ állítás adódik.  $\square$   Megjegyzések. 1. A fenti bizonyítás kulcslépése az alsó becslés bizonyítása, azon belül is az ,,ellenség módszer'' alkalmazása, amikor is azt indokoljuk, hogy csupa negatív próba után is össze kell tudnunk párosítani a kulcsokat a bőröndökkel. 2. Ez az alsó becslés gráfelméleti nyelven is elmondható. Tekintsük azt a $G$ gráfot, amelynek csúcsai a bőröndök és a kulcsok, él pedig az összetartozó párok között fut. Világos, hogy minden egyes próbálkozás egy-egy lehetséges bőrönd-kulcs él $G$-beliségének ,,lekérdezését'' jelenti, célunk pedig a $G$ gráf meghatározása. Az ellenség-módszert (adversary method) használó érv azt indokolja, hogy akkor is meg kell tudnunk határozni $G$-t, ha minden értelmes lekérdezéskor az derül ki, hogy az adott él nincs $G$-ben. A fent közölt bizonyítás úgy is elmondható, hogy ha $G$-t sikerült így meghatároznunk, akkor tetszőleges $i\ne j$-re le kellett kérdeznünk a $k_i{b}_j$ és $k_j{b}_i$ élek közül legalább az egyiket. Máshogyan is igazolhatjuk az alsó becslést. Ha a lekérdezések negatív eredményei egyértelműen meghatározzák $G$-t, akkor a le nem kérdezett $k-b$ élek nem alkothatnak alternáló kört a $G$ gráf éleivel. Ekkor ugyanis nem lenne az kizárható, hogy e körnek a $G$-n kívüli élei mentén tartoznak össze a kulcsok és bőröndök. (A fenti bizonyításban $4$ hosszú alternáló körrel dolgoztunk.) Innen könnyen igazolható, hogy valamelyik bőrönd vagy kulcs legalább $n-1$ próbálkozásban szerepelt. Feltehető, hogy ez a $k_n$ vagy $b_n$ valamelyike. Ugyanilyen megfontolással látható, hogy a $b_1\mathrm{,}{b}_2\mathrm{,}\text{...}{b}_{n-1}$ bőröndök, illetve a $k_1\mathrm{,}{k}_2\mathrm{,}\text{...}\mathrm{,}{k}_{n-1}$ kulcsok valamelyike (mondjuk az $n-1$ indexű) legalább $n-2$ olyan próbálkozásban szerepelt, amelyben nem szerepelt sem $b_n$, sem $k_n$. A gondolatmenetet folytatva meg lehet mutatni, hogy az összetartozó $b_i{k}_i$ bőrönd‐kulcs párokat el tudjuk látni indexszel úgy, hogy minden $1\le i\le n$ esetén a $b_i$ vagy a $k_i$ legalább $i-1$ olyan próbálkozásban vett részt, amelyben $b_{i+1}\mathrm{,}\text{...}\mathrm{,}{b}_n$ és $k_{i+1}\mathrm{,}\text{...}\mathrm{,}{k}_n$ egyikét sem használtuk. 3. Többen próbálkoztak a fentihez hasonló érveléssel. Volt, aki elkövette azt a hibát, hogy a le nem kérdezett élek gráfjának körmentességét próbálta igazolni. Sajnos ez általában nem igaz. Valójában ez a gráf a $G$ éleivel alternáló kört nem tartalmazhat. Szerencsére, ahogy azt az előző megjegyzésbeli bizonyítás vázlat mutatja, már ez is elég az alsó becsléshez. 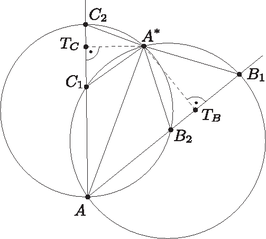  2. feladat. Az $ABC$ háromszög $AB$ oldalának belsejében adottak a $C_1$ és $C_2$ pontok, a $BC$ oldal belsejében az $A_1$ és $A_2$ pontok, végül a $CA$ oldal belsejében a $B_1$ és $B_2$ pontok úgy, hogy $A{C}_1<A{C}_2$, $B{A}_1<B{A}_2$ és $C{B}_1<C{B}_2$ teljesül. Az $A{B}_1{C}_1$ és $A{B}_2{C}_2$ körök $A$-tól különböző metszéspontját jelölje $A^{*}$, a $B{C}_1{A}_1$ és $B{C}_2{A}_2$ körök $B$-től különböző metszéspontja legyen $B^{*}$, végül a $C{A}_1{B}_1$ és $C{A}_2{B}_2$ körök $C$-től különböző metszéspontját nevezzük $C^{*}$-nak. Mutassuk meg, hogy az $A{A}^{*}$, $B{B}^{*}$ és $C{C}^{*}$ egyenesek egy ponton mennek át.   Megoldás. A jól ismert Ceva-tétel trigonometrikus alakját fogjuk használni, amely szerint az $A{A}^{*}$, $B{B}^{*}$ és $C{C}^{*}$ egyenesek pontosan akkor mennek át egy ponton, ha $\begin{array}{c}{\displaystyle \frac{\text{sin}BA{A}^{*}\sphericalangle }{\text{sin}CA{A}^{*}\sphericalangle }\cdot \frac{\text{sin}AC{C}^{*}\sphericalangle }{\text{sin}BC{C}^{*}\sphericalangle }\cdot \frac{\text{sin}CB{B}^{*}\sphericalangle }{\text{sin}AB{B}^{*}\sphericalangle }=1.}\end{array}$     Az első tört kiszámításához figyeljük meg, hogy $A{B}_2{A}^{*}{C}_2$ húrnégyszög, ezért $A{C}_2{A}^{*}\sphericalangle =A^{*}{B}_2{B}_1\sphericalangle$; továbbá $A{B}_1{A}^{*}\sphericalangle =A^{*}{C}_1{C}_2\sphericalangle$, hiszen $A{B}_1{A}^{*}{C}_1$ is húrnégyszög. A megfelelő szögek egyenlősége miatt tehát $A^{*}{C}_1{C}_2▵\sim A^{*}{B}_1{B}_2▵$, így a megfelelő oldalak aránya megegyezik a hozzájuk tartozó magasságok arányával, vagyis $\begin{array}{c}{\displaystyle \frac{|B_1{B}_2|}{|C_1{C}_2|}=\frac{|A^{*}{T}_B|}{|A_{*}{T}_C|}\mathrm{,}}\end{array}$ ahol rendre $T_B$, illetve $T_C$ jelöli az $A^{*}$-ból az $AB$, illetve $AC$ egyenesekre bocsátott merőlegesek talppontjait. Tudjuk még, hogy $\begin{array}{c}{\displaystyle \text{sin}BA{A}^{*}\sphericalangle =\frac{|A^{*}{T}_B|}{|A{A}^{*}|}\mathrm{,}\text{illetve}\text{sin}CA{A}^{*}\sphericalangle =\frac{|A^{*}{T}_C|}{|A{A}^{*}|}\mathrm{,}}\end{array}$ ezért $\begin{array}{c}{\displaystyle \frac{\text{sin}BA{A}^{*}\sphericalangle }{\text{sin}CA{A}^{*}\sphericalangle }=\frac{|A^{*}{T}_B|}{|A^{*}{T}_C|}=\frac{|B_1{B}_2|}{|C_1{C}_2|}\mathrm{.}}\end{array}$ Hasonlóan látható be, hogy $\begin{array}{c}{\displaystyle \frac{\text{sin}AC{C}^{*}\sphericalangle }{\text{sin}BC{C}^{*}\sphericalangle }=\frac{|A_1{A}_2|}{|B_1{B}_2|}\mathrm{,}\text{illetve}\frac{\text{sin}CB{B}^{*}\sphericalangle }{\text{sin}AB{B}^{*}\sphericalangle }=\frac{|C_1{C}_2|}{|A_1{A}_2|}\mathrm{.}}\end{array}$ A Ceva-tételben szereplő szorzatra tehát $\begin{array}{c}{\displaystyle \frac{\text{sin}BA{A}^{*}\sphericalangle }{\text{sin}CA{A}^{*}\sphericalangle }\cdot \frac{\text{sin}AC{C}^{*}\sphericalangle }{\text{sin}BC{C}^{*}\sphericalangle }\cdot \frac{\text{sin}CB{B}^{*}\sphericalangle }{\text{sin}AB{B}^{*}\sphericalangle }=\frac{|B_1{B}_2|}{|C_1{C}_2|}\cdot \frac{|A_1{A}_2|}{|B_1{B}_2|}\cdot \frac{|C_1{C}_2|}{|A_1{A}_2|}=1}\end{array}$ adódik, és nekünk pontosan ezt kellett bizonyítanunk.  $\square$   3. feladat. Mely $n$ és $k$ pozitív egész számokra léteznek $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_n\mathrm{,}{b}_1\mathrm{,}{b}_2\mathrm{,}\text{...}\mathrm{,}{b}_k$ egész számok úgy, hogy az $a_i{b}_j$ szorzatok $(1\le i\le n$, $1\le j\le k)$ páronként különböző maradékot adnak $nk$-val osztva?   Megoldás. Azt állítjuk, hogy pontosan akkor léteznek a kívánt $a_i$ és $b_j$ számok, ha $n$ és $k$ relatív prímek. Ehhez elsőként igazoljuk, hogy az állítás elégséges. Tegyük fel tehát, hogy $\left(n\mathrm{,}k\right)=1$. Legyen $1\le i\le n$ és $1\le j\le k$ esetén $a_i=ik+1$, illetve $b_j=jn+1$. Az $a_i{b}_j=ijnk+ik+jn+1$ szám $n$-nel osztva $ik+1$, $k$-val osztva pedig $jn+1$ maradékot ad. Az $n$ és $k$ relatív prím volta miatt $1\le i\le n$ esetén az $ik+1$ számok páronként különböző maradékot adnak $n$-nel osztva, $1\le j\le k$ esetén pedig a $jn+1$ számok páronként különböző maradékot adnak $k$-val osztva. Ha ugyanis mondjuk $ik+1$ és $i\text{'}k+1$ ugyanazt a maradékot adják $n$-nel osztva, akkor $n\mid ik+1-\left(i\text{'}k+1\right)=\left(i-i\text{'}\right)k$, ahonnan $n\mid \left(i-i\text{'}\right)$ következik, hiszen $n$-nek és $k$-nak nincs közös prímosztója. Ez utóbbi oszthatóság és $1\le i\mathrm{,}i\text{'}\le n$ miatt $i=i\text{'}$. Azt kaptuk tehát, hogy bárhogyan is veszünk két különböző $a_i{b}_j$ szorzatot, azok $n$-nel vagy $k$-val osztva különböző maradékot adnak. Nem lehetséges tehát, hogy két különböző szorzat $nk$-val osztva azonos maradékot adjon, nekünk pedig éppen erre van szükségünk. A szükségesség bizonyításához azt tesszük fel, hogy az $a_i$ és $b_j$ számok rendelkeznek a feladatban leírt tulajdonsággal. Ez azt is jelenti, hogy valamelyik, mondjuk $a_1{b}_1$ szorzat $nk$-val osztva $0$ maradékot ad, azaz $nk\mid a_1{b}_1$. Legyen $a=\left(a_1\mathrm{,}nk\right)$ és $b=\left(b_1\mathrm{,}nk\right)$. Világos, hogy $nk\mid ab$, ezért $nk\le ab$. Figyeljük meg, hogy a $k$ db $a_1{b}_j$ szorzat mindegyike osztható $a$-val. Márpedig az $nk$ szerinti osztási maradékok között pontosan $\frac{nk}{a}$ olyan van, amely $a$-val osztható. Ez azt jelenti, hogy $k\le \frac{nk}{a}$, azaz $a\le n$. Hasonló gondolatmenet igazolja a $b\le k$ becslést. Ezek szerint $ab\le nk$, amit a korábbi $nk\le ab$ megfigyeléssel összevetve azt kapjuk, hogy $ab=nk$. Ez utóbbi pedig csak úgy lehetséges, ha $a=n$ és $b=k$. Jelölje $d$ az $n$ és $k$ legnagyobb közös osztóját. Ekkor $n$ és $k$ legkisebb közös többszöröse $M=\frac{nk}{d}$. Számoljuk meg, hány olyan osztási maradék van $nk$ szerint, amely $n$-nel vagy $k$-val osztható. Világos, hogy $k$ maradék osztható $n$-nel és $n$ maradék $k$-val, ám azokat a maradékokat, amelyek $n$-nel és $k$-val is oszthatók, kétszer számoltuk meg. Ezek éppen az $M$-mel osztható maradékok, számuk tehát $\frac{nk}{M}=d$. Ezért pontosan $n+k-d$ olyan $nk$ szerinti maradék van, amely $n$-nel vagy $k$-val osztható. Azonban $n\mid a_1$ és $k\mid b_1$ miatt az $a_1{b}_j$, illetve $a_i{b}_1$ szorzatok oszthatók $n$-nel, illetve $k$-val. Az ilyen szorzatok száma pedig $n+k-1$, ezért $n+k-1\le n+k-d$, azaz $1\ge d=\left(n\mathrm{,}k\right)$. Ezek szerint $n$ és $k$ valóban relatív prímek, ezzel pedig a feltétel szükségességét is igazoltuk.  $\square$   Megjegyzés. A szükségességet igazoló gondolatmenet Dankovics Attila megoldásából származik.