Cím:	Megoldásvázlatok a 2010/9 sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Gyanó Éva
Füzet:	2011/január, 6 - 11. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldásvázlatok a 2010/8. sz. emelt szintű gyakorló feladataihoz   Gyanó Éva Budapest   I. rész   1. $a)$ Állítsuk növekvő sorrendbe a következő számokat: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle A}& {\displaystyle ={\left({2011}^{\text{sin}\frac{81\pi }{4}}\right)}^{\text{log}{}_2\text{log}{}_3\text{log}{}_{5}125};}\hfill \\ \hfill {\displaystyle B}& {\displaystyle ={\left(\text{sin}\frac{81\pi }{4}+\text{cos}\frac{81\pi }{4}\right)}^2;}\hfill \\ \hfill {\displaystyle C}& {\displaystyle =\text{log}{}_{13-\sqrt[]{168}}\left(13+\sqrt[]{168}\right)\mathrm{.}}\hfill \end{array}}$ $b)$ Igazoljuk, hogy az alábbi kifejezés értéke egész szám: $\begin{array}{c}{\displaystyle \sqrt[3]{2-27\cdot \sqrt[3]{25}+9\cdot \sqrt[3]{{25}^2}}+\sqrt[3]{25}\mathrm{.}}\end{array}$  (12 pont)   Megoldás. $a)$ ${\displaystyle \begin{array}{cc}\hfill {\displaystyle A}& {\displaystyle ={\left({2011}^{\text{sin}\frac{81\pi }{4}}\right)}^{\text{log}{}_2\text{log}{}_3\text{log}{}_{5}125}={\left({2011}^{\text{sin}\frac{\pi }{4}}\right)}^{\text{log}{}_2\text{log}{}_3\text{log}{}_5{5}^3}={\left({2011}^{\frac{\sqrt[]{2}}{2}}\right)}^{\text{log}{}_2\text{log}{}_{3}3}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={2011}^{\frac{\sqrt[]{2}}{2}\cdot \text{log}{}_{2}1}={2011}^0=1.}\hfill \\ \hfill {\displaystyle B}& {\displaystyle ={\left(\text{sin}\frac{81\pi }{4}+\text{cos}\frac{81\pi }{4}\right)}^2={\left(\text{sin}\frac{\pi }{4}+\text{cos}\frac{\pi }{4}\right)}^2={\left(\frac{\sqrt[]{2}}{2}+\frac{\sqrt[]{2}}{2}\right)}^2={\left(2\cdot \frac{\sqrt[]{2}}{2}\right)}^2=2.}\hfill \\ \hfill {\displaystyle C}& {\displaystyle =\text{log}{}_{13-\sqrt[]{168}}\left(13+\sqrt[]{168}\right)=\text{log}{}_{13-\sqrt[]{168}}\left(\frac{1}{13-\sqrt[]{168}}\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\text{log}{}_{13-\sqrt[]{168}}{\left(13-\sqrt[]{168}\right)}^{-1}=-1.}\hfill \end{array}}$ Vagyis: $C<A<B$. $b)$ A köbgyök alatti kifejezés első tagját kettébontva adódik: $\begin{array}{c}{\displaystyle \sqrt[3]{27-27\cdot \sqrt[3]{25}+9\cdot \sqrt[3]{{25}^2}-25}+\sqrt[3]{25}=\sqrt[3]{{\left(3-\sqrt[3]{25}\right)}^3}+\sqrt[3]{25}=3-\sqrt[3]{25}+\sqrt[3]{25}=3.}\end{array}$   2. Egy hajó a folyón egyenletes sebességgel a vízfolyás irányában haladva egy bizonyos utat $5$ óra alatt, ugyanezt az utat a vízfolyással szemben haladva $5$ óra $24$ perc alatt teszi meg. Mennyi idő alatt teszi meg ezt az utat egy tutaj, amely a víz sebességével halad?  (12 pont)   Megoldás. Legyen a hajó óránkénti sebessége állóvízben $v$, a víz sebessége $v_1$. Ekkor a hajó sebessége a vízfolyás irányában $v+v_1$, a vízfolyással szemben $v-v_1$. Ekkor a megtett út: $5\left(v+v_1\right)=5\mathrm{,}4\left(v-v_1\right)$, ebből $v=26v_1$. Azaz: $5\left(26v_1+v_1\right)=135v_1$. A kérdésben szereplő utat a tutaj $v_1$ sebességgel haladva 135 óra alatt teszi meg.   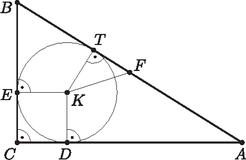3. Egy derékszögű háromszög befogóinak hossza $28$ és $45$. Mennyi a beírható és a köré írható körök középpontjainak távolsága?  (13 pont)   Megoldás. Használjuk az ábra jelöléseit. A két befogó ismeretében a Pitagorasz-tétel segítségével meghatározzuk az átfogó hosszát: $c^2={28}^2+{45}^2=2809$, azaz $c=53$. Mivel a derékszögű háromszög köré írható körének középpontja az átfogó $F$ felezőpontja, így a kör sugara: $R=26\mathrm{,}5$. A beírható kör sugara a külső pontból húzott érintőszakaszok egyenlőségével meghatározható.     Tudjuk, hogy: $BT=BE=a-r$, $AT=AD=b-r$. Ezek alapján: $c=AB=BT+AT=a-r+b-r$, azaz: $\begin{array}{c}{\displaystyle r=\frac{a+b-c}{2}=\frac{28+45-53}{2}=10.}\end{array}$ Mivel $KT=r$ és $BT=BE=a-r=28-10=18$, így $TF=BF-BT=26\mathrm{,}5-18=8\mathrm{,}5$. Alkalmazva a Pitagorasz-tételt a $KTF$ derékszögű háromszögre: $K{F}^2={10}^2+8\mathrm{,}{5}^2=172\mathrm{,}25$, azaz $KF\approx 13\mathrm{,}12$. A keresett távolság kb. 13,12.   4. Az $f\left(x\right)=x^2+ax+b$ $(a\ne 0$; $b\ne 0$; $a\ne b$; $a\in \text{R}$; $b\in \text{R})$ függvényről tudjuk, hogy az $\left(a+b\right)$ helyen felvett helyettesítési értéke $\left(a-4b\right)$, az $\left(a-b\right)$ helyen pedig $\left(a-7b\right)$. Adjuk meg az $f\left(x\right)$ hozzárendelési szabályát.  (14 pont)   Megoldás. $f\left(a+b\right)=a-4b$, azaz $\begin{array}{c}{\displaystyle a-4b={\left(a+b\right)}^2+a\left(a+b\right)+b\mathrm{,}}\end{array}$ (1) $\begin{array}{c}{\displaystyle a-4b=a^2+2ab+b^2+a^2+ab+b\mathrm{.}}\end{array}$ (2) $f\left(a-b\right)=a-7b$, azaz $a-7b={\left(a-b\right)}^2+a\left(a-b\right)+b$. $\begin{array}{c}{\displaystyle a-7b=a^2-2ab+b^2+a^2-ab+b\mathrm{.}}\end{array}$ (3) A (2)-ből elvesszük (3)-at: $3b=6ab$. Mivel $b\ne 0$, azért $a=\frac{1}{2}$. Ezt visszahelyettesítve az (1)-be, kapjuk, hogy $\begin{array}{c}{\displaystyle \frac{1}{2}-4b={\left(\frac{1}{2}+b\right)}^2+\frac{1}{2}\left(\frac{1}{2}+b\right)+b\mathrm{,}}\end{array}$ amiből a $0=b\left(b+\frac{13}{2}\right)$ egyenlet adódik. Mivel $b\ne 0$, azért $b=-\frac{13}{2}$. A keresett függvény hozzárendelési szabálya: $\begin{array}{c}{\displaystyle f\left(x\right)=x^2+\frac{1}{2}x-\frac{13}{2}\mathrm{.}}\end{array}$   II. rész   5. 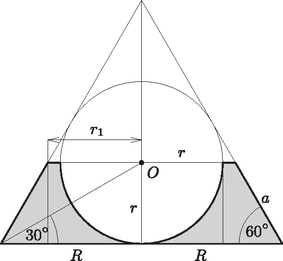Egy $r$ sugarú gömb köré egyenlő oldalú kúpot írunk, a gömb középpontján át a kúp alapjával párhuzamos síkot fektetünk. (Az egyenlő oldalú kúp átmérőjének hossza egyenlő az alkotó hosszával.) Vegyük ki a keletkezett csonkakúpból a benne elhelyezkedő félgömböt. Számítsuk ki az így visszamaradó test felszínét és térfogatát.  (16 pont)   Megoldás. A kérdéses test felszíne az ábrán látható részekből áll.     Az alapkör területe: $\begin{array}{c}{\displaystyle t_1=R^2\pi \mathrm{.}}\end{array}$ A csonkakúp palást felszíne: $\begin{array}{c}{\displaystyle t_2=\left(R+r_1\right)a\pi \mathrm{.}}\end{array}$ A körgyűrű területe: $\begin{array}{c}{\displaystyle t_3=\left(r_1^2-r^2\right)\pi \mathrm{.}}\end{array}$ A félgömb felszíne: $\begin{array}{c}{\displaystyle t_4=2r^2\pi \mathrm{.}}\end{array}$ A területeket az ismert $r$ sugárral kell megadni, ezért $R$, $a$ és $r_1$ értékét kifejezzük $r$ segítségével: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle R}& {\displaystyle =r\cdot \text{ctg}{30}^{\circ }=r\sqrt[]{3}\mathrm{,}}\hfill \\ \hfill {\displaystyle a}& {\displaystyle =\frac{r}{\text{sin}{60}^{\circ }}=r\frac{2}{\sqrt[]{3}}=\frac{2r\sqrt[]{3}}{3}\mathrm{,}}\hfill \\ \hfill {\displaystyle r_1}& {\displaystyle =R-a\text{cos}{60}^{\circ }=r\sqrt[]{3}-\frac{2r\sqrt[]{3}}{3}\cdot \frac{1}{2}=r\sqrt[]{3}\left(1-\frac{1}{3}\right)=\frac{2r\sqrt[]{3}}{3}\mathrm{.}}\hfill \end{array}}$ Ezek alapján: $t_1=3r^2\pi$; $t_2=\frac{10r^2\pi }{3}$; $t_3=\frac{r^2\pi }{3}$; $t_4=2r^2\pi$. Így a felszín: $\begin{array}{c}{\displaystyle A=t_1+t_2+t_3+t_4=\frac{26r^2\pi }{3}\mathrm{.}}\end{array}$ A térfogat a csonkakúp térfogatának és a belőle kivett félgömb térfogatának különbségével egyenlő: $\begin{array}{c}{\displaystyle V=\frac{r\pi }{3}\left(R^2+R{r}_1+r_1^2\right)-\frac{2r^3\pi }{3}\mathrm{.}}\end{array}$ Az $R$ és $r_1$ értékét $r$-rel kifejezve: $V=\frac{13r^3\pi }{9}$.   6. Milyen $\alpha$ értékek mellett lesz az alábbi három kifejezés (ebben a sorrendben) egy számtani sorozat egymást követő eleme: $\text{lg}\text{sin}2\alpha$; $\text{lg}\text{sin}4\alpha$; $\text{lg}\text{cos}2\alpha$?  (16 pont)   Megoldás. A logaritmusok miatt teljesülni kell a következő kikötéseknek:     A három eset együtt: $k\pi <\alpha <\frac{\pi }{4}+k\pi$, $k\in \text{Z}$. A számtani sorozat miatt: $\text{lg}\text{sin}4\alpha -\text{lg}\text{sin}2\alpha =\text{lg}\text{cos}2\alpha -\text{lg}\text{sin}4\alpha$. Alkalmazzuk a logaritmus azonosságait: $\begin{array}{c}{\displaystyle \text{lg}\frac{\text{sin}4\alpha }{\text{sin}2\alpha }=\text{lg}\frac{\text{cos}2\alpha }{\text{sin}4\alpha }\mathrm{,}\text{vagyis:}\frac{2\text{sin}2\alpha \text{cos}2\alpha }{\text{sin}2\alpha }=\frac{\text{cos}2\alpha }{2\text{sin}2\alpha \text{cos}2\alpha }\mathrm{.}}\end{array}$ Elvégezve az egyszerűsítéseket és a megfelelő műveleteket: $\begin{array}{c}{\displaystyle 2\text{sin}2\alpha \text{cos}2\alpha =\frac{1}{2}\mathrm{,}\text{azaz}\text{sin}4\alpha =\frac{1}{2}\mathrm{.}}\end{array}$ A megoldás (figyelembe véve a kikötéseket is): $\begin{array}{c}{\displaystyle {\alpha }_1=\frac{\pi }{24}+k\text{'}\cdot \pi \mathrm{,}k\text{'}\in \text{Z}\mathrm{,}{\alpha }_2=\frac{5\pi }{24}+k\text{'}\text{'}\cdot \pi \mathrm{,}k\text{'}\text{'}\in \text{Z}\mathrm{.}}\end{array}$   7. 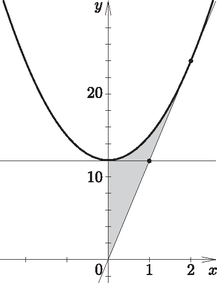Az $f\left(x\right)=3x^2+b$ függvény grafikonjának az $x=2$ helyhez tartozó érintője áthalad az origón. $a)$ Hol metszi ez az érintő a parabola vezéregyenesét? $b)$ Számítsuk ki a függvénygörbe, az érintő, és az $y$ tengely által közbezárt terület nagyságát.  (16 pont)   Megoldás. $a)$ Az érintő áthalad a $P\left(2;f\left(2\right)\right)$ ponton. Mivel $f\left(2\right)=3\cdot 4+b$, így $P\left(2;b+12\right)$. Tudjuk, hogy $f\text{'}\left(x\right)=6x$, ezért az érintő meredeksége: $f\text{'}\left(2\right)=12$. Ezek alapján az érintő egyenlete: $12\left(x-2\right)=y-b-12$, ami $y=12x+b-12$ alakban is írható.     A feltétel szerint ez átmegy az origón, így $b-12=0$, vagyis $b=12$. Így $f\left(x\right)=3x^2+12$, a kérdéses érintő egyenlete pedig: $y=12x$. A parabola paramétere: $p=\frac{1}{6}$, a parabola vezéregyenesének egyenlete: $\begin{array}{c}{\displaystyle y=12-\frac{1}{12}=\frac{143}{12}\mathrm{.}}\end{array}$ Vagyis az érintő a parabola vezéregyenesét a $\left(\frac{143}{144};\frac{143}{12}\right)$ pontban metszi. ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle T}& {\displaystyle ={\int }_0^2\left(3x^2+12\right)dx-{\int }_0^{2}12xdx={\int }_0^2\left(3x^2-12x+12\right)dx=}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle }& {\displaystyle ={\left[3\cdot \frac{x^3}{3}-\frac{12x^2}{2}+12x\right]}_0^2=\left(8-24+24\right)-0=8.}\hfill \end{array}}$   8. A tojásokat 15 db-os dobozokban árulják. Minden tojás $\frac{1}{15}$ valószínűséggel sérült. $a)$ Mekkora a valószínűsége annak, hogy egy doboz csak ép tojásokat tartalmaz? $b)$ Mekkora a valószínűsége annak, hogy egy doboz kettő vagy több törött tojást tartalmaz? $c)$ A boltban tízen vesznek egy-egy doboz tojást. Mekkora a valószínűsége annak, hogy közülük ketten visznek haza csupa ép tojást tartalmazó dobozt?  (16 pont)   Megoldás. $a)$ $P\left(0\text{ db törött}\right)={\left(\frac{14}{15}\right)}^{15}\approx 0\mathrm{,}355$. Vagyis kb. 35,5% a valószínűsége annak, hogy egy doboz csak ép tojásokat tartalmaz. $b)$ Már tudjuk, hogy $P\left(0\text{ db törött}\right)\approx 0\mathrm{,}355$. Kiszámítjuk annak a valószínűségét is, hogy egy doboz pontosan 1 db törött tojást tartalmaz: $\begin{array}{c}{\displaystyle P\left(1\text{ db törött}\right)=15\cdot \frac{1}{15}\cdot {\left(\frac{14}{15}\right)}^{14}\approx 0\mathrm{,}381.}\end{array}$ Ezek alapján: $P\left(\text{kettő vagy több törött}\right)=1-0\mathrm{,}355-0\mathrm{,}381=0\mathrm{,}264$, azaz 26,4%. Vagyis kb. 26,4% a valószínűsége annak, hogy egy doboz kettő vagy több törött tojást tartalmaz. $c)$ Ha nincs a dobozban törött tojás, annak a valószínűsége: 0,355, ha van benne törött, annak a valószínűsége: 0,645. Tehát: $\begin{array}{c}{\displaystyle P=\left(\genfrac{}{}{0ex}{}{10}{2}\right)\cdot 0\mathrm{,}{355}^2\cdot 0\mathrm{,}{645}^8\approx 0\mathrm{,}\mathrm{170,}}\end{array}$ azaz kb. 17%. Vagyis kb. 17% a valószínűsége annak, hogy tíz vásárló között kettő olyan lesz, akik csupa ép tojást tartalmazó dobozt vásároltak.   9. Oldjuk meg az egész számok halmazán a következő egyenletet: $\begin{array}{c}{\displaystyle \left|\frac{x^2+y^2}{x+y}\right|=1.}\end{array}$  (16 pont)   Megoldás. A tört nevezője miatt: $x+y\ne 0$. Az abszolút értéket felbontva két esetet kell vizsgálnunk: I. eset: $\frac{x^2+y^2}{x+y}=1$. Az egyenletet rendezve az $x^2-x+\left(y^2-y\right)=0$, $x$-re másodfokú egyenlet adódik. Akkor van valós gyök, ha $D=1+4y-4y^2\ge 0$. Ez akkor teljesül, ha $\begin{array}{c}{\displaystyle \frac{1-\sqrt[]{2}}{2}\le y\le \frac{1+\sqrt[]{2}}{2}\mathrm{.}}\end{array}$ Mivel $y$ egész szám, így $y=0$ vagy $y=1$ lehet. Ha $y=0$, akkor $x=1$ vagy $x=0$ lehet. Ha $y=1$, akkor $x=1$ vagy $x=0$ lehet. II. eset: $\frac{x^2+y^2}{x+y}=-1$. Az egyenletet rendezve az $x^2+x+\left(y^2+y\right)=0$, $x$-re másodfokú egyenletet kapjuk. Akkor van valós gyöke, ha $D=1-4y-4y^2\ge 0$. Ez akkor teljesül, ha $\begin{array}{c}{\displaystyle \frac{-1-\sqrt[]{2}}{2}\le y\le \frac{-1+\sqrt[]{2}}{2}\mathrm{.}}\end{array}$ Mivel $y$ egész szám, így $y=-1$, vagy $y=0$ lehet. Ha $y=-1$, akkor $x=0$ vagy $x=-1$. Ha $y=0$, akkor $x=0$ vagy $x=-1$. A kikötés figyelembevételével a következő megoldásokat kaptuk: $\begin{array}{c}{\displaystyle \left(1;0\right)\mathrm{,}\left(0;1\right)\mathrm{,}\left(1;1\right)\mathrm{,}\left(\mathrm{0,}-1\right)\mathrm{,}\left(-\mathrm{1,}-1\right)\mathrm{,}\left(-1;0\right)\mathrm{.}}\end{array}$