|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A 42. Nemzetközi Fizikai Diákolimpia feladatainak megoldása
1. feladat. Egy háromtest-probléma és a LISA
1.1. A két tömegpont mozgásegyenlete:
Bármelyik egyenletet rendezve, és felhasználva, hogy a keresett szögsebesség
1.2. A tömeg infinitezimálisan kicsi, ezért gravitációs ereje nem befolyásolja a másik két test mozgását.
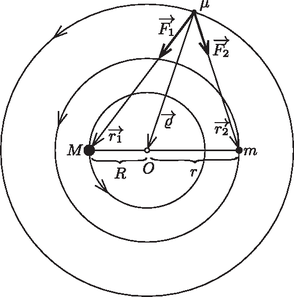 1.ábra
A tömegű testet is a rá ható gravitációs erők eredője tartja körpályán (1. ábra): vagyis | |
Másrészt a tömegközéppont definíciója szerint amit behelyettesítve, és egyszerűsítve | |
A fenti egyenlet két oldalán és együtthatói külön-külön meg kell egyezzenek, ahonnan adódik, vagyis a három test egy szabályos háromszög csúcsain helyezkedik el. A koszinusztétel alapján | |
Ezek szerint
1.2.1. és távolsága: ,
1.2.2. és távolsága: ,
1.2.3. és a tömegközéppont távolsága: .
1.3. A feladat az egyensúlyi helyzet körüli kis rezgések körfrekvenciájának meghatározása volt. Ehhez a versenyzők azt az útmutatást kapták, hogy tételezzék fel a rezgő test perdületének megmaradását. Ebből kiindulva és még az energia megmaradását is felírva hosszas számolás után az eredmény kapható (lásd a http://www.ipho2011.org/contents/problems_solutions honlapon a ,,hivatalos'' megoldást).
Sajnos ez a megoldás hibás! A korlátozott háromtest-problémában (amikor az egyik test tömege elhanyagolhatóan kicsi a másik kettőé mellett) sem a kis test perdülete, sem a mechanikai energiája nem megmaradó mennyiség! Ténylegesen még a vizsgált pont stabilitása sem valósul meg, ha ; márpedig a feladatban a speciális esetet kellett volna vizsgálni. Ekkor a kérdéses pont (a szabályos háromszög egyik csúcspontja) körül egyáltalán nem alakulhatnak ki harmonikus rezgések!
1.4. Az űrhajók egymás körül is szögsebességgel keringenek, így a relatív sebességük ahol a ,,karok'' hossza, pedig a Föld keringési ideje. Behelyettesítve
2. feladat. Elektromosan töltött szappanbuborék
2.1. A szappanbuborék belsejében a nyomás a felületi feszültség miatt nagyobb, mint a külső (atmoszférikus) nyomás: (Ezt az összefüggést pl. a képzeletben félbevágott buborék egyik felére felírt erőegyensúly feltételéből származtathatjuk.)
Az egyesített gáztörvény a levegő intenzív állapotjelzőire így írható fel: Ennek alapján a kérdéses arány:
2.2. A megadott számértékek felhasználásával: | |
(Az eredmény azt mutatja, hogy a felületi feszültség hatására a nyomás igen csekély mértékben növekszik.)
2.3. A buborék lebegésének a feltétele az, hogy a buborékra ható felhajtóerő egyenlő nagyságú a buborék súlyával, ami a szappanhártya és a benne lévő levegő súlyának az összege: | |
Megfelelő átrendezés és a számszerű adatok behelyettesítése után a buborék lebegéséhez szükséges belső hőmérséklet: | |
A lebegéshez a buborékban lévő levegőnek valamivel több, mint -kal melegebbnek kell lennie a külső levegő hőmérsékleténél.
2.4. Miközben a buborék belsejében a hőmérséklet a külső levegő hőmérsékletére csökken, a buborék sugara 0,8%-kal lecsökken, és a szappanhártya vastagsága is megnő. Ezeket a változásokat azonban a feladat szövegében szereplő tanács szerint elhanyagoljuk. Nyugvó levegőben ilyenkor a buborék a talaj felé süllyed. Az sebességgel felfelé áramló levegő akkor akadályozza meg a buborék leesését, ha a Stokes-féle közegellenállási erő megegyezik vagy meghaladja a buborék súlyának és a felhajtóerőnek a különbségét:
Átrendezés után a felfelé áramló levegő sebességére a következő relációt kapjuk:
2.5. A számszerű adatok behelyettesítése után m/s eredmény adódik.
Megjegyezzük, hogy a paraméteres kifejezés második tagja az első tagnál három nagyságrenddel kisebb, vagyis elhanyagolható. Ez is indokolja, hogy a továbbiakban a felületi feszültségből adódó tagokat elhanyagoljuk.
2.6. Elektromosan töltött szappanbuborékok esetén a felületi feszültség hatásához képest fordított nyomáskülönbség alakul ki a buborék belseje és a külső levegő között, mivel a buborék felületén lévő töltések taszítják egymást. Ezt a nyomáskülönbséget jelöljük így: . Ezzel a jelöléssel ; feladatunk az egyenlőség jobb oldalán lévő két tag meghatározása.
Elektromos töltések nélkül (a felületi feszültség hatásának elhanyagolásával) a buborékban a nyomás , és a buborék térfogata a kezdeti sugár köbével, vagyis -bel arányos. Feltöltött buborék esetén a nyomás , a térfogat pedig a megnövekedett sugár köbével, vagyis -bel arányos. Mivel a buborékban lévő levegő hőmérséklete nem változik, így alkalmazhatjuk rá a Boyle‐Mariotte-törvényt, vagyis a nyomás és a térfogat fordított arányosságát:
A töltések következtében fellépő nyomásjárulékot a buborék falánál fellépő átlagos elektromos térerősség és az egységnyi felületre jutó töltés (töltéssűrűség) szorzataként számíthatjuk ki. Az sugarú buborék belsejében a térerősség nulla, közvetlenül a buborék felületén kívül pedig így | |
Másrészt a töltéssűrűség , így az elektromos eredetű nyomáskülönbség: Ugyanez a mennyiség a külső és a belső gáznyomás különbségeként is felírható, tehát | |
ahonnan a keresett kifejezés pl. így adható meg: | |
2.7. Feltételezve, hogy a buborék sugarának megváltozása (az eredeti sugárhoz viszonyítva) kicsi, a fenti formulában az | |
közelítés alkalmazható, s innen a sugár (kicsiny) növekedésére ez adódik:
2.8. A lebegés feltétele most is a felhajtóerő és a súly egyensúlya: | |
Ha a felületi feszültség hatását elhanyagoljuk, akkor a töltetlen buborék belsejében a kezdeti sűrűség megegyezik a külső levegő sűrűségével (), hiszen a hőmérséklet is és a nyomás is (jó közelítéssel) ugyanakkora kívül és belül. A feltöltött buborék sugarát fejezzük ki segítségével: | |
Közelítés és némi egyszerűsítés után ezt kapjuk: | |
Helyettesítsük be helyére az előző alkérdés eredményét, és fejezzük ki a töltést: | |
3. feladat. Ion szóródása semleges atomon
(100 éves a Rutherford-atommodell)
3.1. A Coulomb-törvény alapján az elektromos térerősség a dipólus tengelyén, attól távolságra: | |
Mivel , alkalmazhatjuk a kis -ekre érvényes közelítést: | |
Vektorokkal kifejezésre juttathatjuk a dipólus által keltett térerősség nagyságát és irányát is (a dipól tengelye mentén):
3.2. (Az eredeti ábra jelöléseivel) az ion által a semleges atom helyén létrehozott térerősség a Coulomb-törvény szerint így a neutrális atom nagyságú és irányú elektromos dipólmomentumra tesz szert. A 3.1. alkérdés végeredményét felhasználva ez a dipólmomentum az ion helyén | |
térerősséget hoz létre, így az ionra ható erő: A kifejezésből leolvasható, hogy az erő előjelétől függetlenül mindig a semleges atom felé mutat, vagyis vonzó jellegű.
3.3. Az egymástól távolságra levó ion és atom kölcsönhatási energiája egy előjeltől eltekintve azzal a munkával egyezik meg, amennyit a két részecske ,,végtelen messzire'' történő eltávolítása során végzünk: | |
3.4. A centrális erőtér miatt a mozgó ion perdülete az atom helyére vonatkoztatva megmarad. Amikor az ion legközelebb kerül az atomhoz, a sebességének nagysága maximális, iránya pedig merőleges a helyvektorára, így . A mechanikai energiamegmaradás szerint | |
E két egyenletből a minimális távolságra a | |
egyenletre jutunk, amely -ben másodfokú. Az egyenlet megoldásai: | |
Ha , akkor az ion egyenes pályán, távolságra halad el a semleges atom mellett, így a két gyök közül a nagyobbat kell megtartanunk. Az ion és az atom közötti legkisebb távolság tehát | |
3.5. Ha a impakt paraméter elég nagy, az előző kérdésben kiszámított távolságra közelíti meg az ion az atomot. A paraméter csökkentésével azonban az -re kapott kifejezésben a négyzetgyökjel alatt negatív érték adódik, azaz nincs minimális távolság az ion és az atom között: az ion spirális pályán a semleges atomba csapódik. Ez akkor következik be, ha így az ion befogásának hatáskeresztmetszete | |
Megjegyzés. A 3.4. és 3.5. alkérdésekben tárgyaltak grafikusan is szemléltethetők az ún. effektív potenciál segítségével. Ha az energiamegmaradást kifejező | |
egyenletből a szögsebességet kiküszöböljük a perdületmegmaradás törvényének felhasználásával, akkor a sugár irányú (radiális) mozgásra kapunk egyenletet: A zárójelben álló kifejezést effektív potenciálnak szokták nevezni. a két részecske valódi (vonzó jellegű) kölcsönhatási energiája mellett tartalmaz egy ‐ a perdület nagyságától is függő ‐ taszító (,,centrifugális'') potenciális energiát is.
Az ion-atom távolság időbeli változása éppen úgy zajlik le, mint egy tömegpont egydimenziós mozgása potenciállal megadott erőtérben. (Kicsit erőltetett hasonlattal: ahogy egy golflabda gurul az függvénnyel megadott domborzati viszonyok között.)
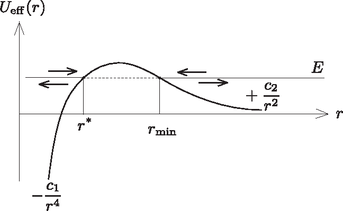 2.ábra
Jelen esetben az effektív potenciál alakú, ahol és a feladatban szereplő paraméterekkel kifejezhető pozitív állandók (2. ábra). A nagy távolságból érkező, energiájú ion radiális sebessége ott válik nullává, ahol Ez a feltétel a korábban kiszámított értéknél és egy ennél kisebb -nál is fennáll. Az ion (ha csak a radiális mozgását nézzük) nyilván távolságnál ,,fordul vissza'', a potenciálhegy tartományába egyáltalán el sem jut. (Érdekes, hogy a kvantumelméletben nem ez a helyzet: a hullámként viselkedő ion ,,át tud bújni'' a potenciálhegy alatt, és még akkor is eljut az atomig, amikor ezt a klasszikus fizika szerint nem tehetné meg. Ez a furcsa jelenség az ún. alagúteffektus.)
Az -os fordulópontnak is van fizikai jelentése: ha az ion nem végtelen messziről, hanem az atom közeléből, az atomtól távolodva indulna, akkor nem tudna tetszőleges messze eljutni, hanem -nál a radiális mozgás visszafordulna (tehát ez az érték lenne az atom és az ion közötti maximális távolság.)
Ha a paraméter (és az ezzel arányos perdület) nem elég nagy, akkor az effektív potenciál maximumának értéke az energia alá kerül. Ilyenkor a messziről érkező részecske ‐ már a klasszikus fizika törvényei szerint is ‐ beleesik az atomba.
1. feladat. Elektromos fekete doboz: kapacitív elmozdulásérzékelő
A mérési feladatban szereplő elektromos fekete doboz egy síkkondenzátor, melynek két, egymás felett elcsúsztatható fémlemeze azonos alakú fogakból áll, melyeket egy vékony szigetelőréteg választ el egymástól.
A kondenzátor kapacitását a versenyzők egy Kipp-oszcillátor segítségével mérhették. A Kipp-oszcillátor egy olyan áramkör, melynek frekvenciáját az összefüggés határozza meg, ahol az oszcillátorra kötött kondenzátor kapacitása, és pedig az eszközre jellemző állandók. Az oszcillátor frekvenciáját digitális multiméterrel lehetett mérni.
A feladat első részében az oszcillátor kalibrálása, azaz és értékének meghatározása volt. Ehhez 4 különböző, ismert kapacitású kondenzátor állt a versenyzők rendelkezésére. Azt is észre kellett venni, hogy a kondenzátorok különböző kapcsolásaival újabb kapacitások is előállíthatók, és így nem csak 4 kalibrációs pontot lehet felvenni. Ha a frekvencia reciprokát a kapacitás függvényében ábrázoljuk, és a pontokra egyenest illesztünk, akkor az egyenes meredeksége , tengelymetszete , így ezek az állandók meghatározhatók.
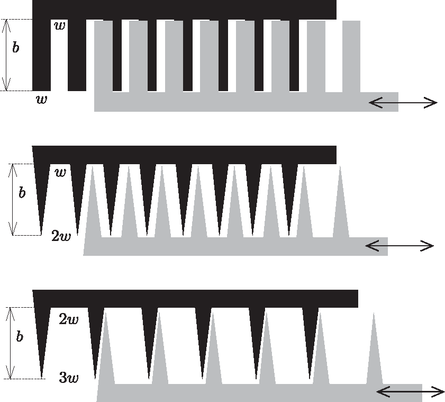 3.ábra
A feladat második részében a síkkondenzátor geometriai alakját kellett meghatározni. A kalibrált Kipp-oszcillátor segítségével meg kellett mérni a kondenzátor kapacitását a mozgatható kondenzátorlemez elmozdulásának függvényében. Az eredmények alapján először el kellett dönteni, hogy a lemezek fogazása milyen. Ehhez megadtak három lehetséges fogalakot (3. ábra), mindegyikhez meg kellett határozni elméleti megfontolások alapján, hogy milyen jellegű függvényt várunk, majd a mérési adatok alapján ki kellett választani, hogy a fekete dobozban milyen fogazás van. Ezek után a kimért függvény alapján meg kellett határozni a fogak geometriai méreteit.
Mivel a Kipp-oszcillátor frekvenciája a mozgatható kondenzátorlemez helyzetétől függ, az eszközt digitális tolómérőként lehet használni. A harmadik részben ennek a digitális tolómérőnek a felbontását kellett kiszámítani, azaz azt a legkisebb elmozdulást, amit az eszközzel még mérni lehet.
2. feladat. Mechanikai fekete doboz: csőben rögzített golyó
A mechanikai fekete doboz egy zárt alumíniumcsőből és egy, a cső belsejében ismeretlen helyen rögzített golyóból állt. A 30 cm hosszú csövön centiméterenként lyukak (összesen 16 db) voltak fúrva, melyek segítségével a csövet vízszintes tengely körüli lengésbe lehetett hozni. A versenyzőknek roncsolásmentes mérésekkel kellett a rendszer olyan tulajdonságait megállapítani, mint a tömegközéppont helye, a cső és a golyó tömegének aránya és a golyó csövön belüli helyzete. Ezen kívül meghatározandó volt a nehézségi gyorsulás értéke is.
Konkrét mérési utasításokat ezúttal nem kaptak a versenyzők, csak a felhasználható eszközök jelenthettek támpontot a mérési módszerek kitalálásában: asztalra rögzíthető tengely a rúd lengetéséhez, vonalzó, stopper, ragasztószalag a tengely asztalra rögzítéséhez, illetve egy méternyi fonál.
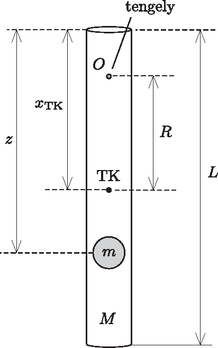 4. ábra
A tömegközéppont helyét a diákok a legkülönbözőbb módokon határozták meg: többen az asztal szélén egyensúlyozták ki a csövet, mások egy vagy két szál fonállal függesztve fel a rendszert azt használták ki, hogy a tömegközéppont mindig a felfüggesztési pont alatt helyezkedik el.
(‐) Nehezebb feladat volt a rúd és a cső tömegarányának, a golyó helyzetének és a nehézségi gyorsulásnak a meghatározása. A kis lengéseket végző cső fizikai ingának tekinthető, melynek lengésideje (a 4. ábra jelöléseit használva) ahol a Steiner-tétel értelmében . A rendszer tömegközéppontra vonatkoztatott tehetetlenségi nyomatéka pedig (a golyóra a pontszerű közelítést alkalmazva): | |
A periódusidő tehát a | |
módon függ a felfüggesztési pont tömegközépponttól mért távolságától. Ez a kifejezés kis átalakítással a alakra hozható. A periódusidőt tehát az távolság függvényében megmérve, majd -et függvényében ábrázolva a mért pontok egy egyenesre illeszkednek, melynek meredekségéből a gravitációs gyorsulást, -ből és a tengelymetszetből pedig a arányt lehet meghatározni. A tömegközéppontra vonatkozó egyenlet felhasználásával a kérdezett tömegarány és a golyó helyzete innen már kiszámolható.
Másik lehetséges eljárás kínálkozik a rendszer paramétereinek meghatározására, ha észrevesszük, hogy a kis lengések periódusideje a felfüggesztési pont helyzetének függvényében egy minimummal rendelkezik. A görbe minimumhelyéből és a minimális lengésidőből ugyancsak kiszámolhatóak a kérdéses mennyiségek, de a lapos minimum miatt ez az eljárás pontatlanabb, mint az elsőként ismertetett módszer, ezért ezt az alternatív megoldást a rendezők csak fele pontszámmal ,,jutalmazták''.
|
Az elméleti feladatok szövegét a múlt havi számunkban közöltük. Megtartottuk az olimpián alkalmazott, a hazai gyakorlattól néhol kicsit eltérő jelöléseket.Ezt legegyszerűbben úgy mutathatjuk meg, ha feltételezzük, hogy a vékony (de véges vastagságú) töltésrétegben a töltések eloszlása homogén. A Gauss-tétel alkalmazásával láthatjuk, hogy ekkor a belső nulla tér lineárisan növekedve éri el a külső felületen felvett értékét, tehát a töltésrétegben átlagosan a külső érték fele lép fel. Megmutatható azonban az is, hogy a vékony töltésrétegben tetszőleges töltéseloszlás esetén is a külső térerősség fele adja az átlagértéket. |
 PDF | MathML
PDF | MathML