|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.
Pali bácsiról szeretnék ezt-azt mesélni. Kezdjük a legelején, volt egy első találkozásunk. Tizenkét éves voltam akkor. Pali bácsi nagyon szerette ezt a találkozást, a velem való találkozását elmesélni, és nagyon sokszor el is mesélte, többen meg is írták, sokszor el is olvastam. És én nem meséltem el még idáig sohasem, vagy legalábbis nem emlékszem rá. Arra gondoltam, hogy ha már egyszer így összejöttünk, akkor most az egyszer ezt én mesélem el. Egyszer talán én is elmesélhetem.
No szóval tizenkét éves voltam. A Múzeum körút 6‐8-ban, a TTK épületében kezdődött a találkozás, ott volt anyám kollégája és barátnője, Péter Rózsi néni, gondolom azért, hogy ne féljek az idegen bácsitól. Meg kell mondanom azonban, hogy egyáltalán nem féltem az idegen bácsitól. Rózsi nénitől talán egy kicsit igen (aki ismerte őt, annak nem kell elmagyaráznom, hogy egy kicsit lehetett tőle félni, bár nagyon szerettem Rózsi nénit, de hát most nem róla akarok mesélni). Ezzel szemben Pali bácsitól egyáltalán nem féltem, éspedig azért nem, mert nem volt benne semmi félelmetes. Nagyon kedves volt, megnyugtató volt a társasága. Azt ugyan nem értettem, miért nevez Epszilonnak, úgyhogy meg is kérdeztem, hogy miért lennék én Epszilon, mire azt felelte, hogy a matematikában így nevezik a kis mennyiségeket. Ezt akkor, tizenkét évesen nem értettem, s emlékszem, egy kicsit tűnődtem azon, hogy mitől kicsi vagy nagy egy mennyiség. Nagyon nem izgathatott, mert nem kérdeztem meg. Az összeismerkedés után, ami egy folyosón történt, elmentünk a Múzeum Kávéházba ebédelni. Ott a leves kanalazása közben, ahogy ezt Pali bácsi sohasem hagyta ki a meséből, föltett nekem egy kérdést:
Az számok közül -et kiválasztottunk. Bizonyítsuk be, hogy van közöttük kettő, amelyek relatív prímek.
Kicsit gondolkoztam rajta, majd azt mondtam, hogy hát ennyi szám között biztosan vannak szomszédosak is. (Ha ezt a számot darab párra szétbontjuk: és számot kiválasztunk az párból, akkor lesz olyan pár, amelyből mind a kettőt ki kell választanunk, s ezek a számok szomszédosak lesznek.) Szomszédos számok pedig mindig relatív prímek.
Hát így történt, ezt mesélte el a Pali bácsi olyan sokszor. El kell árulnom azonban, hogy én erre az egészre nem emlékszem, mindezt csak onnan tudom, hogy olvastam meg hallottam sokszor. Se arra nem emlékszem, hogy ezt Pali bácsi kérdezi, és arra sem, hogy ezen gondolkodom. Kiesett a fejemből. Gyakori, hogy a gyerekek a kiskorukban történteket onnan tudják, hogy a szüleik gyakran el-elmesélik, és végül ez már majdnem olyan, mintha személyes emlék lenne, így vagyok ezzel én is, csak itt a Pali bácsi a mesélő. Ezzel szemben sokkal jobban emlékszem erre a kérdésre:
Az számok közül -et kiválasztottunk. Bizonyítsuk be, hogy biztosan van közöttük osztó és többszörös.
Ugyanúgy kezdődik, szintén kiválasztunk ebből a számból -et, de most azt állítjuk, hogy van közöttük osztó és többszörös, tehát van közöttük két olyan szám, amelyek egyike többszöröse a másiknak. Ez sokkal nehezebb, mint az előző, nem is oldottam meg ott, rögtön az ebéd alatt, néhány napig gondolkoztam, nagyon izgatott ez a kérdés. Még emlékszem a megoldás pillanatára Talán ha lesz idő rá, elmondom a megoldást is. Mindenesetre azt már most mondom, hogy ez Pali bácsi egyik legkedvesebb problémája volt. Nagyon szerette ezt a kérdést. A gólyavári előadásban éppen nem hangzott el, de egyébként sokszor elmesélte.
Milyen volt a kapcsolatom vele? A leglényegesebb az, hogy tökéletesen egyenrangú partnerként kezelt engem, és egyáltalán mindenkit, aki vele kapcsolatba került, tehát ez nem az én személyemnek szólt, a gyerekeket, felnőtteket, és most én azért inkább a gyerekekről beszélek, minden fontoskodás nélkül, minden kivagyiság nélkül teljesen egyenrangú partnernek tekintette, és ez a lényéből fakadt, nem szerep volt, egyszerűen így érezte.
A másik, amit el akarok mondani, és szintén nagyon jellemző Pali bácsi és a gyerekek kapcsolatára, hogy igen korán mondott megoldatlan problémákat. Nem volt nagyon didaktikus, nem törekedett annyira, hogy valamit fölépítsen, gyorsan rátért a megoldatlan problémákra. Ez összefüggésben van az előzővel, tehát a természetével, hát ha egyszer a másik egyenrangú partner, akkor úgy bánok vele, mintha olyan lenne, mint én. Én mit is csinálok, matematikai problémákon gondolkozom, akkor tehát mondom neki azokat, amelyek számomra most épp érdekes problémák, és amiket ő azért képes megérteni.
Most felidézek egy másfajta tanítást. Jártam, kicsivel később Gallai Tiborhoz, akit szintén nagyon szerettem. Gallaihoz hetente egyszer mentem, mindig ugyanabban az időben, mindig megkent zsemlékkel várt, gondosan elkészített zsemlékkel, és feladta a gondosan előkészített feladatokat, a feladatok egymásra épültek, és nem (vagy csak nagyon ritkán) mondott megoldatlan problémákat. Pali bácsival rendszertelenül találkoztam, soha semmilyen zsemlét nem kent meg, a feladatsorai nem voltak igazán felépítettek, elég ötletszerűek voltak, és nagyon gyorsan mondott megoldatlan problémákat.
Elmesélem, hogy miért kaptam ki később gyakran, néha Pali bácsitól és többször Hajnal Andrástól, egy kicsit a gondolkodásmódjukat akarom ezzel bemutatni. Hallottam tőlük roppant érdekes megoldott kérdéseket, és nagyon izgatott, hogy hogyan lehet ezeket megoldani. Igazából egy kérdés nem attól volt számomra kedves elsődlegesen, hogy megoldatlan, hanem hogy szép és érdekes. És ők sokszor mondták, hogy ne ezen gondolkozzál, mert ezt már megcsinálták! Jó, hogy tényleg érdekes és szép, de már megcsinálták. Hanem inkább azon gondolkozzam, amit még nem csináltak meg. Mert azzal lehet a tudományt gazdagítani.
Most sok év után magam is gyerekekkel foglalkozom, nem érzem olyan rettenetesen fontosnak, hogy a gyerek nagyon korán megoldatlan problémákkal találkozzon. Azt fontosnak tartom, hogy kutatási helyzetbe kerüljön, fontos, hogy olyasmi történjen vele, ami egy kutatóval kutatás közben, például hogy nehéz feladaton gondolkozzon. Nem érzem, igazán lényegesnek, hogy ez megoldatlan legyen. Ha megoldatlan problémákat adunk gyerekeknek, nem tudjuk megtervezni a munkájukat, mert mi magunk se tudjuk, hogy mi kell a megoldáshoz. Jobban tervezhető egy kutatási helyzet, ha én tudom, hogy a probléma hogyan oldható meg, és akkor olyan helyzeteket tudok teremteni, amelyek meghatározott irányba visznek, meghatározott módszereket igényelnek, és jól elő is tudom készíteni ezt a pillanatot. Az a fontos, hogy a gyerek fejében milyen folyamatok játszódnak le. Ha egy feladat hasznos, ha a rajta való gondolkodás serkentő, akkor ebből semmit nem von le, hogy már megoldották. Továbbá a matematika bizonyos témáihoz nem is vezet ilyen út, ezeknél a területeknél nagyon-nagyon sokat kell ahhoz tanulni, hogy valaki már abba a helyzetbe kerüljön, hogy megoldatlan problémán gondolkozhasson.
Ettől függetlenül természetesen nagyon jó dolog volt, amit Pali bácsi csinált. Azt mondhatnám az ő módszerét nézve, hogy mégis csak vezet a matematikához királyi út. Valamilyen értelemben ez királyi út volt. Tehát a témakör rendes felépítése nélkül, a részletek szisztematikus átgondolása nélkül egy-egy érdekes feladattal eljutni az aktuális problémákhoz. Nem minden területen lehetséges ez. De hát ő olyan területeken csinálta, ahol lehetséges.
Leveleztem is Pali bácsival. Mutatok néhány olyan feladatot, amit levélben kaptam tőle, azazhogy annyi év után nem tudom már, hogy mi volt ebből levél és mi személyes közlés. Négy probléma, megoldott problémák, természetesen nem csak megoldatlan problémákat mondott Pali bácsi, mondott megoldottakat is, most négy megoldott problémát mutatok.
| 1. | irracionális. |
| 2. | egészek nem lehet egész. |
| 3. | végtelen halmaz. elemei a prímekből épülnek fel létezik egy végtelen osztólánc -ban. |
Csupa érdekes kérdés, talán olyan nagyon nem is kell őket kommentálnom De azért az első feladathoz tegyük hozzá: ezt egy 14-15 éves gyereknek adta föl, aki nem ismerte a végtelen sor összegének fogalmát. És az számról se tudott többet, mint hogy ennek a végtelen összegnek az értéke.
A harmadik feladatban az az érdekes, ahogy a végtelen fogalmát exponálja. Egy végtelen halmazban, természetes számok egy végtelen halmazában van egy végtelen osztólánc, ha ez a halmaz olyan, hogy véges sok prímből épül föl. Ugye, ha végtelen sok prímből épül föl, akkor ez nem igaz, a prímszámok halmazában egyáltalán nincs osztó és többszörös. Tehát az lényeges, hogy végtelen sok eleme van, de ez véges sok prímből épül föl. Ez a feladat nagyon jó, és a végtelenről való gondolkodásnak az ízét, módszerét mutatja. Tehát például egy ilyen feladattal bele lehet lökni valakit abba, hogy mi a véges és a végtelen, és hogyan lehet ezzel bánni. A Ramsey-tétel azt mondja, hogy ha egy végtelen teljes gráf éleit két színnel megszínezzük, akkor lesz benne egy végtelen, teljes, egyszínű részgráf. Ez szintén a véges-végtelennel kapcsolatos első nagy lökések egyike lehetett.
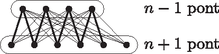
Ahogy erről már beszéltem, Pali bácsi tehát adott megoldott kérdéseket, de nem nagyon szisztematikusan, nem nagyon felépítve, és elég türelmetlenül várta a pillanatot, hogy a számára sokkal kedvesebb megoldatlan problémákra rátérhessen. Hát ilyet nagyon sokat mondott nekem, most egyet bemutatok ezek közül. Először is ismerkedjünk meg a Dirac-tétellel. A Dirac-tétel azt mondja ki, hogy ha egy gráfnak pontja van, és mindegyik pont foka legalább , akkor a gráf tartalmaz Hamilton-kört (azaz olyan kört, amely a gráf minden pontján átmegy).
Minden tétel kapcsán fölmerülhet az élesség problémája. A tétel látszólag éles. Ugyanis ha fölveszünk pontokat két kupacban, az egyikbe -et, a másikba -et teszünk, és a két kupac között minden lehetséges élt behúzunk, akkor most minden pont foka legalább .
A gráf pedig nyilvánvalóan nem tartalmaz Hamilton-kört, hiszen ha elképzeljük a kört, ahogy föl-le lépdelünk a két rész között, akkor a végén láthatóan bajba kerülünk, mert fönt már elfogynak a pontok, amikor lent még nem fogytak el. Így vagy úgy, de mindenki könnyen végiggondolhatja, hogy ebben a gráfban miért nincsen Hamilton-kör.
Tehát akkor úgy látszik, hogy a Dirac-tétel éles. Pali bácsi azonban belevitt ebbe a témakörbe egy egészen új gondolatot, amit nekem rögtön el is mondott, egyébként hát azt nem kell mondanom, hogy hihetetlen képessége volt az érdekes kérdések felvetésére, és ezeket mindig nagyon önzetlenül osztogatta. Nos, azt a kérdést vetette föl Pali bácsi, hogy ha már ilyen frontálisan, minden pontra vonatkozóan a fokszámfeltételt nem is lehet gyengíteni, de talán megengedhetnénk néhány kivételes pontot. Mondjuk, van egy darab másodfokú pont, és a többire áll az eddigi feltétel. Vagy két darab harmadfokú pontot engedélyezünk, a többi pont foka most is legalább legyen. Vagy lehet három kivételes pont is, de legalább negyedfokúak legyenek stb. Ilyen értelemben talán lehetne a Dirac-tételt élesíteni. Akkor nekem nagyon megtetszett ez a gondolat, hogy egy ilyen kevert feltétellel is lehetne próbálkozni, és az előbbi sejtést sikerült bebizonyítanom, sőt egy ennél erősebb állítás is kijött. Ebből lett az első önálló cikkem.
Pali bácsi az év legnagyobb részében külföldön tartózkodott. Ilyenkor leveleztünk, ha pedig Pesten volt, akkor mindennapos telefonkapcsolatban voltunk egymással. Egyébként a leveleiről hadd mondjak annyit, hogy egyszer egy osztálytársam nálam járt, amikor egy levelét kibontottam, és percekig kacagott azon, hogy a levél így kezdődött: ,,Kedves Pósa Lajos! Remélem, jól vagy. Legyen pozitív egész szám '' Szóval nem volt sok cicázás, cicomázás, rátért a lényegre. Így ment mindez egy jó darabig.
Hogy alakult később a kapcsolatunk? Az úgy történt, hogy a későbbiekben is sok problémát mondott nekem, azonban az érdeklődésem irántuk elkezdett csökkenni. Tehát egyre rosszabb partner lettem, kevésbé csillogó szemmel gondolkoztam a kérdésein, és ezt persze észrevette, ritkábban telefonált, és aztán eljött az az idő, amikor Pali bácsi úgy járt Pesten, hogy fel se hívott engem telefonon, tehát már nem érezte fontosnak, hogy beszélgessünk. Múltak az évek, és aztán azért egyszer-egyszer fölhívott ‐ ritkán ‐, és ha valami érdeklődést mutattam a kérdései iránt, mondjuk, visszahívtam, és valamelyik kérdésével kapcsolatban mondtam valamit, akkor nagyon lelkes lett, és ilyenkor előfordult, hogy néhány napig akár naponta négyszer is felhívott telefonon, mert akkor megint azt érezte, hogy valamilyen munkatársi kapcsolat alakulhat ki közöttünk. Ezt szerette volna, és én is szerettem volna, de az élet másként alakult.
Nem volt megelégedve a pályafutásommal. Tanári tevékenységemet nem becsülte sokra. Ez persze engem bosszantott, de erről most nem kívánok többet beszélni. Viszont még szeretnék mesélni két dolgot vele kapcsolatban. Az egyik sok évvel később történt, mint az említettek. Kilenc évvel ezelőtt csináltam egy matematikai tábort gyerekeknek, akik akkor 15 évesek voltak. A színhely egy budapesti kollégium, jelen vannak 15 éves gyerekek, élvonalbeli 15 éves gyerekek, s Pali bácsi éppen Pesten volt. Megkérdeztem, hogy lenne-e kedve eljönni. Volt kedve eljönni. Egyébként nem kellett különösebben udvarolni neki ahhoz, hogy gyerekeket megnézzen vagy gyerekekkel összeismerkedjen, és talán Lovász Laci és Ruzsa Imre majd elmesélik, hogy ők hogyan ismerkedtek meg Pali bácsival. Én már nem emlékszem arra, hogy kik voltak, akiket elvittem Pali bácsihoz, ugyanis annyira természetes volt a számára, hogy ő bárkit megnéz. Már gimnazista koromban is, ha megemlítettem, hogy szeretném elhozni egy barátomat vagy ismerősömet, akit nagyon érdekel a matematika, akkor minden további nélkül mondta, hogy persze, persze, hozd csak el, és így aztán ez nem volt esemény, tehát nem is maradt meg igazán a fejemben.
Így az is természetes volt Pali bácsinak, hogy eljött akkor a 15 éves gyerekekhez, s gondolom, örülni fognak a jelenlévők, ha most bepillantunk abba, hogy mit is csinált kilenc évvel ezelőtt Pali bácsi azon a délutánon. Szerencsére feljegyeztem a feladatokat.
| 1. | Az számok közül legfeljebb hányat lehet kiválasztani úgy, hogy a belőlük képezhető összes összeg különböző legyen? |
| 2. | Minden háromszög egyenlőszárú. |
| 3. | Bármely szám egyenlő. |
| 4. |  |
| és között van prím. |
| és között van prím (megoldatlan). |
| és között van prím (megoldott). |
| , páros felbontható két prím összegére. |
| Van-e végtelen sok ikerprím? |
| Van-e végtelen sok alakú prím? |
| 6. | Adott a síkban 5 pont, amelyek közül nem esik 3 egy egyenesre kiválasztható közülük egy konvex négyszög 4 csúcsa. |
Adott a síkban 9 pont, amelyek közül nem esik 3 egy egyenesre kiválasztható közülük egy konvex ötszög 5 csúcsa.
Sejtés: Adott a síkban pont, amelyek közül nem esik 3 egy egyenesre kiválaszthatók közülük egy konvex -szög csúcsai.
| 7. | Konvex -szögnek mindig van olyan csúcsa, amelytől nincs 4 csúcs azonos távolságra. |
| 8. | nem igaz. |
: Ismert a legkisebb , amelyre igaz.
: Számítógéppel remélhető, hogy megtaláljuk a legkisebbet.
: Számítógéppel sincs sok remény.
| 9. | Gallai-tétel: adott a síkban véges sok pont, amelyek nem esnek egy egyenesre. Ekkor biztosan van olyan egyenes, amely pontosan kettőn megy át az adott pontok közül. |
| 10. | Adott (egész) szám -ig van közöttük osztó és többszörös. |
| 11. | Hány szám -ig van közöttük kettő, , melyre is a számok között van? |
| 12. | Hány szám -ig van közöttük három, , melyre , és is a számok között van? |
Sejtés: . Pali bácsi 1000 Ft-ot ajánlott fel a megoldásért.
Ez az előadás a táborban 1990-ben hangzott el. Ma délután videofelvételen láttuk, hogy mit mondott el Pali bácsi 80 éves korában, 1993-ban a Gólyavárban. Jól láthatók a kedves, fontosnak érzett, visszatérő motívumok. A nyitókérdés ugyebár ugyanaz. De ebben a tábori műsorban ez után mindjárt két olyan dolog következett, ami most engem is meglepett, amikor annyi év után elővettem a feljegyzéseimet. Kicsit bolondozott a gyerekekkel, mutatott két hibás bizonyítást. Egy bizonyítást arra, hogy minden háromszög egyenlőszárú, és levezette, hogy bármely szám egyenlő. Ez teljes indukcióval ment, szerinti teljes indukcióval. Ezek jól ismert tréfák, de ha most nem látnám a füzetemben, nem is gondolnám, hogy ilyenfajta bolondozás is benne volt a repertoárjában.
Kimondta, persze bizonyítás nélkül az Erdős‐Mordell-egyenlőtlenséget (4.). Prímszámokról elmesélte a kedvenc megoldatlan problémákat, de hozzátett két régóta igazolt állítást (5/), természetesen semmit se bizonyítva. A konvex sokszögek kiválasztásának problémájáról az előadásában már sokat hallottunk. A 8. pontban azonban olyasmiről van szó, ami nem szerepelt a gólyavári előadásban, noha ezt a témát is nagyon szerette és gyakran emlegette.
Mit is jelentenek ezek a nyilak? A már említett Ramsey-tétel véges változatairól van szó. például a következő állítást jelenti: ha egy pontból álló teljes gráf éleit két színnel megszínezzük, akkor a gráf tartalmazni fog egy 4-pontú, teljes, egyszínű részgráfot. Érdekes, hogy az utolsó kérdést mennyire reménytelennek tartotta.
A 9. és a 10. állítást nagyon szerette elmesélni. Érdekes kérdések, kerek válaszok. Előadásaiban Pali bácsi viszonylag ritkán mondott bizonyításokat. De ennek a két állításnak szerette elmondani a bizonyítását is. Megvan bennük a matematika varázsa. Nehéz rájönni ezekre a bizonyításokra, de utólag rövidek és gyönyörűek. A 10. feladat megoldását most elmondom.
Helyezzük el az számokat különböző sorokba a következő módon: | |
A sorok egy-egy páratlan számmal kezdődnek, tehát a sorok száma (hiszen páratlan szám van -ig). A megadott szám így nem eshet csupa különböző sorba, tehát van közöttük kettő, amelyek egy sorban vannak. Egy soron belül azonban bármelyik két szám osztó-többszörös viszonyban áll egymással.
Amikor ezt a feladatot Pali bácsi nekem feladta, én nem jöttem rá erre a megoldásra. Van egy sokkal kevésbé szellemes, de könnyebben megtalálható teljes indukciós bizonyítás is.
Még egy történet van hátra, és ez már az utolsó találkozásunkról szól. 1996. nyarán volt az Ifjúsági Matematikai Kongresszus Miskolcon, hat héttel Pali bácsi halála előtt. A főszervező megkért, érjem el valahogyan, hogy Pali bácsi egy előadás erejéig meglátogassa a konferenciát. Most sem volt nehéz dolgom , elég volt néhány szó. Egerben tartottak ugyanabban az időben egy másik konferenciát, onnan jött át Pali bácsi minket meglátogatni.
Szóval eljött, megtartotta az előadást, olyan jellegű volt, mint amilyenekkel ma már találkoztunk. Sajnos nem jegyzeteltem, és így nem tudok beszámolni a részletekről. Az előadás után egy kicsit rosszkedvűnek láttam, odamentem és elmeséltem, hogy van itt a konferencián a résztvevők között két egészen kicsi gyerek, 11-12 évesek, megkérdeztem, hogy lenne-e kedve megismerkedni velük. Egészen felélénkült a gondolattól, mondta, hogy nagyon szívesen találkozna a gyerekekkel. Összehoztam őket egymással, de aztán valamiért el kellett mennem máshová.
Este bankett volt, a résztvevők kisebb termek között oszlottak szét. Kíváncsi lettem, hol van Pali bácsi, abban se voltam biztos, hogy itt van-e még, vagy visszament már Egerbe. Be-benéztem hát a termekbe, és az egyikben meg is találtam. Egy hosszú asztal végénél ült, két oldalán a két kisfiúval. Csendben voltak, nem beszélgettek, addigra Pali bácsi már elfáradhatott. A többiek, akik az asztalnál ültek, felnőttek voltak, zajosak, vidámak, talán néhány pohár bor is lecsúszott már a torkukon, nem vettek tudomást a kisfiúkról és az idős bácsiról. Odamentem, és üdvözöltem őket. Pali bácsi magához tért, odahajolt hozzám, és azt kérdezte: ,,Mondd, feladhatom a gyerekeknek azt, hogy ha adott szám -ig, akkor van köztük osztó és többszörös ?'' ,,Még ne, Pali bácsi ‐ feleltem ‐, talán majd legközelebb ''
|
Természet világa: Természettudományi közlöny, 132. évf. 8. sz., 346‐348. oldal.
http://web.archive.org/web/20100903032406/http://www.sulinet.hu/termeszetvilaga/
archiv/2001/0108/03.html Az előadásom előtt videofelvételről megnéztük Pali bácsi 1993-as gólyavári előadását. A felvétel a 80. születésnap alkalmából készült. Utánam ők tartottak előadást. |
|
 PDF | MathML
PDF | MathML