Cím:	Megoldásvázlatok a 2013/1. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Számadó László
Füzet:	2013/február, 77 - 83. oldal	PDF  |  MathML

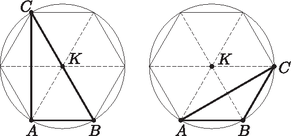
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Egy $r$ sugarú körbe írt $ABC$ háromszögben $AB=r$ és $AC=r\sqrt[]{3}$. Mekkora a $BC$ oldal?  (11 pont)   Megoldás. Az $r$ sugarú kör középpontja legyen a $K$ pont, a keresett $BC$ oldal hossza pedig $x$. Tudjuk, hogy az $AKB$ háromszög szabályos, vagyis az $AB$ (kisebbik) ívhez tartozó $AKB$ középponti szög 60 fokos. Ezért az $ABC$ háromszög $C$ csúcsánál található belső szög 30 fokos, hiszen ez az előbbi ívhez tartozó egyik kerületi szög. Írjuk fel az $ABC$ háromszögre a koszinusztételt: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle r^2}& {\displaystyle =x^2+{\left(r\sqrt[]{3}\right)}^2-2\sqrt[]{3}\cdot r\cdot x\cdot \text{cos}{30}^{\circ }\mathrm{,}}\hfill \\ \hfill {\displaystyle r^2}& {\displaystyle =x^2+3r^2-2\sqrt[]{3}\cdot r\cdot x\cdot \frac{\sqrt[]{3}}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle =x^2-3rx+2r^2\mathrm{.}}\hfill \end{array}}$ Oldjuk meg ezt az $x$-re másodfokú egyenletet: $\begin{array}{c}{\displaystyle x_{1;2}=\frac{3r\pm \sqrt[]{9r^2-8r^2}}{2}=\frac{3r\pm r}{2}\mathrm{.}}\end{array}$ Vagyis $x_1=2r$, $x_2=r$.     A $BC$ oldal lehetséges hossza: $2r$ vagy $r$.   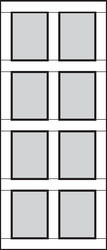2. Egy 90 cm széles és 210 cm magas, kazettás ajtó vázlatát mutatja az ábra.     A nyolc egyforma téglalap alakú kazetta pontosan az ajtó lapjának a felét teszi ki. A kazetták közötti és melletti sávok szélessége mindenütt ugyanannyi. Mekkora ez a szélesség?  (13 pont)   Megoldás. A sávok szélessége legyen $x$. A rajzon látható darabolás segítségével felírjuk a kazettákon kívüli rész területét, ami az ajtólap területének felével egyenlő: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 5\cdot 90\cdot x+3\cdot x\cdot \left(210-5\cdot x\right)}& {\displaystyle =\mathrm{9450,}}\hfill \\ \hfill {\displaystyle 450x+630x-15x^2}& {\displaystyle =\mathrm{9450,}}\hfill \\ \hfill {\displaystyle x^2-72x+630}& {\displaystyle =0.}\hfill \end{array}}$ Megoldóképlettel a gyökök: $\begin{array}{c}{\displaystyle x_{1;2}=\frac{72\pm \sqrt[]{2664}}{2}\mathrm{,}\text{azaz}{x}_1\approx 10\mathrm{,}\mathrm{2,}{x}_2\approx 61\mathrm{,}8.}\end{array}$ Mivel az ajtó szélessége 90 cm, azért a sávok szélessége kisebb, mint 30 cm. Vagyis a kapott gyökök közül csak az $x_1$ felelhet meg. Tehát az ajtón a kazetták körüli sávok kb. 10,2 cm szélesek.   3. Oldjuk meg a következő egyenletet: $\begin{array}{c}{\displaystyle \left(x-5-2\sqrt[]{x-2}\right)\left(x-10-4\sqrt[]{x-5}\right)=0.}\end{array}$ (13 pont)   Megoldás. Az egyenlet értelmezési tartománya: $x\ge 5$. Az egyenletet a következő alakra hozhatjuk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \left(x-2-2\sqrt[]{x-2}-3\right)\left(x-5-4\sqrt[]{x-5}-5\right)}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle [{\left(\sqrt[]{x-2}\right)}^2-2\sqrt[]{x-2}-3]\cdot [{\left(\sqrt[]{x-5}\right)}^2-4\sqrt[]{x-5}-5]}& {\displaystyle =0.}\hfill \end{array}}$ Az első tényező $\sqrt[]{x-2}$-re, a második tényező pedig $\sqrt[]{x-5}$-re másodfokú. Ezeket a másodfokúnak tekinthető tényezőket tovább bonthatjuk, így kapjuk a következő alakot: $\begin{array}{c}{\displaystyle \left(\sqrt[]{x-2}-3\right)\left(\sqrt[]{x-2}+1\right)\left(\sqrt[]{x-5}-5\right)\left(\sqrt[]{x-5}+1\right)=0.}\end{array}$ Egy szorzat akkor nulla, ha legalább egy tényezője nulla. A második és a negyedik tényező nem lehet 1-nél kisebb, vagyis ezek semmilyen $x$ esetén sem lesznek nullák. Marad két eset. I. eset: $\sqrt[]{x-2}-3=0$. Ekkor $x=11$. II. eset: $\sqrt[]{x-5}-5=0$. Ekkor $x=30$. Mindkettő megoldás, mert benne van az értelmezési tartományban. 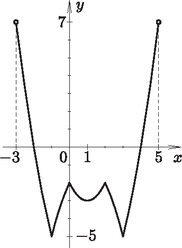(Könnyen ellenőrizhető is a gyökök helyessége.)   4. Adott az $f:\left]-3;5\right[\to \text{R}$, $f\left(x\right)=||{\left(x-1\right)}^2-1|-3|-5$ függvény. $a)$ Adjuk meg a függvény zérushelyeit. $b)$ Adjuk meg azon rácspontok koordinátáját, amelyek illeszkednek a függvény grafikonjára. $c)$ Mely intervallumokon szigorúan monoton csökkenő a függvény?  (14 pont)   Megoldás. $a)$ Az $||{\left(x-1\right)}^2-1|-3|-5=0$ egyenlet megoldásait keressük. Az $|{\left(x-1\right)}^2-1|-3$ lehet $-5$ vagy 5, azaz: $\begin{array}{c}{\displaystyle |{\left(x-1\right)}^2-1|=-2\text{vagy}|{\left(x-1\right)}^2-1|=8.}\end{array}$ Természetesen az első egyenlet nem teljesülhet semmilyen valós $x$-re sem. Vagyis csak az ${\left(x-1\right)}^2=9$ adhat megoldást. (Az ${\left(x-1\right)}^2=-7$ sem teljesülhet.) Innen pedig: $x_1=-2$, $x_2=4$. $b)$ A függvény értelmezési tartományában hét egész szám található. Ezek a $-2$, $-1$, 0, 1, 2, 3 és a 4. Vagyis hétnél több rácspont nem illeszkedhet a függvény grafikonjára. Kiszámítjuk ezeken a helyeken a függvényértékeket. Mivel mindegyik esetben egész számot kapunk, azért a feltételeknek megfelelő rácspontok a következők: $\left(-2;0\right)$, $\left(-1;-5\right)$, $\left(0;-2\right)$, $\left(1;-3\right)$, $\left(2;-2\right)$, $\left(3;-5\right)$ és $\left(4;0\right)$.     $c)$ A normálparabola transzformálásával a függvény képe megrajzolható. A $\left]-3;-1\right]$, $\left[0;1\right]$ és a $\left[2;3\right]$ intervallumokon a függvény szigorúan monoton csökkenő.   II. rész     5. Az $a$, $b$ és $c$ pozitív számjegyekről a következőket tudjuk: $a+b+c=\overline{ab}$ és $a^2+b^2+c^2=\overline{b^{2}a}$ (ahol $\overline{ab}$ és $\overline{b^{2}a}$ is egy-egy kétjegyű szám). Adjuk meg ezeket a számjegyeket.  (16 pont)   Megoldás. A feladat szövegéből kiderül, hogy $b$ olyan pozitív számjegy, amelynek a négyzete is számjegy. Vagyis összesen három eset van. I. eset: Ha $b=3$, akkor az $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle a+3+c}& {\displaystyle =10a+3}\hfill \\ \hfill {\displaystyle a^2+9+c^2}& {\displaystyle =90+a}\hfill \end{array}}\}}\end{array}$ egyenletrendszert kell megoldanunk, amit a következő alakban is írhatunk: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle c}& {\displaystyle =9a}\hfill \\ \hfill {\displaystyle a^2+c^2}& {\displaystyle =a+81}\hfill \end{array}}\}\mathrm{.}}\end{array}$ Az $a$ olyan pozitív számjegy, amelynek a kilencszerese is számjegy. Vagyis $a=1$, $c=9$. Ez valóban megoldás, mert az egyenletrendszer második egyenletét is igazzá teszi. II. eset: Ha $b=2$, akkor az $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle a+2+c}& {\displaystyle =10a+2}\hfill \\ \hfill {\displaystyle a^2+4+c^2}& {\displaystyle =40+a}\hfill \end{array}}\}}\end{array}$ egyenletrendszert kell megoldanunk, amit a következő alakban is írhatunk: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle c}& {\displaystyle =9a}\hfill \\ \hfill {\displaystyle a^2+c^2}& {\displaystyle =a+36}\hfill \end{array}}\}\mathrm{.}}\end{array}$ Most is csak az $a=1$, $c=9$ adódna az első egyenletből, de ez nem megoldása a második egyenletnek. III. eset: Ha $b=1$, akkor az $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle a+1+c}& {\displaystyle =10a+1}\hfill \\ \hfill {\displaystyle a^2+1+c^2}& {\displaystyle =10+a}\hfill \end{array}}\}}\end{array}$ egyenletrendszert kell megoldanunk, amit így írhatunk: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle c}& {\displaystyle =9a}\hfill \\ \hfill {\displaystyle a^2+c^2}& {\displaystyle =a+9}\hfill \end{array}}\}\mathrm{.}}\end{array}$ Az előző esethez hasonlóan innen sem kapunk megfelelő számjegyeket. A feladat egyedüli megoldása: $a=1$, $b=3$, $c=9$.   6. 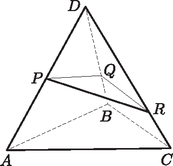Az $ABCD$ szabályos tetraédert egy síkkal elmetsszük. A metszősík három, egy csúcsból induló élt metsz a közös csúcstól számítva $1:1$, $2:1$ és $3:1$ arányban. Határozzuk meg a lemetszett tetraéder és az eredeti tetraéder felszínarányát.  (16 pont)   Megoldás. Használjuk az ábra jelöléseit. Tudjuk, hogy $DP:PA=1:1$, $DQ:QB=2:1$, $DR:RC=3:1$. Legyen a szabályos tetraéder élhossza $a$, ekkor $PD=\frac{a}{2}$, $QD=\frac{2a}{3}$, $RD=\frac{3a}{4}$.     Az $ABCD$ szabályos tetraéder felszíne: $\begin{array}{c}{\displaystyle A_{ABCD}=a^2\cdot \sqrt[]{3}\mathrm{.}}\end{array}$ A lemetszett tetraéder oldallapjainak egyik szöge 60 fokos, ezt felhasználva felírható mindhárom háromszögnek a területe: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle t_{PQD}}& {\displaystyle =\frac{\frac{a}{2}\cdot \frac{2a}{3}\cdot \text{sin}{60}^{\circ }}{2}=\frac{\frac{a^2}{3}\cdot \frac{\sqrt[]{3}}{2}}{2}=\frac{a^2\cdot \sqrt[]{3}}{12}\approx 0\mathrm{,}144\cdot a^2\mathrm{,}}\hfill \\ \hfill {\displaystyle t_{QRD}}& {\displaystyle =\frac{\frac{2a}{3}\cdot \frac{3a}{4}\cdot \text{sin}{60}^{\circ }}{2}=\frac{\frac{a^2}{2}\cdot \frac{\sqrt[]{3}}{2}}{2}=\frac{a^2\cdot \sqrt[]{3}}{8}\approx 0\mathrm{,}217\cdot a^2\mathrm{,}}\hfill \\ \hfill {\displaystyle t_{RPD}}& {\displaystyle =\frac{\frac{3a}{4}\cdot \frac{a}{2}\cdot \text{sin}{60}^{\circ }}{2}=\frac{\frac{3a^2}{8}\cdot \frac{\sqrt[]{3}}{2}}{2}=\frac{3a^2\cdot \sqrt[]{3}}{32}\approx 0\mathrm{,}162\cdot a^2\mathrm{.}}\hfill \end{array}}$ A lemetszett tetraéder alsó lapjának minden oldalhossza koszinusztétellel meghatározható: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P{Q}^2}& {\displaystyle ={\left(\frac{a}{2}\right)}^2+{\left(\frac{2a}{3}\right)}^2-2\cdot \frac{a}{2}\cdot \frac{2a}{3}\cdot \text{cos}{60}^{\circ }=\frac{a^2}{4}+\frac{4a^2}{9}-\frac{a^2}{3}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\begin{array}{c}\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>9</mn><mrow><msup><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">+</mo><mn>16</mn><mrow><msup><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">-</mo><mn>12</mn><mrow><msup><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></mrow><mrow><mn>36</mn></mrow></mfrac></mrow><mo stretchy="false">=</mo><mrow><mfrac><mrow><mn>13</mn><mrow><msup><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></mrow><mrow><mn>36</mn></mrow></mfrac></mrow><mn>,</mn></math>}\end{array}PQ=\frac{a\sqrt[]{13}}{6}\approx 0\mathrm{,}601\cdot a\mathrm{,}}\hfill \\ \hfill {\displaystyle Q{R}^2}& {\displaystyle ={\left(\frac{2a}{3}\right)}^2+{\left(\frac{3a}{4}\right)}^2-2\cdot \frac{2a}{3}\cdot \frac{3a}{4}\cdot \text{cos}{60}^{\circ }=\frac{4a^2}{9}+\frac{9a^2}{16}-\frac{a^2}{2}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\begin{array}{c}\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>64</mn><mrow><msup><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">+</mo><mn>81</mn><mrow><msup><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">-</mo><mn>72</mn><mrow><msup><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></mrow><mrow><mn>144</mn></mrow></mfrac></mrow><mo stretchy="false">=</mo><mrow><mfrac><mrow><mn>73</mn><mrow><msup><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></mrow><mrow><mn>144</mn></mrow></mfrac></mrow><mn>,</mn></math>}\end{array}QR=\frac{a\sqrt[]{73}}{12}\approx 0\mathrm{,}712\cdot a\mathrm{,}}\hfill \\ \hfill {\displaystyle R{P}^2}& {\displaystyle ={\left(\frac{3a}{4}\right)}^2+{\left(\frac{a}{2}\right)}^2-2\cdot \frac{3a}{4}\cdot \frac{a}{2}\cdot \text{cos}{60}^{\circ }=\frac{9a^2}{16}+\frac{a^2}{4}-\frac{3a^2}{8}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\begin{array}{c}\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mn>9</mn><mrow><msup><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">+</mo><mn>4</mn><mrow><msup><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">-</mo><mn>6</mn><mrow><msup><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></mrow><mrow><mn>16</mn></mrow></mfrac></mrow><mo stretchy="false">=</mo><mrow><mfrac><mrow><mn>7</mn><mrow><msup><mrow><mi>a</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></mrow><mrow><mn>16</mn></mrow></mfrac></mrow><mn>,</mn></math>}\end{array}RP=\frac{a\sqrt[]{7}}{4}\approx 0\mathrm{,}661\cdot a\mathrm{.}}\hfill \end{array}}$ A $PQR$ háromszög területét az oldalak ismeretében a Heron-képlettel számolhatjuk ki. Ehhez szükségünk van a háromszög kerületének felére: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle s}& {\displaystyle =\frac{0\mathrm{,}601a+0\mathrm{,}712a+0\mathrm{,}661a}{2}=0\mathrm{,}987a\mathrm{.}}\hfill \\ \hfill {\displaystyle t_{PQR}}& {\displaystyle =\sqrt[]{s\left(s-PQ\right)\left(s-QR\right)\left(s-RP\right)}=\sqrt[]{0\mathrm{,}987a\cdot 0\mathrm{,}386a\cdot 0\mathrm{,}275a\cdot 0\mathrm{,}326a}\approx 0\mathrm{,}185\cdot a^2\mathrm{.}}\hfill \end{array}}$ A lemetszett tetraéder felszínét a négy háromszög területösszege adja: $\begin{array}{c}{\displaystyle A_{PQRD}=0\mathrm{,}144a^2+0\mathrm{,}217a^2+0\mathrm{,}162a^2+0\mathrm{,}185a^2=0\mathrm{,}708a^2\mathrm{.}}\end{array}$ A felszínek keresett aránya a következő: $\begin{array}{c}{\displaystyle \frac{A_{PQRD}}{A_{ABCD}}=\frac{0\mathrm{,}708\cdot a^2}{\sqrt[]{3}\cdot a^2}\approx 0\mathrm{,}41.}\end{array}$   7. Oldjuk meg a valós számok halmazán a $\begin{array}{c}{\displaystyle \text{sin}{}^{4}x+\text{sin}{}^4\left(x+\frac{\pi }{4}\right)+\text{sin}{}^4\left(x-\frac{\pi }{4}\right)=\frac{3}{2}}\end{array}$ egyenletet.  (16 pont)   Megoldás. Mindkét oldalt szorozzuk meg 4-gyel, és írjuk a következő alakban az egyenletet: $\begin{array}{c}{\displaystyle {\left(2\text{sin}{}^{2}x\right)}^2+{\left[2\text{sin}{}^2\left(x+\frac{\pi }{4}\right)\right]}^2+{\left[2\text{sin}{}^2\left(x-\frac{\pi }{4}\right)\right]}^2=6.}\end{array}$ Tudjuk, hogy: $\begin{array}{c}{\displaystyle 2\text{sin}{}^{2}x=\left(\text{cos}{}^{2}x+\text{sin}{}^{2}x\right)-\left(\text{cos}{}^{2}x-\text{sin}{}^{2}x\right)=1-\text{cos}2x\mathrm{.}}\end{array}$ Ezt felhasználva: $\begin{array}{c}{\displaystyle 2\text{sin}{}^2\left(x+\frac{\pi }{4}\right)=1-\text{cos}\left(2x+\frac{\pi }{2}\right)=1+\text{sin}2x\mathrm{,}}\end{array}$ illetve: $\begin{array}{c}{\displaystyle 2\text{sin}{}^2\left(x-\frac{\pi }{4}\right)=1-\text{cos}\left(2x-\frac{\pi }{2}\right)=1-\text{sin}2x\mathrm{.}}\end{array}$ Ezeket a helyettesítéseket alkalmazzuk az eredeti egyenletünkben: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle {\left(1-\text{cos}2x\right)}^2+{\left(1+\text{sin}2x\right)}^2+{\left(1-\text{sin}2x\right)}^2=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =}\hfill & {\displaystyle 1-2\text{cos}2x+\text{cos}{}^{2}2x+1+2\text{sin}2x+\text{sin}{}^{2}2x+1-2\text{sin}2x+\text{sin}{}^{2}2x=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =}\hfill & {\displaystyle \text{sin}{}^{2}2x-2\text{cos}2x+4=6.}\hfill \end{array}}$ Tovább alakítva másodfokú egyenletet kapunk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 1-\text{cos}{}^{2}2x-2\text{cos}2x+4}& {\displaystyle =\mathrm{6,}}\hfill \\ \hfill {\displaystyle \text{cos}{}^{2}2x+2\text{cos}2x+1}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle {\left(\text{cos}2x+1\right)}^2}& {\displaystyle =0.}\hfill \end{array}}$ Azaz $\text{cos}2x=-1$, amiből a $2x=\pi +2k\pi$ (ahol $k\in \text{Z})$ adódik. Az egyenlet megoldásai: $x=\frac{\pi }{2}+k\pi$ (ahol $k\in \text{Z})$.   8. Tekintsük az $y=\left(p-1\right)x^2+2x-\left(p+1\right)$ egyenletű parabolákat, ahol $p$ valós paraméter és $p\ne 1$. $a)$ Melyek ezek közül azok a parabolák, amelyek az $x$ tengelyt két, egész koordinátájú pontban metszik, vagy egy egész koordinátájú pontban érintik? $b)$ Írjuk fel $p=2$ paraméter esetén a parabola 4 abszcisszájú pontján átmenő érintő egyenletét. $c)$ Határozzuk meg a $p=3$ paraméter esetén az $\left[1;3\right]$ intervallumon a parabola alatti terület nagyságát.  (16 pont)   Megoldás. $a)$ Meg kell határoznunk az $\left(p-1\right)x^2+2x-\left(p+1\right)=0$ paraméteres, másodfokú egyenlet zérushelyeit: $\begin{array}{c}{\displaystyle x_{1;2}=\frac{-2\pm \sqrt[]{4+4\left(p-1\right)\left(p+1\right)}}{2\left(p-1\right)}=\frac{-2\pm 2p}{2\left(p-1\right)}=\frac{-1\pm p}{p-1}\mathrm{.}}\end{array}$ Vagyis a zérushelyek: $x_1=1$, $x_2=\frac{-p-1}{p-1}$. (Természetesen $p=0$ esetén $x_1=x_2$.) Csak azt kell megvizsgálnunk, hogy az $x_2$ milyen paraméterek esetén lesz egész, hiszen az $x_1$ mindig egész. Végezzük el a következő átalakításokat: $\begin{array}{c}{\displaystyle x_2=\frac{-p-1}{p-1}=\frac{-\left(p-1\right)-2}{p-1}=-1-\frac{2}{p-1}\mathrm{.}}\end{array}$ A $p-1$ a 2 osztója kell, hogy legyen, vagyis a lehetséges értékei: $-2$, $-1$, 1, 2. Ezek alapján $p$-re négy megfelelő számot kapunk: $-1$, 0, 2, 3. A feladat feltételeinek eleget tevő parabolák: $\begin{array}{c}{\displaystyle y=-2x^2+2x\mathrm{,}y=-x^2+2x-\mathrm{1,}y=x^2+2x-\mathrm{3,}y=2x^2+2x-4.}\end{array}$ $b)$ A $p=2$ paraméter esetén a parabola egyenlete a következő lesz: $\begin{array}{c}{\displaystyle y=x^2+2x-3.}\end{array}$ Tudjuk, hogy az érintő meredekségét minden helyen a derivált adja: $\begin{array}{c}{\displaystyle \left(x^2+2x-3\right)\text{'}=2x+2.}\end{array}$ Vagyis a 4 abszcisszájú pontban $2\cdot 4+2$, azaz 10 lesz az érintő meredeksége. A 4-es abszcisszához $4^2+2\cdot 4-3=21$-es ordináta tartozik. Vagyis a $\left(4;21\right)$ koordinátájú ponton áthaladó 10-es meredekségű egyenes lesz a keresett érintő: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle y-21}& {\displaystyle =10\cdot \left(x-4\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle y}& {\displaystyle =10x-19.}\hfill \end{array}}$ $c)$ A $p=3$ paraméter esetén a parabola egyenlete a következő lesz: $\begin{array}{c}{\displaystyle y=2x^2+2x-4.}\end{array}$ A görbe alatti területet a következő határozott integrál adja: $\begin{array}{c}{\displaystyle \underset{1}{\overset{3}{\int }}\left(2x^2+2x-4\right)dx={\left[2\cdot \frac{x^3}{3}+2\cdot \frac{x^2}{2}-4x\right]}_1^3=18+9-12-\frac{2}{3}-1+4=\frac{52}{3}\mathrm{.}}\end{array}$ Vagyis a $p=3$ paraméter esetén az $\left[1;3\right]$ intervallumon a parabola alatti terület $\frac{52}{3}$.   9. Három különböző egyenes körkúpról tudjuk, hogy az alapköreik sugara és a kúpok alkotói rendre egy-egy azonos differenciájú számtani sorozat három egymást követő elemét adják. Mutassuk meg, hogy a kúpok felszíne nem lehet egy számtani sorozat három egymást követő eleme.  (16 pont)   Megoldás. Az alapkörök sugarai legyenek: $r-d$, $r$, $r+d$, az alkotók pedig: $a-d$, $a$, $a+d$. Ekkor a három kúp felszíne: $\begin{array}{c}{\displaystyle A_1=\pi \left(r-d\right)\left(a-d+r-d\right)\mathrm{,}{A}_2=\pi r\left(a+r\right)\mathrm{,}{A}_3=\pi \left(r+d\right)\left(a+d+r+d\right)\mathrm{.}}\end{array}$ Ha $A_1$, $A_2$, $A_3$ egy számtani sorozat három egymást követő eleme lenne, akkor az $A_3-A_2=A_2-A_1$ egyenlőségnek kellene teljesülnie. Számoljuk ki ezeket a különbségeket: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle A_3-A_2}& {\displaystyle =\pi \left(r+d\right)\left(a+r+2d\right)-\pi r\left(a+r\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\pi \left(ar+ad+r^2+rd+2rd+2d^2-ar-r^2\right)=\pi \left(ad+3rd+2d^2\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle A_2-A_1}& {\displaystyle =\pi r\left(a+r\right)-\pi \left(r-d\right)\left(a+r-2d\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\pi \left(ar+r^2-ar+ad-r^2+rd+2rd-2d^2\right)=\pi \left(ad+3rd-2d^2\right)\mathrm{.}}\hfill \end{array}}$ Látható, hogy a két különbség csak $d=0$ esetén lehetne egyenlő, de a kúpok különbözőek, ezért $d\ne 0$. Vagyis a kúpok felszíne nem lehet egy számtani sorozat három egymást követő eleme.