Cím:	Megoldásvázlatok a 2013/8. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Számadó László
Füzet:	2013/december, 529 - 537. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldásvázlatok a 2013/8. sz. emelt szintű gyakorló feladataihoz   Számadó László   I. rész     1. Két konvex sokszög közül az elsőnek $540$-nel több átlója van, mint a másodiknak, és az elsőnek háromszor annyi csúcsa van, mint a másodiknak. Hány csúcsuk van külön-külön?  (11 pont)   Megoldás. Legyen a második sokszög csúcsainak száma $n$, az elsőé pedig $3n$. Ekkor a feladat szövege szerint: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{3n\left(3n-3\right)}{2}-\frac{n\left(n-3\right)}{2}}& {\displaystyle =\mathrm{540,}}\hfill \\ \hfill {\displaystyle 9n^2-n^2-9n+3n}& {\displaystyle =\mathrm{1080,}}\hfill \\ \hfill {\displaystyle 4n^2-3n-540}& {\displaystyle =0.}\hfill \end{array}}$ Használjuk a megoldóképletet: $\begin{array}{c}{\displaystyle n_{1;2}=\frac{3\pm \sqrt[]{9-4\cdot 4\cdot \left(-540\right)}}{8}=\frac{3\pm 93}{8}\mathrm{.}}\end{array}$ Csak a pozitív egész megoldás jöhet szóba, vagyis $n=12$. Tehát az elsőnek 36, a másodiknak 12 csúcsa van.   2. A miskolci pályaudvar utasellátó büféjének ajtaján a következő tájékoztató szöveg olvasható:   Nyitva tartás 03.30‐23.30. Műszakátadás miatt 07.30‐08.30 és 19.30‐20.30 között zárva!   $a)$ Mekkora eséllyel találjuk nyitva a büfét, ha reggel $7$ és este $9$ között véletlenszerűen érkezünk a bejáratához? $b)$ Egy vargabélest vásároltunk 200 Ft-ért. A pénzt pontosan kiszámolva adtuk át a pénztárosnak. Hányféleképpen tehettük ezt meg, ha 20 Ft-osnál kisebb címletet nem adtunk, és a sorrend nem számít? $c)$ Az utánunk következő vásárló három péksüteményt szeretne venni, a kínálat: diós búrkifli, ízes levél, túrós táska, meggyes rétes és kakaós csiga. Mekkora eséllyel találjuk el, hogy mit fog vásárolni, ha azt feltételezzük, hogy mindegyik választásának ugyanannyi az esélye?  (12 pont)   Megoldás. $a)$ A vizsgált időszakot számegyenesen a $\left[7;21\right]$ intervallummal szemléltethetjük. Ennek az intervallumnak a hossza 14. Műszakátadás miatt ebben az időszakban összesen 2 órát zárva van a büfé. Vagyis a kedvező pillanatokat ábrázolva a számegyenesen három darab, összesen 12 hosszúságú szakaszt kapunk.     A keresett valószínűség ezek alapján: $p=\frac{12}{14}=\frac{6}{7}$. $b)$ A felhasználható pénzérmék értéke: 200, 100, 50, 20. Vizsgáljuk az eseteket az átadott pénzérmék közötti legnagyobb értékű alapján. Ha a legnagyobb érme értéke 200 Ft, akkor az esetek az érmék értékének felsorolásával: $\begin{array}{c}{\displaystyle 200.}\end{array}$ Ha a legnagyobb érme értéke 100 Ft, akkor az esetek az érmék értékének felsorolásával: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle 100+\mathrm{100,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle 100+50+\mathrm{50,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle 100+20+20+20+20+20.}\hfill \end{array}}$ Ha a legnagyobb érme értéke 50 Ft, akkor az esetek az érmék értékének felsorolásával: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle 50+50+50+\mathrm{50,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle 50+50+20+20+20+20+20.}\hfill \end{array}}$ Ha a legnagyobb érme értéke 20 Ft, akkor az esetek az érmék értékének felsorolásával: $\begin{array}{c}{\displaystyle 20+20+20+20+20+20+20+20+20+20.}\end{array}$ Vagyis hétféleképpen tehettük meg a 200 Ft kifizetését. $c)$ A következő vevő 5-féle péksüteményből választhat. Mivel a feladat szövege nem tiltja, azért egy péksüteményből akár többet is vehet. Ha egyféléből hármat venne, az 5 eset. Ha egyféléből kettőt venne, az 20 eset, hiszen 5-féleképpen választhatja ki, hogy melyikből vesz kettőt, majd a maradék négy bármelyikéből vásárolhat még egyet a két azonoshoz.   Ha semelyikből nem venne egynél többet, az $\left(\genfrac{}{}{0ex}{}{5}{3}\right)$, azaz 10 eset. Ez összesen 35 eset. Vagyis $\frac{1}{35}$ eséllyel találhatjuk el, hogy mit fog vásárolni az utánunk következő vásárló. Megjegyzés. Ha ismerjük az ismétléses kombinációk számára vonatkozó képletet, akkor az összes esetek számát azonnal megkaphatjuk:   $C_n^k\left(\text{ism}\right)=\left(\genfrac{}{}{0ex}{}{n+k-1}{k}\right)$. Jelen esetben: $C_5^3\left(\text{ism}\right)=\left(\genfrac{}{}{0ex}{}{5+3-1}{3}\right)=35$.   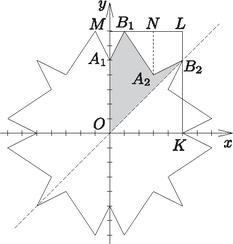3. Adott a koordinátarendszerben négy pont: $A_1\left(0;5\right)$, $B_1\left(1;7\right)$, $A_2\left(3;4\right)$, $B_2\left(5;5\right)$. Tudjuk, hogy $A_1{A}_2$ és $B_1{B}_2$ két koncentrikus kör egy-egy húrja. $a)$ Hol van a körök közös középpontja? $b)$ Tükrözzük az $A_1{B}_1{A}_2{B}_2$ töröttvonalat az első negyed szögfelezőjére, majd az eredeti és a képként kapott alakzatot tükrözzük mindkét tengelyre és az origóra is. Mekkora az így kapott sokszög kerülete, területe?  (14 pont)   Megoldás. $a)$ A körök közös középpontja illeszkedik az $A_1{A}_2$ húrnak az $f_1$ felezőmerőlegesére és a $B_1{B}_2$ húrnak az $f_2$ felezőmerőlegesére is. Vagyis ennek a két egyenesnek kell meghatároznunk a metszéspontját. Az $A_1{A}_2$ felezőpontja: $F_1(\frac{3}{2};\frac{9}{2})$, az $f_1$ egyik normálvektora: $\overrightarrow{A_1{A}_2}\left(3;-1\right)$. Vagyis az $f_1$ egyenes egyenlete: $3x-y=0$. A $B_1{B}_2$ felezőpontja: $F_2\left(3;6\right)$, az $f_2$ egyik normálvektora: $\overrightarrow{B_1{B}_2}\left(4;-2\right)$. Vagyis az $f_2$ egyenes egyenlete: $4x-2y=0$. Mindkét egyenes origóra illeszkedő, tehát az origó a körök közös középpontja. $b)$ Használjuk az ábra jelöléseit. Az $O{A}_1{B}_1{A}_2{B}_2$ ötszög területe az első negyed szögfelezőjére (az $O{B}_2$ oldalegyenesre) történő tükrözés után duplázódik. Az összes tükrözés után pedig ennek az ötszögnek a területe nyolcszorozódik.     Az $O{A}_1{B}_1{A}_2{B}_2$ ötszög $t$ területét megkaphatjuk, ha az $OKLM$ téglalap területéből levonjuk az $OK{B}_2$, $A_{2}N{B}_1$, $A_{1}M{B}_1$ derékszögű háromszögek és az $A_{2}NL{B}_2$ trapéz területét: $\begin{array}{c}{\displaystyle t=5\cdot 7-\frac{5\cdot 5}{2}-\frac{2\cdot 3}{2}-\frac{1\cdot 2}{2}-\frac{\left(2+3\right)\cdot 2}{2}=13\mathrm{,}5.}\end{array}$ Vagyis a kérdésben szereplő sokszög területe: $\begin{array}{c}{\displaystyle T=8t=8\cdot 13\mathrm{,}5=108.}\end{array}$ A tükrözések miatt a sokszög kerülete az $A_1{B}_1{A}_2{B}_2$ töröttvonal hosszának nyolcszorosa lesz: $\begin{array}{c}{\displaystyle K=8\cdot \left(A_1{B}_1+B_1{A}_2+A_2{B}_2\right)=8\cdot \left(\sqrt[]{5}+\sqrt[]{13}+\sqrt[]{5}\right)\approx 64\mathrm{,}6.}\end{array}$   4. Az $\mathrm{1,6,13,24,37,54,73,96,121,}\text{...}$ sorozat kettőnél nagyobb sorszámú tagjait úgy kaptuk, hogy a nála kettővel kisebb sorszámú taghoz hozzáadtuk a közbülső tag sorszámának hatszorosát. Már tudjuk, hogy a páros helyen álló számok a sorszám másodfokú függvényeként állíthatók elő. Mennyi a sorozat századik tagja?  (14 pont)   Megoldás. A feladat szövege alapján a sorozat $n$-edik tagja a következő módon kapható meg: $a_n=a_{n-2}+6\left(n-1\right)$. Mivel tudjuk, hogy a páros helyen álló számok a sorszám másodfokú függvényeként állíthatók elő, azért páros $n$ esetén a sorozat tagjait $a_n=a{n}^2+bn+c$ alakban keressük, ahol $a$, $b$ és $c$ valós együtthatók, de $a\ne 0$. Tudjuk, hogy $a_2=6$, $a_4=24$, $a_6=54$, ezért felírható a következő egyenletrendszer: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle 4a+2b+c}& {\displaystyle =\mathrm{6,}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle 16a+4b+c}& {\displaystyle =\mathrm{24,}}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle 36a+6b+c}& {\displaystyle =54.}\hfill & \text{(<mn>3</mn>)}\end{array}}$ Ha a nagyobb sorszámú egyenlet megfelelő oldalából kivonjuk az eggyel kisebb sorszámú egyenlet megfelelő oldalát (és osztunk 2-vel), akkor már csak két ismeretlen marad, két egyenlettel: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 6a+b}& {\displaystyle =\mathrm{9,}}\hfill \\ \hfill {\displaystyle 10a+b}& {\displaystyle =15.}\hfill \end{array}}$ Újabb kivonás, majd visszahelyettesítések után: $a=\frac{3}{2}$, $b=0$, $c=0$. Azaz $a_n=\frac{3}{2}{n}^2$. Ekkor $a_{100}=\frac{3}{2}\cdot {100}^2=15000$.   II. 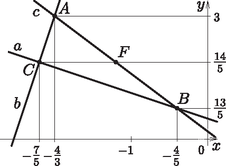rész     5. Adott három egyenes az egyenletével: $\begin{array}{c}{\displaystyle a:x+3y=\mathrm{7,}b:3x-y=-\mathrm{7,}c:3x+4y=8.}\end{array}$ $a)$ Mutassuk meg, hogy a három egyenes derékszögű háromszöget határoz meg. $b)$ Milyen messze van a derékszögű csúcs a szemközti oldal felezőpontjától? $c)$ Mekkora a háromszög beírt körének sugara?  (16 pont)   Megoldás. Az egyenesek egyenletének ismeretében tudjuk mindhárom egyenes normálvektorának koordinátáit: ${\text{n}}_a\left(1;3\right)$, ${\text{n}}_b\left(3;-1\right)$, ${\text{n}}_c\left(3;4\right)$. Mivel ${\text{n}}_a\cdot {\text{n}}_b=1\cdot 3+3\cdot \left(-1\right)=0$, azért ez a két normálvektor merőleges egymásra. Vagyis a rájuk merőleges $a$, illetve $b$ egyenesek is merőlegesek. Meg kell még vizsgálnunk, hogy a három egyenes valóban háromszöget határoz-e meg. A koordinátákból látható, hogy nincs olyan ${\lambda }_1$ valós szám, hogy ${\text{n}}_a={\lambda }_1\cdot {\text{n}}_c$, így ${\text{n}}_a\nparallel {\text{n}}_c$, azaz $a\nparallel c$. Hasonlóan az előzőhöz, nincs olyan ${\lambda }_2$ valós szám, hogy ${\text{n}}_b={\lambda }_2\cdot {\text{n}}_c$, így ${\text{n}}_b\nparallel {\text{n}}_c$, azaz $b\nparallel c$. Mivel az $x+3y=\mathrm{7,3}x-y=-7$ egyenletrendszernek $x=-\frac{7}{5}$, $y=\frac{14}{5}$   a megoldása, azért az $a$ és a $b$ egyenesek metszéspontja: $C(-\frac{7}{5};\frac{14}{5})$. Ha ezeket a koordinátákat behelyettesítjük a $c$ egyenes egyenletébe, akkor látható, hogy a $C$ pont nem illeszkedik a $c$ egyenesre, hiszen $3\cdot (-\frac{7}{5})+4\cdot \frac{14}{5}\ne 8$. Vagyis a három egyenes derékszögű háromszöget határoz meg. Megjegyzés. Az $a$ és a $b$ egyenesek merőlegessége csak szükséges, de nem elegendő feltétel. A fentiekben láthattunk egy gondolatmenetet arra, hogy a háromszög csúcsainak meghatározása nélkül is megmutatható a háromszög létezése. Természetesen a csúcsok koordinátáinak kiszámításával is belátható, hogy a háromszög létezik. $b)$ A $3x-y=-7$, $3x+4y=8$ egyenletrendszer megoldásával $(x=-\frac{4}{3}$, $y=3)$ kapjuk a háromszög egyik csúcsát: $A(-\frac{4}{3};3)$. Az $x+3y=7$, $3x+4y=8$ egyenletrendszer megoldásával $(x=-\frac{4}{5}$, $y=\frac{13}{5})$ kapjuk a háromszög másik csúcsát: $B(-\frac{4}{5};\frac{13}{5})$.     A $C$ csúcsnál található a derékszög, az $A$, illetve $B$ csúcsok koordinátáinak ismeretében pedig az $AB$ oldal $F\left(f_1;f_2\right)$ felezőpontjának koordinátái meghatározhatók: $\begin{array}{c}{\displaystyle f_1=\frac{-\frac{4}{3}-\frac{4}{5}}{2}=-\frac{16}{15}\mathrm{,}{f}_2=\frac{3+\frac{13}{5}}{2}=\frac{14}{5}\mathrm{.}}\end{array}$ A keresett szakasz hossza: $\begin{array}{c}{\displaystyle CF=\sqrt[]{{\left(-\frac{16}{15}+\frac{7}{5}\right)}^2+{\left(\frac{14}{5}-\frac{14}{5}\right)}^2}=\frac{1}{3}\mathrm{.}}\end{array}$ Megjegyzés. Készítettünk ábrát, de a koordináta-geometriának pontosan az az egyik ,,szépsége'', hogy ábra készítése nélkül is tökéletesen végigvihető a számolás. $c)$ A háromszög csúcsainak ismeretében: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle AC}& {\displaystyle =\sqrt[]{{\left(-\frac{7}{5}+\frac{4}{3}\right)}^2+{\left(\frac{14}{5}-3\right)}^2}=\frac{\sqrt[]{10}}{15}\mathrm{,}}\hfill \\ \hfill {\displaystyle BC}& {\displaystyle =\sqrt[]{{\left(-\frac{7}{5}+\frac{4}{5}\right)}^2+{\left(\frac{14}{5}-\frac{13}{5}\right)}^2}=\frac{\sqrt[]{10}}{5}\mathrm{,}}\hfill \\ \hfill {\displaystyle AB}& {\displaystyle =\sqrt[]{{\left(-\frac{4}{5}+\frac{4}{3}\right)}^2+{\left(\frac{13}{5}-3\right)}^2}=\frac{2}{3}\mathrm{.}}\hfill \end{array}}$ Az $ABC$ derékszögű háromszög területét felírhatjuk a két befogó hosszának ismeretében: $\begin{array}{c}{\displaystyle t_{ABC}=\frac{\frac{\sqrt[]{10}}{15}\cdot \frac{\sqrt[]{10}}{5}}{2}=\frac{1}{15}\mathrm{.}}\end{array}$ Az $ABC$ derékszögű háromszög kerületének fele az oldalak hosszának ismeretében: $\begin{array}{c}{\displaystyle s=\frac{k_{ABC}}{2}=\frac{\frac{\sqrt[]{10}}{15}+\frac{\sqrt[]{10}}{5}+\frac{2}{3}}{2}=\frac{2\sqrt[]{10}+5}{15}\mathrm{.}}\end{array}$ Az $ABC$ derékszögű háromszög területére felírhatjuk a következő összefüggés: $t_{ABC}=\varrho \cdot s$, ahol $\varrho$ a beírt kör sugarának a hossza. Az ismert mennyiségeket behelyettesítjük: $\begin{array}{c}{\displaystyle \frac{1}{15}=\varrho \cdot \frac{2\sqrt[]{10}+5}{15}\mathrm{,}\text{vagyis}\varrho =\frac{1}{2\sqrt[]{10}+5}\mathrm{.}}\end{array}$ A nevező gyöktelenítése után: $\varrho =\frac{2\sqrt[]{10}-5}{15}\left(\approx 0\mathrm{,}088\right)$.   6. Adott egy függvény a hozzárendelési utasításával: $\begin{array}{c}{\displaystyle f\left(x\right)=\frac{\frac{x+2}{x-2}-\frac{x-2}{x+2}}{\frac{x-2}{x+2}+1}\mathrm{.}}\end{array}$ $a)$ Adjuk meg azt a legbővebb halmazt, amely az $f\left(x\right)$ értelmezési tartománya lehet. $b)$ Adjuk meg $f\left(x\right)$ értékkészletét. $c)$ Hány rácspont illeszkedik $f\left(x\right)$ grafikonjára? Adjuk meg ezeket a pontokat. $\begin{array}{c}\end{array}$ (16 pont)   Megoldás. $a)$ A hozzárendelési utasításban a nevezők ne legyenek nullák. Vagyis $x\ne 2$, $x\ne -2$, illetve $\frac{x-2}{x+2}+1\ne 0$. Ez utóbbinak a bal oldalán közös nevezővel írjuk a két tagot: $\begin{array}{c}{\displaystyle \frac{x-2+x+2}{x+2}=\frac{2x}{x+2}\ne \mathrm{0,}\text{azaz}x\ne 0.}\end{array}$ Vagyis a legbővebb halmaz, ami az $f\left(x\right)$ függvény értelmezési tartománya lehet: $x\in \text{R}\backslash \left\{-2;0;2\right\}$. $b)$ Hozzuk egyszerűbb alakra a hozzárendelési utasításban szereplő kifejezést: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \left(\frac{x+2}{x-2}-\frac{x-2}{x+2}\right):\left(\frac{x-2}{x+2}+1\right)}& {\displaystyle =\frac{{\left(x+2\right)}^2-{\left(x-2\right)}^2}{\left(x-2\right)\left(x+2\right)}:\frac{x-2+x+2}{x+2}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{8x}{\left(x-2\right)\left(x+2\right)}\cdot \frac{x+2}{2x}=\frac{4}{x-2}\mathrm{.}}\hfill \end{array}}$ Tudjuk, hogy a $g\left(x\right)=\frac{4}{x-2}$ hozzárendeléssel adott függvény a $h\left(x\right)=\frac{1}{x}$ transzformációjával adódik, így azt is tudjuk, hogy az értékkészlete: $g\left(x\right)\in \text{R}\backslash \left\{0\right\}$. Az általunk vizsgált $f\left(x\right)$ függvény két hely kivételével azonos értékeket vesz fel, mint a $g\left(x\right)$. Mivel $g\left(-2\right)=-1$, $g\left(0\right)=-2$, és ezeken a helyeken az $f\left(x\right)$ nincs értelmezve, azért az $f\left(x\right)$ értékkészlete: $f\left(x\right)\in R\backslash \left\{-2;-1;0\right\}$. $c)$ A kérdést így is megfogalmazhatjuk: Hány darab olyan $x$ egész szám van az $f\left(x\right)$ értelmezési tartományában, amelyre a $\frac{4}{x-2}$ az $f\left(x\right)$ értékkészletében lévő egész szám lesz? A nevezőben szereplő $x-2$ a 4 osztója kell, hogy legyen. Ezek alapján az $x-2$ lehetséges értékei: $-4$; $-2$; $-1$; 1; 2; 4. Ekkor az $x$ értékei rendre: $-2$; 0; 1; 3; 4; 6. A $-2$ és a 0 nincs benne az értelmezési tartományban, ezért ezekkel az értékekkel nem kell tovább foglalkoznunk. A maradék négy számhoz a $\frac{4}{x-2}$ értékei rendre: $-4$; 4; 2; 1. Tehát négy darab rácspont illeszkedik $f\left(x\right)$ grafikonjára: $A\left(1;-4\right)$, $B\left(3;4\right)$, $C\left(4;2\right)$, $D\left(6;1\right)$.   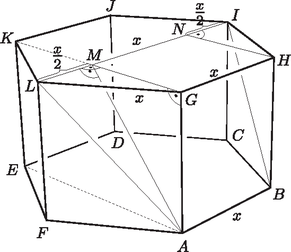7. A Pontos lépés nevű játéknak László szabályos hatszög alaplapú egyenes hasáb alakú dobozt tervez. A doboz alaplapja az $ABCDEF$, fedőlapja pedig a $GHIJKL$ szabályos hatszög. $a)$ Mekkora lenne az $ABHG$ oldallap területe, ha az $ABIL$ metszet területe $72\text{c<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}$-es? $b)$ Mekkora lenne az alaplap és az $ABIL$ sík hajlásszöge $AL=\sqrt[]{2}\cdot AB$ esetén? $\begin{array}{c}\end{array}$ (16 pont)   Megoldás. $a)$ Legyen $AB=x$, ekkor $LI=2x$, hiszen a szabályos hatszög oldaláról és a hosszabb átlójáról van szó. Tudjuk, hogy ezen két párhuzamos egyenes távolsága 8 cm, azaz $AM=8$. Az $LGM$ derékszögű   háromszögben $LM=\frac{x}{2}$, $LG=x$, ezért $MG=\frac{\sqrt[]{3}}{2}x$. Az $AMG$ derékszögű háromszögben az $AM$ és az $MG$ oldalhosszakat már kifejeztük, így $\begin{array}{c}{\displaystyle AG=\sqrt[]{8^2-{\left(\frac{\sqrt[]{3}}{2}x\right)}^2}=\sqrt[]{64-\frac{3}{4}{x}^2}\mathrm{.}}\end{array}$     Az $ABHG$ oldallap területe $x$ segítségével kifejezve: $\begin{array}{c}{\displaystyle t_{ABHG}=AB\cdot AG=x\cdot \sqrt[]{64-\frac{3}{4}{x}^2}\mathrm{.}}\end{array}$ Írjuk fel az $ABIL$ húrtrapéz területét is: $\begin{array}{c}{\displaystyle t_{ABIL}=\frac{\left(AB+IL\right)AM}{2}=\frac{\left(x+2x\right)\cdot 8}{2}=12x=72.}\end{array}$ Ebből kapjuk, hogy $x=6$. Tehát: $\begin{array}{c}{\displaystyle t_{ABHG}=6\cdot \sqrt[]{64-\frac{3}{4}{\cdot 6}^2}=6\cdot \sqrt[]{37}\approx 36\mathrm{,}5\text{(c<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>). }}\end{array}$ $b)$ Jelöljük most is a szabályos hatszögek oldalainak hosszát $x$-szel. A feladat feltétele szerint most $AL=\sqrt[]{2}\cdot x$. Vagyis az $AFL$ derékszögű háromszög egyenlőszárú: $FL=x$, azaz a két párhuzamos alaplap távolsága $x$. A szabályos hatszögben $MG=\frac{\sqrt[]{3}}{2}x$ adódik ebben az esetben is. A szabályos hatszög és az egyenes hasáb tulajdonságait felhasználva kapjuk, hogy a keresett szög az $EAM$ szög, amivel azonos nagyságú az $AMG$ szög, hiszen váltószögek. Az $AMG$ derékszögű háromszögben felírhatjuk ennek a szögnek a tangensét: $\begin{array}{c}{\displaystyle \frac{x}{\frac{\sqrt[]{3}}{2}x}=\frac{2\sqrt[]{3}}{3}\mathrm{.}}\end{array}$ A keresett hajlásszög kb. $49\mathrm{,}{1}^{\circ }$.   8. 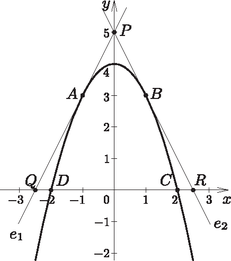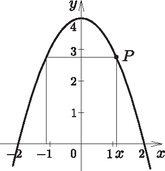$a)$ Az $f\left(x\right)=4-x^2$ hozzárendeléssel adott függvény grafikonjához az $1$ és a $-1$ abszcisszájú pontjában húzott érintők, valamint az $x$ tengely meghatároz egy háromszöget. A háromszöget a függvény görbéje mentén szétvágjuk. Mekkora a függvény görbéje mellett jobbra, balra és fönt keletkezett síkidomok területének összege? $b)$ Egy alagút keresztmetszetét jó közelítéssel az $f\left(x\right)=4-x^2$ hozzárendelésű függvény grafikonja és az $x$ tengely adja. A koordinátarendszer egysége $1$ méternek felel meg. Mekkora a maximális térfogata annak a $6$ méter hosszú téglatestnek, amit egyik lapján csúsztatva át lehet tolni az alagúton?  (16 pont)   Megoldás. $a)$ Mivel $f\left(-1\right)=4-{\left(-1\right)}^2=3$, $f\left(1\right)=4-1^2=3$, azért az $A\left(-1;3\right)$, és a $B\left(1;3\right)$ pontokra illeszkedő érintőkről van szó. Az érintő meredekségét az első derivált adja: $f\text{'}\left(x\right)=-2x$. Mivel $f\text{'}\left(-1\right)=-2\cdot \left(-1\right)=2$, azért az $A$ pontra illeszkedő $e_1$ érintő egyenlete: $y-3=2\left(x+1\right)$. Mivel $f\text{'}\left(1\right)=-2\cdot 1=-2$, azért a $B$ pontra illeszkedő $e_2$ érintő egyenlete: $y-3=-2\left(x-1\right)$. Az érintők egyenleteiből álló egyenletrendszer megoldása adja a két egyenes metszéspontjának koordinátáit: $P\left(0;5\right)$.     Az $e_1$ érintő a $Q(-\frac{5}{2};0)$, az $e_2$ érintő az $R(\frac{5}{2};0)$ pontban metszi az $x$ tengelyt. Ezek alapján a $PQR$ egyenlőszárú háromszög területe: $\begin{array}{c}{\displaystyle t_{PQR}=\frac{QR\cdot OP}{2}=\frac{5\cdot 5}{2}=\frac{25}{2}\mathrm{.}}\end{array}$ Az $f\left(x\right)$ grafikonja a $C\left(2;0\right)$ és a $D\left(-2;0\right)$ pontokban metszi az $x$ tengelyt. Ezért a függvény görbealatti területét a következő integrál adja: $\begin{array}{c}{\displaystyle t_1=\underset{-2}{\overset{2}{\int }}\left(4-x^2\right)dx={\left[4x-\frac{x^3}{3}\right]}_{-2}^2=8-\frac{8}{3}+8-\frac{8}{3}=\frac{32}{3}\mathrm{.}}\end{array}$ A kérdezett síkidomok területének összegét a $PQR$ háromszög területének és a $t_1$ területnek a különbsége adja: $\begin{array}{c}{\displaystyle t=\frac{25}{2}-\frac{32}{3}=\frac{11}{6}\mathrm{.}}\end{array}$ $b)$ Az adatok alapján megállapítható, hogy a téglatest 6 méteres élét vízszintes helyzetben kell csúsztatni. Vagyis a rá merőleges téglalap területének kell maximálisnak lenni. Készítsünk vázlatrajzot és használjuk a jelöléseit. A kérdéses téglalap területe: $\begin{array}{c}{\displaystyle t\left(x\right)=2x\left(4-x^2\right)=8x-2x^3\mathrm{.}}\end{array}$ Ennek a függvénynek keressük a maximumhelyét a $\left]0;2\right]$ intervallumon. Vizsgáljuk az első deriváltjának a zérushelyeit: $\begin{array}{c}{\displaystyle f\text{'}\left(x\right)=8-6x^2=0.}\end{array}$     Az adott intervallumon: $\begin{array}{c}{\displaystyle x=\frac{2}{\sqrt[]{3}}=\frac{2\sqrt[]{3}}{3}\mathrm{.}}\end{array}$ Ezen a helyen a derivált előjelet vált (pozitívról negatívra), vagyis valóban a függvénynek ezen a helyen maximuma van. Ezek alapján a maximális térfogatú téglatest éleinek hossza: $2x=\frac{4\sqrt[]{3}}{3}$, $4-x^2=\frac{8}{3}$, 6. Tehát a térfogata: $\begin{array}{c}{\displaystyle V=\frac{4\sqrt[]{3}}{3}\cdot \frac{8}{3}\cdot 6=\frac{192\sqrt[]{3}}{9}\approx 36\mathrm{,}95\text{(<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>). 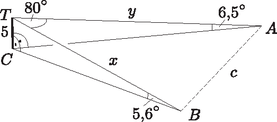}}\end{array}$   9. Sík talajon az $5$ méter magas, függőlegesen álló oszlop teteje a sík $A$ pontjából $6\mathrm{,}{5}^{\circ }$, a $B$ pontjából pedig $5\mathrm{,}{6}^{\circ }$ emelkedési szögben látszik. Az oszlop tetejéről az $AB$ távolság ${80}^{\circ }$-os látószög alatt látható. $a)$ Írjuk le röviden, hogy hogyan határoznánk meg az $ABC$ háromszög területét ($C$ az oszlop alja), ha az $AB$ hosszát ismernénk. $b)$ Mekkora az $AB$ távolság?  (16 pont)   Megoldás. $a)$ Készítsünk ábrát és használjuk az ábra jelöléseit.     Az $ACT$ derékszögű háromszögben a $CT$ hosszának, és az $A$ csúcsnál lévő szög nagyságának ismeretében, tangens használatával az $AC$ hossza meghatározható. A $BCT$ derékszögű háromszögben a $CT$ hosszának, és a $B$ csúcsnál lévő szög nagyságának ismeretében, tangens használatával az $BC$ hossza meghatározható. Mivel a szöveg szerint $AB$ hosszát ismerjük, azért az $ABC$ háromszögben minden oldal hossza így ismert lett. Felírhatjuk a koszinusztételt például a $C$ csúcsnál található szög felhasználásával. Így ez a $\gamma$ szög is ismert lesz. Ezek után: $\begin{array}{c}{\displaystyle t_{ABC}=\frac{CA\cdot CB\cdot \text{sin}\gamma }{2}\mathrm{.}}\end{array}$ Megjegyzés. A három oldal hosszának ismeretében a Heron-féle képletet is használhatjuk a háromszög területének meghatározására. $b)$ Az $ACT$ derékszögű háromszögben: $\text{sin}6\mathrm{,}{5}^{\circ }=\frac{5}{y}$, azaz   $y=\frac{5}{\text{sin}6\mathrm{,}{5}^{\circ }}$. A $BCT$ derékszögű háromszögben: $\text{sin}5\mathrm{,}{6}^{\circ }=\frac{5}{x}$, azaz $x=\frac{5}{\text{sin}5\mathrm{,}{6}^{\circ }}$. Írjuk fel az $ABT$ háromszögre a koszinusztételt: $\begin{array}{c}{\displaystyle c^2={\left(\frac{5}{\text{sin}6\mathrm{,}{5}^{\circ }}\right)}^2+{\left(\frac{5}{\text{sin}5\mathrm{,}{6}^{\circ }}\right)}^2-2\cdot \frac{5}{\text{sin}6\mathrm{,}{5}^{\circ }}\cdot \frac{5}{\text{sin}5\mathrm{,}{6}^{\circ }}\cdot \text{cos}{80}^{\circ }\mathrm{,}c\approx 61\mathrm{,}6.}\end{array}$ Vagyis az $AB$ távolság kb. 61,6 méter.