Cím:	Megoldásvázlatok a 2013/7. sz. emelt szintű gyakorló feladataihoz
Szerző(k):	Nemecskóné Szabó Zsuzsanna
Füzet:	2013/november, 462 - 467. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Péter a telefonján az egyik hónapban $18$ hívást kezdeményezett és $60$ percet beszélt hálózaton belül. Hálózaton kívül pedig $11$ hívást kezdeményezett és $45$ percet beszélt. 10 db SMS-t küldött. Hasonlítsuk össze, és számításokkal igazoljuk, hogy a megadott tarifacsomagok közül (,,Haver 1'', ,,Haver 2'') melyik lett volna kedvezőbb számára az adott hónapban.   ${\displaystyle \begin{array}{|ccc|}\hline {\displaystyle \text{Tarifacsomag neve}}\hfill & \hfill {\displaystyle \text{Haver1}}\hfill & \hfill {\displaystyle \text{Haver2}}\hfill \\ {\displaystyle }\hfill & \hfill {\displaystyle \text{1710 Ft}}\hfill & \hfill {\displaystyle \text{3850 Ft}}\hfill \\ {\displaystyle \text{Lebeszélhető havidíj}}\hfill & \hfill {\displaystyle \text{100\%-ban hálózaton belül}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>60</mn><mo>\%</mo></math>-ban hálózaton belül}}\hfill \\ {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>40</mn><mo>\%</mo></math>-ban hálózaton kívül}}\hfill \\ {\displaystyle \text{Percdíj a havidíj }}\hfill & \hfill {\displaystyle \text{38 Ft}}\hfill & \hfill {\displaystyle \text{35 Ft}}\hfill \\ {\displaystyle \text{felhasználásáig }}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill \\ {\displaystyle \text{Percdíj a havidíj }}\hfill & \hfill {\displaystyle \text{40 Ft}}\hfill & \hfill {\displaystyle \text{38 Ft}}\hfill \\ {\displaystyle \text{felhasználása után}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill \\ {\displaystyle \text{SMS küldés díja}}\hfill & \hfill {\displaystyle \text{40 Ft}}\hfill & \hfill {\displaystyle \text{38 Ft}}\hfill \\ {\displaystyle \text{Kapcsolási díj}}\hfill & \hfill {\displaystyle \text{3 Ft}}\hfill & \hfill {\displaystyle \text{3 Ft}}\hfill \\ \hline\end{array}}$   A kapcsolási díj a havidíj-lebeszélhetőségbe nem számít bele, mindig a havidíjon felül kerül kiszámlázásra.  (11 pont)   Megoldás. A ,,Haver 1'' tarifacsomag esetén $1710:38=45$ perc beszélhető le hálózaton belül. Marad neki $60-45=15$ perc. Ezért a havidíjon felül fizetendő: $15\cdot 40=600$ Ft. A hálózaton kívüli percekért fizetendő $45\cdot 40=1800$ Ft, az SMS-ért $10\cdot 40=400$ Ft. Kapcsolási díj: $\left(18+11\right)\cdot 3=87$ Ft. A költség összesen: $\begin{array}{c}{\displaystyle 1710+600+1800+400+87=4597\text{Ft. }}\end{array}$ A ,,Haver 2'' tarifacsomag esetén mivel $3850\cdot 0\mathrm{,}6=2310$ és $2310:35=66$, azért 66 percet beszélhetne hálózaton belül. Ebből csak 60 percet beszélt le, ami $2310$ Ft. Mivel $3850\cdot 0\mathrm{,}4=1540$ és $1540:35=44$, azért 44 percet beszélhet hálózaton kívül, de ő beszélt még 1 percet: $1540+38=1578$ Ft. Az SMS-ért $10\cdot 38=380$ Ft-ot, a kapcsolási díjért $29\cdot 3=87$ Ft-ot fizetett. Összes költség: $\begin{array}{c}{\displaystyle 2310+1578+380+87=4355\text{Ft. }}\end{array}$ Tehát a ,,Haver 2'' kedvezőbb a számára, $4597-4355=242$ Ft-tal.   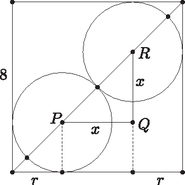2. Egy négyzet alapú hasáb alakú doboz alapéle 8 cm. A doboz négyzet alakú aljába éppen belefér két egyforma átmérőjű, körlapjával az alaplapon fekvő érem úgy, hogy az érmék a doboz 2-2 szomszédos oldallapját és egymást is érintik. Mekkora az érmék átmérője?  (12 pont)   Megoldás. Használjuk az ábra jelöléseit. Legyen $PR=2r=d$; $PQ=QR=x$. A $PQR$ egyenlő szárú derékszögű háromszögben a Pitagorasz-tétel szerint: $\begin{array}{c}{\displaystyle {\left(2r\right)}^2=x^2+x^2\mathrm{,}\text{ebből}x=\sqrt[]{2}\cdot r\mathrm{.}}\end{array}$     Mivel a négyzet oldala 8 cm, azért $2r+x=8$, azaz $2r+\sqrt[]{2}r=8$. Vagyis $r=\frac{8}{2+\sqrt[]{2}}$. Tehát az érmék átmérője: $d=2r\approx 4\mathrm{,}7$ cm.   3. Oldjuk meg a következő egyenleteket a valós számok halmazán: $a)$ $\text{cos}2x+5\cdot \text{sin}x+2=0$;  (7 pont) $b)$ $2\text{log}{}_{5}x-\frac{3}{\text{log}{}_{5}x}=5$.  (7 pont)   Megoldás. $a)$ Felhasználva, hogy $\text{cos}2x=\text{cos}{}^{2}x-\text{sin}{}^{2}x$ és $\text{cos}{}^{2}x=1-\text{sin}{}^{2}x$, az egyenlet a következő másodfokú egyenletre vezet: $\begin{array}{c}{\displaystyle 2\cdot \text{sin}{}^{2}x-5\cdot \text{sin}x-3=0.}\end{array}$ Ennek gyökei: $\text{sin}x=-\frac{1}{2}$ és $\text{sin}x=3$. Ez utóbbiból a szinusz függvény értékkészlete miatt nem adódik megoldás. Az egyenlet megoldása: $\begin{array}{c}{\displaystyle x_1=-\frac{\pi }{6}+k\cdot 2\pi \mathrm{,}{x}_2=\frac{7\pi }{6}+l\cdot 2\pi \mathrm{,}\text{ahol}k\mathrm{,}l\in \text{Z}\mathrm{.}}\end{array}$ Ezek valóban megoldásai ez eredeti egyenletnek. $b)$ Az egyenlet mindkét oldalát $\text{log}{}_{5}x$-szel megszorozva és rendezve, az előzőhöz hasonló másodfokú egyenlethez jutunk: $\begin{array}{c}{\displaystyle 2\text{log}{}_5^{2}x-5\text{log}{}_{5}x-3=0.}\end{array}$ Ebből ${\displaystyle \begin{array}{cccccccccccc}\hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle }\hfill & \hfill {\displaystyle }& {\displaystyle \text{log}{}_5{x}_1}\hfill & {\displaystyle =-\frac{1}{2}\mathrm{,}}\hfill & \hfill {\displaystyle \text{amiből}{x}_1}& {\displaystyle =\frac{1}{\sqrt[]{5}}=\frac{\sqrt[]{5}}{5};}\hfill & {\displaystyle }\hfill & \hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle }\hfill \\ \hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle }\hfill & \hfill {\displaystyle }& {\displaystyle \text{log}{}_5{x}_2}\hfill & {\displaystyle =\mathrm{3,}}\hfill & \hfill {\displaystyle \text{amiből}{x}_2}& {\displaystyle =125.}\hfill & {\displaystyle }\hfill & \hfill {\displaystyle }& {\displaystyle }\hfill \end{array}}$ Ezek a megoldások kielégítik az eredeti egyenletet.   4. Egy $10$ pontos tesztfeladatot harminc tanuló oldott meg. Az eredmény a következő lett:   ${\displaystyle \begin{array}{ccccccccc}\hfill {\displaystyle \text{ pontszám}}\hfill & \hfill {\displaystyle \text{3}}\hfill & \hfill {\displaystyle \text{4}}\hfill & \hfill {\displaystyle \text{5}}\hfill & \hfill {\displaystyle \text{6}}\hfill & \hfill {\displaystyle \text{7}}\hfill & \hfill {\displaystyle \text{8}}\hfill & \hfill {\displaystyle \text{9}}\hfill & \hfill {\displaystyle \text{10}}\hfill \\ \hfill {\displaystyle \text{gyakoriság}}\hfill & \hfill {\displaystyle \text{2}}\hfill & \hfill {\displaystyle \text{3}}\hfill & \hfill {\displaystyle \text{7}}\hfill & \hfill {\displaystyle \text{2}}\hfill & \hfill {\displaystyle \text{2}}\hfill & \hfill {\displaystyle \text{5}}\hfill & \hfill {\displaystyle \text{5}}\hfill & \hfill {\displaystyle \text{4}}\hfill \end{array}}$     $a)$ A tanár gratulált az osztálynak, mert az egyik középértéknél a tanulók $\frac{3}{5}$ része több pontot ért el. Melyik középértékre gondolt a tanár?  (6 pont) $b)$ Két tanuló később írta meg a tesztet. Az ő eredményüket is beleszámítva a medián 0,5-del; az átlag 0,075-del nőtt. Hány pontot érhettek el ők?  (8 pont)   Megoldás. $a)$ A pontszámok átlaga: $\begin{array}{c}{\displaystyle \left(3\cdot 2+4\cdot 3+5\cdot 7+6\cdot 2+7\cdot 2+8\cdot 5+9\cdot 5+10\cdot 4\right):30=204:30=6\mathrm{,}8.}\end{array}$ Ennél jobbat írt 16 fő. Mivel $\frac{16}{30}<\frac{3}{5}$, azért nem az átlagra gondolt. A medián, azaz a 15. és 16. elem átlaga: $\frac{7+7}{2}=7$. Ennél jobbat írt 14 fő.   Mivel $\frac{14}{30}<\frac{3}{5}$, azért nem a mediánra gondolt. A módusz, azaz a leggyakrabban előforduló elem: 5.   Ennél jobbat írt 18 fő. Mivel $\frac{18}{30}=\frac{3}{5}$, azért a tanár a móduszra gondolt.   $b)$ A két tanuló pontszámát jelölje $x$ és $y$. Az új átlag: $\frac{204+x+y}{32}=6\mathrm{,}875$, ebből $x+y=16$. A szóba jöhető felbontások: $16=6+10=7+9=8+8$. Ezek közül csak az $x=y=8$ jöhet szóba, mert ekkor a medián 0,5-del nő; a másik két esetben a medián nem változik. Tehát a tesztet később megíró mindkét tanuló pontszáma 8. Ez a megoldás valóban eleget tesz mindkét feltételnek.   II. rész     5. A ,,Vigyáz(z)6'' című játékban $1$-től $104$-ig számozott kártyák szerepelnek. A lapokon ökörfejek is találhatók a következő szabályok szerint: ‐ az $55$-ös lapon 7 db; ‐ a többi $5$-re végződő számot tartalmazó lapon 2-2 db; ‐ a többi azonos számjegyekből álló kétjegyű számot tartalmazó lapon 5-5 db; ‐ a $0$-ra végződő számot tartalmazó lapokon 3-3 db; ‐ az összes többi lapon 1-1 db ökörfej található. A játék elején $4$ lapot felcsapnak, minden játékos 10-10 lapot kap, a többi lap pedig talonba kerül. $a)$ Hány ökörfej található a lapokon összesen?  (4 pont) $b)$ Mennyi annak a valószínűsége, hogy a négy felcsapott lap mindegyikén egynél több ökörfej szerepel?  (6 pont) $c)$ Hat játékos esetén mi a valószínűsége, hogy a talonban van legalább egy olyan lap, amelyen $5$ vagy annál több ökörfej szerepel?  (6 pont)   Megoldás. $a)$ A megadott intervallumon hét ökörfejet tartalmazó kártya: 55 (1 lap); két ökörfejet tartalmazó kártyák: 5, 15, 25, 35, 45, 65, 75, 85, 95 (9 lap); öt ökörfejet tartalmazó kártyák: 11, 22, 33, 44, 66, 77, 88, 99 (8 lap); három ökörfejet tartalmazó kártyák: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 (10 lap). Ez összesen 28 lap. A többi 76 lapon csak egy ökörfej található. Vagyis az ökörfejek száma összesen: $\begin{array}{c}{\displaystyle 1\cdot 7+9\cdot 2+8\cdot 5+10\cdot 3+76\cdot 1=171\text{db. }}\end{array}$   $b)$ A klasszikus valószínűségi mező esetén alkalmazható képlettel dolgozunk.   Kedvező esetek száma $=\left(\genfrac{}{}{0ex}{}{28}{4}\right)$, az összes esetek száma $=\left(\genfrac{}{}{0ex}{}{104}{4}\right)$, vagyis $\begin{array}{c}{\displaystyle p=\frac{\left(\genfrac{}{}{0ex}{}{28}{4}\right)}{\left(\genfrac{}{}{0ex}{}{104}{4}\right)}\approx 0\mathrm{,}00445}\end{array}$ a valószínűsége annak, hogy a négy felcsapott lap mindegyikén egynél több ökörfej van.   $c)$ 5 vagy annál több (7) ökörfej $8+1=9$ db lapon szerepel; $104-9=95$ db lapon ennél kevesebb ökörfej van. Hat játékos esetén 40 db lap van a talonban. Érdemes először a komplementer esemény valószínűségét meghatározni. Az eredeti eseményt $A$-val jelölve, $\overline{A}=\{$a talonban levő lapok között nincs olyan, amelyen 5 vagy annál több ökörfej szerepel$\}$. Ebben az esetben is klasszikus valószínűségi mezőről van szó, $\begin{array}{c}{\displaystyle p\left(\overline{A}\right)=\frac{\left(\genfrac{}{}{0ex}{}{95}{40}\right)}{\left(\genfrac{}{}{0ex}{}{104}{40}\right)}\approx 0\mathrm{,}01.}\end{array}$ Tehát $p\left(A\right)=1-p\left(\overline{A}\right)\approx 0\mathrm{,}99$ a valószínűsége annak, hogy hat játékos esetén van legalább egy olyan lap a talonban, amelyen 5 vagy annál több ökörfej szerepel.     6. Egy üzemben henger alakú, egyliteres mérőedényeket gyártanak. Mekkora legyen a henger alapkörének sugara, illetve a henger magassága, hogy az anyagfelhasználás minimális legyen $a)$ fedetlen;  (8 pont) $b)$ fedett mérőedény esetén?  (8 pont) A választ milliméter pontossággal adjuk meg.   Megoldás. $a)$ A henger magassága legyen $m$; alapkörének sugara legyen $r$. A henger térfogata: $V=r^2\pi \cdot m=1\text{d<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>}$, ezért $m=\frac{1}{r^2\pi }$ dm. Az anyagfelhasználás akkor minimális, ha a henger felszíne minimális. $a)$ Fedetlen edény esetén a felszín: $A=r^2\pi +2r\pi m$, $A\left(r\right)=r^2\pi +\frac{2}{r}$. Ennek a kifejezésnek akkor van minimuma, ha az első deriváltja 0 és a második deriváltja pozitív: $\begin{array}{c}{\displaystyle A\text{'}\left(r\right)=2r\pi -\frac{2}{r^2}=0\text{és}A\text{'}\text{'}\left(r\right)=2\pi +\frac{4}{r^3}>0.}\end{array}$ Az elsőből $\begin{array}{c}{\displaystyle r=\sqrt[3]{\frac{1}{\pi }}\mathrm{,}m=\frac{1}{\sqrt[3]{\frac{1}{{\pi }^2}}\cdot \pi }=\sqrt[3]{\frac{1}{\pi }}\approx 0\mathrm{,}68\text{dm. }}\end{array}$ Ekkor $A\text{'}\text{'}\left(\sqrt[3]{\frac{1}{\pi }}\right)>0$. Vagyis az anyagfelhasználás akkor minimális, ha $r=m\approx 0\mathrm{,}68\text{dm = 68}$ mm. $b)$ Fedett edény esetén a felszín: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle A\left(r\right)}& {\displaystyle =2r^2\pi +2r\pi m=2r^2\pi +\frac{2}{r}\mathrm{,}}\hfill \\ \hfill {\displaystyle A\text{'}\left(r\right)}& {\displaystyle =4r\pi -\frac{2}{r^2}=0\text{és}A\text{'}\text{'}=4\pi +\frac{4}{r^3}>0.}\hfill \end{array}}$ Az elsőből $r=\sqrt[3]{\frac{1}{2\pi }}\approx 0\mathrm{,}54$ dm és $m=\sqrt[3]{\frac{4}{\pi }}\approx 1\mathrm{,}08$ dm, ekkor $A\text{'}\text{'}\left(\sqrt[3]{\frac{4}{\pi }}\right)>0$. Vagyis az anyagfelhasználás akkor minimális, ha $r\approx 0\mathrm{,}54\text{dm=54}$ mm; $m\approx 1\mathrm{,}08\text{dm=108}$ mm.   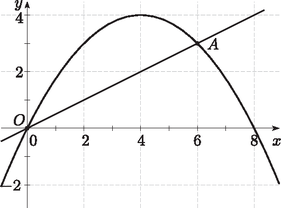7. Az $y=a{x}^2+bx+c$ egyenletű parabola áthalad a $\left(8;0\right)$ ponton és az origón. Az origóba húzott érintőjének iránytangense $2$. $a)$ Határozzuk meg $a$, $b$ és $c$ értékét.  (6 pont) $b)$ Az origón és a parabola $6$ abszcisszájú pontján keresztül szelőt húzunk. Mekkora területet zár közre ez a szelő és a parabola?  (10 pont)   Megoldás. $a)$ Mivel a parabola áthalad a $\left(8;0\right)$ és a $\left(0;0\right)$ pontokon, felírhatjuk a következő egyenleteket: $0=a\cdot 64+b\cdot 8+c$, $0=a\cdot 0+b\cdot 0+c$. Ezekből kapjuk, hogy $c=0$ és $a=-\frac{1}{8}b$.     Az origóba húzott érintő iránytangense a pontbeli első derivált:   $\begin{array}{c}{\displaystyle f\text{'}\left(x\right)=2ax+b\mathrm{,}f\text{'}\left(0\right)=0+b=2.}\end{array}$ Tehát $a=-\frac{1}{4}$; $b=2$; $c=0$. $b)$ Mivel $f\left(x\right)=-\frac{1}{4}{x}^2+2x$, azért $f\left(6\right)=3$. Az origón és az $A\left(6;3\right)$ pontokon áthaladó szelő egyenlete: $y=\frac{1}{2}x$. A kérdéses terület: $\begin{array}{c}{\displaystyle \underset{0}{\overset{6}{\int }}\left(-\frac{1}{4}{x}^2+2x-\frac{1}{2}x\right)dx=\underset{0}{\overset{6}{\int }}\left(-\frac{1}{4}{x}^2+\frac{3}{2}x\right)dx={\left[-\frac{1}{4}\cdot \frac{x^3}{3}+\frac{3}{2}\cdot \frac{x^2}{2}\right]}_0^6=9.}\end{array}$   A parabola és a szelő által közrezárt terület 9 területegység.   8. $a)$ Bizonyítsuk be, hogy minden n természetes számra $64\mid 9^n-8n-1$.  (8 pont) $b)$ Igaz-e, hogy ${2013}^2+2014\mid {2013}^{2014}-2013$? Indokoljuk válaszunkat.  (8 pont)   Megoldás. $a)$ Teljes indukcióval bizonyítunk. $n=0$-ra: $64\mid 0$; igaz; ($n=1$-re: $64\mid 0$; igaz; $n=2$-re: $64\mid 64$; igaz). Tegyük fel, hogy $n=k$-ra igaz, vagyis $64\mid 9^k-8k-1$. Be kell látnunk, hogy $n=k+1$-re is igaz, azaz $64\mid 9^{k+1}-8\left(k+1\right)-1$. A kifejezést átalakíthatjuk a következő módon: $\begin{array}{c}{\displaystyle 9\cdot 9^k-8k-9=9\cdot \left(9^k-8k-1\right)+64k\mathrm{.}}\end{array}$ Az utóbbi kifejezés első tagja az indukciós feltevés miatt, a második tag nyilvánvalóan osztható 64-gyel, tehát az összeg is osztható 64-gyel. Ezzel az állítást igazoltuk. $b)$ Legyen $a=2013$. Ekkor a baloldal így írható: $a^2+a+1$. A jobboldal: $\begin{array}{c}{\displaystyle a^{2014}-a=a\left(a^{2013}-1\right)=a[{\left(a^3\right)}^{671}-1^{671}]=a\left(a^3-1\right)\left(a^{670}+a^{669}+\text{...}+a+1\right)\mathrm{.}}\end{array}$ Mivel $a^3-1=\left(a-1\right)\left(a^2+a+1\right)$, azért az állítás igaz.   9. Egy turisták pihenőjeként szolgáló építmény legfelső csúcsában három darab szabályos ötszög találkozik az ábrán látható módon.     A szabályos ötszögek oldalai 1,5 m hosszúak. Az építmény oldallapjai téglalapok, amelyeknek a talajra merőleges oldalai szintén 1,5 m hosszúak. $a)$ Milyen magas az építmény?  (8 pont) $b)$ Mekkora az építmény alapterülete?  (8 pont)   Megoldás. $a)$ Használjuk az 1. ábra jelöléseit. A szöveg alapján $a=1\mathrm{,}5$ m. Az ábrán $AD=BG$, mert a tetőszerkezetet tekinthetjük egy szabályos dodekaéder részének, amelyhez a $C$ csúcsnál egy újabb szabályos ötszög csatlakozna. Legyen $AD=BG=b$; $FO=x$; $FD=y$; $OD=m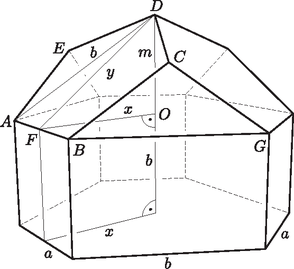$.   1. ábra   Az ábrán $b$-vel jelölt szakaszok hossza megegyezik a szabályos ötszög átlójával. A szabályos ötszög egy szöge: $\begin{array}{c}{\displaystyle \alpha =\frac{3\cdot 180}{5}={108}^{\circ }\mathrm{.}}\end{array}$ Ugyanekkora a $BCG\sphericalangle$ nagysága is. A $BGC$ háromszögben a koszinusz-tétel alapján: $b^2=2a^2-2a^2\cdot \text{cos}{108}^{\circ }$, ebből $b\approx 2\mathrm{,}43$ m. Az $EAD$ háromszögben $\begin{array}{c}{\displaystyle EAD\sphericalangle =EDA\sphericalangle =\frac{{180}^{\circ }-{108}^{\circ }}{2}={36}^{\circ }\mathrm{.}}\end{array}$ Az $AFD$ háromszögben $DAF\sphericalangle ={108}^{\circ }-EAD\sphericalangle ={72}^{\circ }$, az 1. ábrán $y$-nal jelölt szakaszra felírható az $AFD$ háromszögben: $\text{sin}{72}^{\circ }=\frac{y}{b}$. Ebből $y\approx 2\mathrm{,}31$ m. Az 1. ábrán $x$-szel jelölt szakasz kiszámításához tekintsük az alaplapot alkotó hatszöget. Ennek szemközti oldalai párhuzamosak és oldalainak hossza rendre: $a$, $b$, $a$, $b$, $a$, $b$, mert a megfelelő oldalak ${120}^{\circ }$-os elforgatottjai egymásnak az $OD$ egyenes, mint térbeli forgástengely körül (ez a forgatás a szerkezetet és a dodekaédert is önmagába viszi). Ezért ez a hatszög kiegészíthető szabályos háromszöggé a 2. ábrán látható módon. 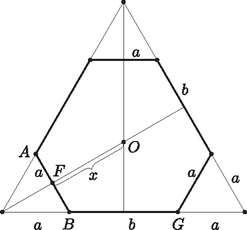  2. ábra   Az ábra alapján az $x$-szel jelölt szakasz kiszámítható a $b+2a$ oldalú szabályos háromszög súlyvonala kétharmad részének és az $a$ oldalú szabályos háromszög magasságának különbségeként: $\begin{array}{c}{\displaystyle x=\frac{2}{3}\cdot \frac{\sqrt[]{3}}{2}\left(b+2a\right)-\frac{\sqrt[]{3}}{2}a\approx 1\mathrm{,}84\text{m. }}\end{array}$ A $DFO$ háromszögben a Pitagorasz-tételt felírva: $m=\sqrt[]{y^2-x^2}\approx 1\mathrm{,}40$ m. Az építmény magassága $M=a+m\approx 2\mathrm{,}9$ m. $b)$ Az alapterületet kiszámolhatjuk úgy, hogy a $b+2a$ oldalú szabályos háromszög területéből kivonjuk az $a$ oldalú szabályos háromszög területének háromszorosát: $\begin{array}{c}{\displaystyle T=\frac{\sqrt[]{3}}{4}\cdot {\left(b+2a\right)}^2-3\cdot \frac{\sqrt[]{3}}{4}\cdot a^2\approx 9\mathrm{,}84\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>. }}\end{array}$ Tehát az építmény alapterülete: 9,84 m${}^2$.