Cím:	A 2012‐2013. évi Arany Dániel Matematikai Tanulóverseny feladatai
Füzet:	2013/november, 450 - 455. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   A 2012‐2013. évi Arany Dániel Matematikai Tanulóverseny feladatai KEZDŐK       I. kategória: Legfeljebb heti 3 órában matematikát tanuló középiskolai tanulók       Első (iskolai) forduló       1. Az $a$ és $b$ nullától különböző valós számokra teljesül az alábbi összefüggés: $\begin{array}{c}{\displaystyle a^3+\left(3a^2+1\right)b+\left(3b^2+1\right)a+b^3=0.}\end{array}$ Mennyi lehet az $\frac{a}{b}$ hányados értéke?     2. A 2011, 2012, 2013, 2014 számok közül melyek írhatók fel kettő vagy több egymást követő pozitív páratlan szám összegeként?     3. Egy esküvői vacsorán egy hatfős asztaltársaság tagjai közül néhányan ismerik egymást. A násznagy megkérdezi az asztaltársaság tagjait, hogy hány személyt ismernek az asztalnál ülők közül. Az első öt válaszadó által kimondott öt szám mindegyike különbözik egymástól. Hány embert ismerhet a hatodik személy az asztalnál ülők közül? (Az ismeretségeket kölcsönösnek tételezzük fel.)     4. Hány olyan különböző (egymással nem egybevágó) háromszög van, amelynek két oldala 2 cm és 7 cm hosszúságú, és a harmadik oldalhoz tartozó súlyvonal cm-ben vett mérőszáma is egész szám?     Második forduló       1. Egy osztályban minden diák jár a háromféle szakkör valamelyikére: 17-en matematikára, 13-an fizikára és 11-en kémiára. Azok száma, akik pontosan kétféle szakkörre járnak éppen négyszerese azok számának, akik mindhárom szakkörön részt vesznek. Hányan járnak mindhárom szakkörre és mennyi az osztálylétszám, ha az osztályba járó fiúk egyharmad része szemüveges, valamint a nem szemüveges fiúk száma egyenlő a lányok számával?     2. Van 6-6 piros és zöld matricánk, melyeken az 1, 2, 3, 4, 5, 6 számok találhatók mindkét szín esetében. Felragasztottuk valahogyan a piros matricákat egy kocka 6 oldalára. Ezt követően a zöld matricákat is felragasztjuk egy-egy oldalra. Ezután a kocka minden egyes csúcsára ráírjuk, hogy mennyi a csúcsot tartalmazó kockalapokon lévő 3 piros és 3 zöld szám összege. A zöld matricák akkor lettek helyesen felragasztva, ha az összes csúcsra ugyanaz a szám került. Hogyan ragaszthattuk fel a piros matricákat, ha az derül ki, hogy a zöld matricák felragasztására pontosan 6-féle helyes módszer van? Adjunk meg legalább egy megoldást!     3. Határozzuk meg azokat a lineáris $f\left(x\right)$, $g\left(x\right)$, $h\left(x\right)$ ($x\in \text{R}$) függvényeket, melyekre $\begin{array}{c}{\displaystyle F\left(x\right)=|f\left(x\right)|-|g\left(x\right)|+h\left(x\right)=\{{\displaystyle \begin{array}{cc}\hfill {\displaystyle -\mathrm{1,}}& {\displaystyle \text{ha }x<-\mathrm{1,}}\hfill \\ \hfill {\displaystyle 3x+\mathrm{2,}}& {\displaystyle \text{ha }-1\le x<\mathrm{0,}}\hfill \\ \hfill {\displaystyle -2x+\mathrm{2,}}& {\displaystyle \text{ha }0\le x\mathrm{.}}\hfill \end{array}}}\end{array}$     4. Tudjuk, hogy $n=2^{30}\cdot 3^{20}$. Hány olyan pozitív osztója van az $n^2$ számnak, mely kisebb $n$-nél és nem osztója $n$-nek?     5. Az $ABC$ egyenlő szárú háromszög derékszögű csúcsa $C$. Az $AC$ befogón felvesszük az $E$ és $F$ pontokat úgy, hogy $CE=FA$ teljesüljön! Legyen $Q$ pont a $C$ csúcsból a $BE$-re bocsátott merőleges talppontja, míg $R$ a $CQ$ egyenes és az $AB$ átfogó metszéspontja! Határozzuk meg, hogy a $CRF\sphericalangle$ felezője mekkora szöget zár be a $BC$ befogó egyenesével!     Harmadik (döntő) forduló       1. Egy 60 lapból álló kézirat oldalait rendre megszámozták az 1, 2, $\text{...}$, 120 oldalszámokkal. A kézirat néhány lapja azonban elveszett. A megmaradt lapok oldalaira írt számok összege 7159. Hány lap veszett el?     2. Az $ABC$ háromszög $BC$, $CA$, $AB$ oldalain adottak a $D$, $E$, $F$ pontok úgy, hogy az $AD$, $BE$, $CF$ szakaszok egy közös $O$ pontban metszik egymást. Határozzuk meg az $OF$ szakasz hosszát, ha $AO=23$, $BO=24$, $CO=29$, $OD=7$ és $OE=8$ egység hosszúságú!     3. Legyen $x$, $y$, $z$ három páronként különböző nem nulla valós szám! Határozzuk meg az $xyz$ szorzat értékét, ha tudjuk, hogy $\begin{array}{c}{\displaystyle x+\frac{1}{y}=y+\frac{1}{z}=z+\frac{1}{x}!}\end{array}$     II. kategória: Több, mint heti 3 órában matematikát tanuló (nem speciális tantervű) középiskolai tanulók       Első (iskolai) forduló     Megegyezik az I. kategória első fordulós feladatsorával.     Második forduló     Megegyezik az I. kategória második fordulós feladatsorával.     Harmadik (döntő) forduló       1. Hány olyan sorrendje van a 2007, 2008, 2009, 2010, 2011, 2012 és a 2013 számoknak, melyben bármely négy egymást követő szám összege osztható 3-mal?     2. Adott egy kör az $AB$ átmérőjével. Legyen $C$ a körvonal $A$-tól és $B$-től különböző pontja! Az $ABC$ háromszög $AB$ oldalán felvesszük a $D$ és $E$ pontot úgy, hogy $AD=AC$ és $BE=BC$ teljesüljön. Legyen $k_1$ a $BC$ befogót érintő $D$ középpontú, míg $k_2$ az $AC$ befogót érintő $E$ középpontú kör! Legyen $T$ az $ABC$ háromszög beírt körének, míg $T_1$ a $k_1$ és $T_2$ a $k_2$ körnek a területe! Hogyan vegyük fel a $C$ pontot, hogy a $\frac{T}{T_1+T_2}$ tört értéke maximális legyen? Mekkora ez a maximális érték?     3. Az $x$, $y$, $z$ egész számokra teljesül, hogy $x+y+z=2$. Tudjuk, hogy az $\begin{array}{c}{\displaystyle \frac{1}{xy+z-1}+\frac{1}{yz+x-1}+\frac{1}{zx+y-1}}\end{array}$ összeg egy prímszám reciprokával egyenlő. Melyik ez a prímszám?     III. kategória: Speciális tantervű osztályokban tanulók       Első (iskolai) forduló     Megegyezik az I. kategória második fordulós feladatsorával.   Második (döntő) forduló       1. Az $x$, $y$, $z$ egész számokra teljesül, hogy $x+y+z=2$. Tudjuk, hogy az $\begin{array}{c}{\displaystyle \frac{1}{xy+z-1}+\frac{1}{yz+x-1}+\frac{1}{zx+y-1}}\end{array}$ összeg egy prímszám reciprokával egyenlő. Melyik ez a prímszám?     2. Tekintsük azokat az emeletes hatványokat, melyek csupa 2-es számjegy felhasználásával alkothatók. (Tehát a következő számok szerepelhetnek bennük az egyes szinteken: 2, 22, 222, 2222, $\text{...}$, $\underset{k}{\overset{}{\underbrace{222\text{...}2}}}=B_k$.) Melyik a legnagyobb értékű ilyen emeletes hatvány, amely pontosan 2013 db 2-es számjegy felhasználásával képezhető?     3. Adott az $ABC$ tompaszögű háromszög. (A $C$-nél lévő szög nagyobb ${90}^{\circ }$-nál.) Bizonyítsuk be, hogy az $ABC$ háromszög feldarabolható 7 db hegyesszögű háromszögre.     HALADÓK I. kategória: Legfeljebb heti 3 órában matematikát tanuló középiskolai tanulók     Első (iskolai) forduló       1. Keressük meg az összes olyan egymás utáni egész számokból álló számötöst, ahol az első három szám négyzetének összege egyenlő az utolsó kettő szám négyzetének összegével!   2. 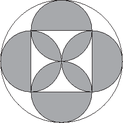Egy $2r$ sugarú körbe $r$ sugarú köröket rajzolunk az ábra szerint. Hanyadrésze a fehéren maradt területek összege a középen kialakuló négyzet területének?         3. Melyek azok az $N$ pozitív egész számok, amelyeknek prímtényezős felbontásában csak a 2 és a 3 hatványai szerepelnek, és $N$ összes osztójának a száma harmadrésze $N^2$ osztói számának?     4. Adott a síkon tíz pont, egy szabályos tízszög csúcsai. Hányféle módon választhatók ki ezen pontok közül egy olyan háromszög csúcsai, amely belsejében tartalmazza a tízszög középpontját?     5. Egy $k$-szor $n$-es sakktábla ($k>1$, $n>1$) mindegyik mezőjén áll egy figura. Egy adott jelre mindegyik figura egy, a saját mezőjével élben szomszédos valamelyik mezőre lép. Ha $k+n=2012$, akkor hány darab $\left(k;n\right)$ számpár esetén lehetséges, hogy a lépések után mindegyik mezőn legyen figura?     Második forduló       1. Milyen $a$, $b$, $c$, $d$ számjegyekre igaz, hogy $\left(\overline{ab}+\overline{cd}\right)\cdot 61=\overline{abcd}$?     2. Vegyünk fel az $ABCD$ téglalap belsejében egy $P$ pontot úgy, hogy $PB=4$, $PC=3$ és $PD=5$ legyen. Mekkora $PA$?     3. Legyen $a_n$ a következő módon definiált sorozat: $\begin{array}{c}{\displaystyle a_n=\{{\displaystyle \begin{array}{c}\hfill {\displaystyle a_1=\mathrm{18,}}\\ \hfill {\displaystyle a_2=\mathrm{48,}}\\ \hfill {\displaystyle a_n=a_{n-1}\cdot a_{n-2}\mathrm{,}}& {\displaystyle \text{ha }n>2.}\hfill \end{array}}}\end{array}$ Hány négyzetszám van a sorozat tagjai között?     4. Adott 50 szám, melyek összege 100. Bizonyítsuk be, hogy a számok közül kiválasztható 3 úgy, hogy az összegük legalább 6 legyen.     Harmadik (döntő) forduló       1. Határozzuk meg azokat a négyzetszámokat, amelyekre igaz, hogy ha felcseréljük két utolsó számjegyüket, továbbra is négyzetszámot kapunk!     2. Az $AFE$ hegyesszögű háromszög $ED$ és $FB$ magasságvonalai a $C$ pontban metszik egymást. Az $M$, $N$, $P$, $Q$ pontok rendre az $FC$, $EC$, $AE$, $AF$ szakaszok felezőpontjai. Bizonyítsuk be, hogy $MNPQ$ téglalap.     3. Az $x$, $y$, $z$ valós számokra $x+y+z=5$ és $xy+yz+zx=8$ teljesül. Igazoljuk, hogy $x$, $y$, $z$ bármelyikének értéke legalább 1, de legfeljebb $\frac{7}{3}$.     II. kategória: Több, mint heti 3 órában matematikát tanuló (nem speciális tantervű) középiskolai tanulók       Első (iskolai) forduló       1. A ,,23-as szám'' című misztikus filmben az egyik szereplő a házszámukat nagyon különlegesnek találja. A ház száma 1814, és az alábbi misztikus tulajdonságokat fedezi fel benne: (1) ha az első két számjegyhez hozzáadjuk a második kettőből képzett kétjegyű számot, akkor $1+8+14=23$-at kapunk; (2) ha az első két számjegyből képzett kétjegyű számhoz hozzáadjuk a másik két számjegyet, akkor $18+1+4=23$-at kapunk ismét; (3) ha a két kétjegyű számot adjuk össze, akkor $18+14=32$-őt kapunk, ami épp a 23 fordított sorrendben leírva. Tényleg különleges ebből a szempontból az 1814? Vagyis hány olyan négyjegyű szám van, amelyik rendelkezik a fenti három tulajdonság mindegyikével?     2. Határozzuk meg az $A$ szám pozitív egész osztóinak számát, ahol: $\begin{array}{c}{\displaystyle A=\sqrt[]{1+2011\cdot \sqrt[]{1+2012\cdot \sqrt[]{1+2013\cdot \sqrt[]{1+2014\cdot 2016}}}}\mathrm{.}}\end{array}$     3. Egy sík 20 darab egyenese összesen 187 darab metszéspontot határoz meg. Igazoljuk, hogy az egyenesek között vannak párhuzamosak.     4. Egy $t$ területű derékszögű trapézba az oldalakat érintő $r$ sugarú kör írható, ahol $t=\frac{25}{4}{r}^2$. Mekkora a trapéz alapjainak aránya?     5. Van 2012 darab számunk $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_{2011}\mathrm{,}{a}_{2012}$ mindegyik $\sqrt[]{2}+1$, vagy $\sqrt[]{2}-1$. Képezzük a következő összeget: $\begin{array}{c}{\displaystyle S=a_1{a}_2+a_3{a}_4+a_5{a}_6+\text{...}+a_{2011}{a}_{2012}\mathrm{.}}\end{array}$ Lehet-e $S=2012$?     Második forduló       1. Az $a$, $b$ pozitív egészek, és tudjuk, hogy $a^2+ab+b^2$ tízes számrendszerben felírva 0-ra végződik. Bizonyítsuk be, hogy legalább két nullára végződik.     2. Adott a síkon 6 pont, közülük semelyik három nincs egy egyenesen. Bizonyítsuk be, hogy található közöttük három, amelyek által meghatározott háromszögnek van egy legalább ${120}^{\circ }$-os szöge.     3. Nyolc darab pozitív egész szám összege és szorzata ugyanannyit ér. Mekkora ez a közös érték?     4. Egy konvex ötszög pontosan 100 darab egységnyi oldalú egybevágó szabályos háromszögből rakható ki (hézag- és átfedés nélkül). Mekkora lehet az ötszög kerülete?     Harmadik (döntő) forduló       1. Igazoljuk, hogy ha $n$ egész szám, akkor az $\frac{n^4+4n^2+3}{n^4+10n^2+16}$ tört nem egyszerűsíthető.     2. Egy négyzet tetszőleges belső pontja $P$, amin keresztül párhuzamosokat húzunk a négyzet oldalaival és átlóival. Ezek az egyenesek nyolc részre vágják a négyzetet. Bizonyítsuk be, hogy a keletkezett részek két olyan csoportba oszthatók, amelyekben a részek területének összege egyenlő.     3. Egy $n$ sorból, és 7 oszlopból álló ($n\times 7$-es) táblázatot szeretnék kitölteni a következő módon: ‐ Minden sorban az 1, 2, 3, 4, 5, 6, 7 számok kell, hogy szerepeljenek valamilyen sorrendben (természetesen a sor valamennyi mezőjébe pontosan egy szám kerül). ‐ Bármely két sornak legalább egy helyen/egy mezőben különböznie kell. ‐ Bármely két sor legalább egy helyen meg kell egyezzen. Legfeljebb mennyi lehet $n$?     III. kategória: Speciális tantervű osztályokban tanulók       Első (iskolai) forduló       1. Egy kör kerületére felírjuk 1-től 13-ig az egészeket valamilyen sorrendben. Három (a kör mentén) szomszédos számot triónak nevezünk. (13 ilyen csoport van.) A trióban lévő három szám összegét: a trió összegének hívjuk. Egy trió maximális, ha a trió összege nagyobb, vagy egyenlő, mint az adott sorrendnél fellépő másik 12 trió bármelyikének az összege. Mennyi a maximális trió összegének minimuma (az összes lehetséges sorrend esetén)?     2. Egy konvex ötszög pontosan 100 darab egységnyi oldalú egybevágó szabályos háromszögből rakható ki (hézag- és átfedés nélkül). Mekkora lehet az ötszög kerülete?     3. Van 15 darab különböző 2 és 2013 közé eső pozitív egészünk úgy, hogy bármely kettő (különböző) közülük relatív prím egymáshoz. Igazoljuk, hogy a számok között van prím!     4. Az $ABCD$ négyzet $BD$ átlóján úgy vettük fel az $M$ és $N$ pontokat, hogy $\begin{array}{c}{\displaystyle B{M}^2+N{D}^2=M{N}^2\mathrm{.}}\end{array}$ Mekkora az $MAN\sphericalangle$?     5. Melyek azok az $x$ valós számok, amelyekre teljesül, hogy $\begin{array}{c}{\displaystyle \left[x\right]+\left[2x\right]+\left[3x\right]+\text{...}+\left[2012x\right]=2013?}\end{array}$ ($\left[y\right]$ értéke az a legnagyobb egész szám, amely $y$-nál nem nagyobb.)     Második (döntő) forduló       1. Az $ABC$ háromszög beírt köre az $AC$ és $BC$ oldalakat az $X$ és $Y$ pontokban érinti. A $B$-ből induló belső szögfelező az $XY$ szakaszt $P$-ben metszi. Mekkora az $APB\sphericalangle$?     2. 2013 valós számra fennáll: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle a_1\ge a_2\ge a_3\ge \text{...}\ge a_{2012}\ge a_{2013}\ge \mathrm{0,}\text{valamint}}\hfill \\ \hfill {\displaystyle }& {\displaystyle a_{34}^2+a_{35}^2+\text{...}+a_{2013}^2\ge \frac{61}{4}\mathrm{.}}\hfill \end{array}}$ Igazoljuk, hogy $a_1+a_2+a_3+\text{...}+a_{2012}+a_{2013}\ge \sqrt[]{2013}$! Lehet-e a fenti 2013 tagú összeg pontosan $\sqrt[]{2013}$?     3. Artúr király udvarába hivatalos vendégségbe néhány lovag. Bármely két lovag vagy barát, vagy ellenség (a viszonyok kölcsönösek, és az idő múlásával nem változnak). Egy korábbi vendégség során ugyanezek a lovagok le tudtak ülni két asztal mellé úgy, hogy az egy asztalnál ülők mind barátai voltak egymásnak. A mostani vendégség során a vendégek egyesével érkeztek meg. Érkezésük után minden érkező leült az egyik olyan asztalhoz, ahol nem ült ellensége; az ilyen asztalok közül azt választva, ahol a legtöbb barátja ült (ha egyetlen megfelelő asztal sem volt, akkor az érkező természetesen új asztalhoz ült). Így összesen 12 asztal mellé ültek le lovagok. Legalább hány lovag érkezett a vendégségbe?