Kezdőlap


Cím:	53. Rátz László Vándorgyűlés Békéscsabán
Szerző(k):	Marczis György
Füzet:	2013/október, 407 - 411. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A Bolyai János Matematikai Társulat a Szent István Egyetem Gazdasági, Agrár- és Egészségtudományi Karral, az Andrássy Gyula Gimnázium és Kollégiummal, valamint a BJMT Békés Megyei Tagozatával, mint társrendezőkkel július 2‐5-ig szervezte meg az 53. Rátz László Vándorgyűlést, a matematikatanárok éves konferenciáját. A Kárpát-medencéből közel 200 pedagógus volt Békéscsaba vendége.
Akik korábban érkeztek, kedden délelőtt egy békéscsabai, városnéző sétán vehettek részt. A megnyitó július 2-án (kedden) 14 órakor volt az egyetem nagyelőadójában. A vendégeket előbb Kiss Tibor, Békéscsaba Megyei Jogú Város alpolgármestere, majd a házigazdák részéről Molnár István intézetigazgató köszöntötte. Utána a Beke Manó-emlékdíjak átadása következett. A kitüntetések átadása után a Mütyür Banda (felkészítő Barbócz Sándor), egy kisiskolásokból álló négytagú népi zenekar bűvölte el játékával a résztvevőket. Őket Lajos Józsefné és Pálfalvi Józsefné Óriások vállán $...$ című előadása követte, majd Róka Sándor, Rátz Tanár Úr Életműdíjas számolt be az elmúlt 30 év élményeiről.
A négynapos program alatt 37 előadás volt az általános iskolai alsó és felső tagozatos valamint a középiskolás szekcióban. Az előadók között volt Sipos Imre, közoktatásért felelős helyettes államtitkár is, aki közoktatásunk aktuális kérdéseiről beszélt.
Népszerű volt a tanárok tesztversenye is, amelyen a vállalkozó kedvűek megmérhették tudásukat a nem könnyű feladatsorokon.
Nem maradtak el a hagyományos kirándulások sem. Az egyik csoport Aradra ment. A város nevezetességeinek megtekintése után egy borkóstolós vacsorán vettek részt Ópáloson. A többi kiránduló Békés megye kastélyaival és kúriáival ismerkedhetett meg. Ők egy hangulatos gyulai vacsorával zárták a napot.
A legmozgékonyabbak focizhattak, kosarazhattak is.
A vándorgyűlés minden szempontból sikeres volt: a magas színvonalú előadásoknak a Szent István Egyetem kifogástalan helyszíne volt, a szállás és az ellátás is minden igényt kielégített, a szervezők is mindent megtettek a program sikeréért, állapította meg az Oktatási Bizottság záró, értékelő és tervező ülésén.
A részletes programot, az előadások anyagát megtalálhatják a www.bolyai.hu és a www.rlv.berzsenyi.hu honlapokon.

\begin{matrix} Marczis GyörgyBJMT Békés Megyei Tagozata \end{matrix}

A középiskolás tanárverseny feladatai

A verseny időtartama 90 perc. A feladatok pontozása: minden helyes válasz 5 pontot ér; helytelen válaszra 0 pont jár; válasz nélkül hagyott kérdésekre 1-1 pontot adunk. A versenyen íróeszközön, papíron, körzőn és vonalzón kívül semmilyen más segédeszköz nem használható. A verseny támogatói a MATEGYE Alapítvány, a Maxim Kiadó és a Typotex Kiadó.
1. Nekeresd város térképén minden teret kör és minden utcát szakasz jelöl (lásd ábra). Legkevesebb hány téren kell kamerát felszerelni ahhoz, hogy a kamerákkal az összes tér látható legyen? (Kamerával azon a téren kívül, ahova felszerelték, azok a terek láthatók, amelyeket a kamerával felszerelt térrel utca köt össze.) (A) 1; (B) 2; (C) 3; (D) 4; (E) 5.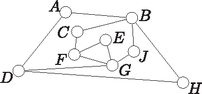

2. Hány fok az

\vec{a} (5 - \sqrt[]{3}; - 11)

és

\vec{b} (5 + \sqrt[]{3}; 2)

vektorok által bezárt szög? (A) 25; (B) 30; (C) 45; (D) 60; (E) 90.
3. Hány különböző pozitív egész értéket vehet fel

n

, ha az 1; 3; 7; 2; 6; 3 és

n

statisztikai minta minden eleme egész szám, mediánja 3 és terjedelme legfeljebb 10? (A) 9; (B) 10; (C) 11; (D) 12; (E) 13.
4. Melyik összefüggés igaz az

A = (\frac{1}{5^{x}} + \frac{1}{5^{y}}) \cdot 5^{x + y}

szorzatra tetszőleges

x

y

természetes szám esetén? (A)

\frac{1}{5} \leq A < \frac{2}{5}

; (B)

\frac{2}{5} \leq A < 1

; (C)

1 \leq A < 2

; (D)

A \geq 2

; (E) az előzőek közül egyik sem.
5. Egy természetes számot púposnak nevezünk, ha bármely két szomszédos számjegye különböző, és a számjegyei balról jobbra haladva a számban szereplő legnagyobb számjegyig növekednek, majd ettől a számjegytől kezdve csökkennek. Hány 18-jegyű púpos szám van? (A) 0; (B) 1; (C) 2; (D) 3; (E) 4.
6. Milyen ponthalmazt határoznak meg a Descartes-féle derékszögű koordináta-rendszerben azok a

P (x; y)

pontok, melyek koordinátáira az

x^{2} y^{2} - 2 y^{3} - 4 x^{2} + 8 y = 0

egyenlet teljesül? (A) Négy egyenest; (B) egy kört és két egyenest; (C) két egyenest és egy parabolát; (D) két parabolát; (E) az előzőek közül egyik sem.
7. Ági felírta az összes háromjegyű pozitív egész számot egy-egy papírlapra (mindegyikre csak egy számot írt, és egyik számot sem írta egynél több lapra), majd ezeket beletette egy dobozba. Legkevesebb hány lapot kell kihúznia közülük becsukott szemmel, hogy a kihúzott lapokon szereplő számok között biztosan legyen két olyan, amelyeknek az összege osztható hárommal? (Ági a kihúzott papírlapokat nem teszi vissza a dobozba.) (A) 3; (B) 4; (C) 301; (D) 302; (E) 602.
8. Mennyi az

(x - \frac{1}{x})^{5}

értéke, ha

x^{2} + x - 1 = 0

? (A)

- 2

; (B)

- 1

; (C) 0; (D) 1; (E) 2.
9. Zsuzsi és Andris a parkban fogócskázik. (A park térképét a mellékelt ábra mutatja. Az ábrán a körlapok bokrokat, a vonalak a bokrok közötti lehetséges futási útvonalakat jelölik.) A fogócska kezdetén Andris az 1-es, Zsuzsi a 2-es bokornál áll. Andris el akarja fogni Zsuzsit. Ez akkor sikerül, ha Andris ahhoz a bokorhoz tud futni, ahol akkor éppen Zsuzsi van. A gyerekek felváltva mozognak úgy, hogy mindig a vonalak mentén futnak át egy közvetlenül szomszédos bokorhoz. Egy ilyen futást egy lépésnek nevezünk. Az első lépést Andris teszi meg. Leghamarabb Andris hányadik lépésénél sikerül elfognia Zsuzsit, ha mindketten a legügyesebben játszanak? (A) 4. (B) 5. (C) 6. (D) 10. (E) Andrisnak nem sikerül elfogni Zsuzsit.

10. Egy távoli bolygóról egyfejű és kétfejű űrlények érkeztek a Földre. Az egyfejűek mindegyikének 1 feje, 5 keze és 3 lába, a kétfejűek mindegyikének 2 feje, 6 keze és 4 lába van. Hány lábuk van összesen a Földre érkezett űrlényeknek, ha kezeik és fejeik számának az összege 100? (A) 20; (B) 50; (C) 100; (D) 200; (E) ezekből az adatokból nem lehet meghatározni.
11. Egy 1-től 6-ig számozott dobókockával háromszor dobtunk. A dobott számokból egy kétjegyű és egy egyjegyű számot készítettünk, majd összeszoroztuk ezt a két számot. Melyik számot kaphattuk meg szorzatként az alábbiak közül? (A) 38; (B) 85; (C) 260; (D) 335; (E) 398.
12. Ottó most kétszer annyi idős, mint amennyi Anna akkor lesz, amikor Emma annyi idős lesz, mint amennyi Ottó most. Melyik összefüggés igaz, ha a gyerekek életkorát nevük kezdőbetűje jelöli? (A)

A< E< O

; (B)

A< O< E

; (C)

E< A< O

; (D)

E< O< A

; (E)

O< A< E

.
13. Az ábrán látható gráf

A

pontjából a

B

pontjába úton szeretnénk eljutni. Mennyi a valószínűsége az

A E C D B

út választásának, ha a gráf minden pontjára igaz, hogy onnan a lehetséges következő éleken való haladás valószínűségei egyenlők? (A)

\frac{8}{27}

; (B)

\frac{1}{8}

; (C)

\frac{1}{6}

; (D)

\frac{1}{5}

; (E)

\frac{1}{2}

14. Tekintsük a valós számokon értelmezett valós értékű

f

függvényt, amelyre bármely valós

x

y

számpár esetén

f (x \cdot y) = f (x) + f (y)

teljesül! Mennyi az

f (2013)

? (A) 0; (B) 1; (C) 2; (D) 2013; (E) az előzőek közül egyik sem.
15. Hány megoldása van a

\sqrt[2 cos x]{4} = 8^{\frac{1}{3} + sin x}

egyenletnek a

[0; 2013 π]

intervallumon? (A) 1006; (B) 1007; (C) 2012; (D) 2013; (E) 3019.
16. Egy szöcske az ábrán kívülről ráugrott az 1 számot tartalmazó négyzetre. Innen tovább ugrált úgy, hogy minden ugrásával egy szomszédos négyzetre ugrott át. (Két négyzet szomszédos, ha van közös oldaluk.) Végül a szöcske a csillaggal jelölt négyzetről ugrott le az ábráról. Hányszor ugrott a szöcske a csillaggal jelölt négyzetre, ha a négyzetekbe írt számok azt jelölik, hogy a szöcske hányszor ugrott arra a négyzetre? (A) 7; (B) 8; (C) 13; (D) 15; (E) 16.

17. Hány olyan

b

egész szám van, amelyre a

b - 2

különbség osztója a

b^{3} - 2

különbségnek? (A) 2; (B) 4; (C) 6; (D) 8; (E) végtelen sok.
18. Mennyi az

[log_{n + 1} n + log_{n} (n + 1)]

, ha az

n

1-nél nagyobb természetes szám? (Az

[a]

jelenti az

a

szám egész részét.) (A) 0; (B) 1; (C) 2; (D) 3; (E) az érték

n

-től függ.
19. Anna, Berci és Csaba olyan kártyával játszanak, amelyben 5 fehér színű (az egyik oldalán 1-től 5-ig sorszámozott) és 5 fekete színű (az egyik oldalán szintén 1-től 5-ig sorszámozott) lap van. A játék kezdetén mind a három játékos maga elé rakta a saját lapjait számmal lefelé vagy felfelé fordítva úgy, hogy bármelyik két lapja közül a jobb oldalin legalább akkora szám volt, mint a másikon (lásd ábra). Mennyi a legtöbb olyan lap a számmal lefelé fordított 9 lap közül, amelyről megállapítható, hogy melyik szám van rajta? (A) 1; (B) 6; (C) 7; (D) 8; (E) 9.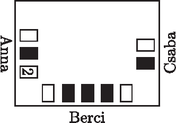

20. Egy kupacban kavicsok vannak. Köves Péter és Kavicsos Pál felváltva vesznek a kupacból legalább 1 és legfeljebb 10 kavicsot. Amikor már az összes kavicsot elvették a kupacból, megszámolják hány kavics van náluk. Ha a kapott két szám relatív prím, akkor Péter nyer; ha nem, akkor Pál. Hány kavics esetén fog mindig Péter győzni az alábbiak közül, akárhogyan is választja a kavicsokat? (A) 247; (B) 323; (C) 437; (D) 1001; (E) 1019.
21. Mennyi a

log_{4} (1 + a^{2}) + log_{4} (1 + b^{2})

összeg maximuma, ha

a^{2} + b^{2} = 2

és

a, b \in R

? (A) 1; (B) 2; (C)

\frac{5}{2}

; (D) 3; (E)

\frac{7}{2}

.
22. Hány olyan

(p; q; r)

számhármas van, amelynek az elemei különböző prímszámok és

p^{2} + q^{2} = r^{2}

? (A) 0; (B) 1; (C) 2; (D) 3; (E) 4.
23. A majmoknál minden fontos kérdésben a 3 fős Bölcsek Tanácsa dönt. A Tanács a döntéseit egyszerű szótöbbséggel hozza meg. (Az egyszerű szótöbbség azt jelenti, hogy azt fogadják el, amelyikre többen szavaztak.) A Bölcsek Tanácsának mindig a 3 legokosabb majom a tagja, ennek ellenére a Tanács minden tagja a döntések 10%-ában hibás döntést hoz. Az összes döntések hány százalékában hoz hibás döntést a Bölcsek Tanácsa? (A) 0,1; (B) 2,8; (C) 10; (D) 27,1; (E) 30.
24. Mennyi az

x^{2} + \frac{1}{x^{2}}

összeg, ha

x^{3} + \frac{1}{x^{3}} = 18

? (A) 6; (B) 7; (C) 8; (D) 9; (E) 10.
25. Egy

8 \times 8

-as pontrács mind a 64 rácspontját kékre vagy pirosra színeztük úgy, hogy a négy sarokban lévő pont piros színű lett. (Egy rácspont sarokban van, ha szélső sorra és szélső oszlopra illeszkedik.) A színezés után a pontok között 16 volt kék színű, ezek közül 8 a pontrács valamelyik szélső sorában vagy szélső oszlopában helyezkedett el. Először egy-egy szakasszal összekötöttük az azonos sorban lévő szomszédos pontokat, majd az azonos oszlopban lévő szomszédos pontokat úgy, hogy az azonos színű pontokat velük egyező színű, a különböző színű pontokat fekete színű szakasszal kötöttük össze. Hány fekete színű szakaszt rajzoltunk, ha a piros színű szakaszok száma 69 lett? (A) 22; (B) 24; (C) 26; (D) 30; (E) 43.
26. Milyen intervallumból veszi fel

z

az értékeit, ha

x + y + z = 5

és

x y + y z + z x = 3

, ahol

x

y

és

z

valós számok? (A)

[- 3; - \frac{7}{3}]

;

(B)

] - \frac{7}{3}; - \frac{5}{3}]

; (C)

] - \frac{5}{3}; - 1 [

; (D)

[- 1; \frac{13}{3}]

; (E)

] \frac{13}{3}; 5]

.
27. Az

A B C

háromszög belsejében úgy helyezkedik el a

P

pont, hogy

C A P ∢ = 10^{\circ}

P C A ∢ = 20^{\circ}

P A B ∢ = 30^{\circ}

és

A B C ∢ = 40^{\circ}

. Hány fok a

C P B

szög? (A) 65; (B) 70; (C) 75; (D) 80; (E) 90.
28. A testnevelésóra elején András, Béla, Csaba, Dénes, Elemér és Ferenc ebben a sorrendben állt egymás mögött. Az óra végén a hat fiú úgy állt egymás mögé, hogy az első helyre kerülő fiú kivételével mindegyik fiú elé került legalább egy olyan fiú, aki az óra elején szomszédja volt. Hányféle sorrendben állhatott egymás mögött az óra végén a hat fiú? (A) 15; (B) 24; (C) 32; (D) 45; (E) 120.
29. Egy konvex négyszög területe 32 cm

^{2}

, egyik átlója hosszának és két egymással szemközti oldala hosszának összege 16 cm. Hány centiméter a négyszög másik átlójának a hossza? (A)

6 \cdot \sqrt[]{2}

; (B)

6 \cdot \sqrt[]{3}

; (C) 8; (D)

8 \cdot \sqrt[]{2}

; (E)

8 \cdot \sqrt[]{3}

.
30. Egy körvonalon véletlenszerűen kijelölünk három különböző pontot,

P

-t,

Q

-t és

R

-t. Mennyi a valószínűsége annak, hogy az így kapott

P Q R

háromszög hegyesszögű? (A)

\frac{1}{5}

; (B)

\frac{2}{9}

; (C)

\frac{1}{4}

; (D)

\frac{3}{10}

; (E)

\frac{2}{5}

\begin{matrix} A feladatsortCsordásné Szécsi Jolánállította össze \end{matrix}

A középiskolás tanárverseny eredménye

1. Fonyó Lajos (Keszthely, Vajda János Gimn.),
Molnár István (Békéscsaba) ..... 116 pont
3. Cs. Nagy András (Vác, Boronkay György MKI) ..... 115 pont
4. Fridrik Richárd (Szeged, SZTE hallgató) ..... 114 pont
5. Eckert Bernadett (Szeged, Radnóti Miklós Kísérleti Gimn.) ..... 112 pont
6. Kiss Géza (Fazekas M. Főv. Gyak. Gimn.) ..... 110 pont
7. Róka Sándor (Nyíregyháza) ..... 108 pont
8. Baloghné Cseh Judit (Szolnok, Varga Katalin Gimn.) ..... 105 pont
9. Bertalan Zoltán (Békéscsabai Gépészeti és Számítástechnikai Szki.) ..... 103 pont
10. Kovács Béla (Szatmárnémeti, Hám János Teológiai Líceum) ..... 100 pont.

Az általános iskolás tanárverseny¹ eredménye

1. Nagy Tibor (Kecskemét, Kecskeméti Református Ált. Isk.) ..... 141 pont
2. Tóth Gabriella (Palics, Miroslav Antić Ált. Isk.) ..... 132 pont
3. B. Varga József,
Egyed László (Baja, III. Béla Gimn.) ..... 130 pont.

¹Az általános iskolás tanárverseny feladatait nem közöljük.